租房多属性决策支持系统的设计

霍子明

（中央财经大学会计学院 北京市 100081）

1 引言

互联网的出现和普及给租房者带来了极大的便利，各式各样的租房平台层出不穷，链家、贝壳是在租房市场中占据了较大份额的两家公司。它们主要向用户提供的是租房信息的垂直搜索功能，不仅向用户提供基本的关键词搜索,还结合房子的一些特征信息，如位置、面积、价格、户型等作为筛选条件供用户选择，满足了用户的一部分需求。另外，这些公司越来越重视地图与搜索功能的交互结合,进而实现地图可视化搜索。但这些租房平台主要提供的还是以租房地点为中心，距离、面积、价格等特征值为导向的搜索，而并不能帮助用户决策。这样的搜索不仅使得找房过程更加繁琐，还无法满足用户对于房源的多元化、个性化需求。

租房者进行选房决策时，很难根据简单的信息搜索就选出合适的房源，其本身的习惯、偏好也会在选房过程中起到相当重要的作用。TOPSIS 法是一种经典常用的多属性决策方法，被广泛的应用于选址、供应商选择等问题。因此,分析传统TOPSIS 法缺陷和不足，设计一种适用于租房推荐领域的TOPSIS 模型、开发出一套基于该模型的租房决策支持系统是一个十分具有意义的研究方向。

2 决策模型设计

租房多属性决策是指租房者根据自身的偏好，在考虑出租房源的特性的基础上，采用某种决策准则对有限个出租房源进行排序，进而选择出合适的房源[1]。在租房多属性决策大致分为三个步骤：

（1）确定租房决策矩阵；

（2）确定房源属性权重；

（3）进行租房综合评价。

其中确定租房决策矩阵是要确定选择哪些指标对出租房源进行衡量，并且要考虑使用哪些变量来衡量这些指标。确定房源属性权重就是确定选择何种方法来确定权重能有效反映出租房者在租房过程中的不同偏好；进行租房综合评价就是使用特定的算法或模型对出租房屋进行排序，选择出适合租房者的。

表1：房源指标变量

表2：三种赋权方法对比

表3：重要性判断尺度

2.1 确定租房决策矩阵

确定决策矩阵首先确定租房过程中哪些指标对租房者是重要的，仔细考虑不同年龄阶段、不同需求的租房者在租房选房时的标准。本文拟设置上班距离、最近地铁站距离、生活便利程度，教育水平指标、医疗资源指标，绿化环境指标、租房价格指标、价格合理指标八个指标，同时考虑使用相应的变量来衡量这些指标，具体见表1。

2.2 确定房源属性权重

在租房多属性决策问题中，属性的权重起到十分重要的作用，它可以用来衡量某一个属性的相对重要程度，进而反应租房者的偏好。不同的权重组合反映了租房者的不同需求，租房者认为一个属性越重要，则应该赋予它的权重就越大，反之就越小。

目前，针对确定权重的方法的研究很多，但大致可以将这些方法分为三种：第一种为主观赋权法，它根据决策者主观上对各个属性的重要性的判断来确定权值，权重来自于决策者的经验。常用的主观赋权法有层次分析法（AHP 法）以及专家调查法（德尔菲法）等。第二种为客观赋权法，该方法基于决策矩阵中的属性值之间的关联关系或者是它们的分散程度来确定每个属性所对应的权值，不依赖于决策者的经验，常用的方法有：主成分分析法、因子分析法、熵值法等。运用主观赋权法确定权重，权重来自于决策者的经验，其过程会有很大的随意性，经验丰富的决策者可能可以确定出合适的权重，但新手决策者可能就无从下手。而客观赋权法虽然有数据做支撑，但得到的权值常常不具有客观的意义，还可能忽略决策者的主观信息。由于上述两种赋权方法各有优劣，决策者们又提出了第三种组合赋权法。该方法将属性值反映出的信息以及决策者本身的主观信息相结合，使用该方法得到的权重，既能反应数据的特征又可以反映决策者的经验，但有时使用组合赋权法的过程过于复杂，结果有时可能不如使用单一赋权法准确。组合赋权法主要有熵权法与层次分析法相结合，熵权修正G1 法等等。表2 为主观赋权法、客观赋权法与组合赋权法三种方法的对比。

考虑到不同需求决策者的主观意愿相差较大，为了准确的满足租房者的不同需求，本文拟采用熵权法与层次分析法相结合来确定每一位使用系统的租房者的组合权值，在符合数据客观规律的同时又可以满足租房者个性化需求。

2.2.1 层次分析法

层次分析法由Saaty 于1970年提出，是一种定性与定量相结合的、系统化层次化的主观赋权方法。本文使用层次分析法确定权重的步骤如下[2]：

（1）建立层次结构模型。分为目标层，准则层，方案层，如图1。

（2）构建判断矩阵。判断矩阵是租房者对准则层的n 个评价指标的重要程度的比较，在本文中，有8 个评价指标的情况下，判断矩阵为8 阶方阵。

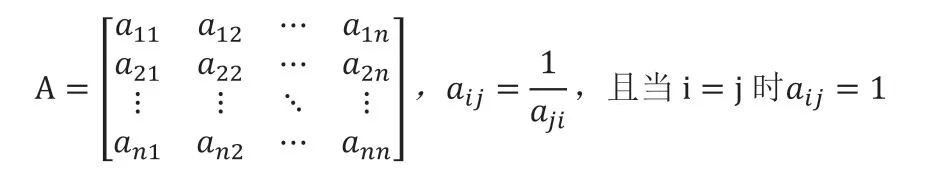
比较第i 个指标与第j 个指标相对的重要性时，使用数量化的相对权重aij来衡量。aij的值由租房者根据主观意愿所决定，遵循表3 中的规则：

例如a21=3 表明租房者认为第二个指标对于第一个指标来说比较重要，a31=1/3 表明租房者认为第一个指标对于第三个指标来说比较重要。

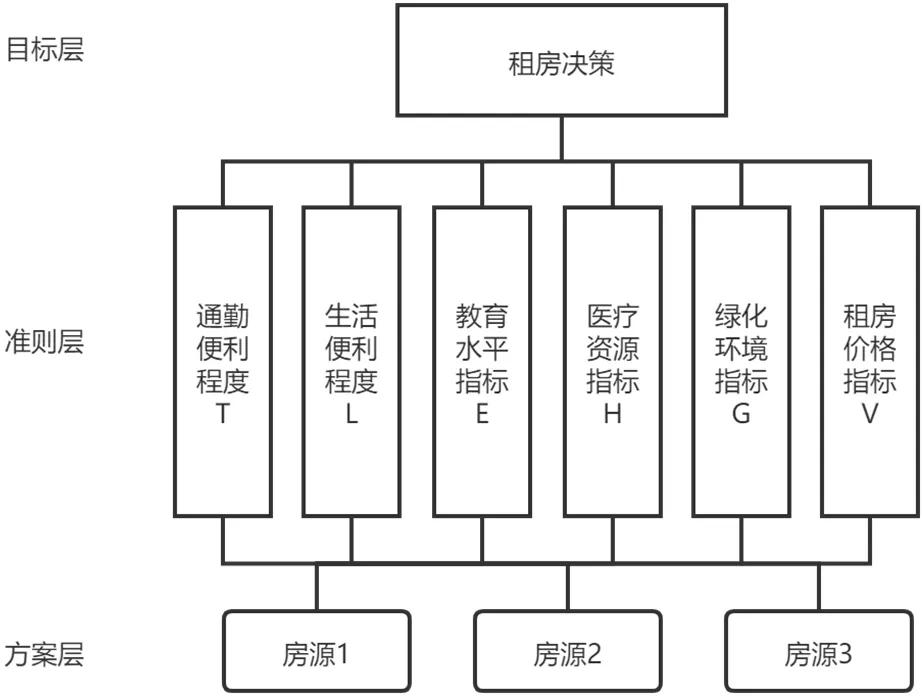
图1：租房决策层次结构模型

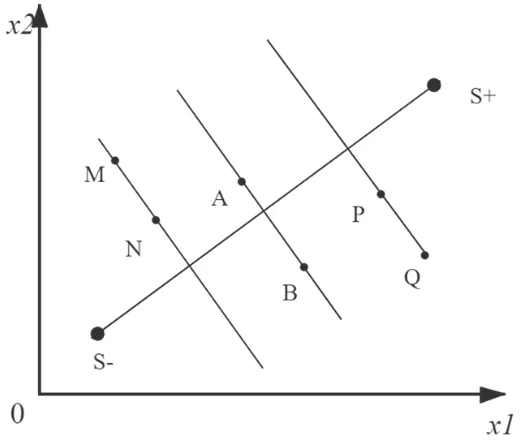
图2

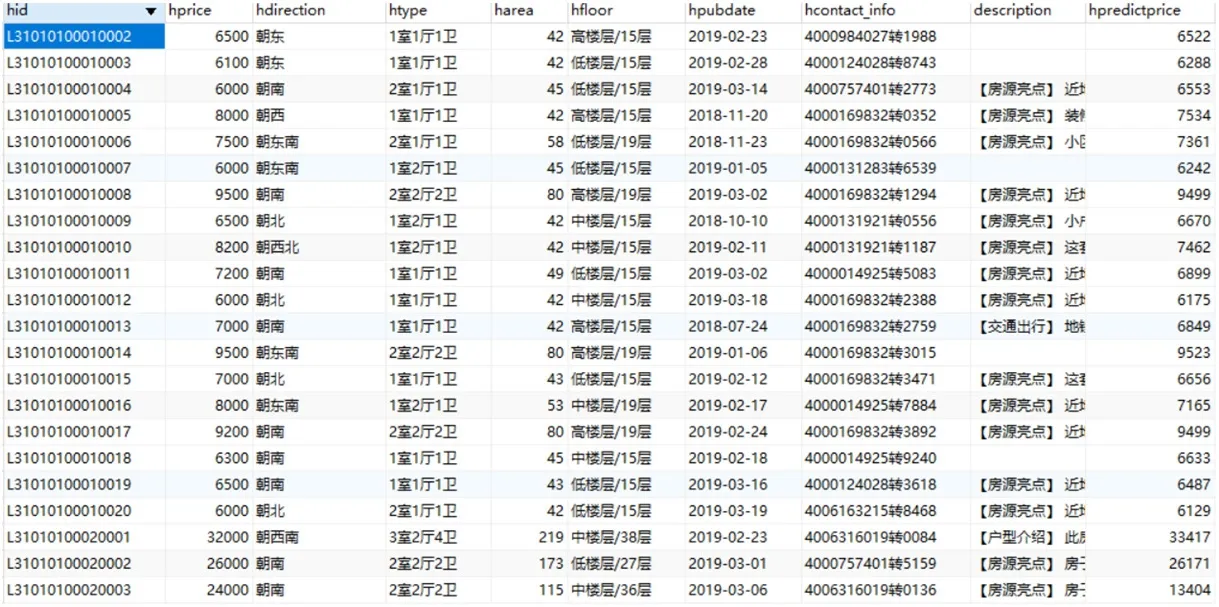
图3：原始房源数据

（3）计算权重向量。采用算数平均数法计算权重，即：

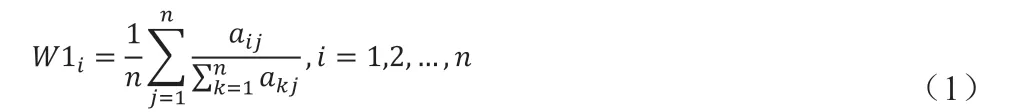
具体步骤为：①将判断矩阵A 中的每一个元素按列归一化，即②将归一化后的各列相加；③将相加后的向量除以n 即得到权值向量；

（4）进行一致性判断。

①计算一致性指标CI（consistencyindex）

其中，CI 越小，说明A 越接近一致矩阵；

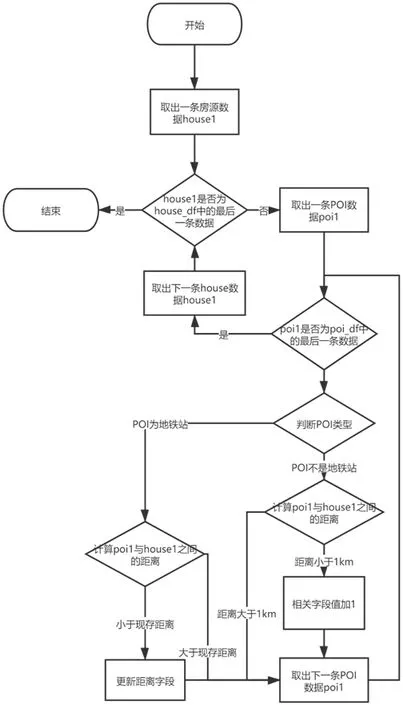
图4：计算房源周围商家算法

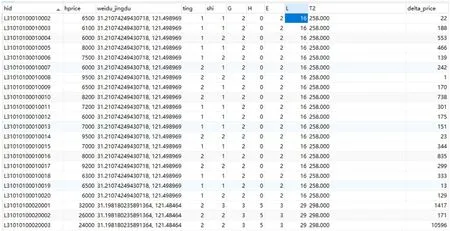
图5：处理后的房源数据

②根据RI 指标表（表4）计算一致性比例CR（consistencyratio）

如果CR＜0.1，则认为矩阵有较强的一致性，否则需要对矩阵进行调整。

2.2.2 熵权法

在利用熵权法评估某一指标时，若该指标的信息量越大，则不确定性越小，熵值对应的也越小；反之如果该指标的信息量越小，则不确定性越大，熵值对应也越大。由上述分析可以得出，熵值越小的指标提供的信息量越大，越为集中，故其权值也越大；熵值越大的指标提供的信息量越少，越为混乱，故其权也越小。因此，可以利用各指标的不确定性计算出熵值，进而求出对应的熵权值。具体的步骤如下[3]：

（1）计算熵值。

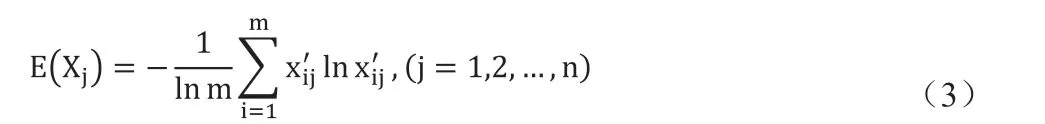
（2）计算各指标的熵权值。

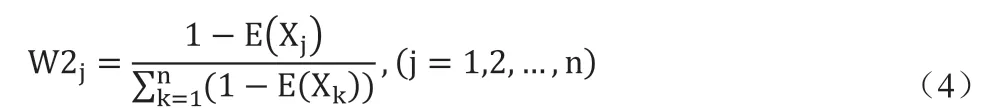
熵权值W2j越大，则说明该指标所提供的信息量越大，表示其对综合评价的作用也越大。

根据层次分析法所得到的权值W1 以及熵权法所得到的权值W2 形成组合权值W。

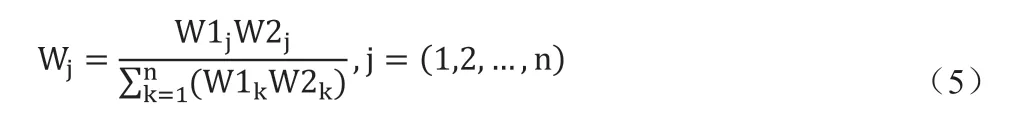
2.3 租房综合评价

TOPSIS 法的全称为逼近理想解排序方法（Technique for order performance by similarity to ideal solution），是由C.L.Hwang和K.Yoon在1982年提出的一种多属性决策方法，该方法按照各个方案到正理想解和负理想解的接近程度对有限个目标进行相对优劣排序。其中，正理想解是决策者设想出的最合适的方案，它的每一个单个属性值都达到了备选方案中的最优值；而负理想解则是决策者设想出的最不合适的方案，它表示单个属性值都达到了备选方案中的最差值。TOPSIS 法的核心就是通过计算备选方案到正、负理想解的欧式距离来进行相对优劣的排序，如果一个待选方案距离正理想解最近而距离负理想解最远，那么这个方案就是我们要寻找的最优方案。使用TOPSIS 法进行综合评价的具体步骤如下[4]：

Step1：构建样本数据的评价矩阵

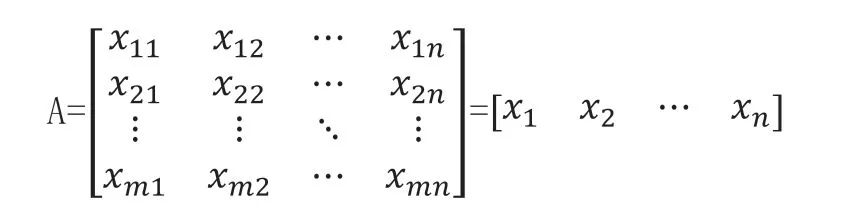
该矩阵表示共有m 个评价对象，n 个属性指标，其中xij表示第i（i=1,2,…,m）个评价对象的第j（j=1,2,…,n）个属性指标所对应的原始属性值。

Step2：由于不同指标之间量纲和数量级都不同，故需要对矩阵A 进行规范化处理，使其中属性可以放在一起比较。数据规范化的方法很多，这里使用常用的向量规范化：

对于效益型指标：

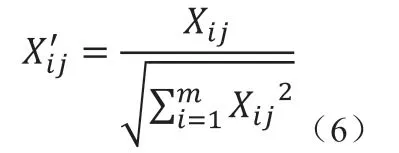
对于成本型指标：

其中M 为每一列的最大值

由此得到了归一化的评价矩阵：

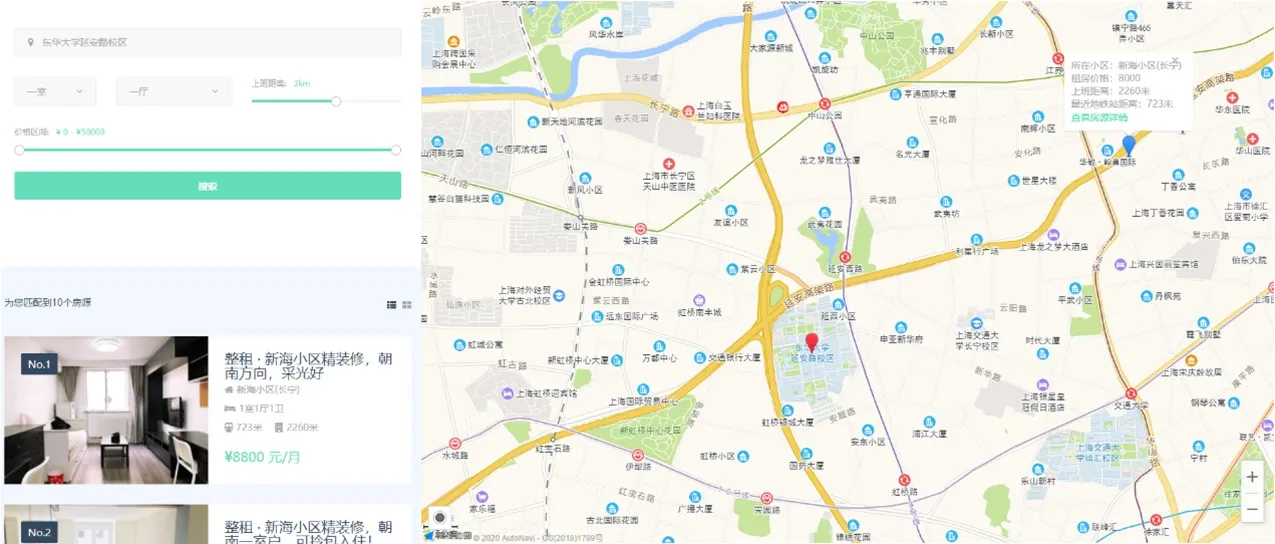
图6：在线决策页面

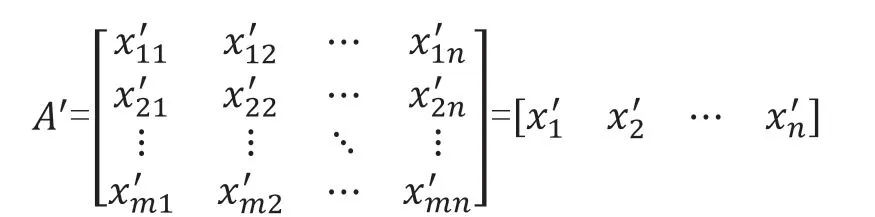
Step3：将权重矩阵W=(w1w2…wn)右乘规范化后的评价矩阵A'得到价值矩阵V

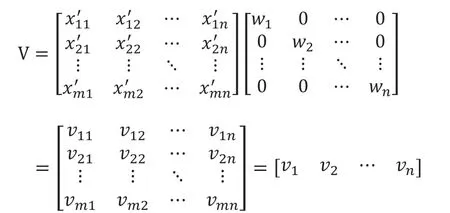
其中，Wi=(0,…,0,wi,0,…,0)T,权值满足。

Step4：确定正理想解S+与负理想解S-，即

Step5：分别计算第i 个备选方案到正理想解S+的距离以及到负理想解的S-距离即

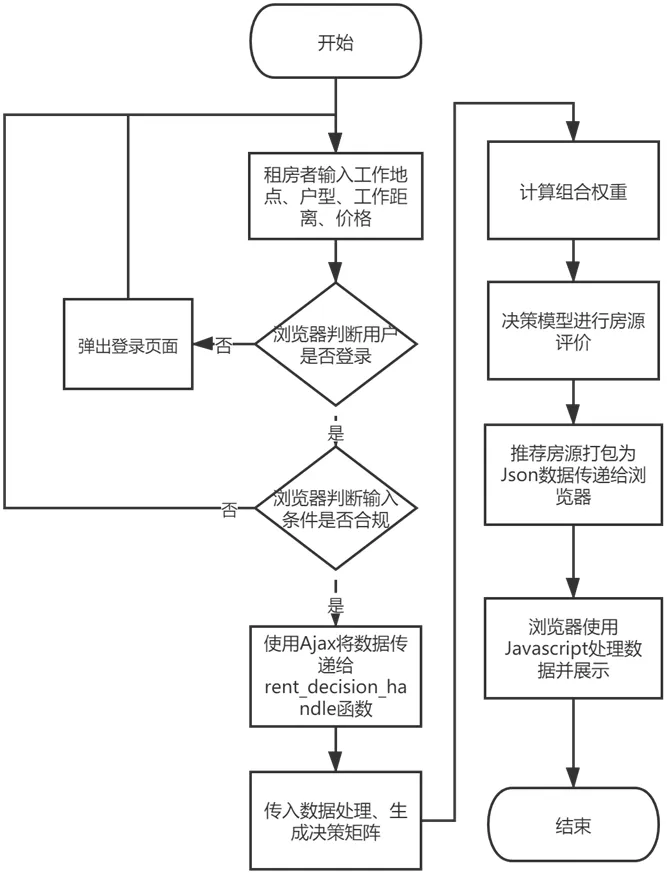
图7：在线决策模型计算流程图

Step6：计算各方案的相对贴近度

Step7：根据Ci的大小对各评价对象进行排序，显然Ci∈[0,1]，Ci值越大，代表评价对象越好。

将TOPSIS 法应用于租房领域中要注意一些特殊的房源所导致的排序结果不准确的问题[5]。为了解释这个问题，不妨假设x1，x2为出租房源的两个属性，如图2所示，点S-对应负理想解向量，点S+对应正理想解向量，其他点M,N,P,Q,A,B 为六个出租房源所对应的点。MN 是S-S+中垂线左下方的一条垂线，P，Q 则位于S-S+的另一条垂线上（在S-S+中垂线右上方），A，B 位于S-S+中垂线上。对MNPQ 这四个出租房源点，按照3.1 中介绍的步骤进行排序有如下的结果：M 优于N，P 优于Q，这样的结果显然是不合理的。因为在M、N 和P、Q 这两对房源点中，N 和P 具有同样的位置，而M 和Q 具有相同的位置，因此对这两组房源点的排序理应为N 优于M，P 优于Q 或者N 差于M，P 差于Q。另外，对于像点A 和点B 这样在S-S+的中垂线上的点所对应的房源的相对贴近度都为0.5，这些房源之间也无法比较优劣性。这也就是所谓的特殊位置的房源无法进行排序的问题。

上述问题，本文做如下改进：

（1）取S+S-延长线上一点G，使得|S+S-|=|GS-|（|•|代表欧氏距离），记点G 所对应的向量为其中我们可以称它为虚拟负理想解。

（2）分别计算第i 个方案到正理想解S+的距离以及到虚拟负理想解S*的距离即

（3）计算各评价对象的相对贴近度并进行排序

3 租房决策支持系统设计

本系统使用Django 搭建，采用B/S 架构进行开发，核心功能模块是离线数据预处理模块和在线决策结果计算模块。

3.1 离线数据预处理模块

数据预处理主要指的是房源数据以及商家数据的处理，这一部分的数据处理需要调用大量的计算资源，并且这些数据也并非实时数据，如将其放入到网站上进行运算，既没有必要还会导致页面卡顿，影响用户的使用体验。本文所采用的租房房源数据来自于链家网上的真实租房数据。来源于真实生活的数据往往因为各种原因导致数据的格式极为复杂多样，比如数据有很多缺失值，包含很多的文本数据没有数字化等等，因此，这些租房房源数据不能直接拿来使用，需要进行数据处理。图3 展示了一部分原始房源数据。

本文采用Pandas 库对租房数据进行相应的处理。首先，除掉包含空值的数据，空数据大多来自于预测价格这一字段，由于有些房源信息不足，系统无法对价格进行预测故其预测价格为空。然后，需要将经度纬度转换为火星坐标并将其拼接在一起，并根据经纬度删除掉重复的房源。最后将文本信息数字化，“1 室1 厅1 卫”这样的字符串拆开，将客厅卧室数分别储存在两个字段中、用房源的预测价格减去标价之后取绝对值也储存到新的字段中；对于商家信息的处理也是类似的，首先取出去除空值，然后去掉重复值。

将房源数据以及商家数据清洗完成后，需要计算每个房源周围1km 范围内各商家的个数，然后将结果与房源数据拼接。具体的步骤是：对于house_df 数据集中某一个房源，根据该房源的经纬度信息循环遍历poi_df 数据集，判断POI 类型、查找符合距离要求的POI 并按照POI 类型进行归类计算，超市便利店个数保存在变量L中，大中小学幼儿园个数保存在变量E 中、公园绿地数保存在变量G 中、医院个数保存在变量H 中、距离最近的地铁站距离保存在变量T2 中。之后再计算房源预测结果与房源标价差值的绝对值，结果保存在变量delta_price 中。该算法的流程图如图4。

数据处理完成后，将数据也存储在数据库中，方便其他模块的使用，图5 展示了部分处理后的房源数据。

3.2 在线决策模型计算模块

在线决策模型计算模块实现了第三章所提出的决策模型，是本系统较为重要的模块，它主要负责三部分的工作：第一部分，将用户输入的内容以及满足要求的房源信息进行处理；第二部分，使用第三章所提出的决策模型进行决策，得到初步的决策结果；第三部分，将决策结果进行加工，使用户更加容易理解。在线决策页面如图6。

在决策结果页面，左上方是一个搜索框，用户可以输入自己对房源的基本要求，右侧是地图的交互区域，左下方是结果列表。我们根据用户在搜索框中输入的条件，为用户提供了前十个合适的房源展示在左侧列表以及右侧的地图中，用户点击列表中的房源标题或者地图中的查看房源详情来进入房源详情页，查看该房源的具体情况。在线决策计算模块的流程图如图7。

租房者在进入租房决策页面后系统会自动判断用户是否登录，如果用户未登录，则弹出登陆注册表单。用户可在租房决策页面输入工作地点、卧室数、客厅数、上班距离、预期价格等租房条件，之后点击搜索按钮。浏览器会判断用户是否登录，如未登录，则弹出登录注册表单让用户完成登录，之后，再次判断用户输入的信息是否有误，如有误则提示用户重新输入，验证通过后，使用Ajax将用户输入的数据传递给Views 中的处理rent_decision_handle 函数中。使用Ajax 的目的是实现不刷新页面也能获取数据的效果。

后台获取到用户输入信息后对数据进行处理，然后查找符合厅室、价格要求的房源，并计算这些房源距离用户工作地点的距离，然后根据用户选择的上班距离，再次进行筛选得到最终的决策矩阵。得到决策矩阵后，调用计算熵权法的函数Cal_Eweight 根据决策矩阵计算指标的熵权值W2，查询数据库找到当前用户的主观权重W1，然后按照公式5 计算出组合权重W。最后，调用编写的TOPSIS 法函数topsis，得到初始的决策结果。将初始决策结果按照相对贴近度从大到小进行排序，取最合适的前十个房源，添加上小区信息、房源图片、房源标题等信息打包为Json 格式数据传递给前端模板，最后使用Javascript 对结果进行展示。

4 总结

本文针对帮助租房者决策挑选合适房源这一现实问题为出发点，提出了改进后的TOPSIS 决策模型，并将该模型应用于实际，设计完成了租房多属性决策支持系统，并开发了一些如登录注册、收藏等辅助功能。租房者可通过该系统顺利的找到自己满意的房源，解决由信息爆炸所带来的找房难的问题。未来，可以对界面美观程度、系统响应速度、人性化程度等方面对系统进行完善，进一步优化用户体验。