基于响应面法的表冷器-风机集放热系统参数优化

何雪颖 王平智,2 李 明,2 宋卫堂,2

(1.中国农业大学水利与土木工程学院， 北京 100083； 2.农业农村部设施农业工程重点实验室， 北京 100083)

0 引言

中国设施园艺发展迅速，是世界上设施园艺面积最大的国家，其产值比露地生产高3～5倍，设施园艺产业为农业和农村经济发展、乡村振兴和农民生活水平的改善作出了巨大贡献[1]。伴随着园艺设施冬季加温需求的日益增长[2-3]，为了减少化石能源消耗，研究者开发了各种清洁能源加温系统[4]。根据园艺设施的光热特性，以太阳能和空气能为热源的集放热系统受到广泛重视，如主动蓄放热系统[5-7]、太阳能水循环集热装置[8]、中空板水循环集放热系统[9]、地中热交换系统[10]、岩床蓄热系统[11]、空气余热热泵系统[12-13]等。寻求低碳、高效、节能的加温技术对于设施园艺的健康可持续发展具有重要意义。

集放热系统高效、节能运行的关键不仅在于系统本身，还在于调控参数的选择[14]。曹晏飞等[15]通过单因素试验测试了风速、空气-土壤温度差对热交换系统热流量的影响，提出优化调控参数。佟雪姣等[16]以集热量为评价指标，通过单因素试验，确定系统设计参数。虽然单因素试验可以反映某单一因素对集放热性能的影响，但在各主要影响因素间存在交互作用时，单因素试验结果不准确，甚至存在极大差异。响应面法常用于模型研究领域中，该方法结合因素筛选、重要因素确定、建模和优化设计，对有代表性的因素水平组合进行试验，用回归方法模拟试验范围内各因素与结果之间的函数关系，从而得到各因素的最优水平[17]。

表冷器-风机集放热系统具有体积小、换热性能好、成本低等优势，可以较好实现对温室温度的控制[18]。但关键因素对系统集放热性能的影响规律尚不清楚，系统的最佳调控参数也尚未确定。本研究以增大系统热流量、提高系统性能系数为优化目标，采用单因素试验探究关键因素对系统集放热性能的影响规律，再通过响应面法得到最优的调控参数组合，以期为集放热系统的参数优化提供可借鉴的方法，为表冷器-风机集放热系统高效、节能的运行提供理论依据和数据支撑。

1 材料与方法

1.1 试验温室和表冷器-风机集放热系统

供试日光温室位于北京通州区中农富通科技园(39.8°N，116.7°E)内，温室东西长50 m，南北跨度8 m，后墙高2.6 m，脊高3.8 m。后墙及两侧山墙均为厚15 cm仅有保温功能的聚苯乙烯发泡板，内表面涂抹抗裂砂浆。在温室长度方向的中间位置，用中空PC板将温室分隔成完全相同的东、西两部分，其中西侧安装表冷器-风机集放热系统作为试验区，东侧作为对照区。

表冷器-风机集放热系统主要由表冷器-风机、供回水管路、潜水泵、蓄热水池、控制系统等组成(图1)。其中，表冷器-风机型号为FNH 9.7/33(浙江瑞雪制冷设备科技有限公司)；潜水泵额定流量5 m3/h，扬程60 m，功率2.2 kW。表冷器-风机安装于温室屋脊下方，分别与供水和回水管路相连接，使水媒在表冷器-风机和蓄热水池之间循环。白天集热时，系统将温室内空气中的余热通过表冷器-风机转移到水中并存储于蓄热水池；夜间放热时，系统再将储存的热能通过表冷器-风机从水中转移到空气中，以提升温室气温。

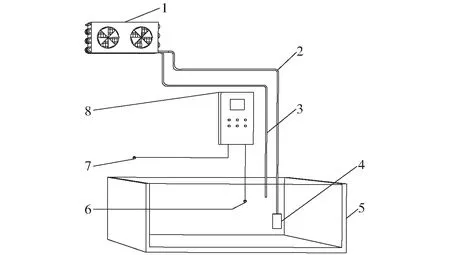
图1 表冷器-风机集放热系统示意图Fig.1 Schematic of air-cooled condenser heat collection and release system1.表冷器-风机 2.供水管路 3.回水管路 4.潜水泵 5.保温蓄热水池 6.控制系统水温测点 7.控制系统气温测点 8.控制系统

1.2 试验方法

系统集热和放热均通过表冷器-风机对流换热实现，传热方式不变。由表冷器-风机风侧、水侧、盘管传热能量平衡可得[19]

(1)

式中φ——热流量，W

vy——风速，m/s

Ta——空气温度，℃

Tw——水温，℃ω——水流速，m/s

ξ——析湿系数，干工况下ξ=1

A、B、m、n、p——对流传热系数的系数和指数

S、Sv、Sw——表冷器-风机的换热面积、迎风面积和水管截面积，m2

ρa、ρw——空气密度和水密度

cp、cw——空气定压比热容和水比热容，水的比热容取4.2×103J/(kg·K)

在系统运行过程中，以水为蓄热媒介，运行条件为干工况，且表冷器-风机型号、进回水管路确定，由式(1)可以看出，水气温差|Ta-Tw|、风速vy、水流速ω是影响系统传热的主要因素。放热和集热是能量传递的互逆过程，Ta-Tw在集热阶段为正值，在放热阶段为负值，各个因素对集热性能和放热性能的影响规律相同。因此，影响系统集放热性能的主要因素为水气温差|Ta-Tw|、风速vy、水流速ω。系统的集放热性能采用热流量进行评价：热流量越大，说明单位时间内的换热量越大；系统的节能性采用性能系数进行评价：系统性能系数越高，说明耗能相对较低。因此，选取水气温差、水流速、风速3个因素，先通过单因素试验，计算各试验条件下的热流量和性能系数，初步确定各因素的优选范围；再通过不同因素水平组合的响应面试验，测试各试验条件下的性能系数，通过建立回归模型，分析因素间的交互作用并最终优化调控参数。

1.3 试验设计

测试过程中，手动控制系统启闭，每次仅运行单台表冷器-风机，通过变频器调节表冷器-风机和潜水泵的转速，以改变风速和水流速。

单因素试验：以热流量和性能系数为评价指标，在水气温差0～11.0℃，水流速0.27、0.52、0.77、1.02、1.27、1.52 m/s，风速0.94、1.40、1.64、1.87、2.11、2.34 m/s的范围内[20]，探究关键因素对系统集放热性能的影响规律，并为响应面法优化提供依据。

响应面法：在单因素试验的基础上，采用三因素三水平Box-Behnken设计方法，选取水气温差(X1)、水流速(X2)、风速(X3)3个因素作为自变量，以性能系数为因变量。系统调控参数和编码见表1。

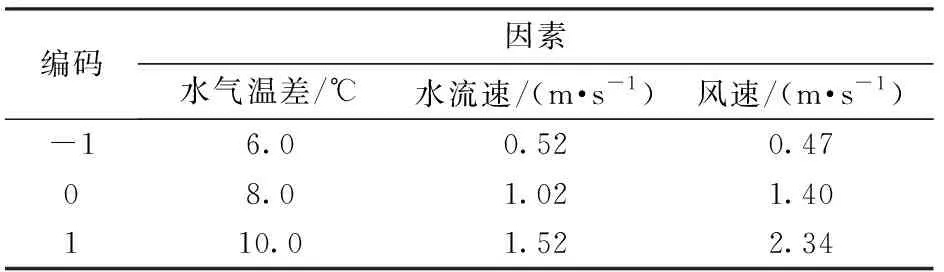
表1 试验因素编码Tab.1 Factors codes of experiment

1.4 测点布置与试验仪器

表冷器-风机的进、回水管路各布置1个水温测点，测点靠近表冷器-风机的进、回水口，试验中水温传感器使用三线制铠装Pt100，精度为±0.2℃。

表冷器-风机进、出风两侧各布置1个气温测点，测点位于距表冷器-风机0.5 m的中心位置，试验中空气温度传感器采用普通三线制Pt100，精度为±0.2℃。

温度数据采集选用无纸记录仪(杭州联测自动化技术有限公司，LR204D型，精度±0.2%)，数据采集间隔为1 min。

风速采用5点测量法，使用手持式热线风速仪(KANOMAX 6036-BC型，精度±0.01 m/s)测量，人工记录。

耗电量和水流量分别使用电能表(上海华立电表厂，精度±1%)、水表(北京京海恒隆科技开发有限公司，精度±2%)测量，人工记录。

1.5 评价指标

表冷器-风机集放热系统单位时间的换热量即为热流量，计算式为

(2)

其中

Q=τcwωρw(Tw1-Tw2)

(3)

式中Q——表冷器-风机换热量，J

τ——运行时长，s

Tw1、Tw2——表冷器-风机的进水、出水温度，℃

性能系数COP计算式为

(4)

式中E——集热阶段或放热阶段耗电量，J

1.6 不确定度分析

不确定度用于表明测量结果的可信赖程度，便于他人评定测量结果的可靠性。不确定度越小，所述结果与被测量的真值越接近，质量越高；不确定度越大，则相反。各测量值相对不确定度计算式为[21]

(5)

(6)

(7)

(8)

(9)

式中UA——A类不确定度

n——测量次数

xi——第i次测量数据

UB——B类不确定度

ΔUins——仪器误差

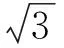
Uc——合成不确定度

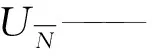
Ur——相对不确定度

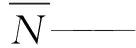
不确定度计算数据及结果如表2所示。

表2 不确定度计算数据及结果(置信度为95%)Tab.2 Uncertainty calculation data and results(95% confidence level)

2 结果与分析

2.1 单因素试验

2.1.1水气温差对热流量和性能系数的影响

图2为在水流速为1.52 m/s、风速为2.34 m/s条件下，热流量和性能系数随水气温差变化的曲线。从图2可以看出，热流量与水气温差呈正比关系，水气温差为0、11.0℃时，热流量实测值分别为0.16、8.14 kW，其拟合方程为φ=0.726|Ta-Tw|，即水气温差每增大1.0℃，热流量可增加0.726 kW。性能系数随着水气温差的增大而线性升高，水气温差为0、11.0℃时，性能系数实测值分别为0.1、6.4，拟合方程为COP=0.548 5|Ta-Tw|-0.049 4，即水气温差大于1.9℃时，性能系数大于1。

图2 不同水气温差下的热流量和性能系数Fig.2 Heat transfer rate and COP under different water and air temperature differences

系统运行时对流传热系数、传热面积为定值，由牛顿冷却原理可知，对数平均温差随水气温差增大而增大，因此热流量呈线性增大。系统运行过程中水气温差的改变是由园艺设施本身的结构特点和天气条件等引起的，但运行能耗没有改变，即式(4)中耗电量E为定值，因此，性能系数与热流量变化规律一致，即随水气温差的增大，性能系数与热流量均呈线性增大。

目前已有的集放热系统中，系统集、放热启动的时间或条件和控制方法等都缺少理论依据。如佟雪姣等[8]将系统运行时间设定为10:00—15:00和00:30—06:30，依据自然时刻启动的方式常凭经验设定，阴天和晴天运行条件有较大差异[23]，不能判断室内热能是否富余。YANG等[12]在温室气温高于26℃和低于18℃时分别进行集热和放热。仅依据室内气温决定系统启动的方式，可能出现系统逆向传热，如满足集热运行条件时水温高于气温处于放热状态，或放热运行阶段处于集热状态。邱仲华等[24]将系统集热启动条件设定为温室气温高于水温。由室内气温和水温共同控制的启动方式，可有效判断室内的热能以及系统运行情况，避免室内富余热能损失以及逆向传热等，如图2所示，水气温差越低，热流量和性能系数越低，可见较小温差不利于系统高效、节能运行。XU等[9]通过监测模拟集热器表面温度和水温，将系统运行条件设定为模拟集热器表面温度与两者温差共同控制，但对实际运行中的设定值并未给出理论解释。表冷器-风机集放热系统主要通过对流实现集热和放热，根据牛顿冷却原理，系统运行时水流速与风速不变，即传热系数与换热面积均不改变，水气温差是影响系统高效换热、节能运行的关键因素，因此以空气温度与循环水温度共同控制，且由图2可知选定合适的水气温差是系统高效、节能运行的基础。

以单台表冷器-风机加热温室面积为120 m2，系统集热时长为4～5 h[18]为例，单个夜晚所需加温热量为60～100 kJ/(m2·K)[25]，将室温提升5℃，所需的集热量为36～60 MJ，则单台表冷器-风机的热流量为2.0～4.2 kW，由图2模拟方程计算可知水气温差为2.8～5.8℃，此时性能系数为1.5～3.1。如番茄生产温室白天最适温度为25～28℃，夜间温度不低于10℃，则系统启动条件可设定为气温高于25℃且高于水温5.8℃时集热，气温低于10℃且低于水温5.8℃时放热。

如图3所示，水气变化曲线为系统实际运行过程中测试所得。08:00揭开保温被后，水气温差迅速增大，甚至高于10℃，持续一段时间后开始下降，随着气温的下降，至16:00左右为0℃。然后，再随着气温的进一步降低而持续降低，直至系统开始放热，水气温差逐渐缩小或达到基本稳定。这是由于水作为比热容较大的蓄热介质，在白天系统集热时水温以较慢速率逐渐升高，空气受太阳辐射影响气温升高或降低迅速；夜间系统放热时将水中热能释放到空气中，水温逐渐降低，气温保持稳定。从图3可以看出，10:30开始集热，此时水气温差为10.8℃，至14:45集热结束时水气温差为-8.6℃；19:55开始放热时水气温差为-6.9℃，至次日08:00水气温差逐渐降低至-4.4℃。可见，在系统集热阶段，水气温差始终高于设定值，温室气温可以作为主要的控制条件，集热流量与集热性能系数均高于预期，水气温差设定在建议的范围内即可；在系统放热阶段，水气温差逐渐缩小直至不满足条件，系统停止运行，水气温差成为放热阶段的主要控制条件，放热流量和放热性能系数与预期一致，因此在建议的范围内，选择较高的水气温差有利于系统高效、节能运行。

2.1.2水流速对热流量和性能系数的影响

图4为在水气温差为8℃、风速为2.34 m/s条件下，热流量和性能系数随水流速变化的情况。相同条件下随着水流速增大，热流量呈上升趋势，但热流量的升高速率随着水流速的增大而减小，水流速为0.27～1.52 m/s时，热流量实测为1.89～5.37 kW，其拟合方程为φ=-1.998ω2+6.209 3ω+0.487 8。性能系数随水流速的增大，先增大后减小。实测数据显示，水流速为0.27～1.02 m/s时，性能系数从2.7增至4.0，水流速为1.02～1.52 m/s时，性能系数从4.0减至3.7。根据拟合方程COP=-1.628ω2+3.685 1ω+1.858 1可知，当水流速为1.13 m/s时性能系数最高。

图4 不同水流速下的热流量和性能系数Fig.4 Influence of different water flow velocities on heat transfer rate and COP

水流速的增大主要影响表冷器-风机的进出水温度，进而使得对流传热系数增大[20]。根据牛顿冷却原理，固定条件下表冷器-风机的进风温度和进水温度不变，随着水流速的增加，表冷器-风机的出口水温逐渐趋近于进口水温，单位时间内换热量增大，则热流量增大。当水流速无限增大时，表冷器-风机进出口的水温差逐渐趋近于零，对流传热系数增大趋近于某一数值，热流量也增加趋近于某一数值。实际上，水流速并非越大越好，增大水流速，管道压力和阻力将会随之增大，需要提升水泵扬程和流量，水泵能耗增长越来越快[26]。由于热流量的增加速率高于系统能耗的增加速率，性能系数呈上升趋势，由于系统能耗的增加速率高于热流量的增加速率，性能系数开始下降。因此，性能系数呈先上升后下降的趋势。

2.1.3风速对热流量和性能系数的影响

风速增大主要影响进出空气温度，进而使得对流传热系数增大。根据牛顿冷却原理，固定条件下表冷器-风机的进风温度和进水温度不变，随着风速的增加，表冷器-风机的出口气温逐渐趋近于进口气温，单位时间内换热量增大，则热流量增大。当风速无限增大时，表冷器-风机的进出气温差逐渐趋近于零，对流传热系数增大趋近于某一数值，热流量也增加趋近于某一数值。而风速也并非越大越好，增大风速，通风阻力会随之增大，风机能耗增长的速度越来越快[27]，因此性能系数呈先上升后下降的趋势。

2.2 系统调控参数的响应面法优化

以水气温差(X1)、水流速(X2)、风速(X3)为响应变量，热流量(Y1)与性能系数(Y2)为响应值建立模型。应用Design-Expert软件对表3中的数据进行多元回归分析，得到热流量与性能系数编码因素模型方程分别为

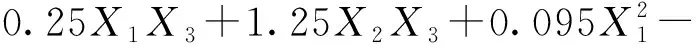
(10)

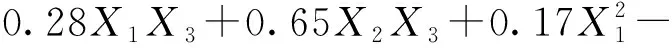
Y2=5.42+1.08X1+1.16X2+1.59X3+0.48X1X2+

(11)

表3 正交试验设计与结果Tab.3 Design and results of response surface analysis

热流量与性能系数实际因素模型方程分别为

Y1=-0.61|Ta-Tw|-2.39ω+4.71vy+
0.70|Ta-Tw|ω+0.14|Ta-Tw|vy+2.20ωvy+

(12)

Y2=-0.70|Ta-Tw|+3.62ω+4.29vy+
0.39|Ta-Tw|ω+0.15|Ta-Tw|vy+1.14ωvy+

(13)

响应面二次模型方差分析结果见表4、5。模型P<0.01，说明模型对热流量及性能系数有显著意义。失拟项P>0.05，意味着由误差引起的失拟不显著；模型决定系数R2为0.963 6和0.915 8，表明响应值的变化有96.36%和91.58%来源于所选变量，预测值和实测值之间的相关性高。由此可见，该模型是有效的，能正确反映Y1、Y2与X1、X2、X3之间的关系，可以用来分析和预测结果。

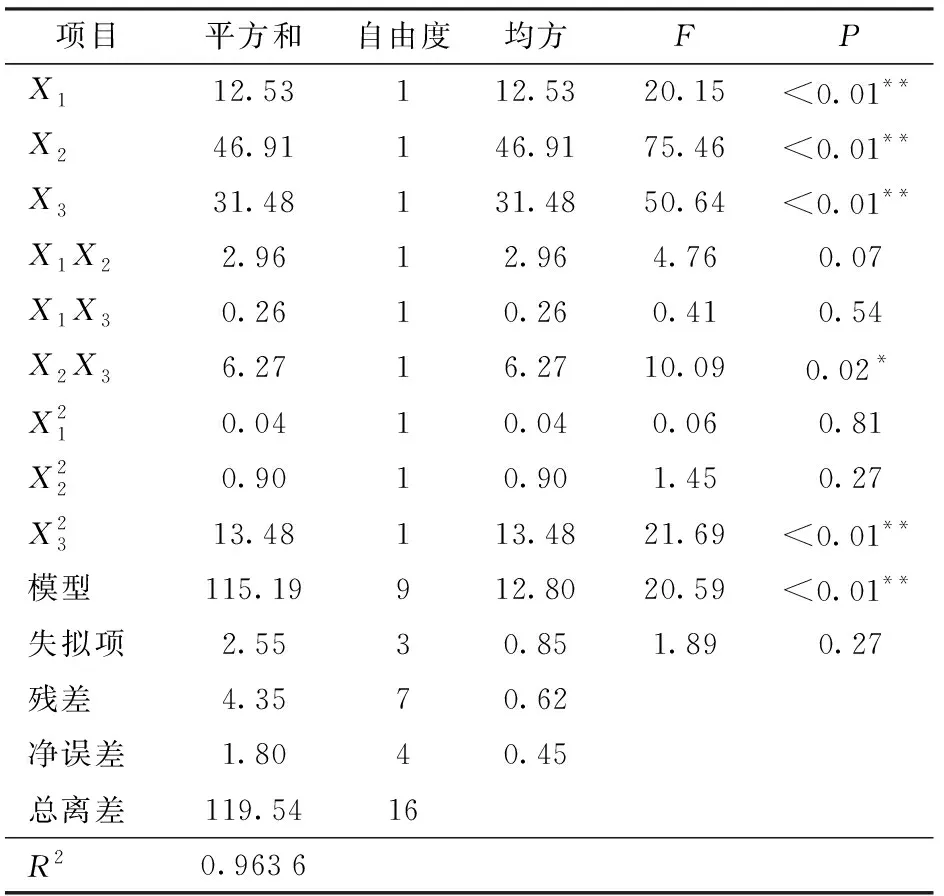
表4 热流量回归模型方差分析Tab.4 Analysis of variance (ANOVA)of heat transfer rate regression model

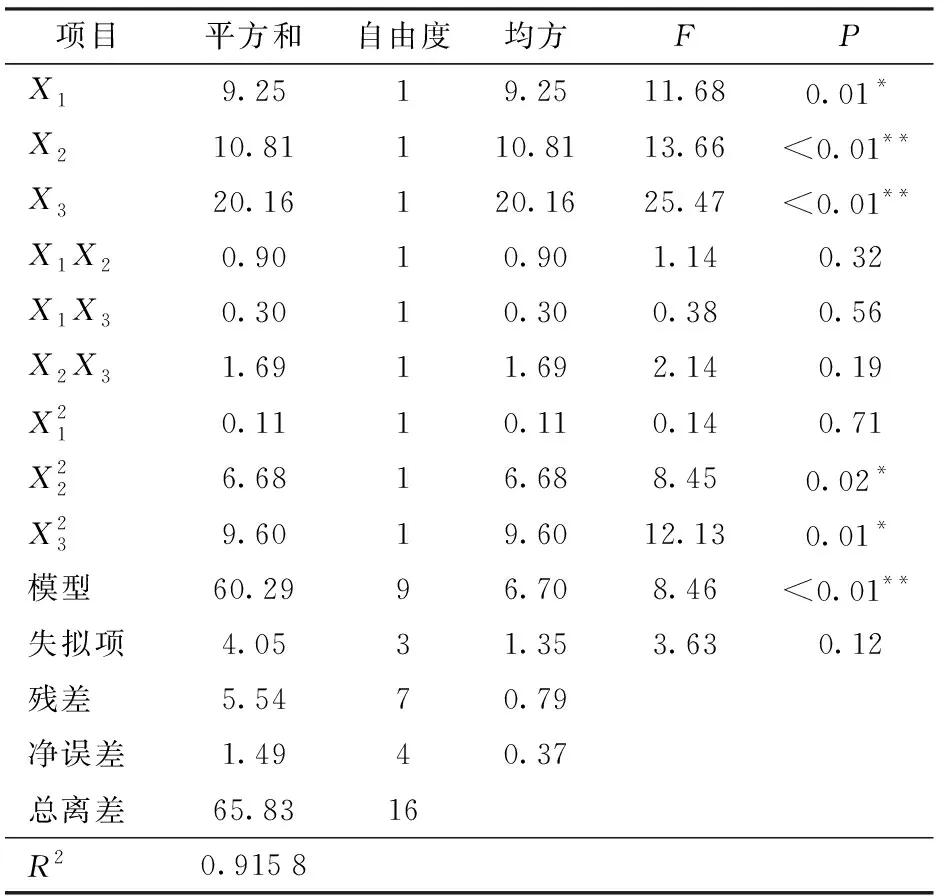
表5 性能系数回归模型方差分析Tab.5 Analysis of variance (ANOVA) of COP regression model

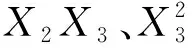
响应曲面坡度越陡说明该因素的影响越显著，在因素发生变化时热流量和性能系数的响应灵敏，如图6所示，与表4、5中交互项P值的分析结果一致。如图6a～6c所示，热流量随水气温差、水流速、风速的增大而增大，仅由热流量不能得到最佳调控参数。如图6d所示，性能系数随水气温差的升高而增大，水气温差低于8.5℃时，无论水流速如何变化，性能系数不高于6。如图6e所示，当水气温差高于8.3℃时，对性能系数的影响显著。由图6f可以看出，性能系数随水流速和风速的增大先增大后减小，响应面图的最大点位于试验区内部，表明通过响应面试验可以获得最佳调控参数，使性能系数最大化。

图6 因素间交互作用对热流量和性能系数影响的响应曲面Fig.6 Response surface diagrams of interaction influence between factors

优化分析可得，当水气温差设为5.8℃时，水流速1.23 m/s、风速1.91 m/s为表冷器-风机集放热系统最佳调控参数，此时预测热流量为5.88 kW，性能系数为4.9。

3 讨论

应用响应面法优化集放热系统参数来提升系统性能是可行的。由前期研究可知[18]，表冷器-风机集放热系统应用于轻质墙体日光温室时，其控制策略为气温高于22℃且高于水温5℃开始集热，气温低于13℃且低于水温2℃开始放热，系统运行的集热性能系数为3.4～4.9，放热性能系数为0.9～3.2；应用于柔性保温后墙日光温室的控制策略为气温高于23℃且高于水温3℃开始集热，气温低于10℃且低于水温3℃放热，则系统集热性能系数为5.7，放热性能系数为1.3～1.8。可见，调控参数对放热阶段的节能性影响较大，优化后系统的放热性能系数不低于4.9，提升35%～82%，显著提升了系统的节能性。

优化调控参数有利于降低系统成本。优化后表冷器-风机集放热系统的集热性能系数和放热性能系数均为4.9。孙维拓等[13]研发的日光温室空气余热热泵加温系统，其集热性能系数为3.3～4.2，放热性能系数为3.8～4.1；YANG等[12]研究的温室空气余热热泵系统，其性能系数为2.32～3.55。与上述其他空气热源加温系统相比，表冷器-风机集放热系统减少了热泵、水泵的投入成本，运行成本也相对较低。

采用响应面法优化此类集放热系统的调控参数，能够提升系统集放热性能；同时，该研究也为表冷器-风机集放热系统的配置、控制策略提供了数据参考，对表冷器-风机集放热系统的发展具有积极意义。但表冷器-风机集放热系统仍处于研发和推广的初级阶段，为便于测试表冷器-风机的集放热性能变化规律，试验中仅测试一种结构的表冷器-风机。表冷器-风机结构对传热性能有影响[28]，在后续的试验中可以进一步研究其他表冷器-风机结构的调控参数模型。

4 结论

(1)仅单因素变化时，在测试范围内表冷器-风机集放热系统的热流量随着水气温差的增大呈线性增大；随着水流速或风速的增大，热流量一直增大，但增加趋势逐渐变缓。性能系数随水气温差的增大呈线性增大；随着水流速或风速的增大，性能系数呈先增大、后减小的趋势。

(2)采用响应面法建立了水气温差、水流速、风速与热流量和性能系数的二次多项式回归模型，模型决定系数R2分别为0.963 6和0.915 8，表明预测值和实测值之间的相关性较高。说明响应面法应用于温室集放热系统的参数优化是可行的，本文为此类集放热系统高效、节能运行提供了一种参数调控优化方法。

(3)3个影响因素对热流量的影响从大到小依次为水流速、风速、水气温差，对性能系数的影响从大到小依次为风速、水流速、水气温差。系统的最佳调控参数：风速为1.91 m/s，水流速为1.23 m/s，水气温差5.8℃，此时热流量为5.88 kW，性能系数为4.9。