基于类属特征和依赖标记的多标记分类算法

秦梦莹，秦锋

（安徽工业大学计算机科学与技术学院，马鞍山243000）

0 引言

随着信息技术的迅速发展，互联网中存在着大量的多标记数据，如何高效地处理这些多标记数据是当前研究的热点问题。传统的单标记监督学习框架在处理这些多标记数据时难以取得很好的效果，基于此多标记学习框架应运而生。现如今多标记分类问题作为多标记学习研究的主要问题被广泛运用于各个领域，如信息检索、文本分类、图像识别、生物信息学、音乐情感分类等。

在多标记分类问题中，数据的特征维度通常会影响到算法的最终分类性能，冗余和不相关的特征不仅会降低分类器的精度，而且会导致算法运行的速度变慢。多标记特征选择技术是解决数据特征维度过高的一种有效方法，特征选择是指从原始特征空间选择出最小的特征子集并且不改变原始特征空间信息，当前一些多标记特征选择方法通常使用标记与特征之间的互信息[1-5]作为评判相关特征的标准，根据阈值设定以删除不相关的特征。但上述多标记特征选择方法并没有利用类属特征[6]的概念以进行特征选择，类属特征是指与每个标记最相关、对该标记最具有判别能力的特征，例如可以认为特征“气温”、“海拔”是类别标记“高原”的类属特征，特征“音色”、“频率”可作为类别标记“鸟声”的类属特征，构造类属特征以进行特征选择可以有效缓解决数据特征维度过高的问题，与传统多标记特征选择方法相比基于类属特征的多标记学习方法则更充分考虑了标记与特征之间的联系。

类别标记之间往往不是相互独立的，而是存在一种相互依赖的关系，依赖关系反映了标记之间的相关性，如在图像标注中，标记“大海”和“沙滩”则可称之为依赖标记，一篇体育类文档，标记“运动员”、“比赛”和“排名”也可构成依赖标记。现有多标记分类学习算法根据标记相关性程度可以被分为三大类[7]：“一阶”策略，“二阶”策略，“高阶”策略。“一阶”策略是指将多标记分类问题分解为与类别标记个数相同的多个二元分类问题，对每一个类别标记都训练各自的分类器，典型的“一阶”策略算法如二元关联算法（Binary Relevance，BR）[8]，基于K近邻的多标记算法[9]，“一阶”策略算法的时间复杂度与数据集的标记数量呈正比，“一阶”策略虽然概念简单但忽视了标记之间的相关性。“二阶”策略考虑了标记之间的成对关联性，典型的“二阶”策略算法如校准标记排序算法（Calibrated Label Ranking，CLR）[10]利用每个示例的相关标记与无关标记的排序关系求解多标记分类问题，但在实际应用中，标记相关性往往超出了二阶假设。“高阶”策略则充分考虑了所有类别标记之间的全局相关性来解决多标记学习任务，如文献[11]提出了集成链式分类器方法通过构造多条链式分类器以考虑标记全局相关性，但高阶模型通常复杂度较高且存在误差传播问题。

针对上述问题，本文提出了一种基于类属特征和依赖标记的多标记分类算法（Multi-label Classification Algorithm Based on Class-specific Features and Depen⁃dent Labels，CFDL），CFDL算法的主要贡献如下：

（1）通过构造标记的类属特征集以去取冗余或不相关的特征。

（2）根据依赖标记之间的相关性，构造基于标记高阶相关性的分类模型。

（3）在测试阶段通过类属特征与依赖标记之间的联系以生成预测标记，从而无需借助外部分类器进行分类预测。

（4）对比实验结果表明CFDL算法在处理多标记分类问题的优越性。

1 相关工作

类属特征反映的是每个标记最相关最具判别性的特征，因此构造类属特征有助于确定每个示例的相关标记集合。文献[12]通过聚类集成技术考虑标记关联性以生成类属特征，文献[13]使用线性回归模型从非稀疏场景中提取数值型标记的类属特征以构建更具竞争性的多标记分类器，文献[14]则提出将l1范数与l2,1范数结合同时对特征空间到标记空间的投影矩阵作正则约束，用以提取共享特征和类属特征，文献[15-16]则结合类属特征和局部标记相关性用于处理类不平衡问题。在构建类属特征的过程中可能会致使特征空间产生冗余信息，文献[17]提出利用模糊粗糙集对类属特征约简以降低类属特征的维数，文献[18]通过综合利用随机子空间模型及成对约束降维思想提取更有效的特征信息。

链式分类器（Classifier Chain，CC）[11]是一种常见的链式多标记分类方法，与BR方法不同的是链式分类器考虑了标记之间的相关性，CC方法将多标记分类问题被转化为多个二元分类器链，且前一个分类器的标记输出结果将作为后一个分类器的附加输入信息，因此链式分类器也常被用于构建标记高阶相关性模型。如文献[19]提出构造多条环形分类器链用于解决CC方法中标记顺序影响分类性能的问题。文献[20]提出构造树形结构的分类器链用于搜索标记的相关特征子集。文献[21]则将链式分类模型用于处理元标记（meta-la⁃bel）的分类预测。链式方法通常只捕获标记之间的部分依赖关系，堆叠方法（stacking）则可以在将冗余度引入特征空间的同时，捕获标记的完全依赖性。如文献[22]提出的修剪可信堆叠方法可以使多个分类器链在测试阶段并行运行，同时通过计算所有所有成对标记的信息增益值来删除低于给定阈值的不必要标记依赖关系。文献[23]提出的基于帕累托最优（Pareto Opti⁃mum）的堆叠模型选择出最相关的标记子集再进行标记预测，最终在测试阶段使用选定的标记子集和扩展特征得到预测结果。文献[24]提出以堆叠稀疏方式学习类属特征和依赖标记学习了依赖标记之间的高阶相关性。链式方法和堆叠方法虽然能有效反映类别标记的全局相关性，但由于结构的特殊性也会导致误差传播问题，例如前一个分类器的预测错误将会沿链传播到下一个分类器或者上一层的分类预测错误会影响到下一层的分类预测。

本文提出的CFDL算法将通过l1范数正则约束构造稀疏的类属特征集，同时为避免高阶多标记分类算法因使用外部分类器而导致误差传播问题，CFDL算法将根据类属特征和依赖标记之间的联系以生成预测标记。

2 CFDL算法

2.1 多标记分类问题的相关定义

令X=Rd表示d维特征空间，表示q维标记空间，给定一个包含n个样本的多标记数据集，其中表示特征向量，表示标记向量，如果第i个示 例xi含有 标记yj，则yij=1，否则yij=0，令X=[x1,x2,…,xn]T∈Rn×d表示输入数据，Y=[y1,y2,…,yn]T∈Rn×q表示真实标记集合。

2.2 类属特征和依赖标记

类属特征应当是每个标记最相关、最具判别性的特征，因此标记的类属特征集中所包含的特征个数应远小于原始特征空间的特征数目，使用表示特征空间到标记空间对应的类属特征矩阵为第j个标记所含有的类属特征中的非零元素则说明该特征可作为标记j的类属特征，否则不是标记j的类属特征，通过构造类属特征集可以有效解决数据特征维度过高的问题。

通常认为关联性很强的标记之间比关联性较弱的标记之间存在更多相同的类属特征，因此挖掘标记之间的关联性将会有助于类属特征的提取，把关联性很强的标记称之为依赖标记，令表示依赖标记矩阵，表示与第j个标记相关的所有依赖标记中的非零元素表示两个标记之间构成依赖标记中的零元素则说明两个标记之间关联性较弱或者不相关，Wy的提出可以反映标记集中所有标记之间的相互依赖关系。

采用最小二乘作为损失函数用来判断预测值与真实标记之间的误差，得到的优化问题如下：

在测试阶段输出标记Y需使用现有的分类器得出，如果使用额外的分类器进行标记预测可能会出现误差传播的问题，从而降低算法的分类性能，为避免上述问题，可将目标函数中的输出标记矩阵Y视为一个变量并改写为其他形式，令l表示式（1）所示的损失函数，由，可得，其中I∈Rq×q为对角线元素全为1的单位矩阵,使得测试阶段的输出标记可由类属特征矩阵和依赖标记矩阵确定，由此得到的优化问题如下：

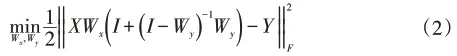
考虑到并不是所有类属特征和标记依赖关系都有助于提升算法性能，因此需要对类属特征矩阵和依赖标记矩阵使用l1范数正则化以去除冗余的类属特征和依赖标记，最终获得较为稀疏的类属特征矩阵Wx和依赖标记矩阵Wy，即让Wx和Wy获得尽可能多的零元素，得到的基于标记高阶相关性的线性分类模型如下：

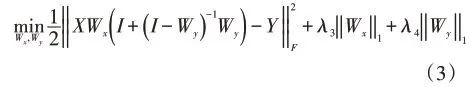
其中λ3、λ4为非负权衡参数。

令C∈Rq×q表示标记相似度矩阵，标记之间的相关性程度可由余弦相似度计算（cosine similarity），余弦值越大，说明两个标记越相似，即标记的关联性越强，使用ci,j表示矩阵C中任意两个标记yi和yj之间的余弦相似度则标记空间中任意两个标记之间的相关性可通过获得，任意两个标记之间的类属特征共享性可通过获得，由此得到的优化问题如下：

其中λ1，λ2为非负权衡参数，令:

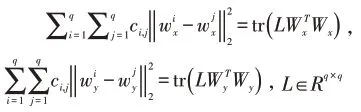
因此可将（4）式写为如下优化问题：

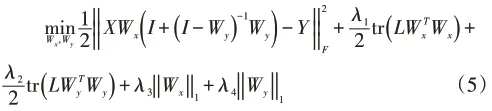
由此可得CFDL算法的优化问题如（5）式所示，其中λ1≥0，λ2≥0，λ3≥0，λ4≥0为权衡参数，λ1控制标记与特征之间的关联性，λ2控制标记之间的关联性，λ3控制类属特征的稀疏性，λ4控制依赖标记的稀疏性，待求解的Wx∈Rd×q为类属特征矩阵，Wy∈Rq×q为依赖标记矩阵。

3 优化求解

（5）式中由于l1范数正则项的引入，导致目标函数的非平滑性，提出了算法1采用加速近端梯度方法（Accelerated Proximal Gradient）求解该非平滑凸优化问题，令F(·,·)表示（6）式如下所示：

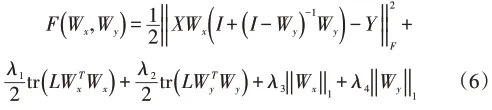
代替直接最小化F(·,·)，可将F(·,·)分成两部分f(·,·)和g(·,·)求解：

H为希尔伯特空间（Hilbert space），其中f(·,·)和g(·,·)分别表示如下：

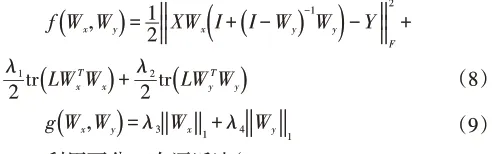
利用可分二次逼近法（Separable Quadratic Approxi⁃mations）求解（10）式可得到（6）式的解：

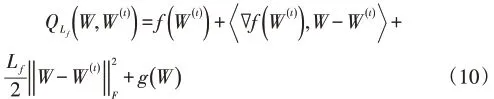
其中Lf为利普希茨常数（Lipschitz constant），根据文献[25]Lf可由线性搜索策略获得。和分别为Wx和Wy的第t次迭代。

3.1 更新Wx

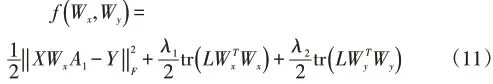
由（11）式对Wx求梯度可得：

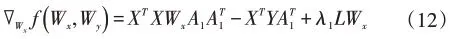
根据文献[25]中加速近端梯度的求解方法，以如下形式更新表示Wx的第t次迭代，其中αt满足由线性搜索策略获得。

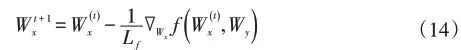
Wx以如下方式优化：

考虑到（15）式中l1范数正则项的存在，可对Wx中的每一个元素分别执行软阈值函数作进一步处理，令proxε()∙表 示 软 阈 值 函 数，wij∈R，且ε>0，()∙+=max(∙,0)，则proxε()∙定义如下：

3.2 更新Wy

令A2=XWx，则（8）式可写为：

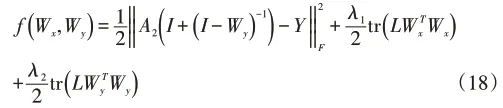
由（18）式对Wy求梯度可得：

根据文献[25]中加速近端梯度的求解方法，以如下形式更新表示Wy的第t次迭代。

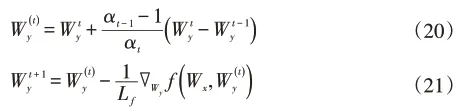
其中αt满足由线性搜索策略获得。

Wy以如下方式优化：

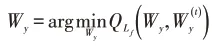
算法1 CFDL算法优化求解

4 实验分析

4.1 数据集与对比算法

为验证CFDL算法分类预测的有效性，本文将在六个不同规模的多标记数据集（http://mulan.sourceforge.net/datasets.html）上与ML-KNN、MLSF、LIFT、LLSF-DL四种多标记分类算法进行对比实验，数据集的具体信息如表1。

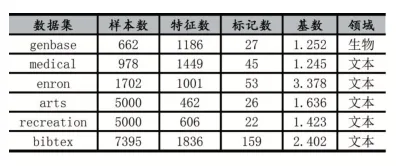
表1 多标记数据集

对比算法的具体实验信息如下：

（1）ML-KNN[9]：ML-KNN算法将传统的K近邻算法引入多标记学习，根据未知示例的相邻示例标记集来获得该示例可能的所属类别信息，最后利用最大后验概率确定未知示例的标记集。近邻个数k∈{8,9,10,11,12}，平滑参数s=1。

（2）LIFT[6]：LIFT算法首先对每个标记的正类样本和负类样本分别进行聚类分析，由此来构造每个标记的类属特征，然后为每个标记来训练二元分类模型。比率参数r∈{0.1,0.2,0.3,0.4,0.5}。

（3）MLSF[21]：MLSF算法首先通过标记间的依赖关系构造元标记（meta-label），其次为每个元标记选择所属的类属特征，最后构造链式结构的分类器以进行标记预测。参数设置K∈{2,4,6,8,10,12,14,16}，γ∈{0.001,0.01,0.1,1}。

（4）LLSF-DL[24]：LLSF-DL算法以堆叠稀疏的方式学习依赖标记的高阶相关性用于处理多标记分类问题。权衡参数α,β,γ∈{4-5,4-4,…,45}，ρ∈{0.1,1,10}。

（5）CFDL：本文提出的基于类属特征和依赖标记的多标记分类算法，利用类属特征和依赖标记之间的联 系 以 获 得 预 测 标 记。权 衡 参 数λ1,λ2∈{100,101,…,105}，λ3,λ4∈{10-1,100,…,104}。

4.2 评估指标

（1）Subset Accuracy：考察标记子集的准确率，对于给定的多标记样本如果预测标记集与真实标记集相同返回1，否则返回0，该评估指标的值越大表示系统性能越优。

（2）F1 measure：F1评估指标考察的是每个样本精确率和召回率的加权平均，该评估指标的值越大表示系统性能越优。

其中pi和ri分别表示第i个样本的精确率和召回率。

（3）Micro F1：F1微平均考察的是总体样本的F1分数，该评估指标的值越大表示系统性能越优。

（4）Macro F1：F1宏平均考察的是每个标记精确率和召回率的加权平均，该评估指标的值越大表示系统性能越优。

其中pi和ri分别表示第i个样本的精确率和召回率。

4.3 实验结果分析

对于每个数据集，每次实验随机抽取80%的样本作为训练集，剩余的20%作为测试集，观察每种多标记算法在不同数据集上的性能表现，重复实验10次取平均值作为实验结果，最终的实验结果如表2-表5所示，粗体表示最优的算法结果，↑表示该评价指标的值越大算法性能越优。

本文通过Nemenyi检验对比各算法在不同评价指标上的相对性能排名，结果如图1所示。Nemenyi检验反映的是不同算法之间的性能差异大小，如果任意两个算法的在评估指标上平均排名大于临界差异值（Critical Difference，CD），则认为两个算法之间的性能差异较明显，k为算法个数，N为数据集个数，在显著水平α=0.05的情况下查表得qα=2.728，由此计算出CD值为2.4903（k=5,N=6），图1中红线连接的算法表示在该评价指标下性能差异不明显，未连接红线表示算法性能差异明显。观察表2-表5及图1可以看出，CFDL算法在六种不同数据集上都取得了不错的分类效果，其中在Subset Accuracy评估指标上CFDL算法与LLSF-DL算法、MLSF算法性能差异并不明显，但优于ML-KNN算法，在F1 measure、Micro F1和Macro F1评估指标上CFDL算法均处于性能平均排名第一位。与一阶算法ML-KNN、LIFT相比CFDL算法充分考虑了标记之间的关联性，与高阶算法MLSF和LLSF-DL相比CFDL算法在测试阶段可以通过类属特征矩阵和依赖标记矩阵直接获得输出标记，避免了高阶算法在使用外部分类器导致的误差传播问题，这也在一定程度上提升了CFDL算法的分类性能。

表2 对比算法在Subset Accuracy上的实验结果

表3 对比算法在F1 measure上的实验结果

表4 对比算法在Micro F1上的实验结果

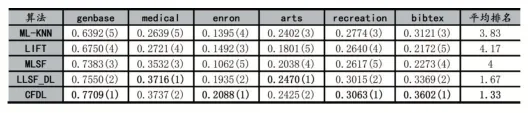
表5 对比算法在Macro F1上的实验结果

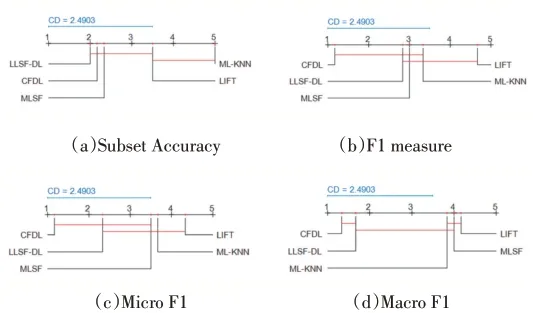
图1 使用Nemenyi检验分析（α=0.05）CFDL算法与其他算法的性能差异

4.4 参数分析

由目标函数（5）式可知，权衡参数λ1控制标记与特征之间的关联性，λ2控制标记之间的关联性，λ3控制类属特征的稀疏性，λ4控制依赖标记的稀疏性。以数据集enron为例，参数设置的最优值为λ1=103，λ2=103，λ3=102，λ4=103，在参数敏感性实验中每次实验只变化其中一个参数，以最优值固定另外三个参数，观察CFDL算法在不同评价指标上的分类性能随参数变化情况，其中λ1和λ2的搜索范围为{100,101,…,105}，λ3和λ4的 搜 索 范 围 为{10-1,100,…,104}。由图2（a）可知，当λ1过小时，四种评价指标的值会减小为0，由图2（b）和图2（d）可知，变化λ2和变化λ4对分类性能影响不大，由图2（c）可知，当λ3过大时，四种评价指标的值会迅速减小为0。

5 结语

CFDL算法通过构造类属特征集和依赖标记集以进行多标记分类任务，同时针对“高阶”策略可能存在的误差传播问题，CFDL算法在测试阶段无需借助外部分类器即可生成预测标记，多个数据集上的实验结果也反映了CFDL算法分类的准确性与有效性。今后将对类属特征集与依赖标记集的构造作进一步研究。

图2 参数敏感性分析