传承文化与智慧，让数学更有味

陈怀兵

[摘  要] 勾股定理在初中数学的教学过程中起着非常重要的作用. 从知识与技能角度来看，它是解决很多数学问题的工具、定理，是关键，是核心;从文化传承角度来看，它是古今中外数学研究者的智慧结晶. 因此，在教学过程中，我们要充分挖掘这种价值与内涵，让文化与智慧传承，让数学有味.

[关键词] 勾股定理;传承;数学;智慧

在“勾股定理”（第2课时）的教学过程中，我们要进一步加深学生对勾股定理的理解，并引领学生站在多个维度、视角去分析、验证勾股定理，感悟知识与技能的融通性、连贯性，并在体验中进一步建构对勾股定理的认识深度和广度，促进学生基本数学素养的进阶提升.

■ 温故知新，素养递进

在前面一节课的学习过程中，我们已经引导学生采用逆向思维的方法来证明勾股定理的存在. 在这个过程中，我们可以采用问题链的方式来启发学生对所学内容进行思考，并在问题中注重方法与策略的渗透，以此提升学生的学习能力和思维能力.

问题1：昨天我们是采用什么方法来验证勾股定理的？

问题2：你能举一个例子吗？

问题3：若一个三角形的三边长分别为a，b，c，且满足a2+b2=c2，则这个三角形是直角三角形吗？

问题4：你能再举一些例子吗？

在整个温故的过程中，我们让学生思维再现，兴趣倍增. 学生在温固的过程中，先经历特殊数据的列举，再到一般特征的提炼. 这一思维过程，也是我们揭秘发展规律的关键策略. 到此，学生已经从方法与技能层面掌握了前一节课的学习，也对勾股定理有了一个初步的认知，为此，我们需要进一步激发学生的思维，拓展学生的视野，于是教师继续追问学生.

问题5：在漫长的岁月里，古代的数学研究者是怎么发现勾股定理的？你听说过吗？

这样的问题起到了承上启下的作用. 对孩子而言，是兴趣的激发，思维的再引领，并暗示学生，在验证勾股定理的过程中，除了用上面的逆向思维方法以外，还有其他方法.

■ 多样体验，别样收获

为了进一步挖掘证明勾股定理的方法，并让学生深刻感受古代数学家的智慧与精神，我们可以采用以下几个环节来还原学生的实践体验过程，让学生领略不一样的收获，体会不一样的数学味.

1. 展示“青朱出入图”

教师给学生展示如图1的“青朱出入图”，并提问学生：你们知道我国古代数学家刘徽是怎样通过以形助数的方法来证明勾股定理的吗？《九章算术》中留下了一段文字，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不动也，合成弦方之幂. 开方除之，即弦也”，后人根据这段文字补了一张图，如图1. 这一介绍让学生对刘徽的证明方法兴趣倍增，也让他们开始思考怎样才能经历一次不一样的证明. 这为学生的动手操作、实践体验奠定了基础.

2. 巧用“五巧板”證明

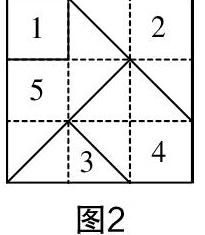
教师为学生提供“五巧板”，让学生在观察、对比、互动中了解五巧板的组成和关系，如图2.

3. 小组合作，智慧碰撞

教师给学生提供两副五巧板，以小组合作为背景，让学生试着拼成一个以c为边长的正方形，再将另外一副拼成两个边长分别为a，b的正方形.

（在这个过程中，学生的分组要合理，要由领队的学生带领团队一起动手动脑. 在关键时刻，教师要随时巡视整个班级的动手操作情况，并适时点拨、启发，让孩子在动手中动脑，在交流中互补，在碰撞中升华，并让学生感受到什么是“青朱出入图”，以此采用“青朱出入图”验证勾股定理）

最终，学生拼出如图3的图形，此时再将a，b，c标出，结合面积关系很快就可以证明a2+b2=c2.

除此之外，我们还可以继续启发学生、点拨学生，引导他们利用五巧板拼图的方法来验证勾股定理.

在这个过程中，学生感受到的不仅仅是一个深入体验、感悟、交流、碰撞的过程，还巧妙地利用以形助数的方法证明了勾股定理. 在这个过程中，虽然我们需要一定的时间来尝试、分析、交流、碰撞，过程中可能存在迷惑和答疑，但是，最终的效果却是深刻的.

4. 达·芬奇验证方法

在接下来的活动中，教师可以采用视频介绍等方式，介绍部分国外经典的勾股定理证明方法，其中最为著名的就是著名画家达·芬奇的方法. 我们可以采用以下环节来引领学生参与和理解：

（1）如图4，在A4纸上画2个边长分别为a，b的正方形，连接BC，FE.

（2）沿ABCDEF剪下，再沿AD剪下，得2个大小相同的纸条.

（3）将其中一块翻转后与另一块拼成其他图形.

（4）比较原多边形ABCDEF和拼成的多边形A′B′C′D′E′F′的面积，你能验证勾股定理吗？

（过程如图5. 教学时可给学生充足的时间进行独立思考，鼓励学生交流合作，教师巡视帮助，引导学习困难的学生. 最后，验证方法，让学生进行讲解、板演、叙述，教师做简单的总结）

到此，学生的体验是深刻的，感触也是深刻的. 学生从中感受到了方法的巧妙性、科学性、多样性，这样的体验充分激活了学生的思维.

■ 课堂总结，感悟文化

前面的学习，我们给学生渗透的不仅是多元的方法与技巧，更让学生感受到了古今中外人类在探索自然奥秘过程中付出的艰辛与智慧，也深刻感受到了我国古代数学家的智慧. 为了激发学生的思维，我们抛出了如下问题，让学生做进一步的交流与讨论.

问题1：通过刚才的体验和交流，你和你的小组有什么新的收获？

问题2：对比上一节课的逆向思维证明方法，你今天是用什么数学方法和数学思想来验证勾股定理的？以前用过类似的方法吗？

问题3：了解了我国古代“青朱出入图”和外国的达·芬奇验证方法，你觉得你更容易想到哪种方法？他们的这些方法有异同点吗？

（提出这些问题后，教师要充分还原学生相互交流、讨论、碰撞的时间和空间，让他们在交流中提升对文化价值的感悟）

任何一门课程都有其特有的文化价值和文化内涵，教师在教学过程中要注重这个环节的挖掘与渗透，真正在学习知识与技能的过程中提升学生的感悟，提升学生的文化素养积淀，真正促进学生综合素养的提升，彰显学科价值的魅力.