结构化,单元整体教学的实践与思考
钱春平


摘 要:文章基于辩证唯物主义联系观,论述如何通过单元整体教学,即用联系的观念整合、完善、优化教材,并引导学生经历比较辨析、归纳整理、聚合发散、融会贯通等深度思维过程,学习整体的结构化数学,让学生自己“织网”,连点成链,织链成网,最终将知识与技能、思想与方法融为一体,感受数学的独特魅力。
关键词:联系观;结构化;单元整体教学
郑毓信教授指出:“基础知识的教学不应求全,而应求联;基本技能的教学不应求全,而应求变。”世界是一个普遍联系着的有机整体,任何事物都不能孤立存在。数学无论是知识本身,还是学习知识的方法都是自成体系的,都是结构化的,都是有机生长的。基于联系观把所学知识连点成线,织线成网,编网为体,发挥整体教学功能,让学生把各部分知识相联系,找出知识的本质和规律,让学生在理解的基础上逐步掌握并运用知识。下面结合实例谈谈笔者如何运用结构化思想指导单元整体教学的实践与思考。
■一、单元固化,用联系的观念整合教材
数学学科本身就具有抽象性、严谨性等特点,尤其在数学课程内容的组织上,其内在逻辑联系十分紧密,环环相扣,前阶段的知识是后面学习的基础,而后阶段的学习也是前面的发展和延伸。用“大数学”的眼光来看,数学课程体系本身就是培养有序思维的重要材料。因此,在教学这样的单元时,可从单元整体教学入手,把知识点用联系的观念适当整合,提升认知间的联结能力。
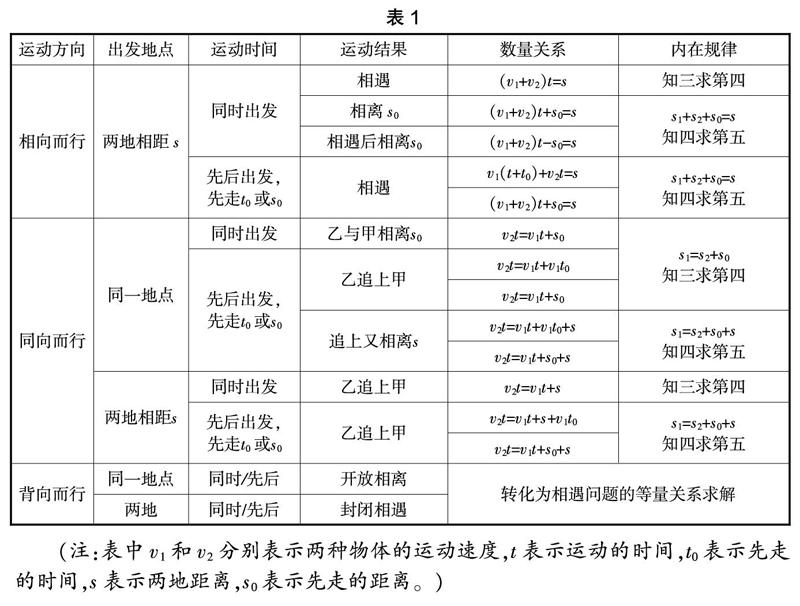
例如,“行程问题”的数量关系运用之所以复杂,是因为“行程问题”有许多变化多端的变式,但是这些变式之间也不是无规律可循的,它们之间其实具有万变不离其宗的内在关系。一般来说,“行程问题”的运动状态可从四大要素来展开研究,即出发地点、运动方向、运动时间和运动结果,其数量关系会随着运动状态的变化而变化。具体地说,“行程问题”根据运动方向可以分为相向而行的问题、背向而行的问题以及同向而行的问题;每类问题按照出发地点和运动时间又可以分为同时不同地、同地不同时和同时同地等情况。其中,相向而行的问题按照运动结果还可以分为相遇、相离、相遇又相离的情况;背向而行的问题按照运动结果可以分为开放相离、封闭相遇的情况(行走路线封闭);同向而行的追及问题按照运动结果可以分为相离、追上、追上又相离的情况。每种情况的数量关系也伴随着运动状况的变化而发生相应的变化。為说明各种运动情况的数量关系,对“行程问题”数量关系之结构进行了简要概括的分析,如下表所示:
当然,由于“工程问题”在某些方面与“行程问题”知识结构有着相似之处,因此我们在系统分析“行程问题”知识结构的同时,也不妨适当将“工程问题”联系起来,无论在基本的数量关系分析时,还是在特殊数量关系分析时,抽象出共性之处,共同分析、共同思考。
不仅让学生理清数量关系,而且通过直观比较,让学生更清楚知识之间的联系和内在规律,便于学生从整体上把握知识结构。
■二、单元扩充,用联系的观念完善教材
在单元整体研读设计中,发现部分教材的编写内容缺失,前后联系即教学体系缺乏。因此,在单元整体教学时,在“联系观”指导下,在原有知识体系基础上,延伸出教学内容的联结点、生长点,对部分单元教学内容进行扩充教学,使教学材料的结构更加有序和丰满。
例如,四年级下册“平均数与条形统计图”单元的体系跨度太大,不扩充对学生知识体系的建立有较大的困难。
四年级上册条形统计图的教学编排结构如下:
本单元教材具体编排结构如下:
不难看出,下册“平均数与条形统计图”中出现了复式条形统计图的教学,但是在后续的练习中却又出现了带有特殊起始格的条形统计图的练习题(图4)。
带有特殊起始格的条形统计图在日常生活中的应用广泛。如果不进行补充教学,让学生明确为什么这一格需要压缩,那么学生对于改制试点的理解和运用会有缺陷。因此,在教学复式条形统计图前安排了教学“带有特殊起始格的条形统计图”一课,让学生明白在制作条形统计图时,需要清楚地看出各类数据的多少,有时根据需要可以把起始格进行压缩。这样既能清楚地看出各类数据的多少,又能让条形统计图美观,不至于画得过长或差距微弱,看不出数量的多少。扩充完善后的单元具体编排如下图:
■三、单元重组,用联系的观念优化教材
在联系观下,单元整体研读时,发现部分单元教材的课时编排顺序有所欠缺,使得每个知识点之间的逻辑联系不够紧密,影响了教学中学生的语言表达和思维的跟进。因此,根据需要把部分单元进行单元重组也是整体研读的重要探索方式。如四年级下册“三角形”单元原来的编排顺序如下:
这样的编排,让教师们在教学第一课时的三角形的高时“犹抱琵琶半遮面”。四年级学生虽然没有正式学习过三角形的分类和直角三角形的各部分名称,但是课外接触过不少。如果按原编排教学,首先学生会在课堂中随时出现这些名称,教师要不断地引导,费时费力,不能突出重点;其次在探索“三角形有三条高”这个知识点时,如果不明确上述知识点,探究得牵强,后续再去教学三角形的分类就感觉分类的目标单一,也影响了学生对于钝角三角形和直角三角形其中两条特殊的高的深刻认识。因此,基于联系观,运用结构化教学思想进行单元重组,具体安排如下:
这样的大动干戈让知识点之间的逻辑联系更加紧密,更方便学生理解,在教学时,一个实验班按以上编排教学,学生思维的活跃度和对知识点的认可度都达到了一定的高度。可见,在教学中对可以整合的一些环节进行大胆的整合、重组,让教师比较着教、联系着教,在讨论中教,在争辩中教,使教学拥有更大的空间,使教学走向开放,走向“板块”。
基于“结构化”的单元整体教学实践探索,让我们对知识结构、方法结构、过程结构等系统观概念有了深入的认识与理解,而且有利于教师形成整体的综合的大数学思维方式。对于学生而言,不仅有利于学生形成结构化的认知,而且还有利于学生在潜移默化中形成结构化的思维方式,学生的学习也更加系统、更加逻辑,有了数学结构的支撑而更富生命力。结构化教学是一种行走方式,是一种向上姿态,是一种生命拔节。把学习过程拉长一些,拓宽一些,丰满一些,让学生所学知识相互联系,形成结构,生成体系,学生的学习过程才能深入,知识的建构才能深刻,能力提升才能明显。基于结构化的单元整体教学——从学的视角重构数学课堂,将是我们教学之路走上永恒的话题,也是我们追寻的目标。将数学学习过程全力放大,聚焦本质,让学生深刻经历学习的过程,获得知识与技能,感知知识背后更有价值的东西——知识的由来与演变,知识的逻辑与结构,数学的思想与方法,活动的体验与感受,等等。

