基于分层模糊符号有向图的故障诊断方法研究综述

付 宇 崔玉福 李志刚 刘元默

(航天东方红卫星有限公司 北京 100094)

引言

目前小卫星故障诊断以安全模式设计、地面飞行控制监视为主,事先将指令存储待相应事件触发再调用。小卫星在轨飞行过程中,地面飞控人员开展数据监视和处置工作,根据小卫星飞行状态和任务下达指令;遇到紧急故障引导小卫星进入相应的安全模式[1]。这种故障诊断的原理是将实时数据与事先设置好的大范围阈值进行比较,若超限则认为故障发生,设置的阈值不能根据实时工作阶段进行调整,因此会造成一定的误判或漏判,诊断精度不高。

随着小卫星在轨运行长期化、任务多样化和结构复杂化,对于小卫星的故障诊断能力也提出了更高的要求。主要体现在：①提高实时性。目前的故障诊断方法不能根据实时状态对阈值进行调整,因此实时性必然不高。②提高多元报警时的故障诊断能力。小卫星结构日益复杂,故障诊断不应只局限于处理单个节点报警,在多元报警时能够推理出最根本的故障源,并为故障隔离提供顺序,才是更亟需的诊断方法。

就航天器的故障诊断方法而言,大体可分为两类,一是与模型无关的方法,检测故障的参数设置较简单,目前应用较多,但需要大量历史经验作为样本训练,不适合于小卫星系统;二是基于模型的方法,无需经验数据作为基础,根据建模方法的不同可分为基于定量模型和基于定性模型。定量模型法以建立精确模型为基础,适用于线性系统和有解析模型的系统;定性模型法适用于参数关系复杂,无法得到数学模型的大型系统,通过分析内部逻辑关系实现建模,又包含符号有向图法、定性物理法和综合诊断引擎法。

小卫星的电源分系统主要承担在轨运行过程中所有负载的供电,对飞行任务的完成与否起着重要的作用,一旦出现故障,将直接导致其他分系统的正常工作以及飞行寿命。不仅如此,据研究表明电源系统的在轨故障概率在所有分系统中比例最高[2]。小卫星电源系统内变量繁多,难以建立数学模型,只能由实验数据得到趋势分析,因此更适合于定性模型法。但单一的定性模型也存在故障搜索空间大、多元报警时无法得到故障隔离顺序等局限性,所以本文将选择定性模型法中适合小卫星电源系统的一种方法进行改进,实现故障模型建立和诊断推理优化。

在轨运行的特殊性使得小卫星必须具有一定自主性,实时的故障诊断可以确保小卫星活动的安全可靠。总的来说,在轨运行具有以下特点[3]：①太空环境特殊,不确定性因素多。小卫星运行于太空经常受到高低温真空环境的剥蚀、空间碎片的撞击、空间粒子的辐射、电磁干扰等不确定性因素的影响,元器件的故障概率也随之大大增加。②星上资源有限：星载计算机的存储空间、星上传感器的数量和小卫星能源储备等均受到限制。③故障历史样本少,诊断经验不足。同一批次的产品数量不多且测试和检测次数有限,为故障诊断的提供参考的历史知识少。

由于上述特性,一旦在轨故障,必将导致较严重的后果。2010年2月,“遥感八号”遥控终端和GPS发生单粒子翻转造成单机异常;2011年4月,先进陆地观测一号卫星的电源系统突发异常,迫使卫星进入安全模式,有效载荷全部关闭;2012年2月,SES-4卫星的太阳电池阵无法展开,无法为飞行任务供能;2013年5月,GOES-13卫星的姿态轨道控制系统故障,不能再为地面传输气象数据[4]。

因此,只有优化故障诊断方法才能加强小卫星在轨故障后的自我处理能力,在地面飞控人员无法实时处理情形下自主快速定位故障源,实施故障隔离,挽回损失。

1 故障诊断方法研究综述

首先为小卫星电源系统选择适合的故障诊断方法,再对其改进。根据是否需要建模以及模型的类别,对所有故障诊断方法分类,如图1。

图1 故障诊断方法的分类

1.1 与模型无关的故障诊断方法

分为信号分析法和基于知识法。

(1)信号分析法主要是传统的主元分析法和基于小波变换法;都具有诊断速度快,灵敏度较高的优势,适合于线性系统。但受噪声等外界干扰的影响严重,诊断精度较差;诊断系统往往局限于单一故障[5];诊断结果可能受到主观性的影响,不具有客观性。

(2)基于知识的诊断方法主要包括故障树法[6-8]、基于模糊逻辑法[9];故障树法的优点是直观、形象,可以根据传播路径从而分析故障原因;知识库可以根据经验修改。缺点在于诊断结果严重依赖故障树的正确性和完整性,如果根据知识写出的故障树不完整也将导致诊断结果不准确;基于模糊逻辑法必须构造隶属函数,但不允许在构建过程中存在未知因素,同时,隶属函数具有一定的主观性也将影响诊断精度。

因此在与模型无关的方法中,基于知识的方法相比信号分析法的诊断精度更高,受噪声影响较少,具有自适应、自学习的能力;但这类方法需要大量历史数据,对历史数据较少的小卫星而言并不适合,因此基于模型的方法成为小卫星故障诊断的首选。

1.2 基于模型的故障诊断方法

根据系统建模方式不同,这类方法分为定量模型法和定性模型法。

(1)定量模型法

用数学模型的形式来表述系统,基本思路是通过实际获取的系统输出与数学模型的理论输出分析得到残差信号,从而实现故障诊断,核心是用解析冗余代替硬件冗余[10]。

优点是可以充分利用系统的深层知识,及时检测到故障的发生,相比与模型无关的故障诊断,它的优势在于能够克服小卫星故障诊断中存在的历史经验少、信息不充分的难题。但实际应用中,部分小卫星的分系统还难以用解析模型描述,如小卫星电源系统的蓄电池组存在的在轨衰减情况。

(2)定性模型法

核心是由定性观测结果辨识出系统的状态。基于定性模型的方法主要有：因果图法、定性物理法和综合诊断引擎法。

基于定性模型的方法通过元件之间的因果关系离散地描述系统,不需要建立精确数学模型,不需要精确地数学计算和求解,通过局部传播就能实现系统的行为预测和行为解释,具有更高的故障推理能力,是从较高层次上给出系统的宏观描述,适用于航天器推进系统、电源系统。

1.3 基于模型的故障诊断方法

通过研究故障诊断几种方法的思想和实现流程,将它们的优缺点和适用范围归纳如下图。

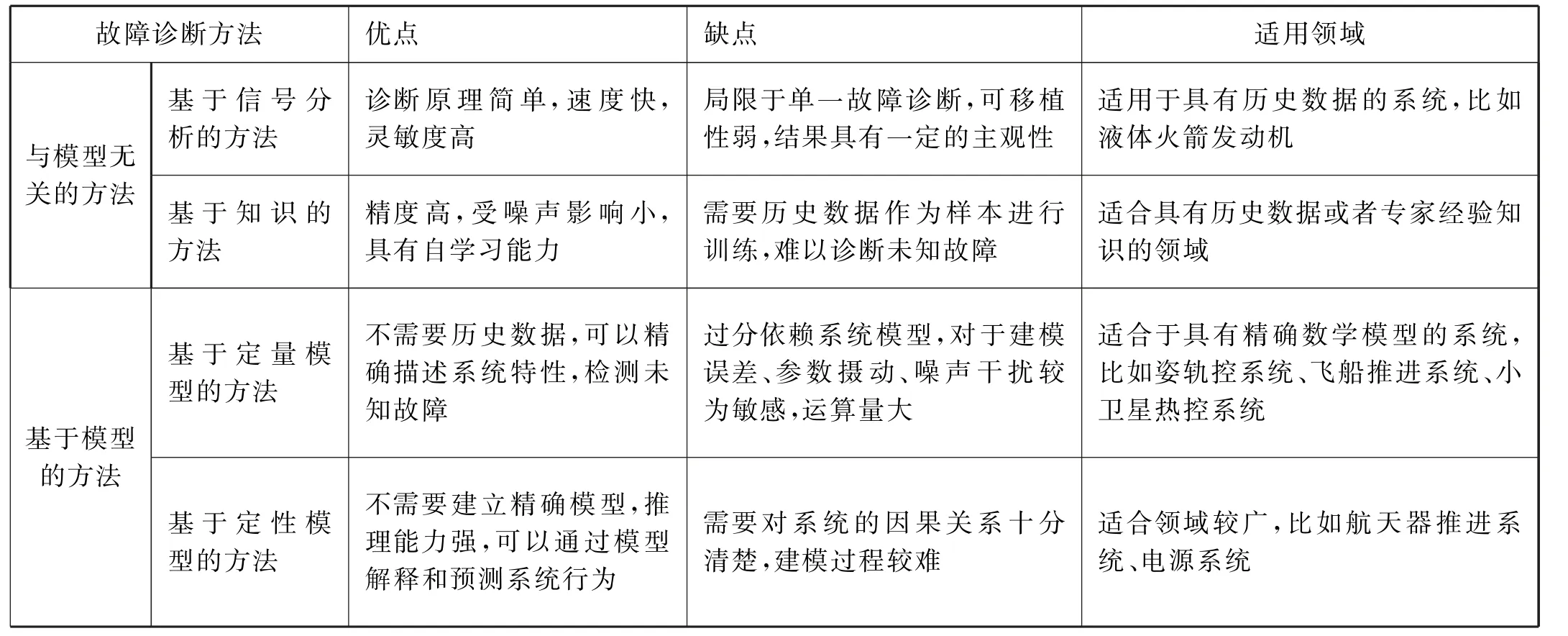
表1 故障诊断方法优缺点对比

总的来说,与模型无关的方法诊断知识的表示简单、直观,推理速度快,但因需要大量历史经验而存在数据获取瓶颈问题,推理方式与策略不灵活,难以诊断未知故障,不具备推理能力。

基于模型的方法都不需要历史知识,其中基于定量模型的方法是通过代数方程、微分方程等精确的数学形式描述系统,但过分依赖系统模型,对于误差和噪声等外界干扰较为敏感;且由于系统行为分析需要人来完成才可以实现建模,因此对复杂度高、非线性的系统无法完成,适合于具有精确数学模型的系统,比如姿轨控系统、飞船推进系统、小卫星热控系统。而基于定性模型的故障诊断方法通过元件之间的因果关系离散地描述系统,不需要建立精确数学模型,不需要精确地数学计算和求解,通过局部传播就能实现系统的行为预测和行为解释,具有更高的故障推理能力,是从较高层次上给出系统的宏观描述,适用于航天器推进系统、电源系统。

1.4 国内外研究现状

从20世纪60年代开始,在航天器故障诊断技术方面,国外以美国、日本、西欧为代表也开展了大量的探索。从无到有、从落后到先进,主要经历了以下几个阶段：

(1)20世纪60-70年代的阈值诊断：受技术限制,这一阶段的诊断方法仅以单信号处理方法为主。比如美国水星号航天器采用参数阈值监测、地面专家会诊方法。

(2)20世纪70-80年代初的算法诊断：算法水平的提高使故障诊断方法由单信号处理向多信号滤波诊断发展。例如,阿波罗飞船建立的飞行异常分析及评价系统可以独立自主地保障其安全运行。

(3)20世纪80-90年代的基于知识的诊断：随着人工智能领域蓬勃发展,基于知识的诊断技术逐渐被应用于航天器,尤其是故障诊断专家系统原型的开发。

(4)20世纪90年代以来开始出现了基于观测器的定量模型法和基于因果图的定性模型法。

20世纪80年代开始,我国也加入航天器故障诊断的研究浪潮之中,各大学、研究机构相继针对不同对象开展了不同诊断方法的研究。中国空间技术研究院总体部建立了卫星故障数据库,涉及到总体部研制或抓总研制的所有卫星分系统和200多种单机,故障案例信息600余条,包含国外卫星和总体部产品故障两部分;沈阳航空航天大学对1993-2012年间国内外300多次航天器在轨故障案例进行整理,发现各分系统中电源、控制、结构机构分系统的故障比例较高;1999年,刘冰等利用工具CLIPS针对YF-75发动机提出了一种故障诊断专家系统;2002年,张纯良等对神舟飞船的推进分系统应用键合图法开展了故障诊断研究;2004年,张庆振、李清东等针对运载火箭的故障检测处理系统设计了一种专家系统;2006年,刘发金等对姿态轨道控制分系统研制了神经网络的诊断专家系统;2007年,夏勇等针对运载火箭提出了以故障树法为基础的专家系统;2011年,岑朝辉等提出了卫星姿态轨道控制系统实时信号的基于神经网络的故障诊断方法。502所针对控制分系统的敏感器、执行器等设备,提出了基于观测器、故障检测滤波器等方法的故障诊断研究。

应用方面,502所针对卫星在轨飞行状态及控制分系统故障监视提出了专家系统原型;航天东方红卫星有限公司的小卫星自主故障处理主要采取基于安全模式设计的方法,对某些重点遥测参数设计安全门限,星务分系统对通过星上总线采集回来的遥测参数进行分析,与相应门限值进行比较,若超出门限则认为故障发生,自主执行预定的安全指令序列,如执行切机、切总线、关载荷设备等操作,属于安全性导向设计,卫星收集各分系统的安全状态信息,并根据事先设置的控制策略对影响整星安全的关键设备进行控制管理,保证整星的安全。

2 符号有向图

2.1 几个重要概念

符号有向图模型(Signed Directed Graph,SDG)这一定性模型将系统内部关键变量间的因果关系直观地表述,使其在化工领域的安全评估和故障诊断的应用中取得了巨大进展。

文献将符号有向图相关概念定义如下：

定义1：SDG 模型GS是由有向图G 与函数φ组成的。

其中,(1)有向图G 由两部分组成：

V={vi}包含系统所有节点的状态,E={eij}包含节点之间所有有向边;

(2)函数φ 代表节点间的影响关系,表示为有向边eij的符号：

定义2：δ(vi)∈ { + ,-,0},即

其中,Xvi代表某一变量的实时数据,为正常工况的上下限。

图2-1所示为一个简单的SDG 模型,有三个节点A、B、C。A 的实时状态超过了常态工况,“+”,B 正常工作,因此节点符号是“0”,C 的此时工作值比正常工况最小值低,为“-”,A、B之间的箭头由A 指向B,代表A 对B有影响,且因为是实线所以A 对B有正影响关系。A、C 之间的箭头由A 指向C,代表A 对C有影响作用,虚线代表A 对C是负影响关系。

图2 SDG 模型示意图

2.2 研究现状

自1974年以来,基于图论的故障诊断方法在工业系统中得到了广泛地应用与研究。学者Nakann与Nakannishi是最早使用此方法的专家,但只局于部分问题的应用;1977年研究人员G.J.Powers与S.A.Lapp在研究中首次构建了符号有向图模型,但没有给出定义;1981年,Iri M.等提出了符号图的概念,并应用于单一故障源的情形;同年,T.Umeda等依据各个节点之间影响关系提出了多级SDG 模型;1985年,J.Shiozaki等将Iri M.的符号图概念重新表述为符号有向图,同时提出新的符号有向图模型(节点存在五种状态)与基于此模型的新方法,应用于实验,实验结果显示新模型的建立使诊断的准确性提高;1987年,M.A.Kramer等找到了用于揭示深层次影响关系的专家系统规则,并在工业大规模系统中应用。

在符号有向图法提出后的十多年中,研究主要围绕纯定性模型展开,但由于自身诊断精度不高、效率较低的缺陷,从1990年开始,专家学者通过引入先进技术、结合最新算法的手段对符号有向图法进行改进,如：模糊集合理论、定性趋势分析、主元分析方法、小波分析等。

对符号有向图模型的研究,国内起步虽晚但发展迅猛。1996-1997年,国防科技大学的朱恒伟等提出为火箭发动机搭建静态仿真模块,用模糊隶属度描述静态的故障严重程度;2002年,浙江大学的王勉宇提出通过分层对符号有向图模型进行优化;2005年-2006年,清华大学的扬帆、萧德云通过建立结构残差应用于故障的分离与检测中,提高了系统的鲁棒性与精确度;2006年,华北电力大学的曹文亮、王兵树等将符号有向图应用于热力系统,对高加给水加热装置搭建模型,采用模式识别对系统构建故障知识库,结合主元分析方法解决节点阈值的确定问题;2007年,晏政等将符合有向图法应用于航天器推进分析图实现了故障诊断;2008年-2009年,宋其江、徐敏强、王日新等结合定性趋势分析对符号有向图模型进行优化;2003年-2010年,北京化工大学的张贝克教授团队针对石油化工行业发明了HAZOP计算机软件,在符号有向图模型中结合HAZOP构建了分析综合平台,实现了模型的构建、故障诊断与在线数据分析评估等功能。

3 分层结构

3.1 研究现状

21世纪初,印度学者P.Gandhi与R.Sehgal等依据故障传播方向总是由有向图模型的高层指向低层的特性,设计了分层算法。经过对机械领域的应用验证,通过建模与数据处理,显示分层算法使系统具有更好的层次结构、诊断效率提高。

国内部分学者也针对分层模型做了理论或应用研究。哈尔滨工业大学首先对分层有向图模型做了严格的数学定义,通过对其在热力发电、航天器等领域的应用,验证该模型具有诊断精度高、诊断高效的优点;太原理工大学的杨蕊也在论文中针对符号有向图法在发电系统存在的诊断效率低的问题,提出分层概率符号有向图模型的改进手段,实现了对大规模复杂系统的优化诊断。

3.2 重要矩阵

在符号有向图模型中支路为带箭头指向的有向边,箭头所指方向与故障传播方向一致,从最高层节点向低层节点传播,由此建立了分层算法,解决传统符号有向图模型的搜索空间较大缺陷。通过分层将SDG 模型转化为分层SDG 模型。当有节点异常并发出警报后,根据报警点所在模型中层次,只将最高层报警点纳入备选故障源进行诊断推理,有效缩小搜索空间,提高诊断的效率。

在计算机中,通常用邻接矩阵和可达矩阵的形式来描述有向图中节点与节点的指向关系等信息。以下为这两种矩阵的数学定义。

定义3：用邻接矩阵可以将有向图G=(V,E)用数学形式表示出来,体现两个节点之间的直接影响关系,即是否存在有向边。

定义4：用可达矩阵可以表示有向图中节点间的间接影响关系,即一个节点是否可通过若干节点及之间的有向边最终与另一节点相互影响。

下面举例说明有向图两种矩阵的对应关系,如图3。

图3 包含4个节点的有向图

此有向图中包含的节点较少,可以分别对每个节点进行观察,从而直接得出有向图对应的可达矩阵,节点1通过有向箭头分别可以到达节点2和4,因为能够到达即在行标为节点l,列表为2、4的这些位置上赋值“1”;节点2通过箭头可以到达节点4,所以行标为2,列标为4的元素为“1”;节点3能通过箭头到达节点1、2、4,所以行标为3 列标为1、2、4 的元素均为“1”。所以得到有向图的可达矩阵P4×4如下所示：

3.3 分层算法

通过分层算法计算有：

先对有向图的邻接矩阵A 进行分层判断,判定系统可以分层。再求每一层节点。

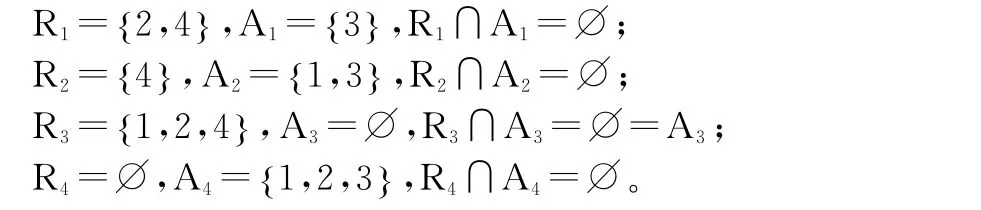
所以第一层只包含一个节点即节点3。去除节点3所在行列,得到新的可达矩阵P2

所以第二层的节点是节点1。继续去除节点1所在行列,得可达矩阵P3

所以第三层是节点2,第四层是节点4。由此可得系统的分层有向图为

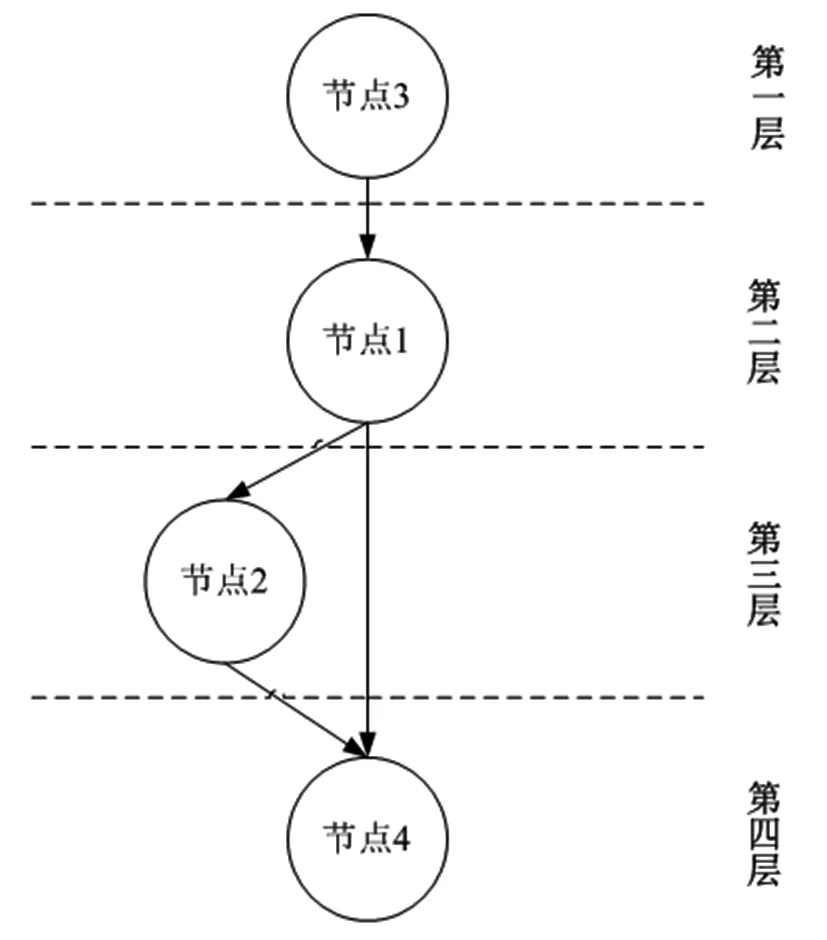
图4 包含四个节点的分层有向图

分层算法处理过的模型具有分层结构,表述了系统节点所在层次。经分层处理的系统,其实是按原因、结果关系将系统分层,即高层节点为原因,低层节点为结果。在进行备选故障源推理时,只对报警节点中的最高层进行反溯,且将反溯过程中得到的有效节点中与最高报警点比较,若为同层或更高层则纳入备选故障源集合。

4 隶属度函数

分层符号有向图模型虽然层次性好,判断故障的来源更加有条理,但是由于忽略了定量信息的应用,所以仍存在只能给出备选故障源节点的集合,而无法给出故障源发生故障的可能性的严重缺陷,严重影响着诊断的精度。

定义5：μ为模糊隶属度函数分布,μ( vi)∈[0,1 ],满足如下关系式：

其中,vipInferior,vinInferior分别表示节点vi常态的正、负阈值,vipSuperior,vinSuperior代表节点vi的正、负报警阈值。

也就是说当节点的实测值大于警报阈值上限或者小于警报阈值下限时,隶属度为1,节点报警,显示为故障;当实测值在正常工作范围内,隶属度为0,显示为正常;实测值位于两者之间时,不可知是否发生故障,可以用斜率来计算此时的隶属度。

图5 隶属度函数

如果已知系统故障瞬时数据,按以下步骤求得各节点模糊隶属度：

(1)根据节点的工作特性给出正常工作范围和警报阈值范围,画出该变量的隶属度函数;

(2)将节点的故障瞬时数值在隶属度函数中标出;

(3)根据故障数据所处位置,选择隶属度对应公式,求解;

(4)完成参数的隶属度列表。

对于分层符号有向图模型而言,加上每个节点的隶属度数值,就可以得到最终的分层模糊符号有向图模型。

5 故障诊断流程

定义7：节点符号δ (vi)≠0,可称节点有效;当δ (vi)φ(eij)δ(vj)=+,此支路eij就为相容通路。

因为故障的传播是只能通过相容通路才能进行的,根据这一规则可以在故障诊断中缩小搜索范围。对系统中每一个有效节点都进行相容通路的判定,得到系统所有的相容通路。

而备选故障源集合C 的确定：

(1)当节点报警时,根据模型找出位于最高层的报警点,若存在若干报警节点同层,则给出最高报警节点集合T={vi}。

(2)从T 中任取出一个节点vi,从该节点沿相容通路反向回溯,初步得到备选故障源。(依据相容通路的规则筛选故障源)

(3)在备选故障源中再次筛选,只保留与最高层报警点同层和更高层的节点(依据分层模型的规则筛选)。

得到集合C 之后,再通过故障诊断算法求出备选故障源是真正故障源的可能性排序,具体步骤如下：

(1)计算C 中每一个故障源节点的每一条相容通路支持度μlx-support。

设节点vi有若干相容通路,它的相容通路支持度等于除了vi以外其余k 个节点的隶属度的最小值,即μl1-support=min;同理可以求得节点vi其他相容通路支持度μl2-support,μl3-support,…μlx-support。再求C 中其余节点的相容通路支持度。

(2)对C 中每一个节点,求支持强度μvi-support,即这一节点的所有相容通路支持其为真正故障源的可能性。

对于节点vi支持强度是所有相容通路支持度的最大值,即

(3)计算每一个C 中节点的模糊支持度μi,即该节点为真正故障源的可能性。

对于节点vi,它的模糊支持度等于隶属度和支持强度的最大值,即μi=max( μvi-support,μ( v1)) 。μi越大则可能性越高,如果μi太小,可以设置一个阈值ε∈[0,1 ],当μi＜ε,就将该节点从集合C 中删掉。

6 小结

通过对故障诊断方法的研究及优缺点对比,认为不需要建立精确数学模型和进行数学计算的定性模型法,具有更高的故障推理能力,可以从较高层次上给出系统的宏观描述。选择定性模型法中的符号有向图法并进行改进,引入分层结构和隶属度函数,并给出了改进的故障诊断技术的诊断流程。符号有向图法的重点在于梳理清楚系统内各主要变量的逻辑关系建立符号有向图模型;将分层模型引入建模过程,可以有效排除一些不可能的故障源节点,缩小搜索空间;增添隶属度定量信息可以更精确地描述故障情况。再根据相容通路回溯、结合故障模型可以在多元报警情况下快速排除低层次节点、得到真正的故障源。