海啸俘获波在弯曲海脊上的传播规律

于洪荃，胡见，王岗,3*，张尧，郑金海,3

( 1. 河海大学 海岸灾害及防护教育部重点实验室，江苏 南京 210098；2. 长江航运发展研究中心，湖北 武汉 430014；3. 河海大学 港口海岸与近海工程学院，江苏 南京 210098；4. 自然资源部海洋减灾中心，北京 100194)

1 引言

海啸是一种由海底地震、海底滑坡、火山爆发等所引发的破坏性海浪。海啸相对于受灾体可分为从较远距离传播而至的越洋海啸和距海啸发生地较近的局地海啸[1]。其中在相对开阔海域发生的较大海啸多数为越洋海啸。如2006 年千岛群岛海啸传播至美国新奥尔良并给该地区带来灾害影响[2]；2011 年日本东京海啸不仅在日本沿岸引发最大38.9 m 的爬高，还穿越整个太平洋最后抵达智利[3]。大量研究表明越洋海啸受到大洋海脊的引导以俘获波的形式影响至较远区域[4-6]。

海脊俘获波的研究最早可追溯至Jones[7]于1952年从数学上给出了顶部淹没的无限长海脊俘获波理论。此后，Longuet-Higgins[8]给出了无限长矩形剖面海脊的解析解。Buchwald[9]建立了一个两侧水深不相等的矩形海脊模型，证明了俘获波在这种条件下会有无限多个传播模式，并给出了大西洋海脊的数值频散曲线。考虑到实际海脊地形是连续的，Shaw 和Neu[10]给出了三角形剖面海脊的俘获波理论，Zheng等[11]则给出了抛物型海脊俘获波的解析表达，王岗等[12]将夏威夷海脊的剖面地形拟合为双曲余弦函数，并给出了该地形上的俘获波解析理论。最近，万鹏等[13]基于射线理论推导了指数型海脊上波浪传播轨迹的理论解，并提出了震源位于海脊顶部的海啸被海脊完全俘获的条件。

大洋海脊上的俘获波现象在历次越洋海啸传播过程中也得到了证实[2,14-15]。日本和智利分别位于太平洋的西北角和东南角，相距1.7 万km 以上，但是日本发生较大海啸时往往跨越整个太平洋给智利造成严重灾害（如2011 年的东京海啸[3]），而智利发生较大海啸时同样也会给日本带来巨大的影响（如2010 年的智利大海啸[16]）。导致这一现象的原因是，日本-智利沿途存在许多如夏威夷群岛等岛链和海山群所构成的海脊系统，海啸在这一特殊地形影响下能量聚集并沿其传播，对太平洋的另一端造成灾害影响。1996年Irian Jaya 地震产生的海啸，虽然该地距离日本较远，但却对日本沿海地区造成较大影响。Koshimura等[17]采用基于线性长波理论的数值模型反演了该次海啸，发现由于Mariana 和South-Honshu 海脊的引导作用，使得海啸波能够具有较大能量传至日本。

全球海脊的分布复杂多样、蜿蜒曲折，局部甚至出现超过45°的转角。俘获波在这类弯曲海脊上是否仍能继续以俘获波形态继续传播，在经过弯曲段有多少能量继续沿海脊传播、又有多少能量泄露出海脊，还未有研究阐述。这对于到达远场地区的越洋海啸的最大波高预测具有重要意义。本文将基于数值模型试验，研究俘获波在两段不同角度连接的双曲余弦海脊上传播过程，并与王岗等[12]所提解析理论比较，确定俘获波在不同弯曲角度的海脊上的能量俘获与泄漏关系。

2 数值模拟

本文所采用的模型为丹麦DHI 公司研发的MIKE21-BW 模型。该模型基于Madsen 等[18-19]提出的扩展型Boussinesq 方程，能够适应相对水深h/L＜0.50 的水域。海脊剖面为对称的双曲余弦形式[12]：

式中，λ是决定海脊形状的参数；2L是海脊的宽度；h0表示海脊顶部的水深；h1=h0·cosh2（λL）表示平底处海底的水深。

海脊的尺度参照夏威夷海脊[20]，参数λ=9×10-5m-1，海脊宽度2L=60 km，脊顶水深h0=-80 m，海脊两侧平底水深h1=-4 500 m。图1 给出了模型模拟的平面范围，其中α表示海脊的弯曲角度，其取值范围从0°到90°每隔10°取一组，共有10 组。模拟范围为：0≤x≤1 446 km，0≤y≤2 820 km；直海脊段位于66 km≤x≤126 km、0≤y≤1 500 km 之间，海脊在y=1 500 km 处开始转弯。模型空间上为均匀网格，Δx=Δy=600 m，时间步长dt=1 s，模拟总时长为2 700 min。在0＜x≤60 km、1 386 km＜x≤1 446 km、2 760 km＜y≤2 820 km 范围内各布置100 个网格的数值海绵层模拟无反射边界条件。由于地震发生错动的过程是一个很短的冲击过程，本文忽略断层破裂的复杂性、错位的多样性、破裂厚度可变性等各种因素的影响，基于Okada[21]假设将海底位移等效为初始海面位移。初始水面隆起采用高斯型：

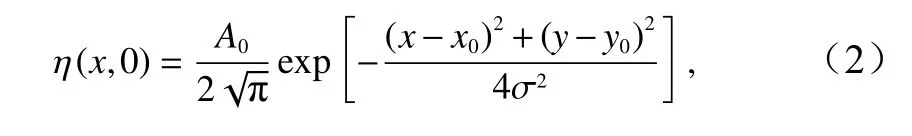
式中，隆起顶点位于x0=96 km，y0=0 处，参数σ=3 000，取此时最高水面点为3 m。由于高斯型水面隆起关于x轴对称，而x轴为全反射条件，因此仅需研究海啸沿y轴的正方向海脊传播的情况。

3 结果分析

3.1 波面过程

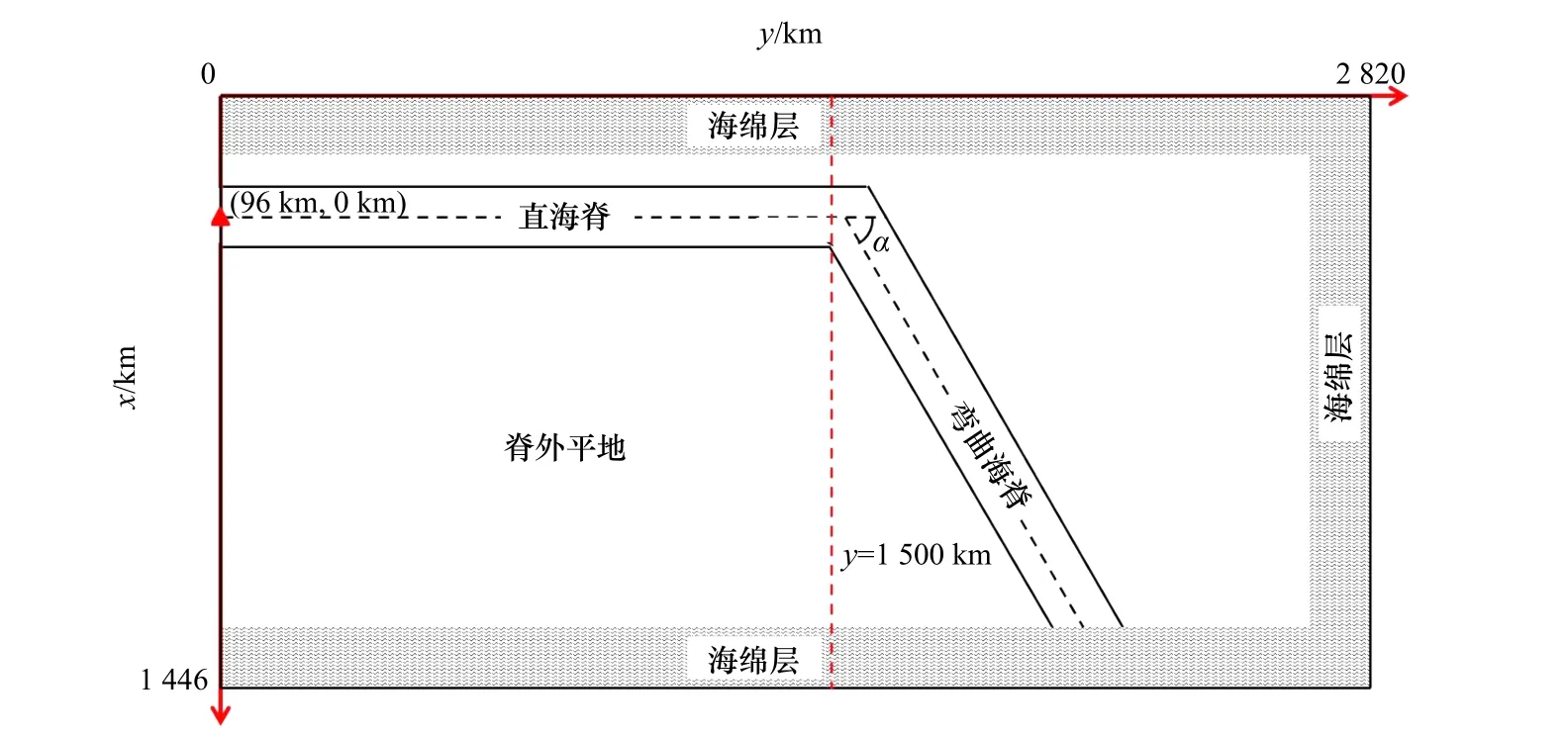
图 1 模型区域示意图Fig. 1 Sketch of the numerical simulation

图2a 给出了30°弯曲海脊上海啸波生成之后不同时刻自由水面的瞬时状态。在t=100 min 的瞬时波面中仍可以观察到传播速度较快的自由波；在t=840 min 时可以发现海啸波的大部分能量以速度较慢、主要聚集在海脊上的俘获波沿海脊传播，且俘获波最大波高出现在脊顶处并向海脊两侧递减；在t=1 020 min 时为俘获波在海脊转弯处的传播情况，大部分俘获波仍沿海脊传播，少部分泄露出海脊以圆弧的形式向外扩散；在t=1 500 min 与t=1 800 min 的瞬时波面图中，俘获波依然以稳定的海脊俘获波的形式沿海脊向前传播，除前几个波高外，最大波高仍出现在脊顶处并向两侧递减，且在同一剖面上、不同水深处的俘获波会以相同的速度前行。而由于波浪具有频散性，俘获波的波群随着海脊方向逐渐增长，同时波的个数逐渐增加、波高逐渐减小。为了进一步说明俘获波在海脊转弯处的反射现象，图2b 同时给出了90°弯曲海脊上自由水面的瞬时状态，在t=1 500 min与t=1 800 min 的瞬时波面图中，除了弯曲海脊段上继续被俘获的海啸波外，在直海脊段上还明显出现了在海脊转弯处被反射回来的沿y轴负方向传播的俘获波。本文3.2 小节将对这部分能量进行统计分析。

图 2 30°（a）和90°（b）弯曲海脊在t=100 min、840 min、1 020 min、1 500 min、1 800 min 时刻的瞬时波面Fig. 2 Snapshots of free surface over the ocean ridge of 30°(a) and 90°(b) at t=100 min, 840 min, 1 020 min, 1 500 min and 1 800 min respectively

图3 是弯曲角度为30°的弯曲海脊脊顶不同位置处的波面过程及其对应的小波谱。海啸波的主要频率f集中在[0.000 3 Hz，0.003 Hz]范围内。小波谱图中的能量明显分为传播较快的自由先驱波和海脊俘获波两部分。自由先驱波传播速度较快，且到达海脊不同位置的时刻相差不大，但因为频散作用导致其在海脊后段的波高减小，因此在对应的小波谱中几乎观察不到。海脊俘获波的能量主要是由以相同速度、不同频率传播的具有孤立波特性的波浪成分和能量主要集中在固定频率范围内的波浪成分组成。

由海啸在海脊上的传播过程可知，海啸波的最大波高为海脊俘获波，本文取频率为0.000 6 Hz，将王岗等[12]提出的解析理论与数值模拟结果中不同海脊横截面上的最大波高对比（图4）。数值模拟结果与解析理论的0 模态可以较好吻合。直海脊段300 km 与900 km 处的波形完全关于脊顶对称，直海脊段1 500 km处的波形由于受到海脊在转弯处反射回来的俘获波影响而不完全对称，弯曲海脊600 km 和1 200 km 处因为俘获波在海脊转弯处传播过的路程不同而导致波形也有些许的不对称。

3.2 不同弯曲海脊能量分析

由于俘获波的最大波高位于海脊脊顶并向两侧减小，因此本文选取海脊脊顶位置的波面过程分析不同波浪成份能量变化。统计的能量主要分为4 类：俘获波初始能量、海脊转弯处反射回来沿y轴负方向传播的能量、经过转弯处继续被海脊俘获的能量和泄露的能量。波能采用线性波理论求得，其中Hi为沿海脊剖面不同位置处的波高。本文每个截面共提取n=13 个位置处波面过程，分别统计不同弯曲角度的海脊上后3 种能量占俘获波初始能量的百分比。

海啸波产生后，沿直海脊经过900 km 的传播后趋于稳定，且此时未受到海脊转弯处反射回来的海啸波的影响，因此选该处为俘获波的初始能量；直海脊1 200～1 500 km 段的能量为海脊俘获波与海脊转弯处反射回来的俘获波叠加的能量，随着反射波在直海脊上的继续传播，由于波浪的频散效应，入射波群与反射波群逐渐清晰分离，此时海脊俘获波群与反射的俘获波群之间有较明显的时间间隔，因此本文选取直海脊600 km 处统计弯曲海脊反射回来的能量；考虑到弯曲海脊600 km 处俘获波经过海脊转角继续传播的能量趋于稳定，故选取该处统计继续俘获的能量。

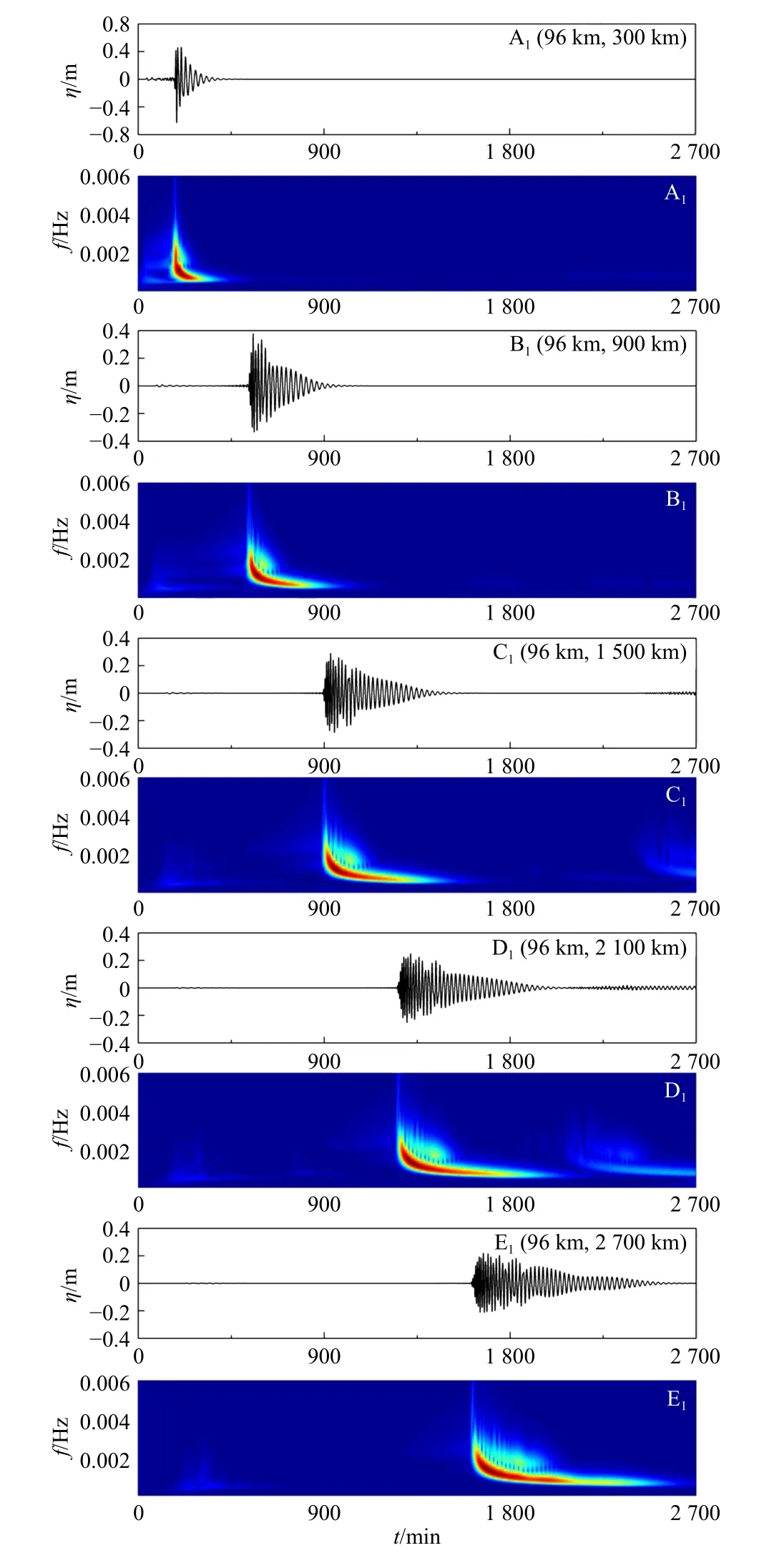
图 3 30°弯曲海脊不同脊顶位置处波面过程及其对应的小波谱Fig. 3 Free surface elevations and their corresponding wavelet spectra over ocean ridge of 30° at different top positions

图 4 30°弯曲海脊上的俘获波剖面模拟结果与模态m=0 的俘获波解析解比较Fig. 4 Comparison of the wave amplitude profiles over ocean ridge of 30° for mode m=0 between the numerical results and the analytical solutions

图5 为不同弯曲角度的海脊上俘获波能量变化。由图可知弯曲海脊上继续俘获的海啸波能量随弯曲角度的增加而减少，且减小的速度越来越快；泄漏出海脊的俘获波能量和反射回来沿y轴负方向继续传播的俘获波能量随弯曲角度的增加而增加。当海脊弯曲角度小于等于60°时，约66%以上的能量可以被继续俘获，1%左右以下的能量被反射回来，其他的能量泄露出海脊。在实际越洋海啸中，我们对于弯曲角度小于等于60°的海脊末端远场地区，应进行重点的戒备与防范。当弯曲角度在70°～90°时，继续俘获的能量约在55%以下，而最大的反射能量可以高达约10%左右，此外约42%以上的能量泄漏出海脊。因此在现实海啸中，我们对于海脊的弯曲角度在70°～90°时，由这类海脊连接的远场与近场地区都需要重点防范。

图 5 不同弯曲角度的海脊上俘获波能量变化Fig. 5 Energy of trapped waves over ocean ridges with different curved degree

4 结论

本文采用了MIKE 21-BW 模型，模拟了海啸在不同弯曲角度的海脊上传播变形的过程。结果表明海啸波只有少部分能量以速度较快的自由先驱波在整个海域内传播，大部分被海脊俘获以俘获波的形式沿海脊传播。海啸波被俘获后沿着海脊方向为行进波，俘获波剖面的模拟结果与解析解的0 模态理论吻合良好。海脊俘获波传至海脊转弯处时，少部分能量会泄露出海脊以自由波的形式散射至整个海域，泄露的能量会随着海脊弯曲角度的增加而增加；部分能量会被反射回来形成与初始海啸波相反方向的俘获波继续沿海脊传播，反射的能量会随着海脊弯曲角度的增加而增加；此外还有一部分能量继续沿着弯曲的海脊向前传播，这部分能量随着海脊弯曲的角度增加而减小。