南海北部台风和中尺度暖涡对近惯性振荡的影响
于璐莎,翟荣伟,鲁远征,郭双喜,屈玲,岑显荣,张康,
黄鹏起1,2,尚晓东1,3,周生启1,3*
( 1. 中国科学院南海海洋研究所 热带海洋环境国家重点实验室,广东 广州 510301;2. 中国科学院大学,北京 100049;3. 中国科学院南海生态环境工程创新研究院,广东 广州 510301)
1 引言
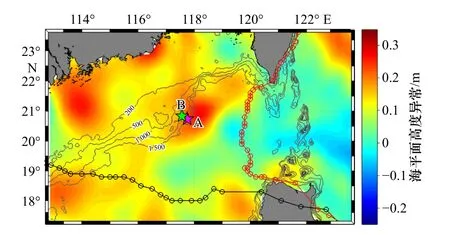
图 1 南海北部2014 年9 月19 日海平面高度异常的分布Fig. 1 Sea level anomaly in the northern of South China Sea on September 19th, 2014
2 数据和方法
2.1 数据
2.1.1 潜标数据
本文采用的数据来源于中国科学院南海海洋研究所的开放航次,该航次于2014 年8 月1 日至9 月27 日在南海东北部东沙群岛附近放置了2 套锚定潜标A 和B。站位A 位于20.736°N,117.745°E,水深1 249 m 处;站位B 位于20.835°N,117.56°E,水深848 m 处(图1),两个站位相距约22 km。站位A 的潜标上放置了3 个ADCP:在440 m 处布放了向上观测的WHS75 kHz ADCP,在450 m 布放了向下观测的WHLS75 kHz ADCP。这两个ADCP 的垂向分辨率为16 m,时间分辨率为2 min。在950 m 布放了向下观测的WHS150 kHz ADCP,垂向分辨率为8 m,时间分辨率为1.5 min。站位B 的潜标上放置了2 个ADCP:在500 m 布放了向上观测的WHLS75 kHz ADCP,以及在520 m 布放了向下观测的WHLS75 kHz ADCP。这两个ADCP 的垂向分辨率为16 m,时间分辨率为2 min。观测期间,有两个台风进入南海,分别为“海鸥”和“凤凰”。台风“海鸥”生成于西北太平洋,9 月14 日在吕宋岛登陆,继而以约30 km/h 的速度向西北方移动(图1),于9 月15 日早上进入南海,早上6 时,距离站位A 最近,下午14 时,距离站位B 最近,距离分别为278 km 和292 km。台风“海鸥”于9 月16 日上午离开南海。台风“凤凰”生成于西太平洋,9 月18 日在吕宋岛登陆,之后以约25 km/h 的速度向西北偏正北方移动(图1),于9 月19 日0 时前后进入南海,9 月20 日0 时,距离站位A 和B 最近,距离分别为209 km 和230 km。台风“凤凰”于9 月21 日0 时前后离开南海。2014 年9 月27 日回收潜标时分别在站位A 和B 处进行了CTD 的测量,获得了温度、盐度和深度等数据。
2.1.2 卫星高度计数据和欧洲天气数据
本文基于2014 年8-9 月的海平面高度异常(Sea Level Anomaly, SLA)和地转流流速数据分析中尺度涡旋的基本特征。数据来源于AVISO (http://www.aviso.oceanobs.com),融合了多种卫星观测数据,数据分辨率为(1/4)°×(1/4)°,时间分辨率为1 d。同时也利用欧洲天气预报中心ERA-Interim 的海表上空10 m 处的风速数据,分析台风进入南海时两个站位所处的大气环境。
2.2 研究方法
2.2.1 斜压近惯性流的提取
正压流体是指流体内部任何一点的压力只与密度有关,而除了与密度有关之外,还与其他热力学参量,如温度、盐度等有关的流体是斜压流体。为了研究海洋内部的动力过程,对于一个长时间观测的海流U(z,t),可将其分解为正压流和斜压流实测海流的深度平均即是正压流,
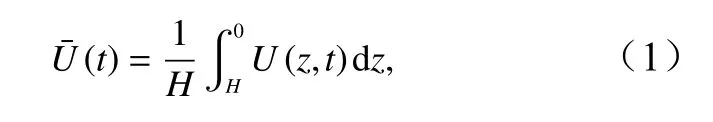
式中,z为深度;t为时间;H为海水总深度。实测海流减去正压流即可得到斜压流
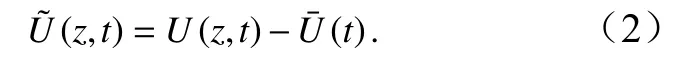
对斜压流进行带通滤波处理,采用Butterworth 滤波器,滤波函数为Matlab 自带的filtfilt 滤波程序,滤波频带为(0.85~1.15)f0,获得近惯性流的变化。其近惯性动能(Near-Inertial Kinetic Energy, NIKE)表示为
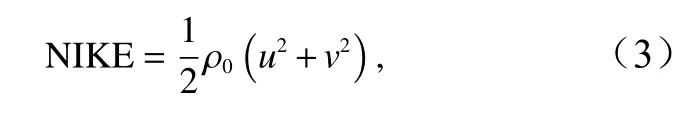
式中,u、v分别为滤波得到的近惯性流的东西和南北向流速分量;ρ0为海水的参考密度,取1 024 kg/m3。
2.2.2 能谱分析
基于Gonella[14]阐述的谱分析方法的数学基础可知,任一水平流速矢量可表达为对其进行傅里叶变换,得到其顺时针分量为
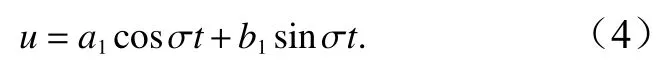
逆时针分量为

流速椭圆可表达为

式中,
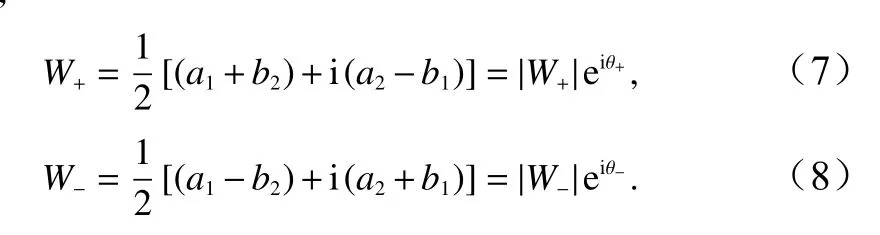
那么,定义顺时针谱为

逆时针谱为

全能谱为

式中,t表示时间,i 为虚数单位,a1、b1、a2、b2为常数,表示振幅,σ表示频率,*表示共轭复数。
2.2.3 涡旋中心的检测
本文参照Halo 等[15-16]的自动检测涡旋的方法,运用两个判据去确定涡旋以及涡旋的中心。一个判据是闭合的海表面高度[17]。另一个是Okubo-Weiss 参数小于0[18-19],其中Okubo-Weiss 参数定义为
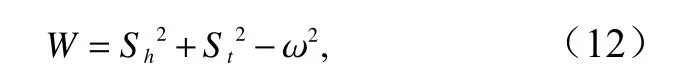
3 结果
3.1 近惯性流场的分析以及对比
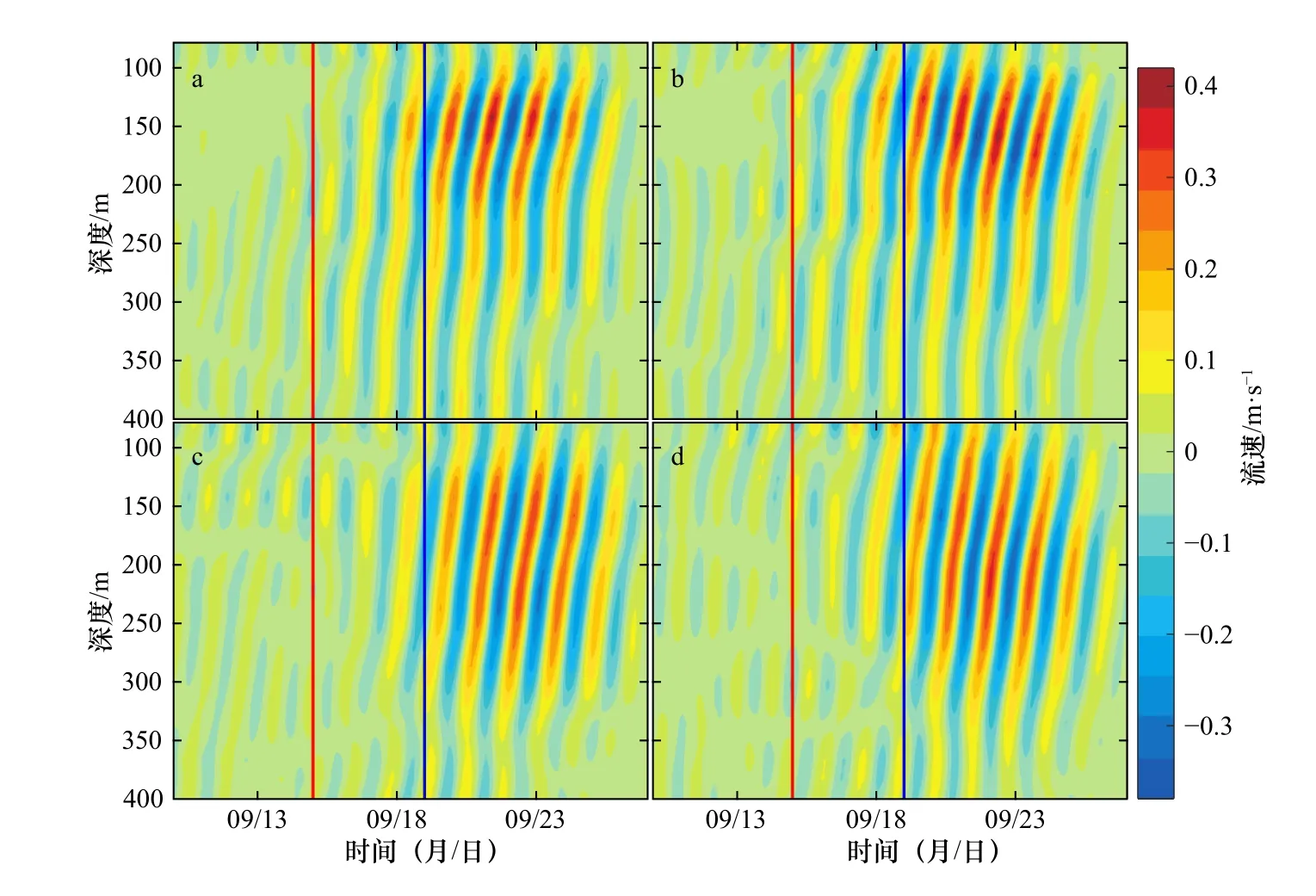
图 2 2014 年9 月10-27 日期间站位A(a,b)和站位B(c,d)近惯性流东西向(a,c)、南北向(b,d)分量随时间和深度的分布Fig. 2 The distribution of the near-inertial current zonal (a, c) and meridional (b, d) velocity at Station A (a, b) and Station B (c, d) from September 10th to 27th, 2014
为了研究两个台风对近惯性流速的影响,滤波后站位A 和B 的近惯性流速如图2 所示。从图2 可以看出,台风“海鸥”过后,两个站位的近惯性流速并没有明显的增强,直至9 月19 日台风“凤凰”进入南海,两个站位的近惯性流速才开始明显增强。其中站位A 的近惯性流速在约158 m 深度处达到最大,最大流速值约为0.41 m/s。站位B 的近惯性流速则在约207 m深度处达到最大,最大流速值约为0.36 m/s,深度较站位A 深49 m。站位A 的近惯性流速东西向和南北向都比站位B 的流速大,分别大0.07 m/s 和0.06 m/s 左右。并且,350 m 以深两个站位的近惯性流速均已较小,平均流速约为0.05 m/s,最大不超过0.1 m/s。由于潜标观测的原因,上层50 m 未采集到数据,所以接下来,我们重点对50~400 m 深度范围的近惯性振荡特征进行研究。
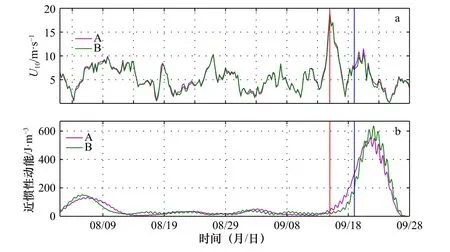
图 3 整个观测期间站位A 和B 上空10 m 处的风速大小(a)和两个站位深度(50 m≤d≤350 m)积分后的近惯性动能(b)随时间变化的分布Fig. 3 Time evolution of the 10 m wind speed (a) and the integrated near-inertial kinetic energy between 50 m and 350 m (b) at Station A and Station B during the entire observational period
3.2 台风激发的近惯性动能的分布特征以及对比
观测期间,站位A 和B 上空10 m 处的风速变化如图3a 所示,可知,9 月15 日上午,台风“海鸥”过境时,风速显著增大,由台风之前的小于10 m/s 变化至19 m/s 和18.5 m/s。而台风“凤凰”过境时,风速并没有明显增大。为了研究台风激发的近惯性振荡的基本特征,对近惯性动能进行深度(50 m≤d≤350 m)积分,得到其总的近惯性动能随时间的变化(图3b)。由图3b 可知,台风“海鸥”过境后,两个站位的近惯性动能虽有所增加但不明显,台风“凤凰”过境之前近惯性动能一直在增加,台风“凤凰”过境时,风速虽没有明显增大,但两个站位的近惯性动能仍在一直增加,直到站位A 于9 月21 日下午13 时达到峰值553.4 J/m3,站位B 滞后约14 个小时达到峰值636.2 J/m3,较站位A 大15%。两个站位的近惯性动能变化明显存在时间上的延迟。这可能与两个站位相距台风的距离不同有关,站位B 距离台风较远。
由于“凤凰”过境时,站位A 和B 处于中尺度暖涡中,风速虽没有明显增大,但近惯性动能却一直持续增加至峰值。我们推测,近惯性动能的峰值可能是两个台风共同作用的结果,也可能是受到中尺度涡的影响。Zhao 等[20]利用平板混合层模型提出,各项同性风应力作用下产生的近惯性振荡,由于应力的存在,能量会从中尺度涡向近惯性振荡传递。并且指出黑潮延伸区是发生这种现象的一个显著的海域,且由于受涡度的影响,暖涡的能量传递效率是冷涡的2 倍。但是,由于近惯性振荡存在一定的延迟,而两个台风过境时间相距很近,潜标观测数据也有限,无法将两个台风单独的作用以及中尺度涡的作用分离出来,现阶段无法给出更为合理的解释,仍需要进一步探讨。
图4a 和4b 分别为两个台风期间,即9 月15-27日期间,站位A 和B 近惯性动能随时间和深度的分布。可知,两个站位的近惯性动能分布特征存在明显的差异,尤其是在垂向方向上。将15-27 日的近惯性动能进行时间积分,得到其在垂向上的分布,如图4c。由图4c 可知,在台风的激发下,两个站位的近惯性动能都快速增加,站位A 的近惯性动能在158 m 处达到最大,最大值为3.01×105J/m3。随着深度的增加,对应深度处的近惯性动能逐渐减小。站位B 的近惯性动能在同样深度158 m 也达到最大,最大值为2.14×105J/m3,比站位A 的小29%。随着深度的增加,对应深度处的近惯性动能缓慢减小,至191 m 的深度,能量相对于最大值仅减小1.66×104J/m3,约为同样深度处站位A 能量减小的15%。站位B 在191 m 以深,近惯性动能反而略有增大,至223 m 处达到第二个峰值,能量增加至2.07×105J/m3。223 m 以深,随着深度的增加,能量才开始迅速的减小。整体而言,站位B 在158~223 m 的深度范围内,近惯性动能的分布存在两个峰值,能量衰减较少。站位A 的能量则随着深度的增加而逐渐减小。关于两个站位的近惯性动能在垂向上分布的差异,接下来我们将从中尺度暖涡以及两个站位所处的层结状态这两方面进行研究。
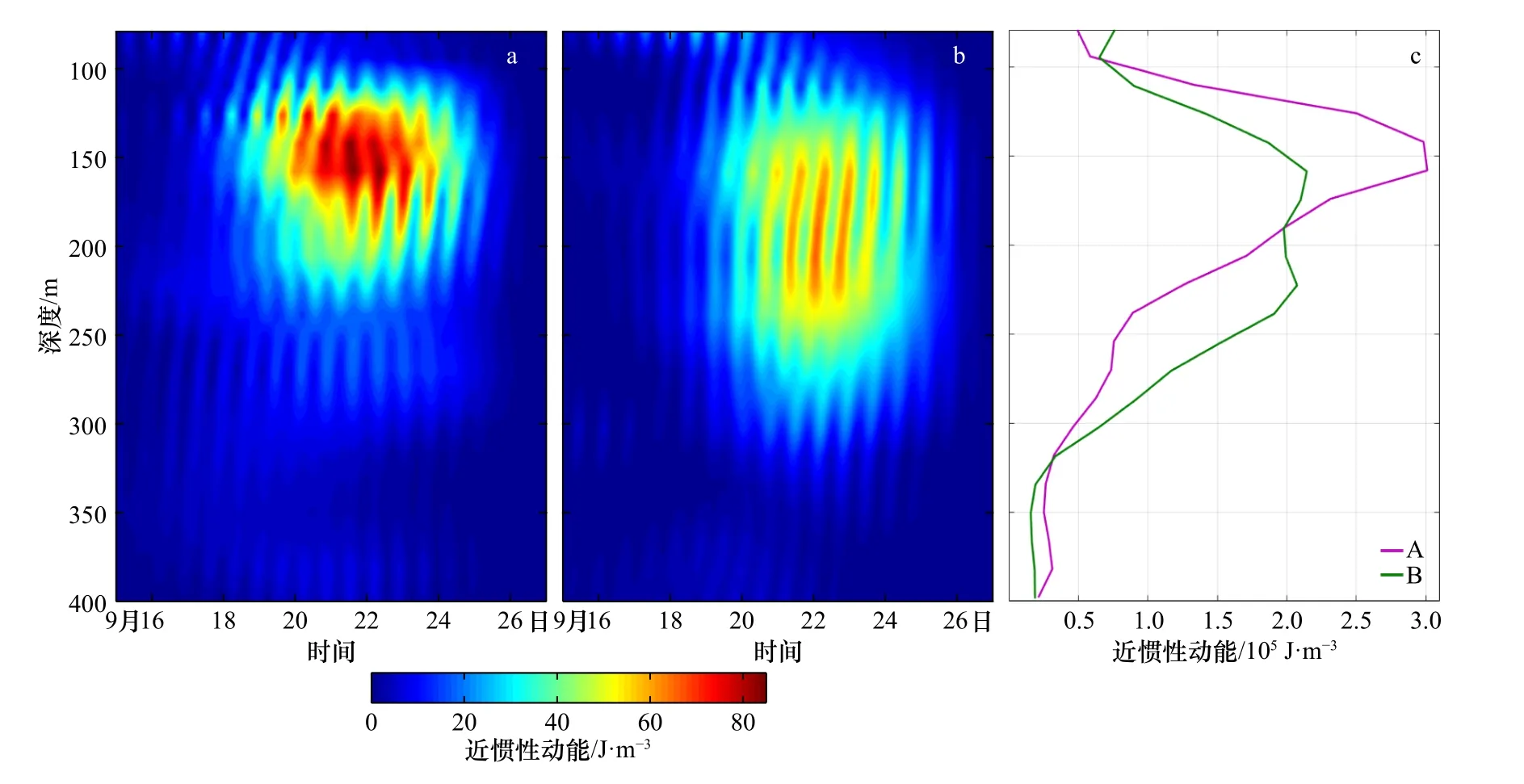
图 4 2014 年9 月15-27 日期间站位A(a)和站位B(b)近惯性动能随时间的分布和两站位15-27 日时间积分后的近惯性动能在垂向上的分布(c)Fig. 4 The time evolutions of near-inertial kinetic energy from September 15th to 27th, 2014 at Station A (a) and StationB (b), and the vertical profiles of time integrated near-inertial kinetic energy of them during this period (c)
3.3 中尺度暖涡
3.3.1 暖涡的基本特征分析以及对流场的影响
基于Halo 等[15-16]自动检测涡旋的方法,在观测期间我们检测出有1 个中尺度暖涡于9 月11 日形成,直至观测结束,该暖涡都一直存在。9 月15 日早上台风“海鸥”到达南海时,站位A 和B 已经受到暖涡的影响(图5 的涡度变化也能显示出)。由图1 可知,9 月19 日台风“凤凰”到达南海时,站位A 和B 处在暖涡的内部。暖涡的平均半径为67 km。图5a 展示了暖涡中心9 月11-30 日期间的移动轨迹以及速度,可知,9 月21-22 日,暖涡的中心移动至两个站位附近,且距离站位A 更近。如图5a 所示,暖涡中心最初向西北方向移动,9 月21 日转向西南方向移动。暖涡中心的平均移动速度为0.12 m/s。涡度为其中ug和vg分别为地转流的东向和北向分量,计算出的平均涡度为-9.45×10-6s-1。
为研究中尺度暖涡对两个站位流速的影响,对流速进行72 h 的低通滤波,得到其低频流速随时间的分布,如图6 所示。站位A 和B 的东西向流速较小,最大值分别为0.12 m/s 和0.19 m/s;两个站位南北向流速较大,并且站位A 北向流速明显较站位B 小,北向最大流速分别为0.16 m/s 和0.36 m/s;而站位A 南向流速明显较站位B 大,南向流速绝对值最大分别为0.22 m/s 和0.18 m/s。由图6b 和6d 可知,由于暖涡的移动,造成两个站位在9 月22 日前后流速方向由北向转为南向。并且,两个站位南北向流速的垂向分布特征表现出明显的不同。在9 月19-21 日台风“凤凰”期间,站位A 受北向流场的影响深度最大只有约200 m,且随着时间推移,越来越浅,减小至100 m 上下;而站位B 受北向流场的影响深度最大可达250 m,且随着时间推移,深度减小较少,维持在约200 m 的深度。由站位A 和B 垂向上的流速分布可知,在近惯性振荡影响的深度范围内,中尺度暖涡引起的站位A 水体的剪切程度较站位B 大。这与上述两个站位近惯性动能的垂向分布特征相一致,即站位B 在158~223 m 的深度范围内,能量相对集中,而站位A 的能量则随着深度增加而减少。关于中尺度暖涡对近惯性动能分布的影响,本文接下来会给出详细的解释。
3.3.2 暖涡涡度对近惯性频率的调制
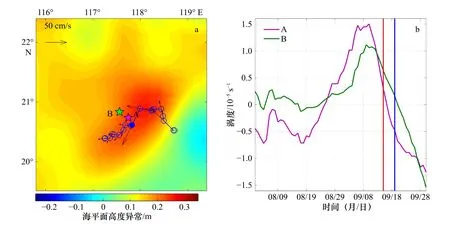
图 5 2014 年9 月21 日海平面高度异常的分布(a)及观测期间站位A 和B 的涡度分布(b)Fig. 5 The distribution of sea level anomaly on September 21st, 2014 (a), and variation of vortices at A and B stations during the observation period (b)
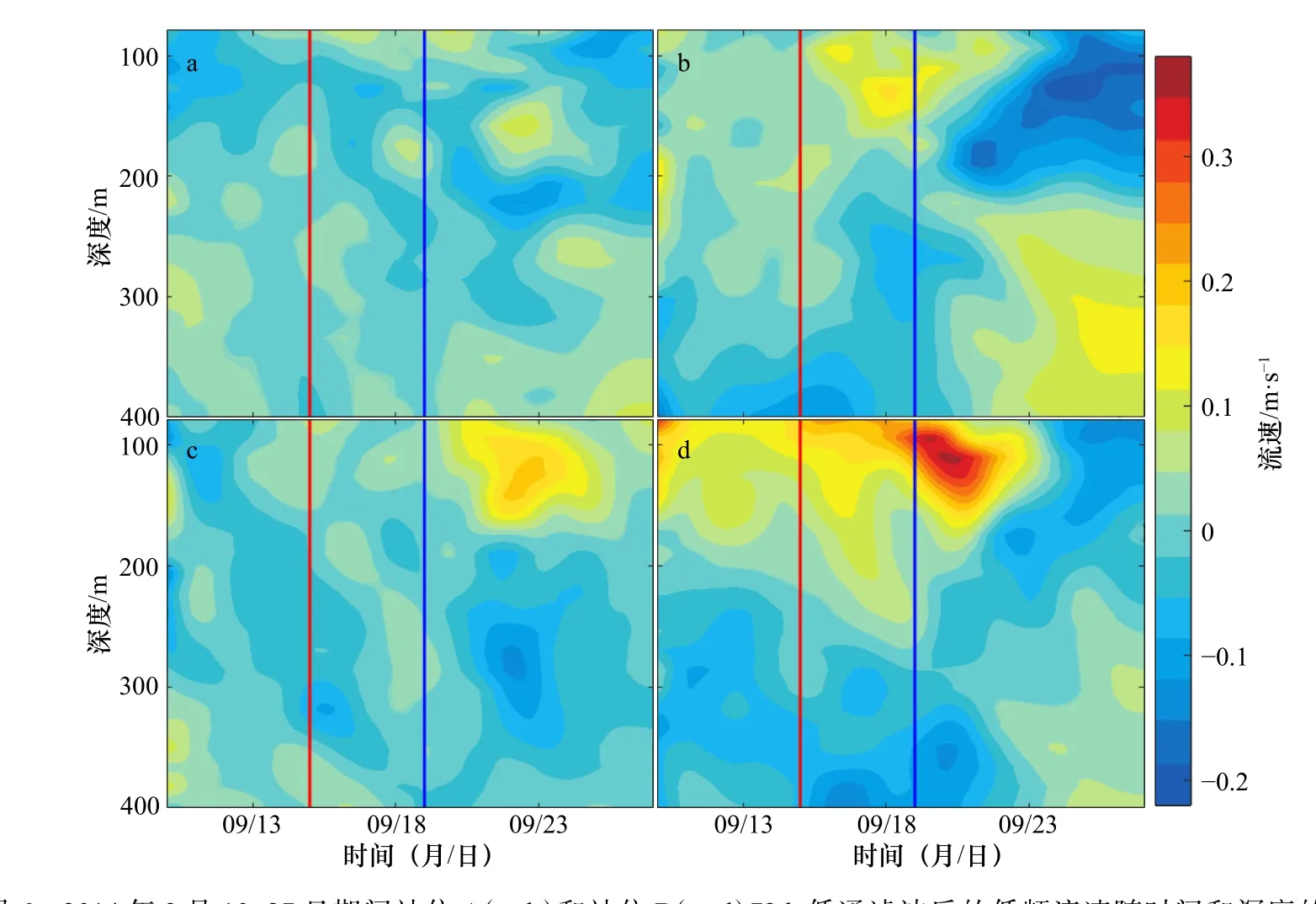
图 6 2014 年9 月10-27 日期间站位A(a,b)和站位B(c,d)72 h 低通滤波后的低频流速随时间和深度的分布Fig. 6 The distribution of low-frequency flow (filtered by 72 h low-pass filter) over time and depth at Station A and Station B during Sptember 15th to 27th, 2014
前人的研究指出,台风激发的近惯性振荡的频率并不会严格等于局地的惯性频率f0,而是会受到背景涡度的调制作用,从而导致近惯性频率增加(蓝移)或减小(红移)[4,6,13]。Chavanne 等[21]指出近惯性振荡的频率取决于参照系的选取,不同的参照系下,比如旋转参照系、非旋转参照系以及与地球一起旋转的参照系等,对应的频率不同。而Whitt 和Thomas[22]利用平板混合层模型和二维数值模拟,研究出地转流的垂直涡度会修正有效科里奥利频率。Kunze[6]指出近惯性振荡激发的有效频率fe与局地的惯性频率f0之间存在关系:其中,ζ为背景涡度。若近惯性振荡发生在中尺度暖涡(冷涡)内部,背景水体的负(正)的涡度会使得近惯性振荡的有效频率fe小于(大于)局地的惯性频率f0,即造成近惯性频率的红移(蓝移)。9 月15 日台风“海鸥”进入南海时,暖涡已经形成,其边缘靠近站位A 和B,由图1 展示的海平面高度异常分布可知,9 月19 日台风“凤凰”进入南海时,两个站位已经在暖涡的内部,并且直至观测结束,该暖涡均一直存在(图5a)。为了研究台风对近惯性振荡的影响,以及暖涡对近惯性频率的调制作用,两个站位在台风(暖涡)之前(2014 年8 月26 日至9 月11 日)和之后(2014 年9 月15-27 日)的动能谱随深度的分布如图7 所示。图7b 和7d 表明,台风显著增加了近惯性频率的能量,且站位A 的较站位B 的大。站位A 在78~142 m 深度范围内,近惯性频率小于局地惯性频率f0,即发生了近惯性频率的红移(图7b)。由0.710 1 周/d 红移至0.659 2 周/d,减小了7.2%;站位B 在79~175 m 的深度范围内,近惯性频率也发生红移(图7d)。由0.713 3 周/d 红移至0.659 2 周/d,减小了7.6%。由此可知,中尺度暖涡对站位B 近惯性频率的调制作用较站位A 的大,并且站位B 红移的深度较站位A 深32 m。两个站位的背景水体的涡度随时间的分布如图5b 所示。9 月15 日台风“海鸥”和9 月19 日“凤凰”进入南海后,两个站位的背景水体的涡度逐渐由正转负,并且负的涡度的绝对值越来越大。9 月15-27 日期间,两站位背景水体的涡度的平均值分别为-6.57×10-6s-1和-2.05×10-6s-1,参照Kunze[6]提出的关系式,对有效近惯性振荡频率fe的平均贡献分别为-0.045 2 周/d 和0.014 1 周/d。截至9 月27 日,两个站位负涡度达到的绝对值的最大值分别为9.94×10-6s-1和1.03×10-5s-1,对近惯性频率的调制与实际观测的结果相吻合。

图 7 站位A(a,b)和B(c,d)台风之前(a,c)和之后(b,d)的动能谱断面分布Fig. 7 Power spectra before (a,c) and after (b,d) typhoon of Station A (a,b) and Station B(c,d)
3.3.3 暖涡对近惯性动能的分布和传播的影响
台风向海洋的混合层输入近惯性能量,这部分能量会通过水平辐散、垂向传播和局地耗散等途径最终衰减掉[1-2]。近惯性动能由最大值减少到最大值的1/e 所用的时间定义为e 折时间尺度。由此我们估算,站位A 和B 的e 折时间尺度分别为4.3 d 和3.9 d,相差约9 h。
站位A 和B 相距仅22 km,近惯性动能在垂向上的分布特征却明显不同(图4)。由图6 可知,中尺度暖涡会造成水体垂向上的强水平剪切,改变水体的层结状态。近惯性动能在向下传播的过程中,不同的层结对能量的传播具有不同程度的折射作用,即水体的层结状态会影响近惯性动能的分布和传播。为了评估层结对能量分布和传播的影响,参照1975 年Leaman 和Sanford[23]提出的方法,我们对近惯性流速和近惯性动能进行了“Wentzel-Kramers-Brillouin (WKB)”近似。其中,近惯性流速的WKB 近似公式如下式所示,

近惯性动能的WKB 近似公式如下式所示,
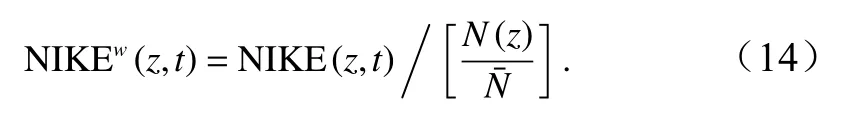
图8a 显示了WKB 因子随深度的变化,可知,A 和B 两站位WKB 近似之后的近惯性动能,与原始的近惯性动能相比,在不同层结中相差约0.5~3 倍。管守德[1]利用南海北部潜标数据分析层结对能量分布的影响时,发现在WKB 近似后,近惯性动能在不同层结中相差0.5~2.5 倍。与原始近惯性动能相比,站位A 在WKB 近似之后的近惯性动能在158 m 达到峰值,之后随着深度的增加,近惯性动能依然迅速减小。而站位B 在WKB 近似之后的近惯性动能在158 m达到峰值之后先减小,在200 m 附近又开始增加,在238 m 深度处,由于较弱的层结,较小的WKB 因子,近惯性动能增加至原来的3 倍,达到第二个峰值,并且能量比第一个峰值对应的能量大。可见,如若排除层结的影响,站位B 的近惯性动能在垂向上的分布具有双峰结构。上层的能量峰值来源于台风的激发作用,下层的峰值则原因不明,我们推测可能是有能量的外源输入,具体原因仍需进一步探讨。从另一个角度说,也正是因为中尺度暖涡改变水体的层结状态,而水体层结对能量的折射作用,才使得站位B 的近惯性动能在158~223 m 之间减小较少,得以往更深处传播,而站位A 的近惯性动能则随着深度增加迅速减小。
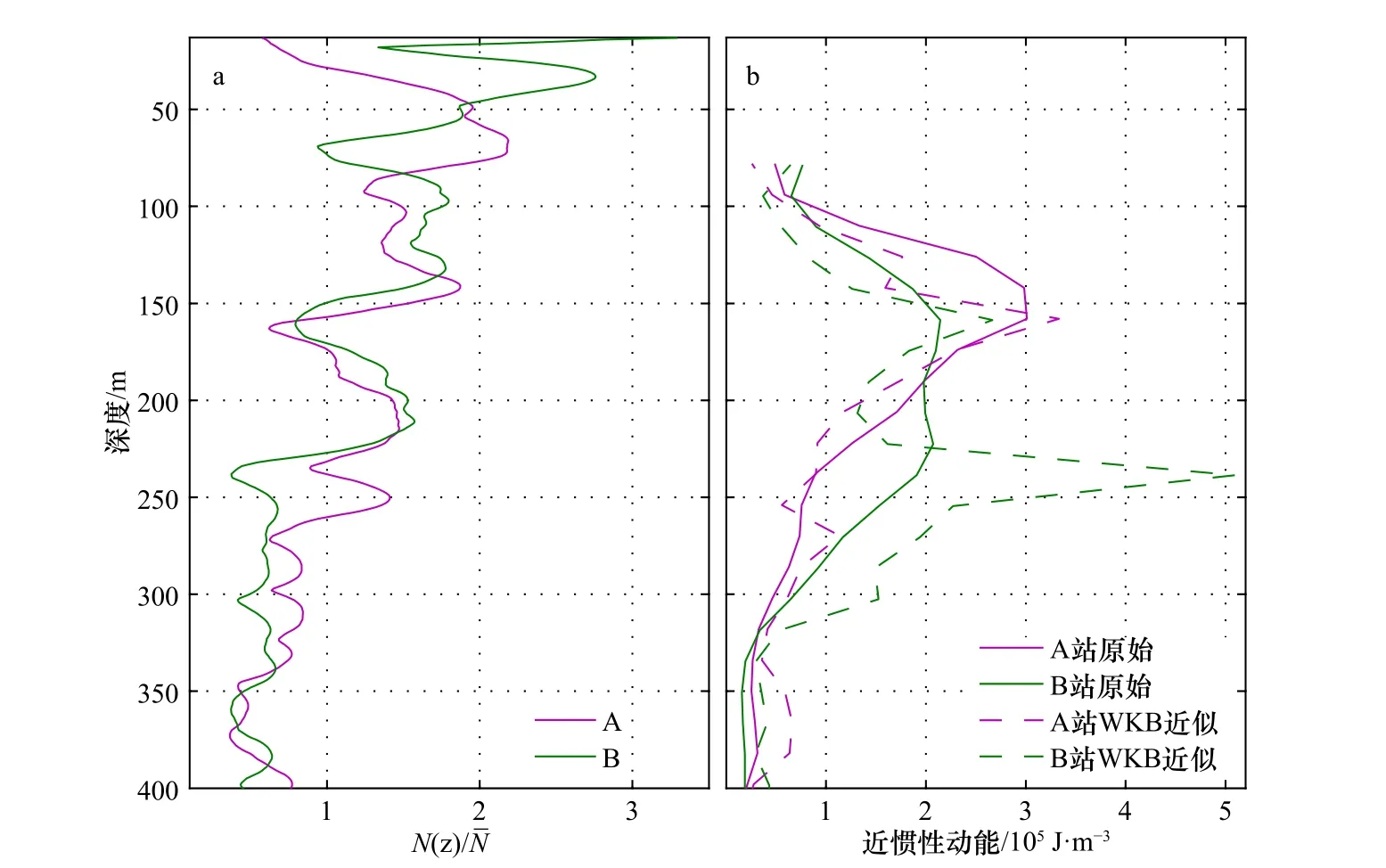
图8 WKB 因子垂向上两个站位原始的近惯性动能(实线)和WKB近似后的近惯性动能(虚线)(b)Fig. 8 The WKB scaling facto raw near-inertial kinetic energy(solid lines) andWKB-scaled near-inertial kinetic energy (dash lines) of Station A and Station B (b)
另外,由图2 可知,台风激发的近惯性流速的分布明显向右上方倾斜,说明近惯性流速的相位具有明显的上传趋势。在连续介质中传播的内波的一个重要特征就是群速度与相速度垂直[3]。相位上传,则说明其垂向群速度是向下的,能量以近惯性内波波群的形式向海洋深层传播。为了估算近惯性动能在垂向上的传播,根据Qi 等[24]提出的方法,在WKB 因子近似下,如图9 所示,我们估算了两个站位近惯性内波的垂向群速度Cg(z),站位A 大于站位B,分别约为15.2 m/d 和14.1 m/d。如果只考虑近惯性动能在垂向上的传播,即不考虑其在水平方向上的辐散,参照管守德[1]的计算方法,两个站位350 m 以浅近惯性动能衰减的理论e 折时间尺度分别为9.2 d 和9.9 d,远大于实际e 折时间尺度(4.3 d 和3.8 d),因此,在总近惯性动能衰减至其1/e 时的时间范围内,忽略能量水平辐散的情况下,近惯性内波的垂向传播使得站位A 的近惯性动能衰减了约47%,站位B 的近惯性动能衰减了约38%,较站位A 的少。管守德[1]也得出类似结论,指出近惯性内部的垂向传播使得近惯性动能只衰减了约33%。其余近惯性动能将通过内波破碎或是非线性的波波相互作用在局地耗散掉。
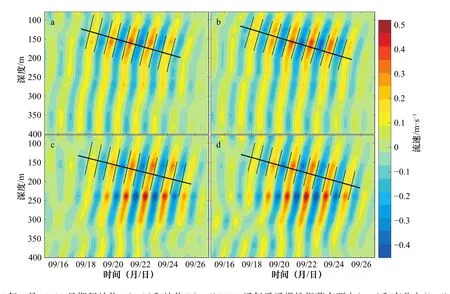
图 9 2014 年9 月15-27 日期间站位A(a,b)和站位B(c,d)WKB 近似后近惯性振荡东西向(a,c)和南北向(b,d)流速随时间和深度的分布Fig. 9 The distribution of the WKB-scaled near-inertial current (a, c) and meridional (b, d) velocity at Station A (a, b) and Station B (c, d)from September 10th to 27th, 2014
4 结论
本文基于2014 年8-9 月在南海北部东沙群岛附近海域观测的两个不同水深站位A 和B 的潜标数据,对比研究了两个站位在台风“海鸥”和“凤凰”的激发下产生的近惯性振荡的特征,并重点分析了中尺度暖涡对近惯性振荡频率的调制作用,以及对近惯性动能的传播和分布的影响,结果如下:
(1)9 月15 日台风“海鸥”进入南海,站位A 和B 的近惯性流速没有明显变化,直至9 月19 日台风“凤凰”进入南海后,两个站位的近惯性流速明显增大。站位A 的近惯性流速最大可达0.41 m/s,站位B 最大可达0.36 m/s。两个站位的近惯性动能在垂向上的分布特征表现出明显的差异。时间积分下的近惯性动能从表层随着深度增加,站位A 在158 m 处达到最大,最大值为3.01×105J/m3。站位B 在158 m 也达到最大,最大值为2.14×105J/m3,随着深度增加,在158~223 m 的深度范围内,近惯性动能的分布存在两个峰值,能量减小较少。我们推测,这与层结对能量的折射作用有关。中尺度暖涡引起水体垂向上的强水平剪切,从而改变水体的层结状态。两个站位的近惯性动能在不同层结中被缩小或放大了约0.5~3倍。若排除层结的影响,站位B 的近惯性动能则具有双峰结构。具体原因仍需进一步探讨。
(2)中尺度暖涡的平均半径为67 km,平均涡度为-9.45×10-6s-1,且站位A 更靠近暖涡中心。暖涡中心移动的平均速度为0.12 m/s。两个站位72 h 低通滤波后的低频流速南北向较大,且中尺度暖涡引起的站位A 水体的剪切程度较站位B 强。暖涡的涡度对近惯性频率具有调制作用,站位A 在78~142 m 的深度范围内,近惯性频率出现了红移。由0.710 1 周/d 红移至0.659 2 周/d,减小了7.2%;站位B 在79~175 m的深度范围内,近惯性频率出现了红移。由0.713 3 周/d红移至0.659 2 周/d,减小了7.6%。暖涡对近惯性频率的调制作用与两个站位所处的背景涡度值相吻合。
(3)台风激发的近惯性流速的相位具有明显的上传趋势,垂向群速度是向下的,近惯性动能以近惯性内波波群的形式向海洋深层传播。两个站位近惯性内波的垂向群速度Cg(z)分别约为15.2 m/d 和14.1 m/d,近惯性动能衰减的理论e 折时间尺度分别为9.2 d 和9.9 d,远大于实际e 折时间尺度(4.3 d 和3.8 d),因此,在总近惯性动能衰减至其1/e 时的时间范围内,忽略能量水平辐散的情况下,近惯性内波的垂向传播造成了站位A 约47%的近惯性动能衰减,站位B 约38%的近惯性动能衰减。

