适于模拟不规则水域波浪的缓坡方程两种数值模型比较

李巧生，唐军，吕义港

( 1. 苏州市航道管理处，江苏 苏州 215008；2. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116023；3. 嘉兴市交通工程质量安全管理服务中心，浙江 嘉兴 314001)

1 引言

波浪是近岸环境中最重要的水动力因素之一，影响到水工建筑物的规划和设计，也是近岸泥沙运动、岸线演变的主要动力。波浪从外海向近岸传播过程中，受到地形、岸界等影响，发生折射、绕射、反射等变形。近岸波浪数值模拟是分析波浪传播变形特性的主要手段，也是海岸工程水动力分析的理论技术基础。缓坡方程波浪模型[1]综合考虑了波浪传播过程中的反射、折射和绕射等效应，可有效地模拟近岸缓坡区域波浪的传播变形，被广泛应用于近岸波浪场的模拟分析[2-6]。

近岸波浪数值模拟时，通过在规则矩形网格下对波浪模型离散求解。在天然近岸水域，受海岸建筑物（码头、防波堤等）、岛屿、不规则岸线等影响，波浪运动的水域通常比较复杂、不规则，采用矩形网格拟合必然会造成计算域边界与实际边界吻合较差，影响到数值模拟精度。为适应工程实际中常有的不规则曲折边界，研究者们在数值模型中引入了曲线网格和非结构化网格，但其求解的方程组不是对角占优，网格偏离正交时会产生复杂的交叉项，所需内存较大，计算时间长。因此，引入一种对复杂计算边界适应性好，并且计算过程简单、稳定收敛的数值方法是很有必要的。

近年来，非结构化计算网格和四叉树计算网格因对复杂计算边界适应性好，逐渐被用于水动力数值模拟[3-4,6]。Guo 等[7]基于非结构化网格下的有限体积法，建立了河口潮流数值模型，模拟了钱塘江口的潮流及波浪变化，取得了较好的效果；林伟波和王义刚[8]采用非结构化网格的海洋模型，建立了瓯江口三维潮流数值模型，较好地模拟了瓯江口潮流及波浪的时空分布特征；Zhang 等[9]应用Quadtree 非结构网格，采用有限体积方法离散方程，利用预条件的不完全Lu 分解方法加速其收敛性、提高计算效率；Wu 和Li[10]采用自适应网格技术，考虑动水压强的影响，建立了垂向二维开挖明渠的数值模型；华祖林等[11]基于四叉树网格布设的思想，分层次对不同研究区域按不同尺度网格对近海水域进行嵌套网格联合布置，实现了在不同尺度的网格联立求解，提高了数值计算效率，又保证了计算精度。本文采用有限体积法分别基于自适应四叉树计算网格和非结构化三角形计算网格建立了近岸波浪椭圆型缓坡方程的数值模型，结合典型物理模型实验结构对所建模型分别进行了分析验证，并结合算例分析比较了两种模型的计算精度和效率。计算结果表明，两种数值模型均可有效地模拟近岸波浪的传播变形；相对非结构化三角形网格下的模型，基于自适应四叉树网格建立的数值模型在数值离散和求解过程中无需引入形函数、不产生复杂的交叉项，离散简单，易于程序实现，且节约计算存储空间，计算效率高。

2 数值模型

2.1 椭圆型缓坡方程波浪模型

Berkhoff[1]提出的椭圆型缓坡方程考虑了波浪传播过程中的折射、反射和绕射效应，方程如下：

对于外海入射的简谐波，如果入射波速度势已知，则波浪边界条件可由如下关系式给出：

（1）外海入射边界

（2）下游和侧边界条件

图 1 四叉树网格不同分级单元间的通量计算Fig. 1 Flux across different graded cell interfaces

2.2 基于四叉树网格的数值模型

2.2.1 四叉树计算网格

四叉树网格的生成方法可概括为以下3 个步骤[12-13]：

（1）初始化网格，剖分计算域。初步创建一组很粗但满足要求的四叉树网格。

（2）网格自适应加密。根据网格单元属性，遍历整个四叉树，依据计算精度不断地递归细分，生成新的四叉树网格，直到所有四叉树网格的尺寸满足必要的精度要求。本文中，以地形水深及波长为剖分标准。

（3）输出结果。遍历整个四叉树并输出网格属性、单元编号、计算节点坐标等。

自适应四叉树网格的生成可能使得相邻单元间的级别不一（为确保过渡处变量的连续性，设定相邻网格的级差最多为1），本文采用线性插值来估算不同分级单元间通量。四叉树网格下相邻计算节点的布置可归纳为图1 所示的4 种情形。其中为虚拟单元为当前计算单元，不同级别间单元的通量计算可以通过得到，虚拟单元上守恒物理量的q值按图1 对应的4 种情形计算[7-8]。

2.2.2 四叉树网格下的数值模型离散

（1）同级别四叉树网格下的方程离散

在自适应四叉树网格下结合有限体积法对式（1）在控制容积上积分得：

利用格林函数法，将式（4）中的第一项的面积分转化为线积分并写成求和的形式：

式中，A为控制体的面积为控制体到相邻单元体边的法向矢量；为控制体界面总个数，分别为控制体的西、南、东、北4 个方向上界面数。

I

对于式（4）中的第二项，可用控制单元 中心处的变量来表示对其控制容积积分

由式（5）、式（6）最后可得控制方程（1）的离散形式为

（2）不同级别四叉树网格下的方程离散

以图1a 为例推导式（4）的离散方程

整理得：

2.3 基于非结构化三角形网格的数值模型

2.3.1 非结构化三角形计算网格

本文采用Delaunay 三角形法[14-15]是生成非结构化网格。网格生成可概括为以下5 个步骤：

（1）初始化网格。给定求解计算域边界上的节点信息，将其作为初始的三角形顶点，形成一组很粗的但是满足Delaunay 三角形要求的网格。

（2）不断向区域内部加点并与已有的点组成新的三角形。引入了两个几何参数—长度标尺和外接圆无量纲半径。循环以三角形的外心为新的节点，并利用上面的Delaunay 三角化方法生成新的三角形，直到所有三角形达到形状和尺寸的要求。

（3）网格加密。根据计算的要求，可通过人为加密边界上网格点的方法在局部区域加密网格。

（4）网格光顺化处理。这里采用Laplace 光顺化的方法，即移动每个内部网格点使它成为包围它的多边形的重心。

（5）输出结果。一般包括边界网格点的个数及编号；三角形的个数和编号；三角形三个顶点的编号；所有网格点的坐标。

2.3.2 Delaunay 三角形网格下的方程离散

结合有限体积法，计算节点布置在单元中心，控制容积即为网格单元。对式（1）在的第一项，利用格林函数法将面积分转化为线积分并写成求和形式，

对于式（10）中的第二项，对其控制体积分可用中心处的计算节点的变量来表示，

由式（10）、式（11）最后可得控制方程（1）的离散方程为

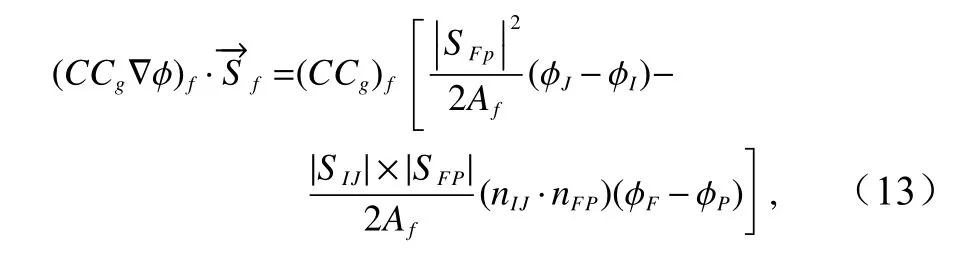
将式（13）代入式（12），就得到以 为计算中心节点的控制体的离散方程，整理后得到一般形式为

图 2 格林函数法计算示意图Fig. 2 Diagram of Green function method

其中，

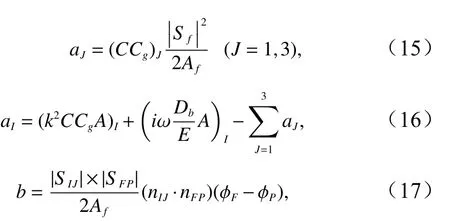
2.4 方程迭代的收敛准则

方程组的离散求解采用GPBiSTAB 法求解[2]。计算时，采用前后两次迭代相对偏差小于某一固定值的方法作为停止方程组内迭代求解的准则[2]，本文中取

3 数值模型验证及结果分析

3.1 圆形浅滩上的波浪传播变形

Ito 和Tanimoto[16]于1972 年进行了圆形浅滩地形上波浪传播变形的模型实验，并给出了3 个断面的波高实测值。实验中入射波高H*=0.010 4 m，周期T=0.511 s，波浪沿x轴正向入射。计算域平面示意图及测量断面的布置见图3。在水深为0.15 m 的平底上布置一圆形浅滩，浅滩中心水深为0.05 m，计算域外水深为恒定值，浅滩上水深[16]为

图 3 圆形浅滩计算域地形示意图Fig. 3 Topography of a circular shoal zone

图 4 圆形浅滩计算域网格图Fig. 4 Numerical grids of a circular shoal zone

计算域取为3.2 m×2.4 m，相邻的计算节点间距控制在0.03 m 左右，从而保证一个波长内至少有8 个计算节点。起始边界采用入射边界条件，其他边界取为辐射边界条件。图4 给出了两种网格模型下整个计算区域网格图。图5 给出了两种网格模型下整个计算区域数值模拟相对波高等值线图，由图可以看出，由于圆形浅滩的存在使得波浪发生折射和绕射，在圆形浅滩后明显存在波高的汇聚区。图6 给出了两种模型在该地形下3 个断面的数值解和实测值[16]的比较，可以看出各断面计算值和实测值均符合的比较良好。表1 是相同计算机下两种模型的计算效率比较，可以看出四叉树计算网格下的网格数量明显要小于三角形网格，且模型的计算时间优于三角形计算网格。

图 5 圆形浅滩数值模拟相对波高等值线图Fig. 5 Contours of simulated wave height for wave propagation on a circular shoal

图 6 圆形浅滩地形上波高数值解与实测值[16]的比较Fig. 6 Comparison between numerical simulated and measured[16] wave heights on a circular shoal

3.2 椭圆形浅滩上的波浪传播变形

Berkhoff 等[17]于1982 年进行了椭圆形浅滩的模型实验，实验中入射波高H*=0.023 2 m，周期T=1.0 s，波浪沿x轴正向入射。实验给出了相对波高等值线图以及8 个断面的实测资料。

计算域平面示意图及测量断面的布置见图7。在均匀的斜坡上布置一椭圆形浅滩，斜坡梯度为1∶50，斜坡梯度方向与波浪入射边界的法向夹角为20°，水

表 1 圆形浅滩地形上两种计算网格下的模型效率比较Table 1 Comparison of the efficiency for the model in two kind of numerical grids on a circular shoal

图 7 椭圆形浅滩计算域地形Fig. 7 Topography of a elliptic shoal zone

深由旋转后的新坐标确定[17]

椭圆形边界定义为[17]

平底区及斜坡上的水深为[17]

而椭圆形浅滩上的水深为[17]

图 8 椭圆形浅滩计算域网格图Fig. 8 Numerical grids of an elliptic shoal zone

计算域取21.5 m×20.0 m，相邻的计算节点间距控制在0.12 m 左右，从而保证一个波长内至少有8 个计算节点。起始边界采用入射边界条件，其他边界取为辐射边界条件。图8 是两种模型的计算网格图，图9和图10 给出了整个计算区域及8 个断面相对波高等值线图。由图9 可以看出由于浅滩的存在使得波浪发生折射和绕射，在椭圆形浅滩后明显存在波高的汇聚区。由图10 可以看出两种模型计算结果和实测值[17]都符合较好，而四叉树网格下椭圆型缓坡方程的数值模型计算结果和实验结果总体吻合更好。表2 是相同计算机下的两种模型效率比较，可以看出四叉树计算网格下的网格数量明显要小于三角形网格，且模型的计算时间优于三角形计算网格。

图 9 椭圆形浅滩数值模拟相对波高等值线图Fig. 9 Contours of simulated wave height for wave propagation on an elliptic shoal

图 10

4 结论

本文分析比较了两种适于不规则水域波浪模拟的椭圆型缓坡方程数值模型。两种模型均采用有限体积法离散，分别基于四叉树网格和非结构化三角形网格建立。首先结合近岸波浪传播的典型物理模型实验对两种数值模型分别进行了验证，并结合计算结果对比分析了两种模型的计算精度和效率。计算结果表明，两种数值模型均可有效地模拟近岸波浪的传播变形；相对非结构化三角形网格下的模型，基于自适应四叉树网格建立的数值模型在数值离散和求解过程中无需引入形函数、不产生复杂的交叉项，离散简单，特别是特别三级以内的自适应四叉树网格易于程序实现，且节约计算存储空间，计算效率高。

图 10 椭圆形浅滩地形上波高数值解与实测值[17]的比较Fig. 10 Comparison between numerical simulated and measured [17] wave heights on an elliptic shoal

表 2 椭圆形浅滩地形上两种计算网格下的模型效率比较Table 2 Comparison of the efficiency for the model in two kind of numerical grids on an elliptic shoal