一种新扩频码的性能分析

马旭辉，荆文芳

（1.中国科学院 国家授时中心，西安710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安710600；3.中国科学院大学，北京100049；4.中国科学院大学 电子电气与通信工程学院，北京101048）

0 引言

卫星导航定位系统大多采用扩频技术来传输导航信息，因此扩频码的优劣对卫星导航信号的性能有决定性影响。一方面，扩频码起到区分导航卫星的作用；另一方面，扩频码用于测距，其性能的优劣直接影响定位精度。此外，扩频码还影响导航信号功率谱的起伏。正因为扩频码如此重要，对扩频码的研究从未停止过，并且扩频码的设计思路正变得越来越宽。传统的卫星导航信号扩频码采用线性反馈移位寄存器产生，如m序列和Gold码，这两种扩频码存在线性复杂度低的缺点，保密性受到一定威胁。文献[1]提出了一种新的混沌序列扩频码，该扩频码不仅具有良好的捕获性能和抗窄带干扰性能，同时保持了Gold码的高跟踪性能，而且显著提高了复杂度，加强了可靠性和安全性。文献[2]提出一种非等长的扩频码设计方法，改善了强多址干扰环境下弱信号的捕获性能。文献[3]提出的正交扩频码构造方法具有很强的普适性，利用该方法生成的扩频码具有优良的相关性和线性复杂度。本文借鉴该方法，构造了一种全新的扩频码，并对新扩频码的性能进行了分析。

本文主要分为3部分，首先分析了新扩频码的构造方法并给出构造流程图，其次在相关性、平衡性、游程性、线性复杂度4个方面与传统扩频码进行了对比分析，最后在Matlab中建立多用户的DS-CDMA模型进行仿真，验证了新扩频码的可行性和优势。

1 新扩频码的构造方法

本节以Kasami序列为切入点展开，首先介绍Kasami序列。

Kasami序列是1966年在评估线性循环码的权重过程中发现的，分为小集合序列和大集合序列，都是在m序列的基础上产生的。由于Kasami小集合序列的相关性性能优于大集合序列，因此实际应用中多用Kasami小集合序列。Kasami小集合序列是选择周期为 21n N=-的m序列，因为总是可以分成两个相邻奇数的乘积，即：，所以对周期为N的m序列每隔抽样，产生长度为的序列，将新产生的序列重复次，得到与m序列长度相等的新序列，将新序列与选择的m序列逐位模二加就可以得到Kasami小集合序列。更进一步，我们可以发现一定可以被3整除。可用数学归纳法证明如下：①当时，N=(21+1)(21+1)=3×1显然成立；②假设时成立，即N=(2k+1)(2k-1)能被3整除；③当时，N=(2k+2+1)(2k+2-1)=[3×2k+(2k+1)][3×2k+(2k-1)]。

由式②可知式③也能被3整除。

因此周期为N的m序列可以进一步分解为：，其中N1为3，N2为。

新Kasami序列与Kasami小集合序列的生成方法相同，不同的是抽样频率，Kasami小集合序列对周期N进行了一次因式分解，分解成两个相连奇数的乘积，新Kasami序列是对其中的一个因子继续进行分解，分解成3和另外一个因数。新Kasami序列以频率N1对周期为N的m序列抽样得到序列B，将B进行N2次循环移位得到与m序列等长的序列B′，之后与选择的m序列逐位模二加得到新Kasami序列。新Kasami序列的构造流程如图1所示。

图1 新Kasami序列的构造流程

H.Donelan和T.O.Farrell在1999年提出了一种新的扩频码构造方法，该方法使用两组m序列，通过矩阵运算生成正交序列集，生成的正交扩频码具有良好的相关性和线性复杂度。本文参考该方法，选择两个相互正交的新Kasami序列，以新Kasami序列为基础构造矩阵，通过矩阵运算得到矩阵M，矩阵M的每一行即是一个新扩频码。新扩频码的构造流程如图2所示。

图2 新扩频码构造流程

2 性能对比分析

扩频码的优劣对卫星导航信号的性能有决定性影响[4]，本节对扩频码的性能分析包括相关性、平衡性、游程性以及线性复杂度。

2.1 相关性

在扩频码的实际应用中，首先要考虑的关键因素是自相关性和互相关性。对于周期为N的二值扩频码序列X{x1，x2，…，xN}、Y{y1，y2，…，yN}，其自相关函数和互相关函数的定义可描述为：

式（1）和（2）中，PAC(l)与PCC(l)分别代表自相关和互相关，l代表码片移位值，Xk代表第k个码片。

可以通过相关旁瓣能量，定量分析扩频码的性能，相关旁瓣能量越大，说明相关函数旁瓣峰值越大，扩频码性能就越差，反之扩频码性能就越好。最大相关旁瓣能量表示为

首先，定性分析新扩频码的相关性。在Matlab仿真平台下，取新扩频码的级数为4、6、8、10，分别仿真分析新扩频码的归一化自相关性和归一化互相关性，如图3至图6所示。

图3 新扩频码级数为4的仿真分析的相关性

图4 新扩频码级数为6的仿真分析的相关性

图5 新扩频码级数为8的仿真分析的相关性

图6 新扩频码级数为10的仿真分析的相关性

从图3至图6可以看出，随着序列长度的增加，新扩频码的自相关函数的主瓣表现为δ函数，主瓣与旁瓣峰值比越大，自相关性越好。良好的自相关性能有利于提高系统的抗干扰能力，便于信号的接收和检测，提高信号的捕获速度和跟踪精度，这样的特性满足高精度测距的要求。互相关函数随着序列长度的增加，越来越趋近于0，良好的互相关性可以提高频谱利用率，降低各系统信号之间互相干扰的影响[5]。

为了定量分析新扩频码的相关性，本文对比了新扩频码、Gold码以及Kasami小集合序列的最大自相关旁瓣能量和互相关峰值能量，如表1和表2所示。

表1 3种扩频码的最大自相关旁瓣 dB

由表1可以看出，最大自相关旁瓣的功率随着序列长度的增加而逐渐降低，新扩频码的自相关性能与Gold基本相当，比Kasami小集合序列稍逊一筹。总的来说，新扩频码能够满足卫星导航定位系统对信号的捕获和跟踪需求[6]。

表2 3种扩频码的互相关峰值 dB

由表2可以看出，3种扩频码的互相关峰值功率随着序列长度的增加而降低，新扩频码的互相关性能要优于Kasami小集合序列，与Gold码基本相当。总之，新扩频码的互相关性能优异，可以降低多址干扰，提高卫星导航定位系统的信号传输质量以及系统容量[7]。

2.2 平衡性

扩频码的平衡性与系统的载波抑制度有关，如果扩频码不平衡，则会造成卫星导航定位系统载波泄漏，降低系统的保密性、抗干扰和抗侦破能力[8]。

平衡度E定义为:

式（4）中，L表示序列的长度，P表示序列中1的个数，Q表示序列中0的个数。E越小，序列的平衡度越好，性能越好。

在Matlab仿真平台下，根据上述平衡度的定义，取序列的级数分别为4、6、8、10，将新扩频码、Gold码以及Kasami小集合序列3种扩频码，做平衡度的对比仿真分析，如图7所示。

从图7可以看出，随着序列级数的增加，3种扩频码的平衡度都在降低，越来越接近0。新扩频码的平衡性介于Gold码和Kasami小集合序列之间。总体表明，该扩频码能够抑制卫星导航定位系统的载波泄漏，提高导航定位系统的保密性和抗干扰能力[9]。

2.3 游程性

序列中连续出现0或1的子序列称为游程，连续的0或1的个数称为游程长度，游程特性是表征序列随机特性的一个重要方面。在n级的m序列的每个周期内，总的游程数为 2n-1，长度为k的游程占游程总数的1/2k，且在等长游程中，0游程和1游程各占一半，m序列的游程特性是非常优良的[10]。因此，可以将Gold码、Kasami小集合序列、新扩频码与m序列进行对比。

在Matlab仿真平台下，取序列的级数n＝8，将Gold码、Kasami小集合序列、新扩频码与m序列的对比如表3所示。

表3 Gold码、Kasami小集合序列、新扩频码与m序列的游程性对比（序列级数n＝8）

图7 3种扩频码的平衡度对比

由表3可以看出，新构造的扩频序列的游程长度与m序列基本一致，具有很好的游程性。

2.4 线性复杂度

在卫星导航定位系统中，对抗干扰和抗截获的性能要求比较高，所以新构造的扩频码必须具有较高的线性复杂度，这直接关系到导航系统保密性能的优劣[11]。一般来讲，对于长度为N的序列，线性复杂度为N/2时，序列的安全性最好。所谓线性复杂度就是利用线性反馈移位寄存器去恢复该序列的难易程度。例如，设α=(a0，a1，…，aN-1)是一个长度为N的序列，那么该序列的线性复杂度就是能够生成该序列的最短线性反馈移位寄存器的级数。1967年，Berlekamp发现了一个BCH译码算法，到了1969年Massey将该算法成功应用于线性反馈移位寄存器的重构问题，提出了著名的Berlekamp-Massey算法，简称为B-M算法。B-M算法的基本思想是对序列求n=0，1，2，…，N-1的线性反馈移位寄存器＜fn(x)，ln＞，当＜fn(x)，ln＞等于＜fn+1(x)，ln+1＞时，序列的线性复杂度为ln。具体算法如下：

设序列a0，a1，a2…，aN-1是有限域上GF(q)上的一个任意给出的长为N的有限序列。对n用数学归纳法来定义一系列的＜fn(x)，ln＞，n=1，2，3，…，N。① 设n0是非负整数使：a0=a1=a2=…=an0-1=0，an0≠0，约定：d0=d1=d2=…=dn0-1=0，dn0=an0，并令：f1(x)=f2(x)=…=fn0(x)=1,l1=l2=…=ln0=0，同时可以任取一个n0+1，线性移位寄存器作为＜fn+1(x)，ln+1＞。为确定起见，令：fn0+1(x)=1-dn0xn0+1，l=n。n0+10+1② 设，i=1，2，…，n(n0＜n＜N)已经求得。而：l1=l2=…=ln0＜ln0+1＜ln0+2≤…≤ln，另：fn(x)=1+cn1x+cn2x2+…+cnlxln，计算：dn=an+cn1an-1+cn2an-2+…+cnlnan-ln。dn为第n步的差值，区别下面两种情况：1）dn=0，这时令fn+1(x)=fn(x)，ln+1=ln；2）dn≠0，这时取m(1≤m＜n)使lm＜lm+1=lm+2=…=ln，并令fn+1(x)=fn(x)-，ln+1=max{ln，n+1-ln}。最后，得到序列a0，a1，a2，…，aN-1的一个最短线性移位寄存器＜fn(x)，ln＞。

B-M算法流程图如图8所示，其中，ln表示序列的线性复杂度，fn(x)表示移位寄存器的状态，dn表示第n步的差值。

根据B-M算法，比较m序列、Gold码、Kasami小集合序列、新扩频码4种序列的线性复杂度，结果如表4所示。

表4 m序列、Gold码、Kasami小集合序列、新扩频码线性复杂度对比

由表4可以看出，相比较于其他3种扩频码，新构造的扩频码的线性复杂度更接近N/2这一指标，序列具有较高的安全性。

3 新扩频码误码性能仿真分析

为了全面评估新扩频码的性能，本节利用Matlab软件对基于DS-CDMA系统进行建模，分别在加性高斯白噪声信道和瑞利衰落信道下，仿真分析Gold码、Kasami小集合序列以及新扩频码的误比特率。

3.1 系统建模

假定系统的发射端与接收端实现载频完全同步，发射端与接收端的扩频码序列的产生也实现完全同步，只考虑高斯白噪声和多径衰落对DS-CDMA系统误码性能的影响[12]。在Matlab仿真平台下搭建DS-CDMA系统，其系统原理图如图9所示。

图8 B-M算法流程图

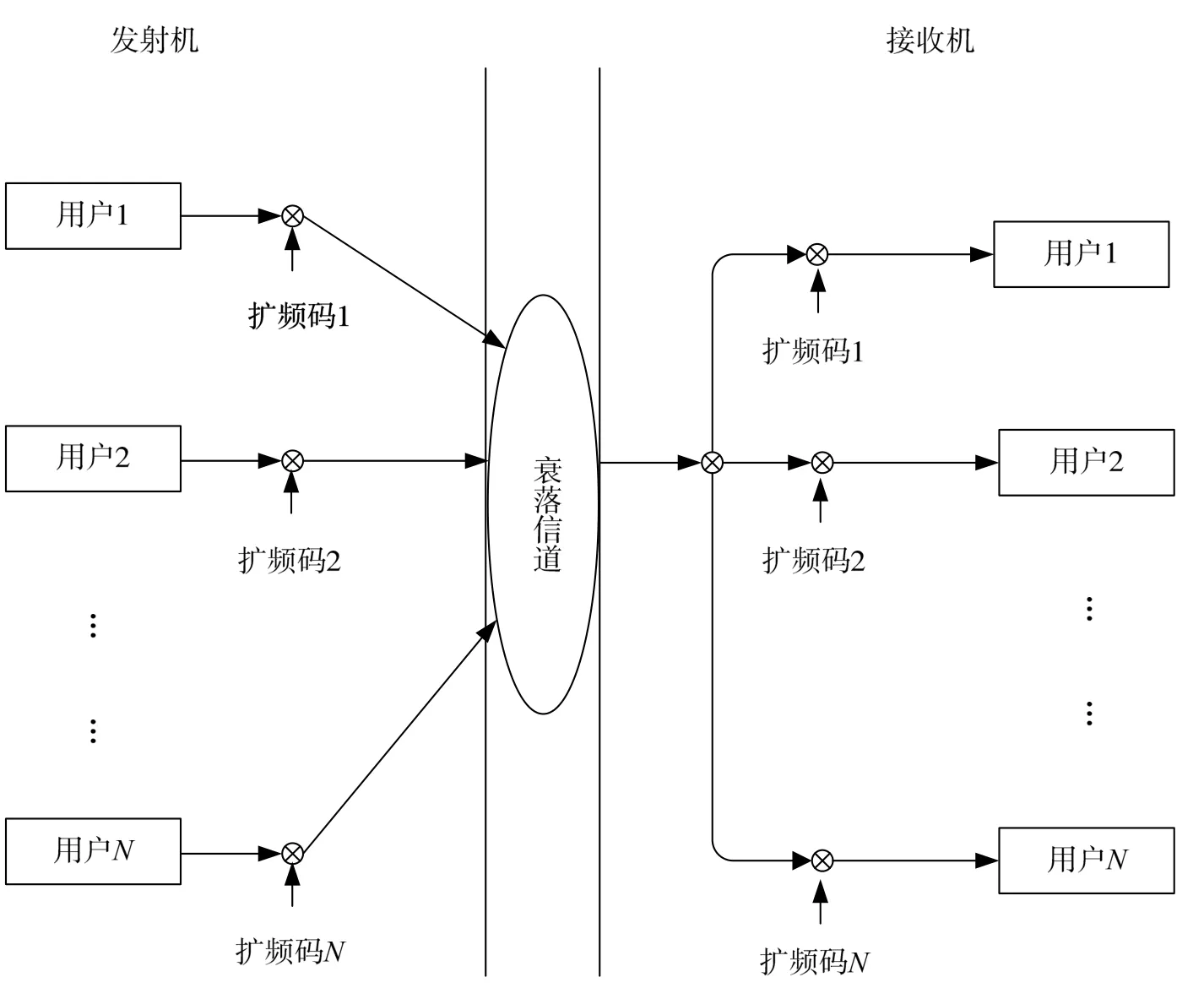
图9 DS-CDMA系统原理图

3.2 加性高斯白噪声信道的误码性能

AWGN信道是通信系统中最基本的信道，在AWGN信道中只考虑加性高斯白噪声对传输信号的影响[13]。在Matlab仿真平台下，分别仿真分析Gold码、Kasami小集合序列以及新扩频码应用于DS-CDMA系统中时，其在AWGN信道下的误比特率。如图10所示，图中扩频码长度为63，信噪比变化范围为0～10 dB，用户数为4，发射数据进行Gray编码并进行4-QAM调制。

图10 当用户数为4时3种扩频码在AWGN信道下的性能表现

由图10可以看出，信噪比相同的情况下，Gold码性能最佳，Kasami小集合序列性能最差，新扩频码性能介于两者之间。当信噪比大约大于6.8 dB时，Gold码的误比特率小于10-3；当信噪比大约大于8 dB时，新扩频码的误比特率小于10-3；当信噪比大约大于9 dB时，Kasami小集合序列的误比特率小于10-3。综上所述，在AWGN信道下，Gold码性能最优，新扩频码次之，Kasami小集合序列最差。

3.3 瑞利衰落信道的误码性能

在卫星导航定位系统中，导航信号传播的环境是复杂多变的，存在多径衰落现象[14]。所谓多径衰落，是指接收机收到经折射、反射和直射等几条路径到达的信号，这些不同路径到达的信号相位不一致且具有时变性，接收信号将被增强或者削弱。多径衰落的信号包络的浮动服从瑞利分布，传输路径中相位变化服从均匀分布，我们将此多径衰落称为Rayleigh衰落[15]。本文利用改进的Jakes模型来产生单径的平坦型Rayleigh衰落信道。在Matlab仿真中，假定各用户信号经过5条路径到达接收端，每条路径由6个或7个平面波叠加产生Rayleigh衰落波形，扩频码序列长度为63，同时传输的用户数为4，信噪比变化范围为0～10 dB，在Rayleigh衰落信道加AWGN信道情况下，DS-CDMA系统的误码性能分析如图11所示。

由图11可以看出，信噪比相同时，新扩频码的误码性能最佳，Kasami小集合序列的误码性能最差，Gold码介于两者之间。当信噪比大于2 dB时，新扩频码的误比特率小于10-1，而Gold码和Kasami小集合序列的误比特率大于10-1。随着信噪比的增加，新扩频码的误比特率下降明显，当信噪比等于10 dB时，新扩频码的误比特率接近10-2，优于Gold码和Kasami小集合序列。

4 结语

本文提出了一种新的扩频码，在相关性、平衡性、游程性、线性复杂度4方面与传统扩频码进行了对比分析。结果表明：新扩频码具有优良的自相关性和互相关性；平衡性与Gold码基本一致，比Kasami小集合序列有一定改善，序列级数分别为4、6、8、10时的新序列的平衡度比Kasami小集合序列的平衡度分别改善了7.65%、11.87%、11.97%、10.03%；保持了较好的游程性；线性复杂度比传统扩频码更加接近理想设计，理想指标N/2，解决了传统扩频码线性复杂度不足的问题。利用Matlab仿真平台，搭建了加性高斯白噪声信道和瑞利衰落信道下的多用户DS-CDMA系统，对新扩频码的误码性能进行了仿真分析，结果表明：在两种信道下，新扩频码具有较低的误比特率，抗噪声性能优异。总而言之，新扩频码本身具有一定的优势。

图11 当用户数为4时3种扩频码在Rayleigh衰落信道下的性能表现