基于Chirp信号的BPM短波数据调制研究

袁江斌，华宇，李实锋，闫温合，高媛媛1

（1.中国科学院 国家授时中心，西安710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安710600；3.中国科学院大学，北京100049）

0 引言

鉴于BPM短波授时系统具有作用距离远、接收设备简单、价格低廉以及拥有战时顽存性等优点[1-2]，若利用该系统开展数据广播业务，可以尝试在时频体系中多系统之间的数据共享、物联网低轨卫星历书广播等方面推广应用，同时对推动我国短波授时技术的发展具有重要意义。目前，BPM短波授时系统在5 MHz发播频点上以实验形式发播的时码信息主要包括基本时间信息（年、月、日、时、分）、DUT1、闰秒预告等[3]。现有时码发播实验方案存在的主要问题[4]：①数据率低，只有1 b/s，发播一个完整的时码信息需要1 min，受到短波信道干扰的风险很大；②时码帧格式中没有足够的预留扩展位，难于实现系统扩展应用；③没有可靠的校验，接收终端难于判断接收时码信息的准确性。为此，本文将Chirp信号作为数据调制信号应用于BPM短波授时系统中，试图解决其无法提供可靠数据服务的缺陷。作为一种独特的扩频技术，Chirp信号具有大时宽带宽积、低功耗以及良好的抗多径衰落、抗多普勒频移等优点，学者们针对Chirp信号在通信系统中的应用，已展开深入的研究[5-11]，主要集中在基于Chirp信号调频率的键控调制及多址通信和基于分数阶傅里叶变换法解调等方面。采用二进制Chirp信号调频率键控（Chirp-rate shift keying，CrSK）调制时，增加数据率将压缩调制符号的码元长度，当其与短波信道中最大多径时延相当时，极易引起符号间干扰。采用多进制CrSK调制时，接收终端需要比较精确的同步才能够解调[7]，这对短波用户而言难于实现，并且随着进制数的增加，调制符号间的干扰愈发严重，进而降低解调性能。

针对上述情况，考虑到MFSK具有抗干扰能力强、不受信道参数变化影响等优点，本文将Chirp信号与MFSK结合起来，形成多进制Chirp信号中心频率键控（multiple chirp frequency shift keying，MCFSK）调制。此外，为了提高带宽效率，将MCFSK与二进制Chirp-rate键控进行级联，最终形成MCFSK-2CrSK（简记为MCFrSK）调制方式用于实现BPM短波授时系统中的数据调制。

1 基本概念

本节主要分析表征Chirp信号抗干扰信号能力和抗多径衰落能力的两个重要参数以及Chirp信号中心频率的检测方法，为后续基于Chirp信号的数据调制与解调的研究奠定基础。

1.1 Chirp信号的两个重要参数

考虑如下式所示的Chirp基带信号：

式（1）中：-Tc2≤t≤Tc2，Tc表示信号时长；fi为中心频率；K为调频率。fi与fi+1之间的差值记为Δf，即Δf=fi-fi+1。规定Δf＞0。令Bc=K·Tc、GI=Bc·Tc分别表示该Chirp信号的带宽和脉冲压缩比。假设短波信道中存在一时延为τ的多径信号，如下式所示：

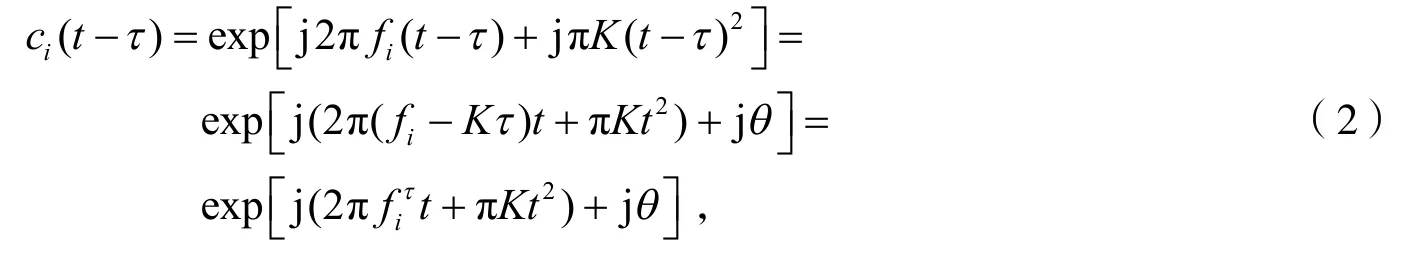
1.2 基于Chirp-傅里叶变换的频点检测原理

定义一个与式（1）所述的基带信号相匹配的乘积因子φ-K(t)=exp(-jKπt2)，将接收基带信号与φ-K(t)相乘，并对乘积结果作傅里叶变换（Fourier transform，FT）运算，如下式所示：

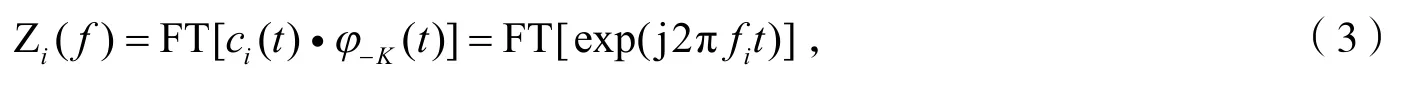
式（3）中，FT(·)表示傅里叶变换。Zi(f)即为Chirp信号ci(t)的Chirp-傅里叶变换（Chirp-Fourier transform，CFT）。求Zi(f)包络得到，其中δ(·)为狄拉克δ函数。因此，中心频率为fi的Chirp信号的CFT域与频率为fi的正弦信号的傅里叶变换域相同。利用这一特性，为基于Chirp信号中心频率键控调制的解调提供一种思路。

2 兼容性设计

增加新体制信号（包括调制信号和秒同步信号）须不影响原授时发播和用户使用。为此，本文提出在UTC/UT1时号（包括秒信号和分信号）后续部分插入新体制信号，如图1所示。图中TU表示UTC/UT1时号所占的时间，由于UTC/UT1整分信号时长为300 ms，故设计为300 ms；TG为隔离时间间隔，消除对原短波用户的干扰，设计为100 ms；TS为新体制下秒同步信号（有待进一步研究）所占时间，用于实现新体制下的秒同步，设计为80 ms；TA为新体制下的调制信号所占时间，设计为420 ms，即数据调制信号所占的总时长不得超过TA。另外，为了满足现有带宽要求，新体制下，系统可用带宽B设计为8 kHz。

图1 兼容设计示意图

3 基于Chirp信号的数据调制方法

MFSK具有抗干扰能力强、不受信道参数变化影响等优点，将Chirp信号与MFSK结合起来，形成多进制Chirp信号中心频率键控调制（MCFSK）方式，不仅保留了MFSK的优点，而且还能够进一步提高系统数据传输的抗信道干扰能力。此外，将MCFSK与二进制Chirp-rate键控（记为2CrSK）相结合，形成MCFSK-2CrSK的级联调制（简记为MCFrSK），可在不改变MCFSK调制信号的带宽前提下，进一步提高系统数据传输率。将MCFrSK的调制数记为M，并定义如下所示的 2M×的矩阵M：

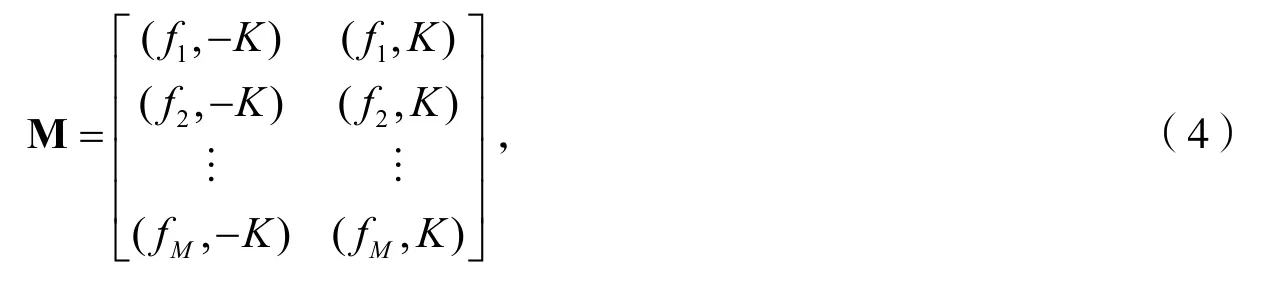
根据式（4），MCFrSK调制信号可表示为：

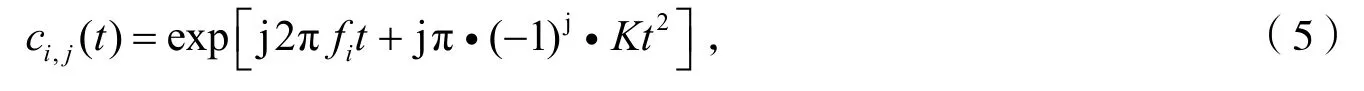
式（5）中，1≤i≤M，1≤j≤2。

3.1 MCFSK基本参数设计

短波电离层多径模式有两种形式[12]：一种是由电离层不均匀体所引起的传播时延差小的多径；另一种是由不同跳数的射线、高仰角和低仰角射线等形成的传播时延差较大的多径。

针对第一种多径情况，以Δf为间隔，均匀划分M-2个中心频率，即f1-fM=(M-1)Δf。根据线性调频信号的特点，如图2所示，当f1=B2-Bc2、fM=Bc2-B2时，能够保证在满足系统可用带宽B的基础上，使cB达到最大值，进而使多径分辨能力最强，进而降低由多径干扰导致接收信号衰落的风险。此时，容易得到：

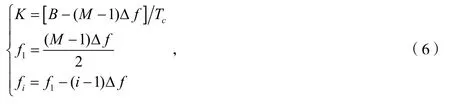
式（6）中，2≤i≤M，并且要求Δf＜B(M-1)。

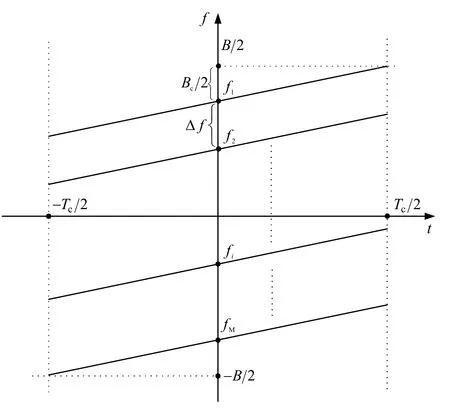
图2 Chirp信号中心频率的划分

针对第二种多径情况，假设信道中存在一个有效的最大多径时延τmax，并假定载波频差为±fd，规定fi的判决域为Di=[fi-fd，fi+fd]，根据式（2），信号时延（含同步误差）会引起中心频率变化，此时，可能存在一干扰频点，为了避免该频点对解调判决造成误判，如图3所示，要求，即要求Δf≥τmaxK+2fd，取边界值，并将其代入式（6）中，容易得到：

式（7）中，a=Tc/τmax。再将式（7）代入式（6）中可求得调频率K和中心频率fi。

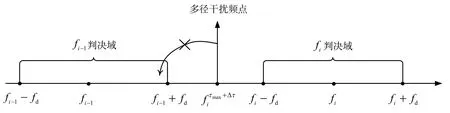
图3 MCFSK频点检测示意图

需要指出的是，将MCFSK与二进制Chirp-rate键控进行级联调制的信号中心频率、调频率数值和带宽与MCFSK调制相同。因此，MCFrSK与MCFSK基本参数的设计方法一致。

3.2 基本帧设计

BPM短波授时系统主要的数据业务包括：①基本时间信息（年、月、日、时、分、秒）；②辅助信息，包括DUT1、闰秒、闰秒提示以及用于扩展系统应用的预留信息。根据业务类型，设计两种基本帧：基本时间信息帧、辅助信息帧。两种基本帧的总比特数一致，由1比特的帧类型识别码、8比特的CRC校验码和不少于32比特的有效信息组成。因此，基本帧的总比特数不得小于41。

3.3 MCFr SK参数计算

短波信道不仅存在由多径效应引起的频率选择性衰落，还存在由电离层多普勒效应引起的时间选择性衰落[13]以及大量的干扰信号[14]。时间选择性衰落程度与信号持续时间有关。因此，信号的时长、带宽和脉冲压缩比是衡量MCFrSK调制应用于短波信道中的重要参数指标。本节根据不同数据率需求计算这些参数。

式（8）中，［·］int表示向下取整。TA内包含MCFrSK调制信号的个数为［TATc］int。令m=［TATc］int，则有：

并且有′=m·Tc。假设基本帧的比特数为Fb。根据第3.2节的分析，Fb≥41。显然，Rb的数值大小与Fb呈倍数关系，即Rb=n·Fb，其中n表示1 s内可传输的基本帧的帧数。因此，可以得到：

将修正后的中心频差Δfadj代入式（6）中并经过适当变换便可得到信号的带宽和脉冲压缩比，如下式所示：

3.4 MCFr SK调制方式选择

为了降低成本，短波用户接收机使用的本地晶振性能不会太好。以常温晶振为例，其输出的频率稳定度一般为1～10 ppm，假设标称频率为10 MHz，则其输出的频率误差最大可达100 Hz。另外，尽管短波信道中多径干扰比较严重，但在实际工程上，只考虑多径时延差在3 ms以内的多径干扰信号。因此，可令信道中可能存在的最大多径时延τmax=3ms、载波频差fd=200Hz（可获取一定的冗余），根据3.3节的分析，通过｛M，n｝不同组合，计算得到相应的MCFrSK调制参数，如表1所示。

表1 MCFrSK调制参数

根据表1计算结果，在同一数据率下，兼顾多径分辨率、脉冲压缩比等参数综合考虑，可以确定调制数M的最佳取值为2。因此，本文选取2CFrSK（简记CrFSK）作为基于Chirp信号的BPM系统数据调制。

4 CFr SK解调方案

采用Chirp-傅里叶变换法进行解调时，仅需要两路CFT检测器对基带输入信号进行检测，一路将输入基带信号与匹配因子φ-K(t)=exp(-jKπt2)相乘，然后进行FFT（fast Fourier transform）运算；另一路将输入基带信号与匹配因子φK(t)=exp(jKπt2)相乘，并进行FFT运算。采用分数阶傅里叶变换法解调也是一种不错的选择，但相比于CFT，分数阶傅里叶变换在DSP、FPGA等器件上缺乏成熟可靠的快速实现方案。因此，本文采用CFT对CFrSK进行解调，基本原理如图4所示。

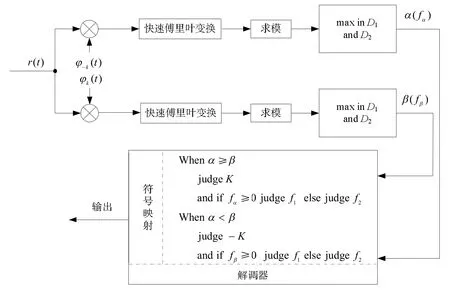
图4 基于CFT的解调原理图

根据第3.1节，可知f1=-f2＞ 0，并可确定fi的判决域Di。基于CFT的解调流程概述如下：

①将输入基带复信号r(t)分别与匹配因子φ-k(t)、φk(t)进行复乘形成两路CFT，并在判决域D1与D2中求两路CFT幅度谱的最大值及对应的频点，得到a(fa)和β(fβ)，其中a和β表示最大值，fa和fβ表示最大值对应的频点；

②将a(fa)和β(fβ)送至解调器进行解调判决：当a≥β，表明匹配因子φ-k(t)与CFrSK匹配，故可判决CFrSK的调频率为K，此时，若af≥0则可判决CFrSK的中心频率为1f，否则中心频率判决为 2f；同理可对aβ＜的情况进行调频率与中心频率的判决；

③根据判决结果，通过解调器中的符号映射进而实现数据解调。

5 仿真分析

本节使用Matlab软件自带的Awgn函数仿真模拟高斯信道以及rayleighchan函数仿真模拟短波时变多径信道，并根据文献[15]对该信道参数进行设置：多普勒谱设置为doppler.bigaussian；多径时延设置为0，10，35，120，150，200和500μs，对应的平均功率设置为0，-1，-1，-3，-3，-4和-8 dB。

在高斯信道和时变多径信道中对本文提出的CFrSK调制和现有数据调制（简称为现调制）进行误码率性能仿真比较，如图5、6、7所示。本节所述的信噪比是指解调器输出端的比特信噪比。根据仿真结果，总体上看，CFrSK调制的误码率性能明显优于现调制，具体表现在以下几个方面：

①数据率方面，CFrSK调制的最小数据率是现调制的42倍。在传输等量信息的情况下，CFrSK调制信号受到干扰的风险明显小于现调制信号；

②高斯信道下，以要求误码率不得大于10-3为例，CFrSK解调信噪比性能比现调制信号提高了6 dB（不考虑扩频增益）；

③时变多径信道下，随着信噪比的增加，现调制误码率性能改善程度明显小于CFrSK调制。特别是当多普勒频移较大时，如图7所示，现调制信号无法实现可靠的数据传输。

综上所述，本文提出的2CFrSK调制在数据率、高斯信道误码率性能、时变多径信道误码率性能方面均明显优于现有数据调制方案。

此外，通过仿真结果，还可得到以下几个结论：

①高斯信道下，不同数据率情况下CFrSK的解调误码率性能一致；

②时变多径信道下，数据率越小，CFrSK解调误码率性能越好。这是由于数据率越小，CFrSK信号的带宽越大、多径分辨能力越强，则抗频率选择性能衰落越强；

③当多普勒频移从0.1 Hz变化为4 Hz时，比较图6和图7发现，CFrSK调制的误码率性能曲线变化不大，充分表明CFrSK调制具有良好的抵抗时间选择性衰落的特性。

根据上述结论，并兼顾抗短波信道中的窄带干扰能力，数据率的选择，需要与带宽或多径分辨率、脉冲压缩比之间折中考虑。本文选用数据率为82 bit/s的CFrSK作为BPM系统的数据调制。当然最佳数据率的选取有待在实际工程中进一步验证。

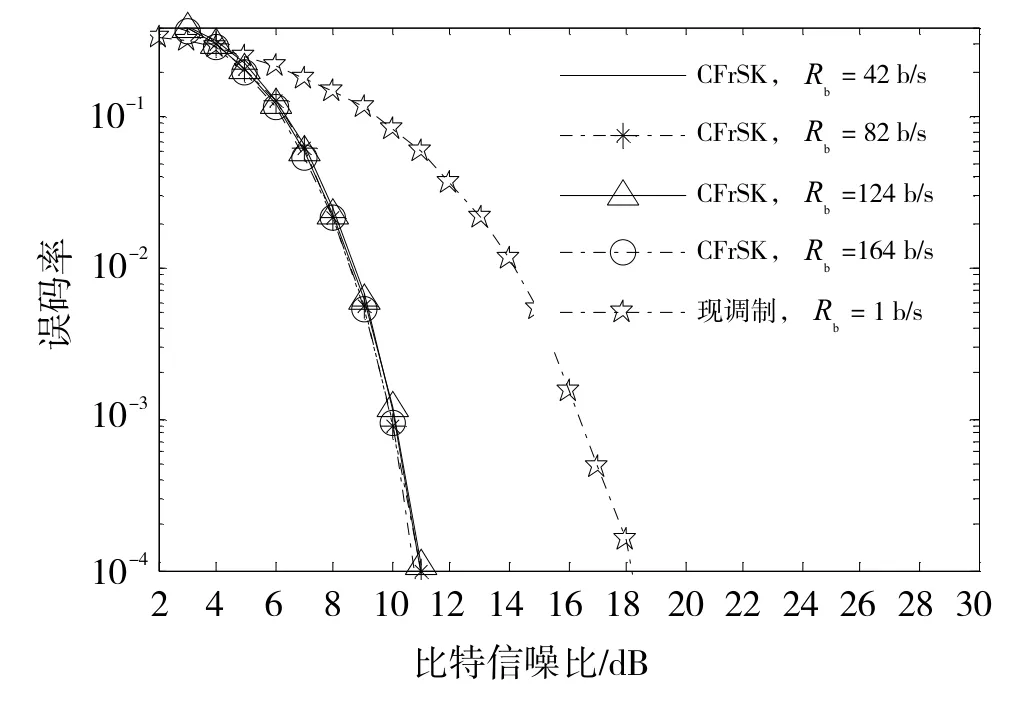
图5 高斯信道下的误码率性能

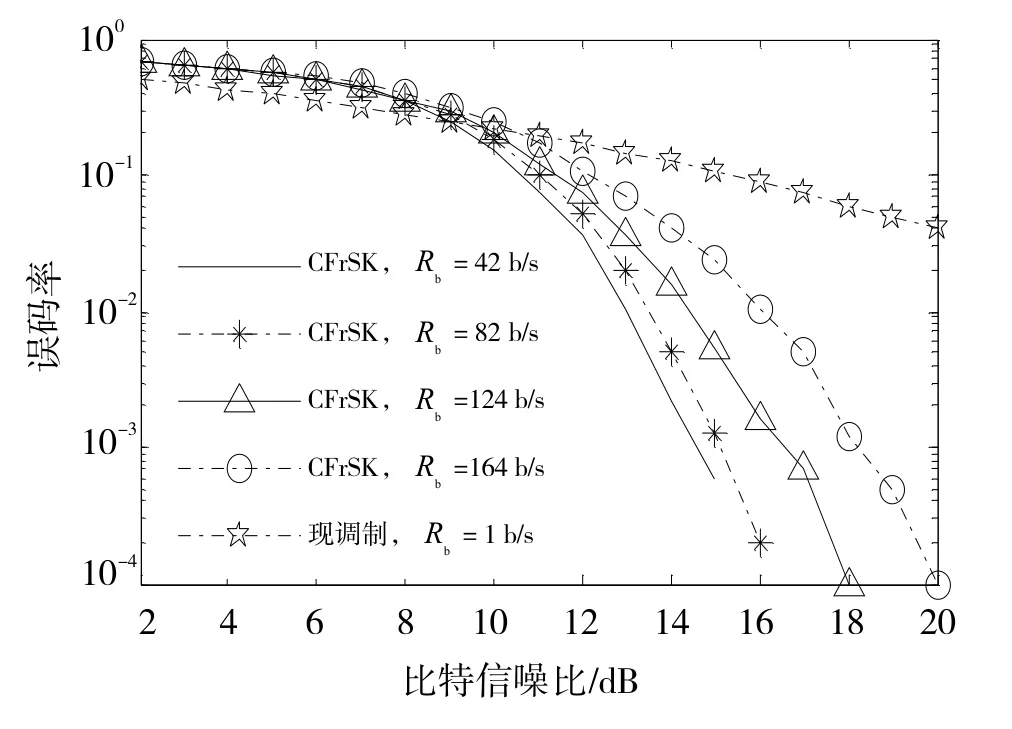
图6 多普勒移为0.1 Hz的时变信道下误码率性能

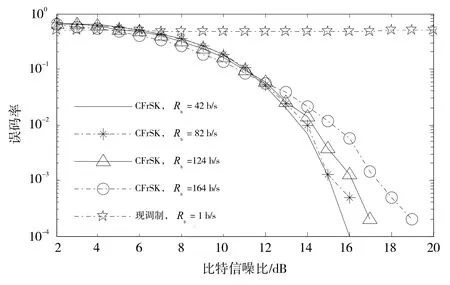
图7 多普勒移为4 Hz的时变信道下误码率性能

6 结语

针对BPM短波授时系统存在无法提供可靠数据服务的缺陷，本文研究了基于Chirp信号的数据调制方法，该方法为BPM短波授时系统实现数据广播业务提供理论依据，对推动短时授时技术的发展具有积极意义。首先根据现有体制信号格式，提出了一种兼容性设计方案，然后提出了Chirp中心频率键控与Chirp-rate键控进行级联作为BPM的数据调制方法。此外，为了验证本文提出的调制方法的性能，提出了一种低复杂度解调方案，该方案可使用FFT实现基于Chirp-Fourier变换的快速解调。本文提出的调制方法可将数据率从原1 b/s提升到82 b/s，在传输等量信息情况下，可显著降低信号受信道干扰的风险，同时还具有18 dB的抗干扰增益和172μs的多径分辨率。仿真结果表明，本文提出的调制方法在高斯信道误码率性能、时变多径信道误码率性能均明显优于现有数据调制。基于本文的研究，可为我国BPM短波授时系统的后续技术升级改造提供理论参考。