基于Hilbert变换的数字鉴相器研究

李兴林，刘军良，赵当丽，关小龙

（1.中国科学院 国家授时中心，西安710600；2.中国科学院 时间频率基准重点实验室，西安710600；3.中国科学院大学，北京100049）

0 引言

鉴相技术在通信、测距、测向、鉴频、电机控制等多个领域都有广泛的应用[1]，在射电天文学、高速数字通信、高精度时间同步等科学技术领域中，使用鉴相技术进行频率稳定度测量也十分重要。在时频领域中，新型的原子钟、喷泉钟、光钟等因具有很高的频率稳定度因而被广泛地作为频率源。商用原子钟的频率日稳定度在10-13～10-16之间，例如在甚长基线干涉仪进行天体测量时，使用氢钟作为时钟源，当τ=1 ks时频率稳定度的要求为σν(1ks)=10-15[2]，另外现代工业化进程伴随着的高速度交通工具、深空探索、精密导航定位需求等也对时间频率的高精度测量提出了更高的要求[3]，因此对频率稳定度分析的新技术研究具有重要的现实意义。高精度频率源的测量常使用双混频时差测量法，先对信号混频然后过零检测，过零点触发计数器进行测量，但过零点容易受到噪声污染导致测量出现误差，为避免过零检测带来的噪声污染，实现高精度频率稳定度的测量，本文根据Hilbert变换原理，分别采用窗函数法和等波纹切比雪夫法设计FIR（finite impulse response）型Hilbert滤波器，来产生I、Q支路，再通过反正切运算求出相位进而可以计算频率稳定度。

1 基于Hilbert变换的数字鉴相器的设计原理

基于Hilbert变换的数字鉴相器的设计核心是Hilbert滤波器的设计，利用Hilbert滤波器产生I、Q支路，通过反正切运算求出相位。

1.1 Hilbert变换的定义

设(x)t为原子钟输出的连续时间信号，其Hilbert变换(t) 定义为[4]

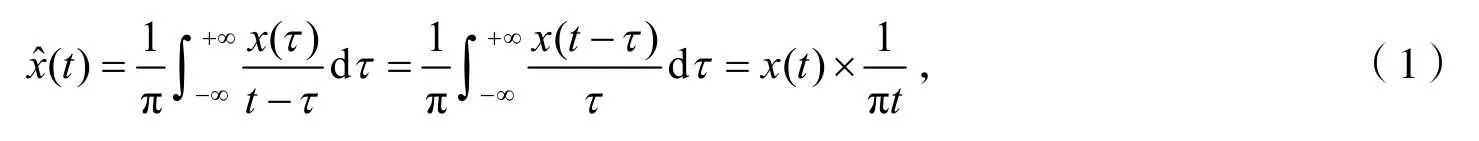
式（1）中，τ为时间变量，连续时间信号x(t)的Hilbert变换可以看成x(t)通过具有冲击响应为h(t)=1πt的线性滤波器。本文所设计的鉴相器的Hilbert滤波器的频率特性为[5-7]

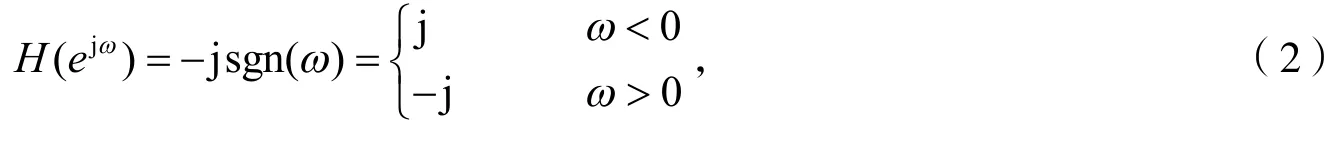
式（3）中，(φ)ω为相频响应函数，ω为频率（或角频率），由此可见信号x(t) 的Hilbert变换可以看成是信号x(t) 通过一个幅度为1的全通滤波器输出，其负频率成分作+90°相移，而正频率成分作-90°相移，而不改变频谱分量的幅度。其幅频特性和相频特性如图1所示。

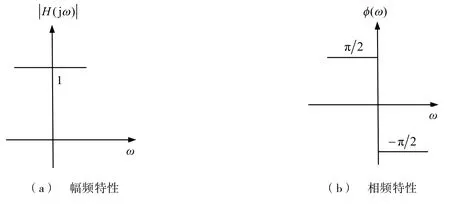
图1 幅频特性和相频特性

例如：信号sin(2×π×10×t)通过Hilbert变换，将变为信号-cos(2×π×10×t)，其仿真图如图2所示。

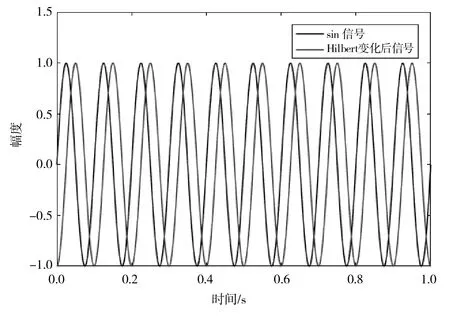
图2 sin(2×π×10×t)Hilbert变换仿真

1.2 系统的原理框图

基于Hilbert变换的数字鉴相器的原理框图如图3所示。

图3 Hilbert变换的数字鉴相器的原理框图

输入信号分成两路，一路通过 12N阶Hilbert滤波器产生Q支路，另一路进行 1N采样延时产生I支路。即对信号进行希尔伯特变换就相当于对该信号进行正交移相，产生的I，Q支路，使它成为自身的正交对，然后再对产生的I，Q路通过反正切运算求出相位。

2 FIR型Hilbert数字滤波器的设计

Hilbert滤波器可以分为FIR型和IIR（high response）型，FIR型数字滤波器和IIR型数字滤波器相比较有以下优点[8-10]：

①FIR型数字滤波器可以实现严格的线性相位，而IIR型数字滤波器要实现严格的线性相位，就会导致选择性变差。

②FIR数字滤波器主要采用非递归的结构，因而从理论上以及在实际的有限精度的运算中，都是稳定的。IIR数字滤波器必须采用递归结构，只有极点在平面单位圆内才是稳定的，运算中的四舍五入处理，有时会引起寄生振荡。

为得到严格的线性相位，本文进行了FIR型滤波器的设计。具有线性相位FIR型数字滤波器的频率响应函数可以统一表示为

式（4）中，τ=(N-1)2为时延，N为滤波器阶数；；若k=0时，为I，II型；若k=1时，为III，IV型；Hr(ejω)为振幅响应。因为Hilbert数字滤波器的单位冲击响应是奇对称的，即k=1，其频率响应函数为

式（5）中，ω为频率（或角频率）且π-≤ω≤π。

2.1 窗函数法设计Hilbert数字滤波器

取N为奇数，所设计的Hilbert数字滤波器的理想频率响应函数为[11-14]

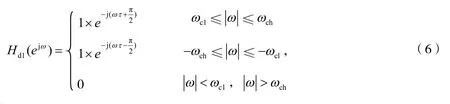
式（6）中，τ=(N-1)2为采样延时；ωc1，ωch分别为下截止频率和上截止频率。其单位冲击响应函数hd1为

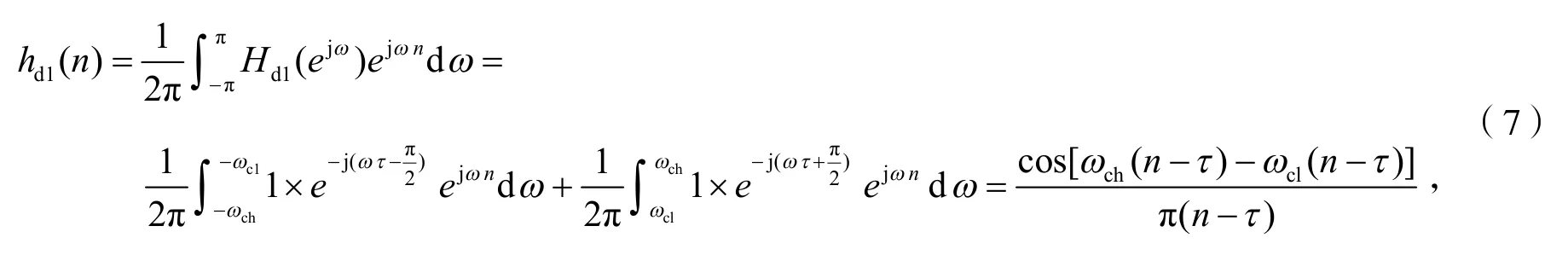
于是有

式（8）中，ω(n) 为有限长的窗口函数序列。

现设计的带通Hilbert滤波器参数为：ωs1=0.2×pi；ωp1=0.35×pi；ωp2=0.65×pi；ωs2=0.8×pi；Rp=0.003 dB；As=75 dB（ωs1，ωs2为阻带截止频率，ωp1，ωp2为通带截止频率，Rp为通带波动，As为阻带衰减），窗函数选取布莱克曼窗，窗函数法设计Hilbert滤波器的阶数N=75，其幅频特性和相频特性如图4所示。

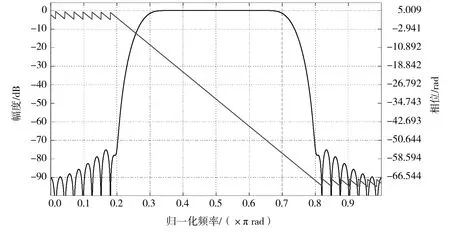
图4 窗函数法Hilbert滤波器的幅频特性和相频特性

2.2 等波纹切比雪夫法设计的Hilbert数字滤波器

等波纹切比雪夫法采用了Parks-McClellan算法，取N为奇数，所设计的Hilbert数字滤波器的理想频率响应函数Hd(ejω)同式（6），其逼近误差函数为[15-17]

式（9）中，W(ω)为逼近加权函数，H(ω)为线性相位FIR型数字滤波器的逼近函数。

令δ=max［E(ω)］，为获得最优单位冲击响应h(n)，需要寻找使δ=max［E(ω)］最小的逼近函数H(ω)，因此Hilbert数字滤波器的频率响应函数为

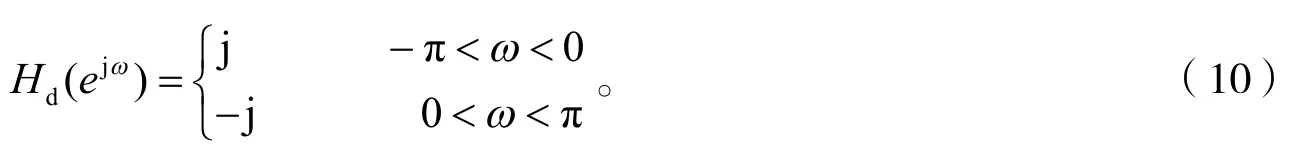
现设计带通Hilbert滤波器参数为：ωs1=0.2×pi；ωp1=0.35×pi；ωp2=0.65×pi；ωs2=0.8×pi；Rp=0.003 dB；As=75 dB（ωs1，ωs2为阻带截止频率，ωp1，ωp2为通带截止频率，Rp为通带波动，As为阻带衰减），其滤波器的参数与窗函数法设计的Hilbert数字滤波器的参数一致，等波纹切比雪夫法设计Hilbert滤波器，其幅频特性和相频特性如图5所示。

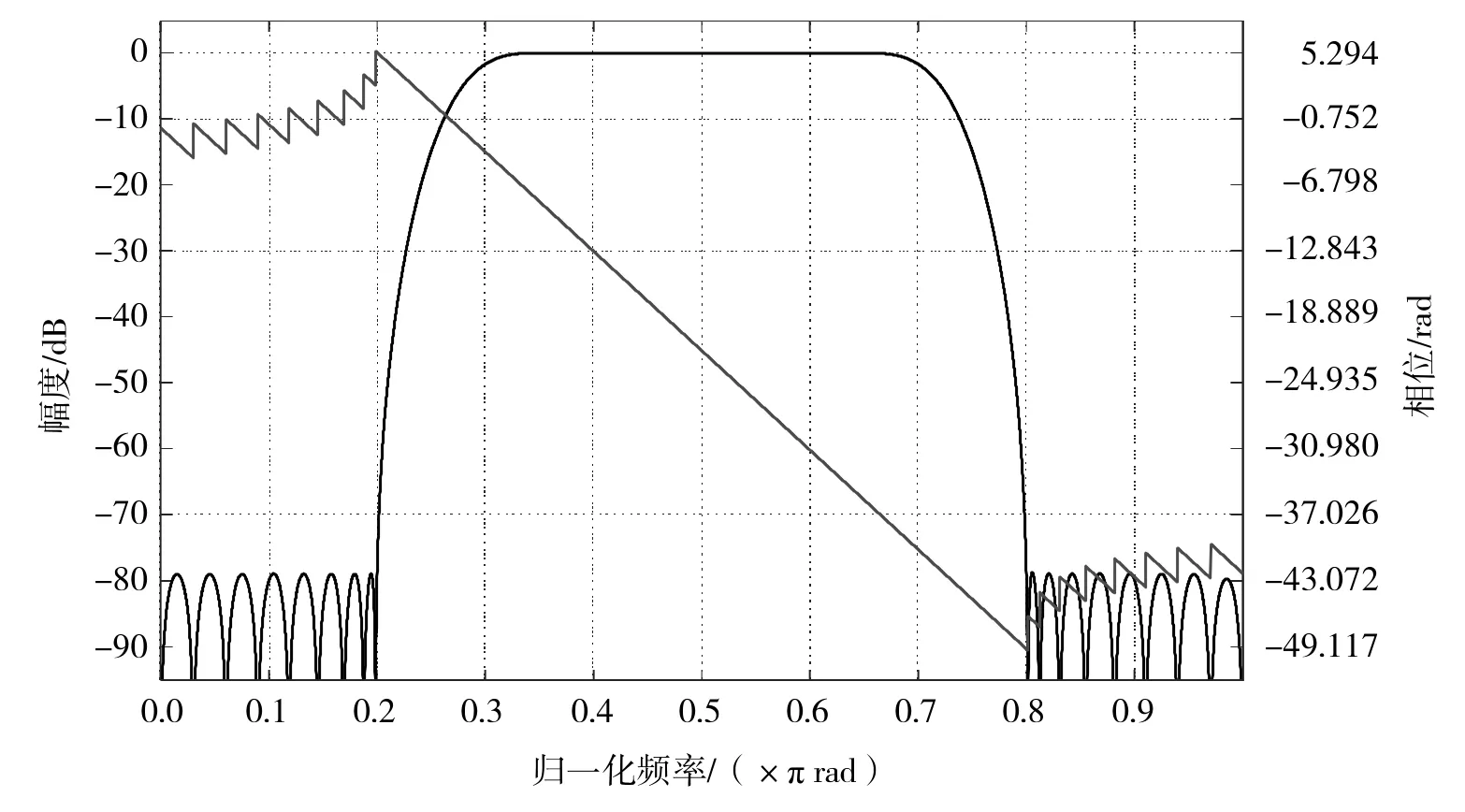
图5 等波纹法Hilbert滤波器的幅频特性和相频特性

2.3 窗函数法和等波纹法设计的Hilbert数字滤波器的比较

在2.1节和2.2节中分别采用窗函数法和等波纹切比雪夫法设计带通Hilbert滤波器，滤波器参数都为：ωs1=0.2×pi；ωp1=0.35×pi；ωp2=0.65×pi；ωs2=0.8×pi；Rp=0.003 dB；As=75 dB（ωs1，ωs2为阻带截止频率，ωp1，ωp2为通带截止频率，Rp为通带波动，As为阻带衰减），现改变两种方法设计的Hilbert滤波器的纵坐标的最小精度，对通带进行放大，如图6和图7所示。

根据图6和图7我们可以发现，窗函数的实际响应和理想响应之间的逼近误差，在全频带区间上是不均匀分布的，靠近边缘频率处误差较大，远离边缘频率处较小（Gibbs吉布斯现象），而等波纹法可以实现在全频带区间上均匀分布且逼近误差更小，进而可以用较低的阶数实现相同的技术指标。

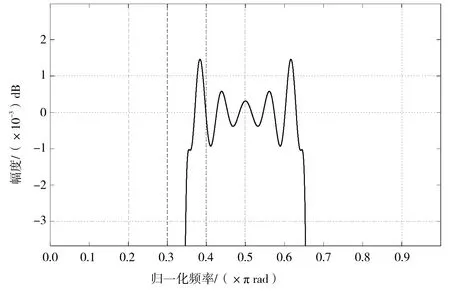
图6 窗函数法设计Hilbert滤波器

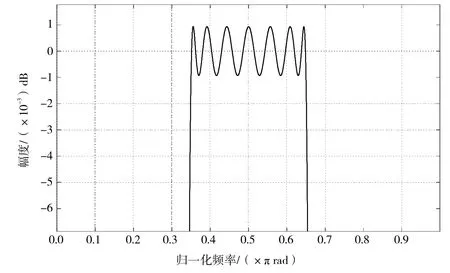
图7 等波纹切比雪夫法设计Hilbert滤波器

根据窗函数法和等波纹法设计滤波器的特点我们可以知道，窗函数法不能精确指定阻带截止频率ωs和通带截止频率ωp只能接受设计所得的大体合用值[18-19]，等波纹法可以精确指定ωs和ωp，其次窗函数设计方法中使δ1=δ2，不能同时控制波动系数δ1和δ2[20-21]。

同时在使用Matlab进行仿真时可以得到，窗函数法设计Hilbert滤波器的阶数N=75，等波纹切比雪夫法设计的Hilbert数字滤波器的阶数N=61，并且通带波动 pR=0.0019 dB，As=78 dB，可见等波纹切比雪夫法设计的Hilbert数字滤波器用更少的阶数实现了更优的设计指标，故本文采用等波纹切比雪夫法设计Hilbert滤波器。

3 系统的仿真比较

通过对频率源和系统的整体仿真，验证了系统的可行性，证明了基于Hilbert变换的数字鉴相器可实现较高的测量精度。

3.1 频率源的仿真

频率源的仿真是根据一组原子钟的典型噪声参数进行的[22]，如表1所示。

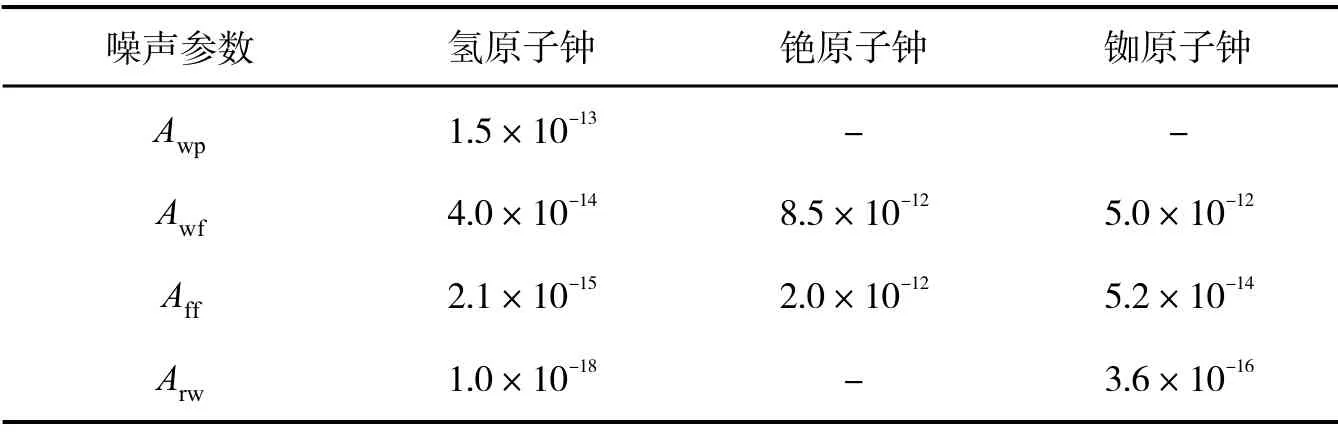
表1 一组原子钟的典型噪声参数

表1中，Awp为相位白噪声，Awf为频率白噪声，Aff为频率闪烁噪声，Arw为随机游走噪声。一般情况下，在进行钟差数据模拟时，可以忽略相位闪烁噪声[23]，现根据原子钟的噪声参数，使用Stable32软件，进行铯原子钟的频率稳定度的分析，如图8所示。

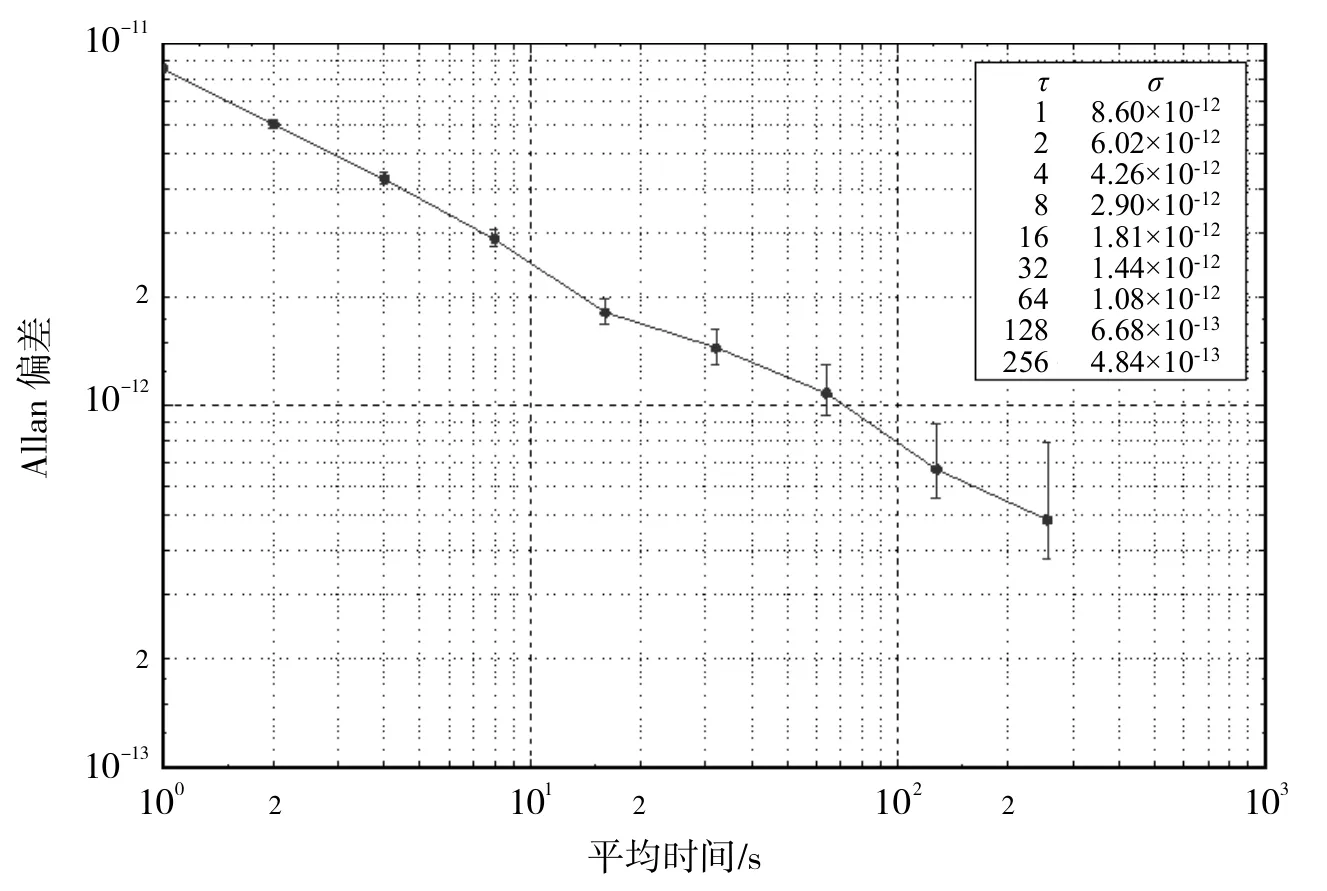
图8 铯原子钟的频率稳定度

铯原子钟部分相位数据如表2所示。

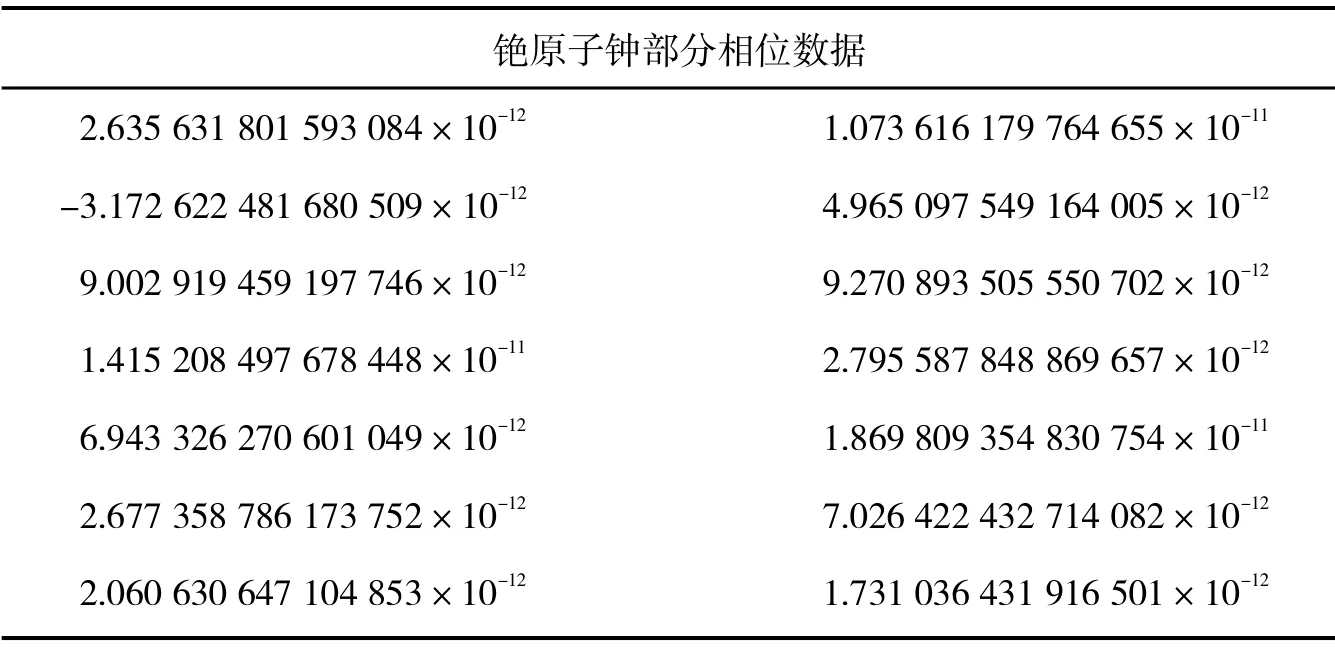
表2 铯原子钟部分相位数据 s

3.2 系统仿真过程

现设频率源为铯原子钟，其输出信号为10 MHz的正弦信号，将Stable32软件仿真的铯钟的相位数据拟合到10 MHz信号上，拟合后的信号通过Matlab进行相关处理并进行系统仿真，将系统产生的相位数据与直接使用Stable32软件仿真的铯钟的相位数据进行比较，得到输入前和输入后相位的变化。其部分比对数据如表3所示。

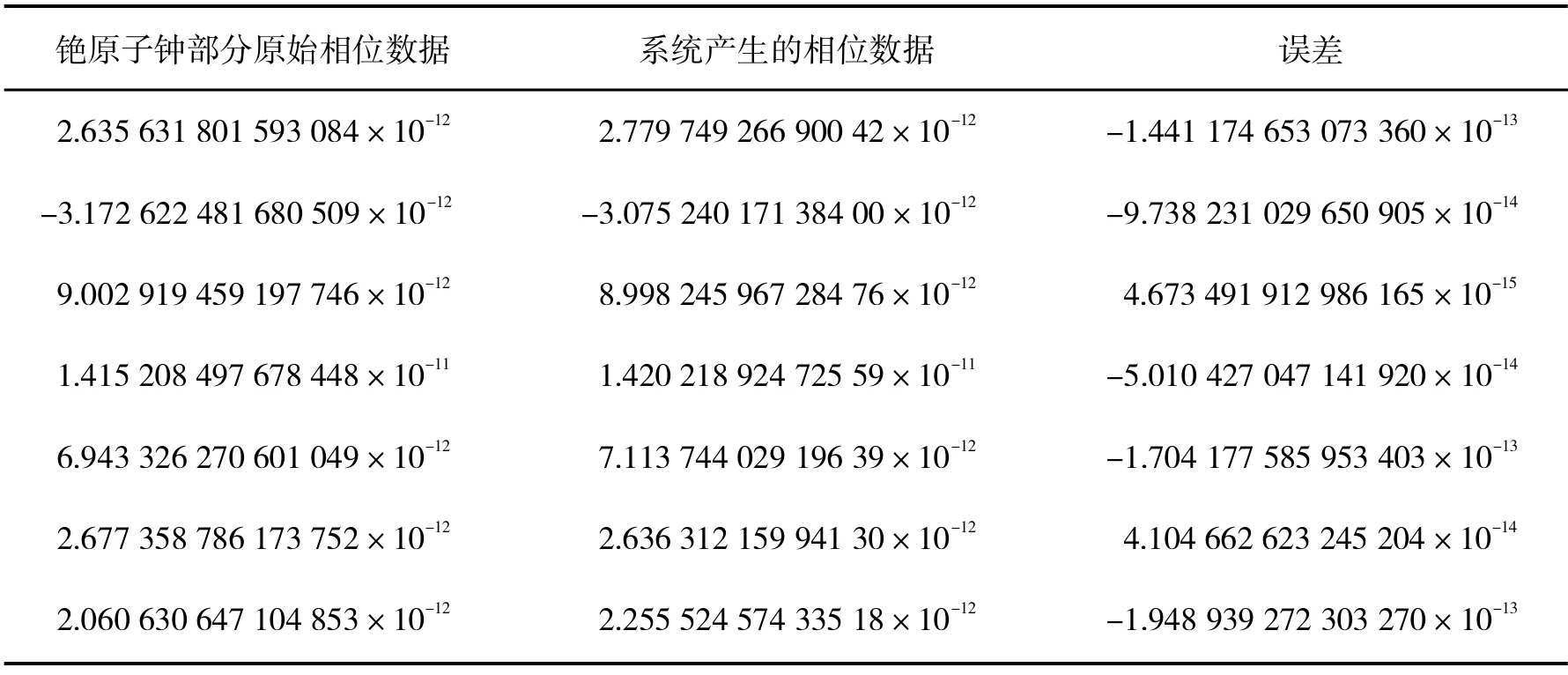
表3 铯原子钟部分比对数据 s

从表3中我们也可以看到，铯原子钟仿真原始相位数据与本文所设计的鉴相器的输出的相位数据相差较小。

用系统产生的相位数据计算频率稳定度，仿真图如图9所示。

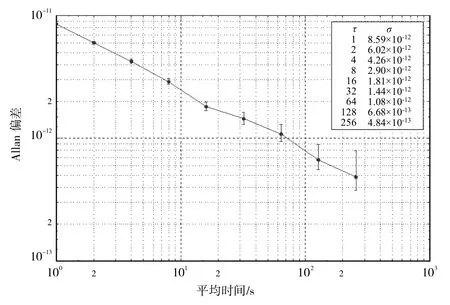
图9 系统产生的相位数据计算频率稳定度

比较图8和图9我们可以发现，铯原子钟仿真信号通过基于Hilbert变换的数字鉴相器产生相位数据，对其所产生的相位数据使用Stable32进行频率稳定度的计算，与铯原子钟仿真信号直接使用Stable32计算的频率稳定度的结果基本一致，证明了基于Hilbert变换的数字鉴相器可以实现较高的测量精度。

4 结语

本文在Matlab环境下采用窗函数法和等波纹切比雪夫法设计了FIR型Hilbert数字滤波器并对数字鉴相器进行仿真实验，证明了采用等波纹切比雪夫法设计的Hilbert滤波器较窗函数法设计的Hilbert滤波器，可以用更少的阶数实现更优的设计指标，使用Stable32进行频率源的仿真和稳定度的计算，验证了基于Hilbert变换的数字鉴相器的仿真结果，仿真结果表明利用Hilbert变换进行数字鉴相器的设计可以获得较高测量精度，验证了系统的可行性，用数字信号处理的方式代替模拟电路，避免过零检测带来的噪声污染，为后续的硬件平台的搭建提供了理论支撑。