关于圆锥面竞赛题的多解探究

王成强

(成都师范学院 数学学院，成都 611130)

大学阶段数学中的“解析几何”知识模块主要涉及借助于线性代数理论研究几何理论的学科[1,2]，它能提升学生的科学计算能力、逻辑推理能力、抽象思维能力、空间想象能力等[3]。二次曲面理论是大学阶段“解析几何”知识模块的教学重难点[1,2]。对第七届中国大学生数学竞赛非数学专业类预赛[4](2015年)第二题进行“一题多解”研究，该题内容完整表述如下：设在空间直角坐标系O-xyz中，圆锥面S经过三条坐标轴的正半轴，试确定圆锥面S的方程。

一题多解，即从多种视角出发分析并给出同一道题多种解法，在数学的学习与讲授中起着重要作用[5]。借助于一题多解的教学，能帮助学生从不同视角理解问题，培养学生的创新思维能力，形成更系统的知识体系[5]。开展“一题多解”研究与教学，对问题所承载的知识模块的学习与教学都有启发性意义[6-8]。

1 解法探析

解法1 确定准线圆方程+消除参数。

解法2 确定准线圆方程+消除非齐次项。

解法3 找出轴线+借助于圆锥面“点到轴线的距离与点到顶点的距离成定比”的性质。

因P(1,0,0)，Q(0,1,0)，R(0,0,1)都在圆锥面S上，且|OP|=|OQ|=|OR|，故圆锥面S的轴线包含于直线段PQ与PR的中垂面。因此，圆锥面S的轴线的方程为

或等价地，为x=y=z。由“点到轴线的距离与点到顶点的距离成定比”的性质可知，圆锥面S的方程为

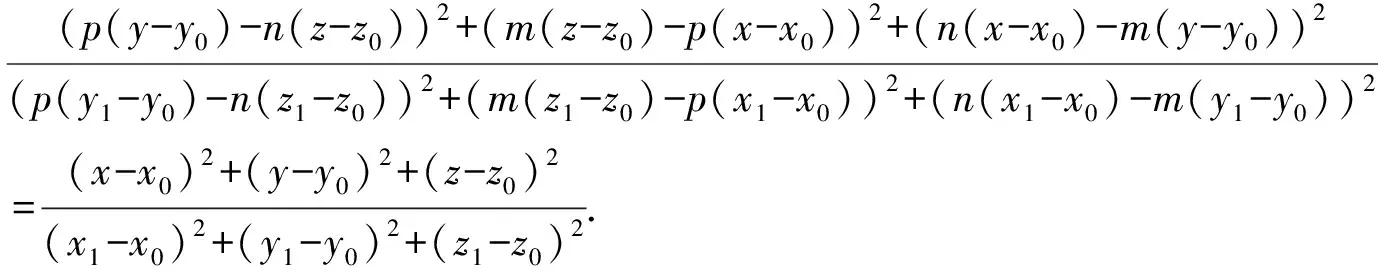
解法4 借助于注2确定圆锥面的方程。

因圆锥面S的顶点是O，轴线的方程是x=y=z，故按照注2，圆锥面S的方程为

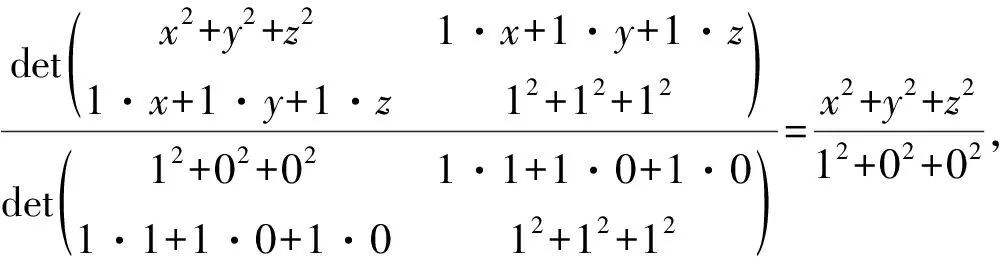
解法5 设出一般方程+列方程解出参数。

受到解法3与4，注2的启发，可假设圆锥面S的方程为

λ(x2+y2+z2)+2xy+2yz+2xz+2a14x+2a24y+2a34z+a44=0

因圆锥面S经过x轴(参数方程为(t,0,0))，故

λ(t2+02+02)+2t·0+20·0+2t·0+2a14·t+2a24·0+2a34·0+a44=0，

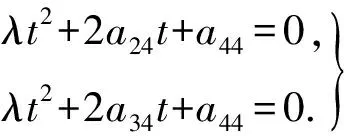
由t的任意性，有λ=0，a14=0，a24=0，a34=0，a44=0。于是，圆锥面S的方程为xy+yz+xz=0。

2 结语

第一种解法的思路来源于锥面“过定点且与定曲线相交的直线的全体”的定义。第二种解法的思路来源于“圆锥面的顶点的坐标也满足准线上的所有点都满足的齐二次代数方程”。第三种解法的思路来源于圆锥面“点到轴线的距离与点到顶点的距离成定比”的性质。第四种解法的思路本质上与第三种解法的思路一致，但用到的公式结构更便于理解记忆。第五种解法的思路是“先设出圆锥面带参数的方程+再利用题设条件列方程解出参数”。此五种解法能帮助从不同侧面更深入地认识圆锥面。