基于模型试验的桥基岸坡岩体变形分区研究

张海太 陈维 王小平

摘要 变形是控制桥基岸坡稳定性的重要因素。以西南某高速公路跨越金沙江大桥为依托，建立室内边坡模型实验及有限元模型来研究不同大小桥梁荷载作用下边坡的位移响应机制。通过定义位移敏感性系数为边坡内部各点处位移荷载曲线的平均曲率，将边坡内部划分为3种不同敏感程度区域，并与模型实验中测量得到的位移数据进行比较分析。然后基于不同荷载等级下敏感区域分布来研究桥基下方软弱夹层的存在对边坡变形的影响。结果表明：在桥梁荷载作用下，承台前缘的部分有向边坡体外部挤出的趋势，在承台处及后缘处需要考虑竖向的沉降问题。当桥梁荷载超载达到十倍设计桥梁荷载时，承台周围的位移变形已经不可忽视。下部软弱夹层的存在使桥梁荷载对边坡的影响向深处及边坡前缘发展。当桥基荷载足够大时，边坡有整体破坏的趋势。

关 键 词 桥基岸坡;模型试验;有限元;变形分区;位移阀值

中图分类号 TU457     文献标志码 A

Abstract Deformation is a key factor to control the rock stability of bridge foundation slope. In the present paper， both the laboratorial slope model and the FEM models were built to analyze the displacement response under different bridge load. The sensitive coefficient was defined as the average curvature of displacement-loading curve to partition the slope into three levels of sensitive areas and this concept was confirmed by the displacement data from laboratorial slope model test. Then， the influence of the weak layer under the bridge foundation to the deformation of slope was studied based on  different distributions of sensitive areas under different loading levels. Results show that the leading edge of bearing platform tends to be extruded out of the slope under the bridge load while the settlement  occurred both in front of and underneath the platform. When the bridge load reaches tenfold designed load， the deformation around the bearing platform cannot be ignored. And the existence of weak layer allows the bridge load to affect deep areas and leading edge of the slope. When the bridge load is extremely high， the slope tends to fail.

Key words bridge load slope; jointed finite element; deformation division; displacement threshold

在山區地带，交通线路往往穿越各种复杂地形。特别是高山河谷地段，桥梁基础被迫置于高边坡上。而桥基岸坡的岩体稳定性是工程重点关注的问题。

以应力场分析和塑性区分布作为评判桥基边坡岩体稳定性的方法，前人做了大量的研究工作。赵文等[1]、刘克玲等[2]、荆志东等[3]结合应力影响系数法及模型实验的方法研究了桥位、桥基形状等因素对边坡临界滑动面的影响;王初生等[4]探讨了用二维块体极限平衡方法计算稳定性系数的方法;董捷等[5]考虑桥基附加荷载发展了一种极限平衡方法以计算桥基边坡安全系数;詹志峰等[6]分析最大附加主应力变化曲线的变缓趋势得到桥基的合理深部位置;王春雷等[7]用数值模拟手段比较了桥基边坡二维和三维分析的差异;张雷等[8]对比了不同数值模拟方法对桥基荷载作用分析的差别;胡松山等[9]、卿笃干等[10]、邓宗伟等[11]则运用强度折减法分析了桥基荷载作用下的斜坡稳定性问题;周火明等[12]结合强度折减法、塑性区分布及结构面组合分析等几种方法综合分析桥载荷作用下桥基边坡破坏形式。然而以变形的角度研究桥基岸坡岩体稳定性的研究则较为少见。特别当变形量大小和变形区域范围发展过快时，承台附近岩体的稳定性会遭到破坏，直接影响到大桥的安全运营。因此变形能直观地反应边坡破坏的发展情况。同时，从测量的角度上来说较为方便和精确。

本文以西南某高速公路大桥桥基岸坡为背景，采用室内模型试验和数值模拟相结合的方法，提出敏感性系数的概念衡量岸坡岩体对桥基荷载变化的敏感程度，以此为依据对边坡内部进行分区，并分析下卧软弱夹层对桥基边坡变形的影响。研究结果对工程设计和稳定性加固提供重要的参考意义。

1 工程概况

西南某高速公路大桥跨越金沙江而设，路线以东西走向近垂直的角度跨越金沙江。推荐桥型方案为单跨钢桁架悬索桥。大桥主墩和锚碇分别置于金沙江两岸的斜坡中部和中上部，初步估算主墩荷载达12 万t。采用群桩承台基础，估算桩长约73 m;锚碇初步定为隧道锚，估算荷载30～40 万t。该桥跨径逾千米，其中华坪岸为顺向坡（剖面图见图1），基岩裸露受多条小型冲沟切割，岸坡上陡崖多呈三面临空姿态。

该桥基边坡除了要承受较大的桥基荷载之外，影响其稳定性的另一个重要因素在于工程区分布有由凝灰岩组成的软弱夹层，根据地质资料，凝灰岩层的走向近SN，缓倾W，倾角12°～30°。该层位在后期构造变动过程中经常会发生顺层挤压错动，并出现软化泥化现象，其强度远低于上覆的玄武岩，当这两个因素共同作用时，需要考虑在承台附近是否有变形失稳的可能。对华坪岸桥基承台稳定性的影响较大的层位主要为t2凝灰岩，也是后续分析关注的重点。

2 顺层边坡模型试验与数值模拟

2.1 静力模型试验简介

以西南某高速公路大桥顺向岸坡为研究对象，其地形受岩层结构的影响，呈陡缓交替出现的台阶状地貌，岸坡整体坡度20°～30°。利用极限平衡法搜索得到的重点区域见图2a），坡高约450 m，坡长约900 m。边坡模型的斜坡为折线坡来模拟台阶状地貌。在模型内设置贯通软弱夹层（凝灰岩夹层），模型几何尺寸相似比为1∶200。模型设计图如图2b）所示，坡高2.25 m，坡长4.50 m 。

由相似准则可知，如果两个现象相似，则这两者的无量纲形式的方程组和单值条件应该相同，具有相同的无量纲形式解。出现在这两者的无量纲形式的方程组及单值条件中的所有无量纲组合数对应相等。按照模型几何尺寸相似关系，模型材料的物理力学参数的相似计算如表1所示。

经过大量相似材料的筛选工作，最终确定采用铁粉∶重金石粉∶水∶水泥 = 30∶10∶3.5∶1.4的比例模拟玄武岩材料，采用特氟龙为凝灰岩夹层模拟材料。其材料强度以及摩擦强度见表2。

为了避免模型体积过大造成的制作不便及养护问题，同时避免模型在浇筑的过程中因浇筑时间的不同而出现材料特性差异，因此采用制作预制试块的方法来进行模型的砌筑，如图3所示。

模型砌筑方式直接关系到试验的质量，铺设过程中，应尽量避免因操作造成的不连续面，如裂缝、空隙等。砌块间采用同一材料勾缝的形式。材料在不同的养护时间其强度会有差别，因此所有的试块因同时制作、浇模、养护、铺设，铺设时间应尽量缩短。试块制作设计图如图4所示。

为了及时监测模型的对不同荷载组合的响应，对模型进行了应变、应力及变形的测试，共布置应变片120个（单向）、压力计20个（单向）。位移测量边坡顶部和侧部，采用百分表测量。

在实际设计中，主墩的基础形式为群桩承台基础。由于凝灰岩夹层的埋深较大，群桩桩身整体位于玄武岩中。而该岩层能够提供较大的摩阻力，同时岩层与混凝土的弹性模量相近。所以当桥梁荷载较小时，桩的受力形式应该以桩身摩擦力为主，且与周围岩体协调变形。在这种情况下，实验中采用直接在承台处施加均布桥梁荷载的方法来研究边坡的变形情况。本次实验中还引入超载法的概念，逐级放大桥梁荷载以找到能使边坡失稳的极限值。此时，实际的桩基受力形式转变为摩阻力和桩端承载力的组合，与实验采用的加载方式有所不同。但由圣维南原理可知，在离加载位置较远的区域，实际荷载形式与实验采用均布荷载的形式对变形的影响是基本相同的，从研究边坡稳定的角度而言这种对荷载的简化是可以接受的。根据相似比关系计算得到的模型桥基荷载为0.26 kN 。

本次实验的采用逐级加载的方式进行加载，设计共加载12级，每级加载的大小为换算之后桥梁荷载。稳定后再施加下一级荷载。若施加过程中有明显水平变形趋势（水平位移 ≥ 1 mm），则停止加载，并按照3倍加载速率进行卸载。

2.2 数值计算方法简介

为了更好地研究边坡的变形破坏模式，建立与模型试验尺寸相同的有限元数值模型，并采用相同的材料参数以及加载过程模拟实验过程，来验证和扩展模型实验的结果。采用Phase2D软件建立的模型图如图5所示。模型采用三节点三角形单元进行划分，共计单元2 000個，节点1 310个。材料参数见表2。为了进一步研究内部不同区域的变形以及应力对荷载变化的响应情况，用与模型试验相同的方式加载至20倍桥基荷载，然后分析边坡对荷载的响应过程。

3 桥基荷载敏感性分区研究

在实际工程中，桥基荷载是通过由基础和地基组成的复杂结构传递到边坡内部，从而对边坡的稳定性产生影响。一般认为，桥基荷载作用的范围是有限的，且受坡体内部结构面或者软弱层位的影响较大。

3.1 基于位移增量的桥基荷载影响区域分析

当桥基荷载改变时，边坡体内部不同区域的变形也会产生不同的响应。这种响应可以用每一荷载等级下某点变形相对于前一级荷载产生变形的增量大小来衡量。当某点变形增量较大时，说明该点对于荷载的改变敏感，这些点的集合即为敏感区。若某点对于任一荷载改变变形增量均不大时，认为该点对荷载改变不敏感，其集合即为非敏感区。在这两个区域之间还存在过渡区域，当荷载增大时，这些过渡区域可能逐渐发展为敏感区域。本文提出变形影响系数作为标准进行划分，具体步骤如下：

1）按加载方案对模型施加荷载，求出边坡在不同荷载下的位移场。

2）在边坡位移场中选取一些横向的监测线（见图6），并沿这些监测线均匀提取位移数据。

3）求出各个监测点位移随荷载等级变化图（见图7a）、7b））。图中可以看出不同区域的位移曲线的弯曲程度差异很大，说明曲线的弯曲程度可以表征各点对荷载变化的敏感性。由于当曲线导数很小时，曲率与曲线的二阶导成正比关系。故求出位移曲线上各级数的二阶导数并取平均值，再对各平均值进行标准化处理，得到每条曲线的变形敏感性系数。通过这种处理，不同监测线上的位移的敏感程度就能在同一标准下进行比较。

4）将监测线各点的位移敏感性系数作图（见图8）。从各图中选出敏感区域及非敏感区域的取值范围，可以得到敏感区域下限值[δ1]和非敏感区域上限值[δ2]（见表3）。将[kij≥δ1]的部分划分为敏感点，将[kij≤δ2]的部分划分为非敏感点，其余部分为过渡点。

5）在监测线標出各点的敏感度，并据此得到边坡体内敏感区、过渡区及非敏感区的范围。

为了验证上述方法的合理性，根据模型试验中位于荷载下方监测点的位移数据进行同样的处理，最后与数值模拟结果相比较。从图8中可以看出，实测点和数值模拟得出的监测点位移敏感性系数非常吻合，说明这种方法能较好地反应边坡上某点对于荷载变化的响应情况。

3.2 软弱夹层模型位移敏感区域分析

根据上述方法就可以得到软弱夹层存在情况下边坡体内部水平位移及竖向位移的敏感区域的分布图（见图9）。从图中可以发现，边坡内部各点水平位移对于荷载变化的响应是不对称的。当荷载为5倍桥基荷载时，水平位移敏感区面积很小，主要集中在承台下方及前缘。随着荷载逐步增大（10倍桥基荷载），敏感区向两侧扩展，过渡区则往深部发育，但没有达到软弱夹层。当达到最终荷载时（60倍桥基荷载），在加载区域的后方，水平位移敏感区发展的深度和范围均有限，并很快过渡到非敏感区，说明承台处限制了水平位移的发展。而在靠近临空面的方向，敏感区范围则继续往深处发展，并向下一直延伸到软弱夹层，整体形状成鼓腹形。这说明，当荷载增大时，承台前缘的部分有向边坡体外部挤出的趋势。

竖向位移的响应与水平位移响应稍有不同。5倍桥基荷载时，边坡内部对荷载变化不敏感。过渡区则零星分布在承台两侧。当荷载增大到10倍桥基荷载后，承台下方敏感区的发展非常迅速，覆盖到下方的软弱夹层。过渡区的分布规律与敏感区基本一致。达到最终荷载后，竖向位移敏感区域向后缘发展。而软弱夹层以下的区域对荷载的敏感程度迅速降低，在深度上敏感区的扩展范围没有增加。

结合以上分析，可以得出桥基荷载的影响范围主要在边坡后缘到边坡中部，影响深度主要在软弱结构面以上。其中在承台处及后缘处，需要考虑竖向的沉降问题。在承台的前缘，则主要关注临空面向外挤出的位移问题。两个方向的位移敏感区域均在10倍桥梁荷载之后扩展到整个承台范围。这些区域的位移不仅在数值上很大，同时变化也非常剧烈，在工程上已经不可忽视。同时前后缘可能产生的变形形式及范围也不一致，需要对应采用不同的工程加固手段进行处理。

3.3 无软弱夹层模型位移敏感区域分析

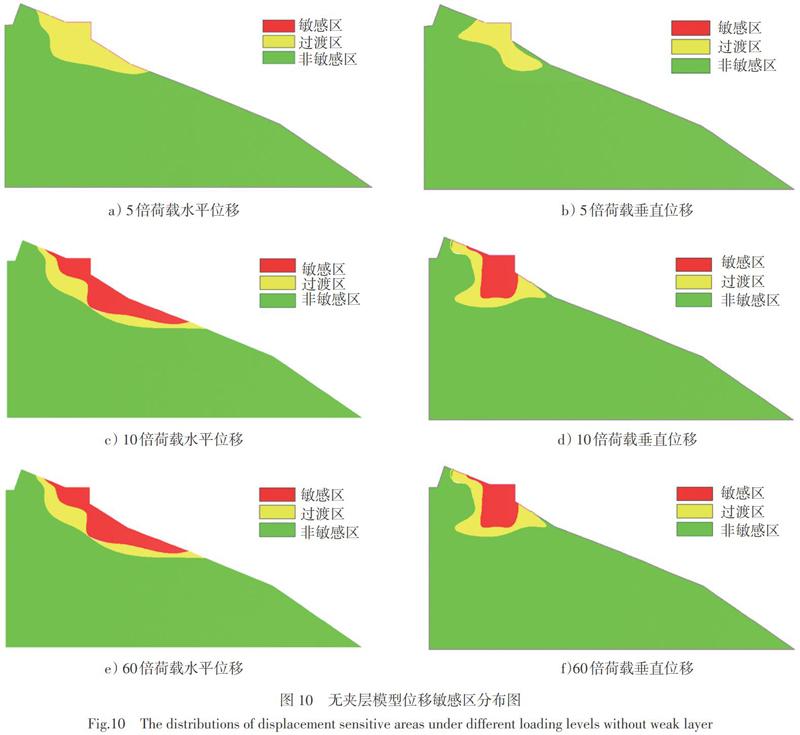
为了分析下伏软弱夹层的影响，在数值模型中去掉软弱层位，采用相同的方法，得到无夹层模型的竖向位移以及水平位移的敏感区分布图（如图10所示）。

当荷载较小时，水平位移对荷载的响应并不敏感，仅在承台处及承台前缘分布有过渡区。随着荷载的增大，过渡区逐渐发展为敏感区并向前沿继续扩大至3倍承台宽度处，此时可以认为在10倍桥基荷载下，承台局部向外挤出的趋势已经不可忽视。同时在边坡深部，也逐渐有过渡区形成。而在承台后缘，敏感区和过渡区的发展均有限。随着荷载继续增大，敏感区域的分布以及面积并没有明显变化。表明在10倍桥梁荷载之后，虽然位移在不断增加，敏感区域的发展已经趋于稳定。

与无软弱夹层模型进行对比可以发现，当荷载小于10倍设计荷载时，由于荷载影响范围还没有达到软弱夹层处，两种模型中敏感区域的分布类似。当位移继续增大后，无软弱夹层模型中敏感区不会随之继续发展。此时各点的位移虽然在不断增大，但其敏感性程度已不会继续发生改变。而当软弱夹层存在时，由于其强度较低，随着荷载的增加，沿着软弱夹层会发生较大的塑性变形。从而引导位移敏感区区域向下向深处持续发展，并形成鼓腹的形状。较大的桥梁荷载会逐步影响到边坡整体的稳定性问题。如果软弱夹层强度进一步降低，原来的过渡区或者非敏感区逐渐向敏感区域转变，并继续向下发展，最终从坡面剪出，形成一条完整的滑动面。无论是位移还是位移增量均会发生不可忽视的突变，预示着桥基边坡发生整体失稳。如果不进行必要的加固措施，可能会诱发更大的危害。

3.4 实际边坡模型位移分析

由于模型试验所代表的只是实际边坡中的一小部分区域，所以需要通过与实际边坡位移变化模式的比较来验证其准确性。在实际模型中，考虑了强风化岩层上覆的堆积体，关键层位仍为t2凝灰岩夹层。模型单元采用三角形六节点单元，共计单元数量1 982个，结点数量为3 982个。桥基荷载以均布荷载的形式作用于承台上，大小为867 kN/m2。实际模型中采用的材料参数见表4。

从结果中可以看出，与荷载较小时（5倍桥基荷载），水平位移整体量级较小，整个边坡位移没有出现明显分区，垂直位移仅在桥基下方局部区域较大。随着荷载逐渐增大，当达到14倍荷载时，在承台前后缘位移显著提高，分区现象显著;垂直位移显著增大，并且位移较大区域已拓展到软弱夹层处。当荷载达到60倍桥基荷载时，水平位移分区现象已经扩展到整个坡体，特别是在承台后缘处引起了较大的水平位移变形，而垂直位移的分布区域变化较小。与模型试验模型相比，实际模型的位移分布区域是十分类似的，均是随着荷载加大，位移较大的区域分别向前缘后缘发展，深度也逐渐加深，直至软弱夹层处。但是由于实际模型中堆积体以及强风化玄武岩层的变形参数相较模型试验中采用的玄武岩模拟材料要小，所以位移的扩展范围要比模型试验范围更大。总体来说，本文提出的位移敏感性分区方法能较好地确定边坡位移敏感区域，为工程建设提供良好的参考建议。

4 结语

本文基于室内边坡模型实验建立了有限元模型，采用位移敏感性系数的方法对边坡内部不同点对荷载响应程度进行分区研究，并与实际测量结果进行了比较，可以得到如下结论。

1）提出位移敏感性系数的概念，分析各点水平位移以及竖向位移对荷载变化的响应情况，将边坡体内部划分为位移敏感区、过渡区及非敏感区。通过与实际模型进行比较，认为该分区能较好地反应边坡内部位移对荷载的响应规律。

2）通过分析不同荷载等级下边坡内部位移敏感区的分布规律，认为在桥梁荷载作用下，承台前缘的部分有向边坡体外部挤出的趋势，在承台处以及在后缘处，需要考虑竖向的沉降问题。当桥梁荷载达到10倍设计桥梁荷载时，承台周围的位移变形已经不可忽视。