网格形变细分的大视差图像拼接算法

齐向明,王佳琦

(辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105)

0 概述

由于成像设备画幅和视角的限制,一次性拍摄全局图像一般不能满足实际需求,需要通过图像拼接技术对多幅具有重叠区域的数字图像进行匹配、配准和融合,以得到一幅大视角、高分辨率的拼接图像。在机器视觉、虚拟现实、测绘与遥感等领域,图像拼接已成为一项关键技术,引起了国内外相关学者的广泛关注。

图像拼接技术主要包括图像匹配、图像配准和图像融合三部分。图像匹配是图像配准的前提,其提取出2幅图像的特征。图像配准是图像拼接技术的核心,目的是利用重叠区域内的相同特征实现 2幅图像之间同一组特征的配准,图像配准算法直接影响图像拼接的精度。图像融合将变换到同一坐标系下的2幅图像进行重叠区域融合,性能良好的融合算法在一定程度上可以避免因配准算法较差造成的重叠区域重影问题。

本文总结图像拼接技术的研究现状,对图像配准算法进行研究,归纳传统图像配准算法中存在的不足,在此基础上,提出一种网格形变细分的大视差图像拼接算法,以提高图像配准精度。

1 相关工作

文献[1]提出一种基于局部不变的图像拼接方法,其先通过尺度不变特征变换(Scale Invariant Feature Transform,SIFT)算法匹配图像,再利用随机采样一致性算法选择内点,最后计算出单应矩阵以完成 2幅图像的拼接。该方法对拼接图像的要求较高,若2幅图像具有视差,会出现严重的鬼影现象。针对文献[1]方法的不足,文献[2]将待拼接图像分为前景和后景,分别建立2个单应矩阵来拼接2幅图像。该方式在一定程度上解决了文献[1]中的问题,但当图像重叠部分差别较大时,仍会出现鬼影问题。文献[3]提出了一种平滑仿射变换算法,其建立多个单应矩阵来拼接图像,该算法具有很好的局部适应能力,但对纹理复杂的图像进行拼接时依然会出现重影现象。

文献[4]提出一种建立网格形变的方法,首先建立Moving DLT(Moving Direct Linear Transformation)数学模型,然后解超定方程生成网格单应矩阵并对每个网格进行透视变换。网格单应矩阵有效地防止了重影的产生,但未限定网格的数量和大小,也未处理非重叠区域的透视失真问题。文献[5]提出基于保形差值的方法,将重叠区域的投影变换逐渐过渡到非重叠区域的相似变换,其可以有效校正图像非重叠区域的透视失真问题,但对于视差较大的图像,需要结合文献[4]中的算法进行处理。文献[6]提出一种尽可能自然投影算法(Adaptive As-Natural-As-Possible,AANAP),其将局部变换与全局变换相结合,不仅有效消除了重叠区域的鬼影现象,还可以使拼接图像更加美观,但该算法需要对待拼接的2幅图像同时进行网格形变,导致消耗时间较长。文献[7]提出L-mDLT(Line moving Direct Linear Transformation)算法,其主要针对城市建筑等有规律的形状物体图像进行拼接,通过成对特征点与成对特征线相结合来判断拼接图像的误差,但该算法针对性较强,应用范围较小。

文献[8]提出NISwGSP(Natural Image Stitching with the Global Similarity Prior)算法,其使用尽可能投影算法(As-Projective-As-Possible Image Stitching,APAP)[4]初始化局部变换矩阵,用约束项同时作用在局部适应变换和全局适应变换,从而有效降低全局拼接误差,但该算法关注于校正非重叠区域的透视失真,重叠区配准精度较差。文献[9]在NISwGSP算法的基础上,提出MISwLP(Mesh-based Image Stitching with Linear Structure Protection)算法,该算法通过提取图像中的直线结构并施加约束,达到了保护原图像中直线结构的目的,相较NISwGSP算法有效削弱了透视失真,但其仍未提升重叠区域的配准精度。文献[10]利用差异图像计算权重并扩展和细分重叠区域,从而改进最佳缝合线,该算法从拼接缝合线角度考虑,对视差较小的拼接图像效果较好,但对大视差图像会出现严重的拼接错位。文献[11]提出基于显性子平面自动配准的拼接方法,其利用拼接误差与聚类算法确定局部适应矩阵的位置,使用局部投影实现拼接,该方法使用APAP算法实现局部变换调整,可以在重叠区域有效防止鬼影现象,但其未处理非重叠区域拼接后发生的透视失真问题,引入聚类算法后导致拼接速度较慢。文献[12]提出基于线约束的全局相似性约束拼接模型,首先利用匹配的点和线特征计算图像的翘曲,然后借助APAP算法进一步配准图像,并利用点线结构和全局相似变换矩阵作为图像形变的约束项。该模型对纹理简单且线条丰富的图像拼接效果较好,但未进一步优化APAP算法,纹理复杂的图像在拼接时会产生较大的误差。

以上算法针对2幅大视差图像拼接时出现的不同程度的重叠区域重影、非重叠区域透视失真等问题进行了深入的研究和探索,但仍然存在以下不足:未说明APAP算法中网格单应矩阵的密度,造成图像配准精度下降,致使图像拼接的重叠区域出现严重重影;在图像配准时,非重叠区域会因网格单应矩阵变换造成透视失真,导致拼接图像与实际画面差别较大;对于重叠区域纹理复杂度较高的区域,仅依靠APAP算法难以对像素进行配准,致使图像清晰度下降。

针对上述问题,本文提出一种网格形变细分的大视差图像拼接算法。在利用APAP算法建立低密度网格形变的基础上,按照成对匹配点对重叠区域内的网格形变进行细分。使用随机采样一致性算法计算全局最优相似矩阵,校正非重叠区域发生的透视失真现象。通过全局最优相似矩阵与网格单应矩阵的加权叠加,实现目标图像形变。在此基础上,利用内容感知算法寻找目标图像重叠区域中重要度较低的部分,与待拼接图像加权融合从而完成拼接。

2 算法原理

2.1 APAP算法及网格形变细分

通过APAP算法对大视差目标图像进行网格划分,每一个网格代表一个单应变换矩阵,利用局部调整的方式将2幅具有大视差的图像进行配准。设图像I和I′是一组待拼接图像,它们对应的匹配点为p=[x,y,1]T、p′=[x′,y′,1],则对应的变换关系为p′=h(p),横纵坐标关系如式(1)和式(2)所示。

(1)

(2)

齐次坐标p=[x,y,1]T和p′=[x′,y′,1]对应的变换关系为式(3)。

p′～Hp

(3)

(4)

将式(4)转化为Ah=0,如式(5)所示。

(5)

对于图像I和I′,共有N组对应的匹配点,则DLT算法自适应矩阵h可表示为:

(6)

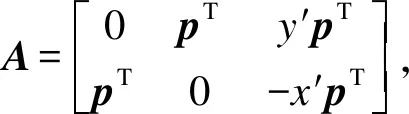
文献[4]提出了Moving DLT算法模型,对式(6)添加权值估计网格自适应矩阵,则网格pj的自适应矩阵表示为:

(7)

其中,j为网格的数量,j=C1×C2,C1和C2为横纵网格数,Wj=diag([ω1,j,ω1,j,…,ωN,j,ωN,j]),ω1,j=exp(-‖p-pj‖2/σ2),σ为高斯函数尺度因子,pj为网格内的特征点。

本文使用SIFT算法[12]生成成对特征点,根据SIFT算法的原理可知,特征点数量分布与图像纹理的复杂度相关。若将图像分为C1×C2个网格,利用Moving DLT算法计算每个网格的单应矩阵Hn,1,n∈{1,2,…,C1×C2}。但是,网格的密度过于稀疏,对于目标图像纹理复杂的重叠区域,很容易出现重影现象。

在重叠区域,网格n中的特征点数量为m,如果m≥η,则对网格n进行二次细分,其中,η为需要二次细分网格的最少成对匹配点数。二次细分c1×c2个网格,利用Moving DLT算法计算二次网格形变的单应矩阵Hn,m,n∈{1,2,…,C1×C2},m∈{1,2,…,c1×c2}。

2.2 全局最优相似变换

成像设备在不同平面拍摄时2张图像之间的夹角将不同,根据成对特征点的分布,由不同簇特征点可以计算出不同夹角,角度最小的仿射变换矩阵即为全局最优相似变换矩阵。通过全局最优相似变换可以有效降低非重叠区域的透视失真现象。计算全局最优相似变换矩阵的具体步骤如下:

输入图像成对匹配点

输出全局最优相似变换矩阵

步骤1使用随机采样一致性算法[13]去除错误匹配,成对特征点投影矩阵误差的阈值为εg,以此保留最佳匹配点。

步骤2While(i--)

在获得最佳匹配点后,再使用随机采样一致性算法选择内点Pi={p1,p2,…,pn},误差阈值为εl且满足εg>εl。则Pi对应的仿射矩阵为:

(8)

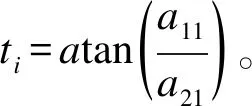
Ifn<λ,λ为预设的最少匹配点数

退出循环;

End

选择最小变换角度t对应的仿射变换矩阵S作为全局最优相似变换矩阵。

2.3 内容感知

内容感知算法[14]可以自动识别图像的内容重要性[15],其主要应用于图像缩放和剪贴,旨在保留重要度较高的区域。通过计算能量函数,可以寻找其值积累最小的像素线。具体步骤如下:

步骤1灰度化图像O,利用sobel算子计算O区域的能量图像e。

步骤2计算灰度图像O每个像素点的累计能量M,计算公式如式(9)所示。

M(i,j)=e(i,j)+min(M(i-1,j-1),

M(i,j-1),M(i+1,j-1))

(9)

步骤3计算灰度图像O在竖直方向的能量函数值积累最小像素线S,S定义如式(10)所示。

(10)

其中,m为重叠区域O竖直方向的像素数。

3 算法实现

3.1 网格形变细分

利用SIFT算法[16]对待拼接图像进行特征点检测和匹配,再根据随机采样一致性算法选择最优内点,随机采样一致性算法阈值εg=0.1。根据2.1节中APAP算法构建粗网格形变单应矩阵,对目标图像进行Moving DLT变换,网格形变数量为C1×C2=10×10。

根据SIFT算法的成对特征点分布,对APAP算法的粗网格形变进行细分,单个网格内特征点的阈值为η,η=10,细网格形变数量为c1=c2=2。网格形变细分结果如图1所示。

图1 网格形变细分结果

3.2 非重叠区域校正

使用2.2节中的随机采样一致性算法,选择不同簇的成对特征点,计算全局最优相似变换矩阵。在选择不同簇时,局部随机采样一致性算法的阈值为εl=0.001,计算出全局最优相似变换矩阵S,用以调整目标图像的透视失真现象,从而避免非重叠区域的透视失真问题。

3.3 形变矩阵叠加

2.1节和2.2节分别计算网格单应矩阵Hn,m和全局最优相似变换矩阵S,在本节中对2个矩阵加权叠加,计算出目标图像的形变矩阵,如下:

(11)

其中,Hn,m是第n个粗网格中第m个细网格单应矩阵,μn,m和μ′n,m为权值系数,且满足μn,m+μ′n,m=1。μn,m可通过式(12)计算。

(12)

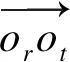
3.4 重叠区域的感知与拼接

通过前文已对目标图像进行配准和校正,本节将完成目标图像的感知和融合。借助2.3节的算法,内容感知待拼接图像重叠区域,保留重要度较低区域并进行配准。目标图像的重叠区域O以竖直方向的能量函数值积累最小的像素线S为界,截取重要度较低区域图像进行融合。

为防止拼接图像出现视觉不适,对重叠部分加权融合[17],如下:

(13)

其中,w1、w2表示加权的权重系数,且w1+w2=1。

4 实验结果与分析

本文以Matlab R2014a作为实验平台,使用文献[4]数据集中的3组图像,名称(大小)分别为:Rail Tracks(600×800×3),Temple(487×730×3),Garden(1 000×750×3)。使用上述3组图像分别对APAP算法、SPHP算法、AANAP算法和本文算法作对比实验,主要从视觉主观[18]、量化对齐和拼接速度等方面验证算法的性能优劣。

4.1 主要参数分析

本文可调节的主要参数可以分为两大类。第一类为网格优化参数,包括稀疏网格数量C1×C2、单个稀疏网格内特征点阈值η和稀疏网格内的细网格数量c1×c2。第二类为随机参数一致性阈值εg和εl。

稀疏网格的数量直接影响图像重叠区域的配准精度,网格数量过多会造成配准速度下降。如图2所示,以Temple组图像为例,横坐标为图像形变网格的C1值,且C1=C2,由图2可得,随着网格数量的增加,配准时间急剧增加,本文选择的测试图像尺寸较小,而且会对稀疏网格进行进一步细分,因此选择C1=C2=10。由SIFT算法的原理可知,特征点密度越高则表示该区域的纹理复杂度越高,由2.1节可知网格的单应矩阵计算至少需要4组成对匹配点,因此,阈值η小于4时并不会使图像的配准精度增加,反而会使配准速度下降,阈值过大会造成配准精度下降和配准速度增加,因此,在本文中η取值为10。特征点数量决定了细分网格的数量,c1和c2值过小会造成配准速度下降,过大会造成配准精度下降,由于本文选择图像的尺寸较小,单个稀疏网格内特征点数量较少,因此c1和c2值为2。

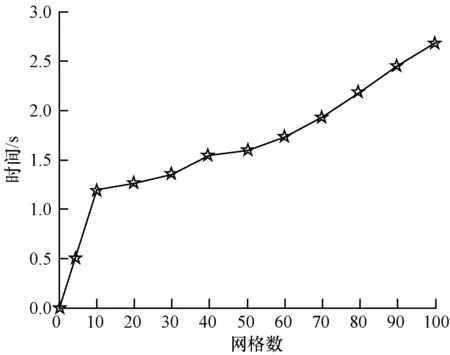
图2 不同网格数下的拼接时间

随机参数一致性阈值εg是一个经验值,εg过大可以增加成对匹配点的数量,有助于图像重叠区域的配准,但内点中错误匹配点的数量会增加,造成配准失败,经过多次测试,εg=0.1最佳。随机参数一致性阈值εl也是一个经验值,经过多次实验,当εl=0.001时所分出的特征点簇最佳。

4.2 视觉主观评价

图3所示为APAP、AANAP、SPHP的拼接结果和本文算法在文献[4]数据集中的Rail Tracks图像上的拼接结果。其中,实线区域为拼接图像重叠区域的误差,虚线区域为非重叠区域发生的透视失真范围。在图3(a)中,APAP算法使用局部网格来调整图像,重叠区域配准效果较理想,但非重叠区域没有透视失真校正,发生了严重畸变,其中,树木发生了严重的倾斜,与真实图像差别较大。在图3(b)中,AANAP算法先使用APAP算法进行局部配准,再调整部分非重叠区域,最后调整全局拼接图像。该算法对重叠区域配准效果良好,但非重叠区域会发生透视失真,且会造成拼接接口位差,如图3(b)中的树木和塔吊拼接线位置。SPHP算法更注重非重叠区域透视变换和减少失真,但重叠区域拼接精度却很差,如图3(c)中非重叠区域没有发生明显形变,但重叠区域出现了严重重影。图3(d)为本文算法拼接结果,该算法根据匹配点的分布对网格细分,寻找目标变换图像的全局最优相似变换,将全局最优相似变换矩阵和网格单应矩阵加权叠加,不仅可以精密调整重叠区域,而且使得非重叠区域透视失真最小,最后再对重叠区域的内容进行感知,保留重要度较低的区域并融合拼接,使拼接效果更能还原真实场景。

图3 4种算法拼接结果比较

使用国际无线电咨询委员会制订的CCIR500-1图像拼接效果主观评价标准[19],对APAP算法、SPHP算法、AANAP算法和本文算法的拼接效果进行比较,结果如表1所示。从表1可以看出,本文算法得到的拼接图像均为5级,拼接效果最好。

表1 不同算法拼接效果主观评价结果

Table 1 Subjective evaluation results of splicing effect of different algorithms

图像APAP算法SPHP算法AANAP算法本文算法Temple5455Garden5345Rail Tracks4345

4.3 量化对齐评价

本文计算重叠区域对应拼接像素点的均方根误差(RMSE)[20],以判定拼接质量。RMSE计算公式如式(14)所示。

(14)

其中,M、N为重叠区域O的尺寸,IO(i,j)、I′O(i,j)分别是拼接图像的相互重叠部分。APAP算法、SPHP算法、AANAP算法和本文算法拼接图像的RMSE值如表2所示。

表2 不同算法的RMSE值

由于不同待拼接图像的视差大小和纹理复杂度不同,因此拼接后的RMSE值有所不同。SPHP算法主要调整非重叠区域的透视失真,由于网格细分较为稀疏,因此对视差较大和重叠区域纹理较为复杂的图像拼接质量较差,RMSE值最大。AANAP算法同时调整2幅待拼接图像,但为了改善非重叠区域的透视失真,对重叠区域调整不足导致重叠区域的RMSE值高于APAP算法。APAP算法中单应矩阵数量固定,不能根据图像的纹理特征自主优化单应矩阵数量,对于纹理较为复杂的区域,固定的投影矩阵不足以进行精密调整。本文算法根据重叠区域的纹理复杂度精密细分网格稀疏程度,又对待拼接图像的重叠区域进行内容感知,保留重要度较低的区域实现图像拼接,故其RMSE值最小。

4.4 算法效率对比

将APAP、SPHP、AANAP和本文算法的拼接速度进行对比,所有代码均在Matlab 2014上运行,APAP算法的网格数量默认为100×100。各算法的拼接时间对比结果如表3所示。

表3 不同算法的拼接时间

APAP算法仅对一张图像进行形变,未考虑图像纹理特征对网格细分的影响,故拼接速度最快。SPHP算法不仅需要对待拼接图像进行网格形变,还需调整非重叠区域的透视失真,故拼接速度不及APAP算法。本文算法细分网格形变对重叠区域进行拼接,在一定程度上加速了APAP拼接算法,但为了减小非重叠区域透视失真和保留最清晰的重叠区域,从而降低了拼接速度。AANAP算法不仅需要计算2张待拼接图像的网格形变局部矩阵,同时还需要使用随机采样一致性算法优化最优相似变换矩阵,故计算数据最多,拼接速度最慢。

5 结束语

本文提出一种网格形变细分的大视差图像拼接算法,根据成对匹配点的分布对网格形变进行细分,达到对重叠区域精确配准的目的。利用随机采样一致性算法选择全局最优相似变换矩阵,将网格单应矩阵和全局最优变换矩阵加权叠加,以避免非重叠区域的透视失真问题。在此基础上,对重叠区域进行内容感知,保留重要度较低的区域并完成拼接,以提高拼接图像重叠部分的清晰度。实验结果表明,该算法对大视差图像进行拼接时,能够在重叠区域有效削弱重影现象,在非重叠区域改善透视失真问题,且拼接结果能够还原真实场景。在实际应用中,拼接图像特征点分布不均匀或者数量较少时,选择特征点时将有一定难度,下一步将对此情境下的特征点选择方式进行研究。