灰岩冻融循环的劣化规律研究

刘 晨， 于清杨， 王城斌， 宋泽宇， 杜博宇

(1.吉林大学 建设工程学院，吉林 长春 130026； 2.吉林省长春生态环境监测中心，吉林 长春 130022)

我国东北地区分布着大量的季节性冻土区域，修建在季冻区的公路、铁路隧道、桥梁等重要基础设施在运营期间由于季节更替、昼夜循环，遭受着围岩冻胀的影响导致冻融破坏，影响着隧道的安全运营。造成围岩冻融破坏的主要原因是岩体内的液态水随温度变化冻结成固态冰，相变过程中岩体内部微观结构和宏观结构的变化导致围岩内部劣化。

目前国内外学者对岩石冻融循环后的物理力学特性及损伤劣化方面开展了一定的研究，如徐光苗等[1-2]在-20～20 ℃以及干燥和饱水环境下对岩样进行单轴及三轴试验，分析了不同受力环境下岩石的破坏规律，给出了波速、导热系数与温度之间的关系，提出了分别代表砂岩和灰岩的冻融损伤模型；Yavuz等[3]对安山岩进行20次冻融循环及热冲击后发现岩样P波波速及施密特硬度降低，并对试验数据进行多元回归分析，建立了预测冻融循环后岩石参数的模型。Momeni. A等[4]在300次冻融循环后探究其对伊朗Alvand硬岩物理力学性质的影响。贾海梁等[5]利用不同周期的疲劳荷载模拟自然条件下的冻融循环，且周期应用顺序对损伤结果影响较大。唐江涛等[6]利用3种岩石进行冻融循环，利用X射线光粉晶衍射试验等发现岩石内部矿物质成分的转化以及波速、质量和含水率等变化。Ghobadi等[7]利用伊朗砂岩进行冻融循环，分析其物理力学损失，并使用衰变函数模型统计崩解速率。张慧梅等[8]从细观力学及宏观唯象角度出发探讨了冻融受荷岩石损伤模型。龙翔等[9]利用循环冻融研究油页岩内部裂隙损伤进而探究其热传效率。赵尚传等[10]通过对混凝土的冻融耐久性进行测评研究其破坏机理。 Al-Omari A等[11]利用灰岩在热应力、冷凝及冻融3种环境下研究了多孔结构内部损伤规律以及岩石表面剥落因素的影响。Zhong Zhou等[12]利用土-岩混合物进行冻融循环，并通过PFC3D实现混合物的细观模拟。Weng Fang等[13]通过引入冷却衰减模型探索应力应变特征参数解析表达。Dengxing Qu等[14]引入损伤修正系数酸性冻融下岩样损伤进行调整并建立相应本构方程。可以看出，目前国内外学者在岩石冻融损伤方面的研究不断进行，对损伤机理、物理力学性质和损伤影响条件等方面有所进展，但围岩冻融损伤复杂性高，针对不同研究区域影响条件更复杂，尤其是季冻区的围岩冻融循环的研究还远远不够。

本文基于现有的岩石损伤模型，建立针对吉林省季冻区后崴子隧道的冻岩损伤模型。通过对灰岩的冻融循环试验等物理力学实验，得到研究区域内灰岩的冻融劣化规律。

1 灰岩冻融损伤模型

Lemaitre提出的应变等价理论中指出[15]：在应变本构方程中任意损伤引起的通常应力可以无损材料中的有效应力代替，即：

ε=σ/E′=σ′/E

(1)

式中：E、E′——分别为无、有损材料的弹性模量。

因多数岩石具有初始破坏，实际的完整围岩弹性模量较难获得。张全胜等[16]提出推广后的应变等价理论可知：

σ1A1=σ2A2

(2)

式中：σ1、σ2、A1、A2——分别为岩石损伤后产生的两种损伤状态下的有效应力和面积。

则可推出其应变为：

ε=σ1/E2=σ2/E1

(3)

式中：E1、E2——分别为岩石材料受力损伤后两种损伤状态下的弹性模量。

同样基于该原理，将围岩的初始损伤及冻融后的损伤分别定义为两种损伤状态。则

σ0A0=σnAn

(4)

Dn=(A0-An)/A0

(5)

式中：Dn——n次冻融循环下的冻融损伤变量。

联立式(4)、(5)可得：

σn=σ0/(1-Dn)

(6)

则两种状态下的应变为：

ε=σ0/En=σn/E0

(7)

联立式(6)、(7)可得这两种损伤的本构关系分别为：

En=E0(1-Dn)

(8)

σn=E0(1-Dn)εn

(9)

再次应用上述推导理论分别定义冻融、受荷损伤为两种损伤状态，可得岩样共同损伤下总的应力应变关系为：

σm=εmEn/(1-Dp)

(10)

式中：Dp——受荷损伤变量；σm、εm——m次冻融循环后的有效应力和应变。

由式(8)、(10)可得冻融受荷后的总损伤应力应变关系为：

σm=εmE0/(1-Dm)

(11)

其中：

Dm=Dn+Dp-DnDp

(12)

式中：Dm——冻融受荷下岩石材料的损伤变量。

式(12)表明冻融与荷载两种作用对岩石材料的耦合劣化作用。

在这两种作用下，岩石材料结构发生微小变化，其宏观的性质变化可反映出内部微观的破坏程度。由式(8)可将岩石冻融损伤变量表示为：

Dn=1-En/E0

(13)

岩石内部微观结构并不均匀，其劣化程度主要与单元体内的缺陷有关，因单元体的强度受其影响，因此Dp与单元体损伤的应变存在如下关系：

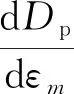
(14)

式中：φ(ε)——岩石材料在受荷过程中单元体的损伤率，反映了岩石的损伤程度，但依据杨天鸿等[17]的理论，微观上的单元体没有损伤率，只有破坏与否。岩石材料宏观强度的损伤即单元体的破坏的累积。

通过宁建国等[18]的双参数的Weibull分布理论，由式(14)可得到受荷岩石的损伤方程为：

(15)

式中：m——岩石材料损伤特征参数，m=1/ln(εfE0/σf)；εf——应变峰值。

代入式(12)、(13)可得到总损伤方程为：

(16)

由式(16)可知，总损伤变量Dm与冻融后的弹性模量、初始模量、岩石材料损伤特征参数、应变以及应变峰值有关，冻融后的弹性模量受冻融次数的影响。

2 灰岩冻融损伤的试验研究

2.1 试验设备

本次试验使用MDF-40H105型冻融箱，其温度范围为-10～-40 ℃；波速测试使用RSM-SY6型声波检测仪。

2.2 试验步骤

为尽可能模拟灰岩赋存条件，本次设计试验步骤如下[19-20]：

(1)灰岩试件制作。选取后崴子隧道典型灰岩岩样，按照试验要求标准制作成灰岩试件15个，3个一组。

(2)将试件放置105 ℃的烘箱中烘干至恒重，冷却后测量所有试件的质量以及纵波波速。

(3)对所有试件进行强制真空饱水，测量饱和后试件的纵波波速、质量。

(4)将所有试件用保鲜膜包裹后放置于冰箱内进行冻融循环试验，并控制冻融温度为-20 ℃左右，4 h后取出置于常温下融化4 h，一个冻融周期为8 h。

(5)在冻融0、2、5、10、20、30、40次时，取样测量其质量，并对试样进行纵波波速试验。

(6)冻融后对5组试样分别进行单轴抗压强度试验，观察外观。

2.3 试验结果及分析

2.3.1 外观损伤

冻融循环后不同结构、成分和强度的岩石表面可能出现不同的岩样破坏，对应于表面颗粒之间连接较弱，表面有大量自由颗粒且孔隙率大的岩石会出现颗粒损失模式；矿物成分简单，孔隙率小，强度较高的岩石会出现片落现象；结构较致密，强度相对较高的层理岩体，出现裂纹[21-23]。

本次试验通过对冻融循环过程中的岩样外观变化的观察，灰岩的表面变化较少，在冻融循环30～40次的时候，岩样表面出现了一部分片落现象(见图1)。这是由于灰岩矿物成分单一，孔隙率小且强度比较高。经过40次冻融循环的情况下，灰岩岩样产生的损伤劣化对整个岩样的岩体结构影响较小。

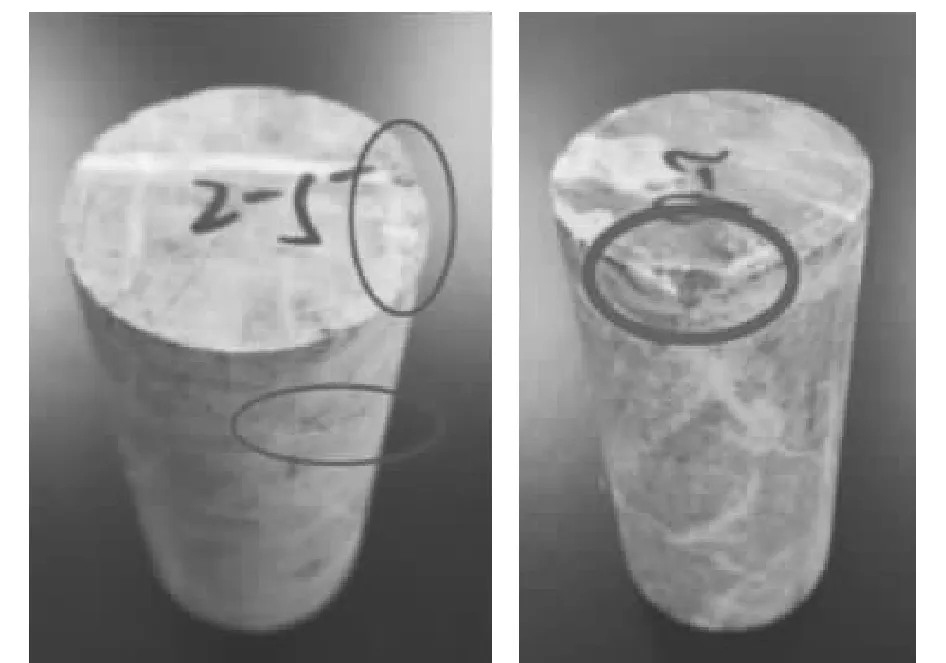
图1 冻融40次后的岩样外观

2.3.2 质量变化

本次试验使用的天平精度为0.01 g，获得岩样质量分布范围为500～520 g。冻融后即称量，不补充水分故不考虑水循环，由于材料之间的质量差较大，因此以质量变化量来说明。

由图2、图3中可看出，整体上随着冻融循环次数的增加灰岩的质量先上升后下降。在冻融循环期间，质量变化率最大损失为0.074%，最大增量为0.242%。冻融循环早期的质量升高主要是由于岩石材料表层的微裂隙中的水结冰引起的冻胀力作用造成一部分表层的微孔隙发育，这样的扩展有利于水分渗透到岩石中。

经过5～20次的冻融循环后，灰岩的质量有明显的下降，这是由于冻融循环导致岩石损伤加剧，微孔隙进一步发育，水分不断转移，同时岩样表面的自由颗粒増多，水分转移消除了部分损失的质量。因此，在一定次数的冻融循环后，岩石经过较长时间的风化作用，自身的状态较不稳定，如此前期的变化和破坏在冻融循环的劣化作用趋势明显。但经过多次的冻融循环，岩样发生劣化后会达到新的较稳定状态，随着岩石对冻胀力的平均抗拉强度增加，质量损失率相应减小。

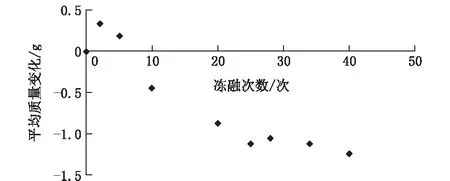
图2 冻融次数对平均质量的影响

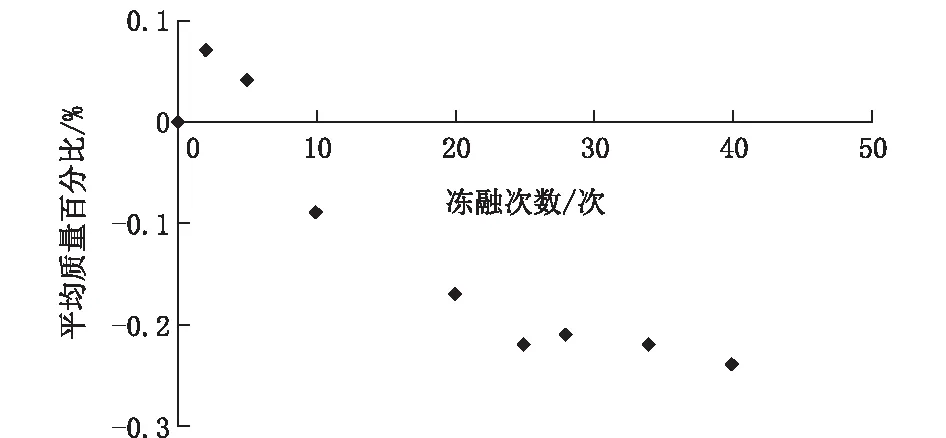
图3 冻融次数对平均质量百分比的影响

2.3.3 纵波波速试验

波速的大小反映了围岩的致密程度，从本质上来说，波速的大小与岩石内部的孔隙、裂隙密切相关。冻融循环试验的岩石样品的劣化程度可以通过波速的变化间接地反映出来。从图4可以得出结论，试验进行中，岩样的纵波波速先增加，随后缓慢下降，这是因为前期的冻融循环使微空隙不断扩展贯通，其中又有水分逐渐填充空隙，波速上升；而在后期岩石完整性下降，波速降低。冻融40次后，材料波速损失为36.63%。

图4 冻融次数对平均纵波波速的影响

2.3.4 单轴抗压强度试验

由图5、图6可明显看出，岩样试件加载前期经过了裂隙闭合阶段，其间岩样内部的微空隙随着外力的增加而逐渐压密，这一阶段并不明显，切线斜率较大，主要由于原生裂隙较少；弹性变形阶段随着外力的增加表现出线性变化的特点。同时可看出，后期的破坏阶段随损伤加剧斜率变缓，并且随着冻融损伤程度变大，裂隙闭合阶段变长。30～40次的峰值应力由于误差数据不明显。

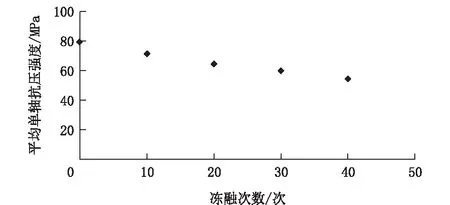
图5 冻融次数对平均单轴抗压强度的影响

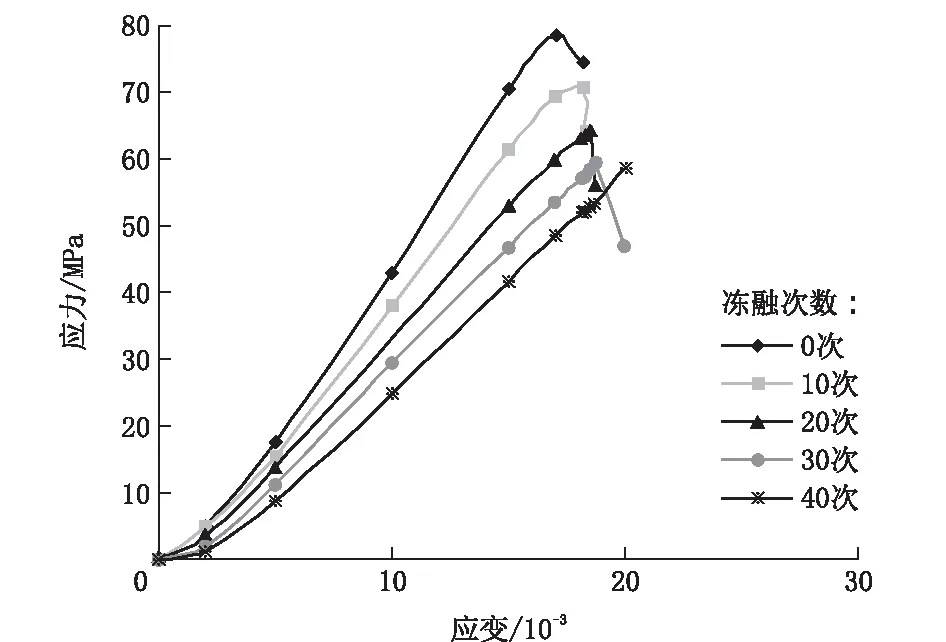
图6 不同冻融次数的应力应变关系

3 灰岩的冻融损伤分析

根据前面得到的后崴子隧道灰岩单轴抗压强度试验实测值，利用式(16)来计算灰岩材料的冻融受荷总损伤变量Dm的演化曲线。首先需计算出岩石材料损伤特征参数m，取值公式即m=1/ln(εfE0/σf)。参数见表1。

表1 后崴子隧道灰岩岩石材料参数

通过表1参数计算出后崴子隧道灰岩总损伤变量Dm与应变ε之间的关系见图7。

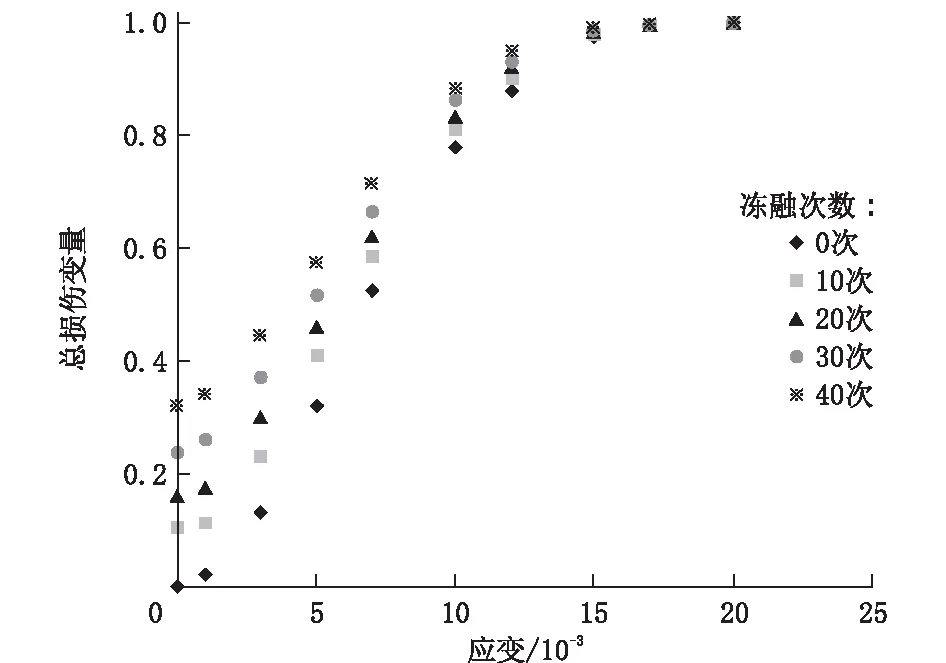
图7 后崴子隧道灰岩总损伤变量与应变的关系

从图7中可以看出，同一冻融循环次数下，后崴子隧道灰岩总损伤变量随其应变的增大而增大。同一应变条件下灰岩的损伤变量与冻融次数呈正相关，相同损伤程度时，冻融次数与岩石应变量为负相关；在应变为0时，未经冻融循环的岩石无损伤变量，而经历多次循环后，灰岩的冻融损伤变量分别为0.102、0.159、0.238、0.319。由图7可知未冻融灰岩在初始阶段即裂隙闭合阶段曲线较缓，推断内部孔隙裂隙少，岩样较为致密；随后的冻融循环加深了岩石材料孔隙裂隙的损伤率，使得初期裂隙闭合阶段曲线变陡，并且在每次冻融之后，由于冰的冻胀，裂缝增加并且水迁移导致岩石内的微孔隙裂隙增加。在岩石继续变形至破坏的过程中，岩石内微裂缝发育至汇合贯通，直至总损伤变量趋于1，最终达到峰值破坏。但在较大应变情况下，无论循环次数为多少，其损伤变量及应变都逐渐趋近，此时其损伤变量趋近1，说明在应变达到一定程度时，二者的耦合可适当缓解岩石的破坏，且表明冻融循环次数不是影响强度极限的主要因素，灰岩最终破坏。

4 结论

(1)基于岩石损伤模型，推导建立了后崴子隧道灰岩内部细观层次上冻融-荷载耦合破坏机制模型。

(2)测试了后崴子隧道灰岩岩样不同循环次数后的物理力学特征，分析发现：在冻融循环作用下，灰岩呈现出片落模式的冻融劣化，岩样的质量、纵波波速先增后减，单轴抗压强度持续减小，弹性模量和峰值应变则随冻融次数逐渐增大。

(3)分析了冻融循环作用下后崴子隧道灰岩总损伤变量与应变的关系，冻融和载荷的共同作用会使总损伤加剧，但损伤曲线表明耦合作用也可适当缓解这一影响，同时灰岩应变值趋于一致表明冻融循环次数并非影响其强度极限的主要因素。

(4)对岩石工程性质的研究主要基于室内试验，不能较好的模拟围岩岩体的周边环境，如果可以进行实地的原型比例模拟实验的话，将对围岩岩体的损伤研究和冻融循环过程有更直观更准确的研究结果。因此针对季冻区冻融围岩的研究还有很大的发展前景。