Heston模型下DC型养老金等价管理费用问题研究

李方超，张成科，朱怀念

(1.广东工业大学管理学院，广东 广州 510520；2.广东工业大学经济与贸易学院，广东 广州 510520)

1 引言

养老金计划是一项关乎国民生计的政策问题，是大多数国家养老保险制度中最主要的组成部分。随着世界人口结构不断趋于老龄化，养老保障压力也随之愈大，各国政府将不断加大养老金计划在其财政支出中的比重，各金融机构的养老金结余也日益增长。据我国人力资源和社会保障部的统计数据显示，2017年企业养老保险基金收入3.27万亿元，支出2.86万亿元，比2016年支出增长10.4%，当期结余4187亿元，累计结余达4.12万亿元。面对规模如此庞大的养老金，如何对其进行资产配置以实现保值增值，对于养老金管理者来说显得格外重要。

养老金计划主要可以设计为DB(待遇确定)型和DC(缴费确定)型两种。在DB型养老金模式下，参保人在退休后每月领取的养老金数量是固定的，这类计划收入稳定，参保人不需要考虑市场风险。在DC型养老金模式下，参保人建立个人养老金账户，每月按固定的缴费率缴纳费用，到退休时向养老基金缴纳的保费是确定的，退休后可以按月从养老金账户中领取养老金，由于养老金的总额包括缴纳费用和投资收益，其每月领取的养老金是不确定的，参保人需自行承担投资风险，这类计划是当前最主流的养老金模式。

近年来，越来越多的学者对DC型养老金的投资管理进行了细致的研究。有关DC型养老金最优投资管理的研究主要是围绕两个最优化问题展开：一是期末财富效用最大化，二是投资风险最小化。第一类优化目标注重养老金投资收益，以实现期末更高养老效用。Gao Jianwei[1-2]在CRRA效用与CARA效用下，以最大化终端时刻财富的期望效用为目标，研究了DC型企业年金在退休前与退休后的最优投资策略的CEV模型，得出了显式解。Guan Guohui和Liang Zongxia[3]在随机利率和随机波动率框架下研究了DC型养老金计划的最优投资问题，以期最大化养老金终端财富的期望CRRA效用，通过随机规划方法得到问题的解析解，并以数值方法来探讨金融参数对最优策略的影响。而第二类优化目标关注点在于养老金投资风险性，在有稳定投资收益的同时尽量降低风险。Ngwira和Gerrard[4]建立了两个实际与预期中枢二次偏差效用函数，以最小化实际给付与预期给付中枢的二次偏差和最小化实际账户余额与余额中枢的二次偏差作为优化目标，研究了养老金最优投资与给付问题。何林[5]将生存者利益部分的保险精算规律引入DC型企业年金账户余额的动态变化过程中，以实际给付额与预期给付中枢的二次偏差最小化作为优化目标，通过HJB变分法与随机控制理论，求得了最优资产配置比例与最优给付方案的解析解。考虑到优化目标的全面性，有学者指出单以期末财富期望效用最大化或投资风险最小化为优化目标求得的最优策略是短视的，均值—方差模型考虑终端财富期望效用最大化和终端财富方差最小化为目标，有效的克服了单目标效用函数的缺陷。Li Danping等[6]在CEV模型下，考虑违约风险和保费退还，以均值—方差为优化目标，得到了养老金的均衡投资策略。Menoncin和Vigna[7]在固定缴费养老金计划的积累阶段，考虑随机利率，通过解决一个均值—方差优化问题，提供了有效前沿的一般形式和最优投资策略。与此同时，养老金较长的投资期限也使得DC型养老金的投资管理问题更复杂，在投资过程中不仅要考虑利率风险和随机波动率，还要考虑通胀风险和工资水平风险。Yao Haixiang等[8]研究了在多周期均值—方差框架下DC型养老金的资产配置问题，考虑了随机工资和死亡率风险，利用随机最优控制方法，得到有效的投资策略和有效边界的解析表达式。Sun Jingyun等[9]在DC型养老金最优投资组合的均值—方差模型中，考虑了通胀风险和随机工资。Njoku等[10]在仿射利率模型下，研究了随机工资对DC型养老金最优投资策略的影响。Chen Zheng等[11]在DC型养老金最优投资问题中，重点引入了通胀风险和长寿风险，并通过数值方法探讨了这两种风险对最优策略的影响。刘渝琳等[12]为在养老金投资过程中有效规避通胀风险，给出了风险中性测度下通胀指数债券的定价，并分析了通胀指数债券对通胀风险的对冲作用。

上述关于DC型养老金投资管理的研究中都未考虑养老金管理者向参保人收取管理费用的问题，而在DC型养老金的投资管理过程中，养老金管理者需要向参保人收取一定的管理费用，这个管理费用对个人养老金账户的终端财富具有显著的影响。Whitehouse[13]在对13个国家的养老金管理费用效应进行评估比较之后，得出结论：每收取1%的管理费用，养老金的终端财富价值就会增加将近20%。Murthi等[14]研究表明，在英国收取养老金管理费用以及其他费用，会使得个人养老金账户的财富价值减少超过40%。已有关于养老金管理费用的研究已经对DC型养老金计划的这个特性进行了论证，因此研究养老金管理机构对参保人收取管理费用的方式对于养老金的投资管理是具有现实意义的。正如Kritzer等[15]所指出，养老金管理者对参保人收取管理费用一般有三种方式：按比例在个人养老金账户资产财富中收取、按比例在工资中收取以及按比例在超额收益中收取。按资产财富与工资比例收取养老金管理费用是在拉美国家最主流的两种方式，目前，对于比较这两种收费方式的研究较少。Chávez-Bedoya[16]在对按资产财富比例和按工资比例两种收费方式下的终端确定等价财富进行比较之后，得到了一个等价管理费用，它相当于参保人参加DC型养老金的固定费用，揭示了两种收费方式的关系。本文在文献[16]的研究基础上，用Heston随机波动率模型来刻画金融市场，选取CRRA效用函数和CARA效用函数，以最大化参保人终端财富值的期望效用为目标，继续研究这两种养老金管理费用收费方式之间的关系，得到两种效用准则下的等价管理费用。

本文的主要创新点有如下两点：(i)考虑Heston模型描述的风险资产(股票)，增加了风险资产随机波动率对养老金投资管理的影响，将已有研究中用Black-Scholes模型描述的金融市场拓展至更为合理的Heston模型完备金融市场。Heston随机波动率模型可以更好的解释金融市场里面尖峰厚尾的现象，但引入Heston模型会加大求解等价管理费用的难度，最主要的难度就是Heston模型所带来的随机变量v能否和随机变量财富过程x分离，将求解等价管理费用时得到的HJB偏微分方程转换为常微分方程来求解，这也是本文与已有研究面临问题的不同之处。(ii)分别在CARA和CRRA两种效用准则下考虑参保人的风险偏好，参照两种风险偏好下的等价管理费用，有利于决策。众所周知，在一个完善的养老体系中，参保人之间具有不同的风险偏好，若仅仅在一种效用准则下来研究等价管理费用，其结论的适用性将存在一定局限性。相比已有研究仅仅考虑CARA效用准则，本文考虑的更为全面，拓展了结论的适用范围。本文的主要结论将为DC型养老金管理者收取管理费用和精准投资提供参考，为参保人缴纳管理费用提供指导，为养老金管理费用政策制定者提供依据。

2 模型设定及条件假设

在本节，我们首先介绍金融市场结构，然后给出DC型养老金终端财富的随机动态过程。

2.1 金融市场

假设DC型养老金计划投资的金融市场由两种金融资产组成，一种无风险资产(银行账户存款)和一种风险资产(股票)。银行账户存款价格动态过程满足如下常微分方程：

dS0(t)=rS0(t)dt,S0(0)=s0>0

(1)

式中r>0表示无风险利率。风险资产(股票)的价格过程满足经典的Heston模型：

dS1(t)=S1(t)[(r+ηV(t))dt

S1(0)=s1>0

(2)

V0(0)=v0>0

(3)

其中η,k,θ,σ都为都为大于零的常数，满足2kθ>σ2，以保证对任意t∈[0,T]，有V(t)>0。Ws(t)与Wv(t)是两个标准布朗运动，它们之间的相关系数是ρ，即E[Ws(t)Wv(t)]=ρt，ρ∈[-1,1]。

2.2 DC型养老金财富过程

在积累期[0,T]中，参保人定期按工资的固定比例缴纳保费，本文假设固定的缴费率为常数ε，工资为单位1。在这个阶段，养老金管理者将账户资金投资于银行账户存款与股票中，假定在时刻t投资于股票的比例为π(t)，则投资于银行账户存款的比例为1-π(t)。定义X(t)为养老金财富过程，若养老金管理者不向参保人收取任何管理费用，则财富过程变化过程服从如下随机微分方程：

dX(t)

X(0)=x0

(4)

将式(1)和式(2)带入(4)中，可得财富过程：

dX(t)={X(t)[r+ηV(t)π(t)]+ε}dt

X(0)=x0

(5)

现在来考虑养老金管理者向参保人收取管理费用的两种情形，一种是按资产财富比例收取，另一种是按工资比例收取。首先考虑前者，假定δ>0为每月在资产财富中收取管理费用的比率，则收取的管理费用为δX(t)。引入该部分后，财富过程为：

Xs(0)=x0

(6)

再考虑按工资比例收费情形，这也可以称为按保费比例收费，因为是在作为保费的那部分工资中收取管理费用。当养老金管理者未向参保者收取管理费用时，参保人每月向养老金账户按工资比例缴纳ε的保费。现参考文献[16]的研究，定义α>0为按工资比例缴纳养老金管理费用的代表参数。则参保人每月应向养老金管理者缴纳管理费用F=(1-e-α)ε，因此参保人每月向账户缴纳的保费部分就剩余e-αε。由此可得该情形下财富过程为：

Xf(0)=e-αx0

(7)

需要注意的是：在此情形下，X0并不能表示养老金账户财富的真实值，而需要通过机会成本(缴纳管理费用)来调整为e-αx0。

3 等价管理费用的求解

在本节，我们将求解等价管理费用。首先对优化问题进行描述，其次分别在CARA和CRRA效用准则下求解三种情形下的最优投资策略和值函数的解析式，最后对两种收费方式的终端确定性等价财富进行比较，得到两种效用准则下的等价管理费用。

3.1 最优化问题

本文涉及三种情形的优化问题，分别是无管理费用、按资产财富比例收取管理费用以及按工资比例收取管理费用，具体表述如下：

(i)无管理费用情形

(ii)按财富比例收取管理费用情形

(iii)按工资比例收取管理费用情形

+ρθvxπ(t)Hxv}=0

其中Ht,Hx,Hv,Hxx,Hvv,Hvx分别表示H对t,x,v的一阶和二阶偏导数。

根据一阶条件得到最优投资策略：

(8)

将式(8)带入到HJB方程中，可得：

(9)

其边界条件为H(T,v,x)=U(x)。

根据类似的方法，本文可以得到其他两种情形下对应值函数的HJB方程，再根据一阶条件，得到对应的最优投资策略的形式解。囿于篇幅所限，在此不再赘述。

3.2 CARA效用准则下的等价管理费用

同以上得到最优投资策略和值函数的形式解一样，这部分首先求解无管理费用情形下的最优投资策略和值函数的解析式以及终端确定性等价财富，然后再采用类似方法得到其他两种情形下的最优投资策略和值函数的解析式以及终端确定性等价财富。

3.2.1 无管理费用下终端确定性等价财富

H(t,v,x)

(10)

其边界条件为m(T)=1，g(T)=0，h(T)=0。由此可以得到方程(9)中值函数的各阶偏导数：

Ht=-c[mt(x-g(t))-gtm(t)+vht]H

Hx=-cm(t)H,Hxx=c2m2(t)H,

Hv=-ch(t)H,

Hvv=c2h2(t)H,Hxv=c2m(t)h(t)H.

将上述偏导数带入到方程(9)中，可得：

(mt+rm(t))x

(11)

对方程(11)进行拆分，可得下述三个常微分方程：

mt+rm(t)=0,m(T)=1

(12)

(13)

×(1-ρ2)h2(t)=0,h(T)=0

(14)

结合各函数的边值条件，解得：

m(t)=er(T-t)

(15)

(16)

g(t)

(17)

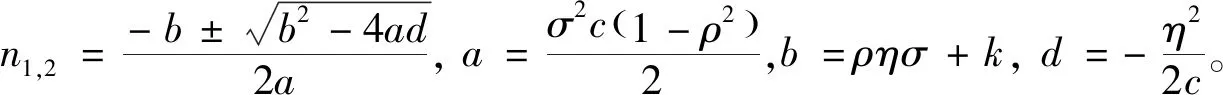
至此，已求得无管理费用情形下值函数的解析式：

H(t,v,x)

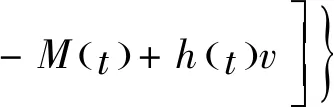
(18)

式中：

同样地，将值函数的解析式带入到式(8)中，可以得到该情形下最优投资策略的解析式：

(19)

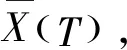
(20)

此外，为了后文比较方便，特在此定义终端确定性等价财富为：

(21)

式中：

M(0)

3.2.2按财富比例收费下的终端确定性等价财富

类似于无管理费用时的求解方法，可得按财富比例收费时的最优投资策略和值函数的解析式为：

(22)

(23)

该情形下对应的终端确定性等价财富为：

(24)

3.2.3 按工资比例收费下的终端确定性等价财富

采用类似方法可得考虑按工资比例收费时的最优投资策略和值函数的解析解为：

(25)

(26)

该情形下对应的终端确定性等价财富为：

-M(0)+h(0)v0

(27)

3.2.4 等价管理费用

为了让参保人知道哪种方式更优，需要比较两种收费方式。由于参保人期望养老金账户终端财富效用最大，本文在这里比较两种收费方式下的终端确定性等价财富。参考文献[16]，定义如下比例：

(28)

当Rsf>1时，参保人更倾向于按资产财富比例缴纳管理费用；当Rsf<1时，参保人更倾向于按工资比例缴纳管理费用；当Rsf=1时，两种收费方式都一样，都能接受。

本文假定养老金账户在积累期的初始时期资金为0，即x0=0。在此假设条件下，可以得到：

Rsf

(29)

定义该比例的目标是为了在两种收费方式中找到一个平衡点，即本文所说的等价管理费用。在此给定α*，令在资产财富中收取管理费用的比例δ*为等价管理费用，当该比例等于1时，可得：

(30)

从式(30)可以看出，等式左边表示T时刻e-δ*T比例的连续养老金在利率为r-δ*时的未来价值，而等式右边表示T时刻e-α*比例的养老金在利率为r时的未来价值。现定义养老金的未来价值为e-δ*TSr-δ*和e-α*Sr，则由式(30)可得：

(31)

由式(31)可知，等价管理费用δ*只与r,T和α*有关，并随r和T增大而减小。

这里简要说明将上述风险偏好满足CARA效用函数的特殊情形下的等价费用拓展至风险中性的情形下。定义风险中性测度Q下的比例为：

(32)

当Nsf>1时，参保人更倾向于按资产财富比例缴纳管理费用；当Nsf<1时，参保人更倾向于按工资比例缴纳管理费用；当Nsf=1时，两种方式都能接受。

在风险中性测度Q下，无风险资产和风险资产的利率都为r，有η=0。则M(0)=0，h(0)=0，最大化期望终端财富为：

(33)

(34)

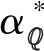
3.3 CRRA效用准则下的等价管理费用

类似于CARA效用准则，本节用同样的求解方法可以得到CRRA效用准则下无管理费用以及两种收费模式下的最优投资策略、值函数的解析式和终端确定等价财富。

3.3.1 无管理费用下终端确定性等价财富

(35)

具体的求解过程在此不再赘述，通过相似的方法可以得到无管理费用下的值函数和最优投资策略的解析式：

(36)

π*(t)

(37)

式中：

在CRRA效用准则下无管理费用的最优化问题已得到解决，接下来需要决定养老金终端确定性等价财富。由于前文已定义了最优投资策略所决定的期望效用最大化的终端财富，所以终端财富的最大化期望效用为：

(38)

则相应的确定性等价财富为：

(39)

式中：

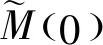
3.3.2 按财富比例收费下的终端确定性等价财富

同无管理费用时的求解方法，可得到考虑按财富比例收费时的最优投资策略和值函数的解析式为：

H(t,v,xs)

则该情形下对应的终端确定性等价财富为：

3.3.3 按工资比例收费下的终端确定性等价财富

类似地，得到考虑按工资比例收费时的最优投资策略和值函数的解析式为：

H(t,v,xf)

则该情形下对应的终端确定性等价财富为：

3.3.4 等价管理费用

该比例大小所代表的意思同CARA效用下定义的比例一致。

本文假定养老金账户在积累期的初始时期资金为0，即x0=0。在此假设条件下，可以得到：

(40)

同样地，为了得到等价管理费用。在此，我们给定α*，令在资产财富中收取管理费用的比例δ*为等价管理费用，当该比例等于1时，可得：

(41)

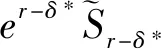
(42)

从等式中可知等价管理费用δ*只与r,T和α*有关，并随r和T的增大而增大。

此处也简要说明将上述风险偏好满足CRRA效用函数的特殊情形下的等价费用拓展至风险中性的情形下。定义风险中性测度Q下的比例为：

该比例大小所代表的意思同CARA效用下定义的比例一致。

(43)

(44)

4 算例分析

这一部分，我们通过数值算例来分析模型的关键参数对等价管理费用的影响以及等价管理费用对财富过程的影响，并验证上述理论推导所得结论：取等价管理费用时，两种收费方式达到一种平衡，参保人两种收费方式都能接受。

模型中的参数参考文献[16]的设置，假定参保人的退休年纪为65岁，积累时间具体可由等式T=(65-E)×12表示，其中E表示参保人年龄。养老金管理者按工资比例收费取三种比例：fmin=1.47%，favg=1.58%，fmax=1.69%。类似地，考虑一部分强制费用，根据关系α=-ln(1-10f)，可得到：αmin=0.159，αavg=0.172，αmax=0.185。其他相关参数的设定为：k=1，c=0.1，θ=0.02，η=1，σ=0.08，ε=0.12，ρ=0.5，x0=0，v0=0.02，p=0.3，r=0.05。

4.1 CARA效用准则下算例分析

首先来考虑在CARA效用下等价管理费用随参保人年龄的变化。由图1，一方面我们可知在CARA效用准则下，等价管理费用随参保人的年龄E严格递增，随积累时间T严格递减；另一方面，当固定参保人年龄E或积累时间T时，等价管理费用δ*随α或f严格递增。这变化趋势与文献[16]的结论是一致的，但本文中等价管理费用的变化增量以及数值结果要远远小于文献[16]中的增量及数值结果，也可以理解为管理费用越少，耗费的成本也就越低。这是本文引入Heston模型所带来的不同之处，在更为合理的Heston模型完备金融市场中，对于养老金管理者制定更合理精确的管理费用水平是有一定现实参考意义的。若考虑参保人年龄为30岁时，按工资比例收费时代表参数αavg=0.172，对应的等价管理费用为δ*=0.0821%；当δ*>0.0821%时，对于参保人而言，按工资比例缴纳管理费用更有优势。

可以看出等价财富δ*>0.0585%，在任何情况下都需满足，若小于该值，则按工资比例缴纳管理费用更有优势。

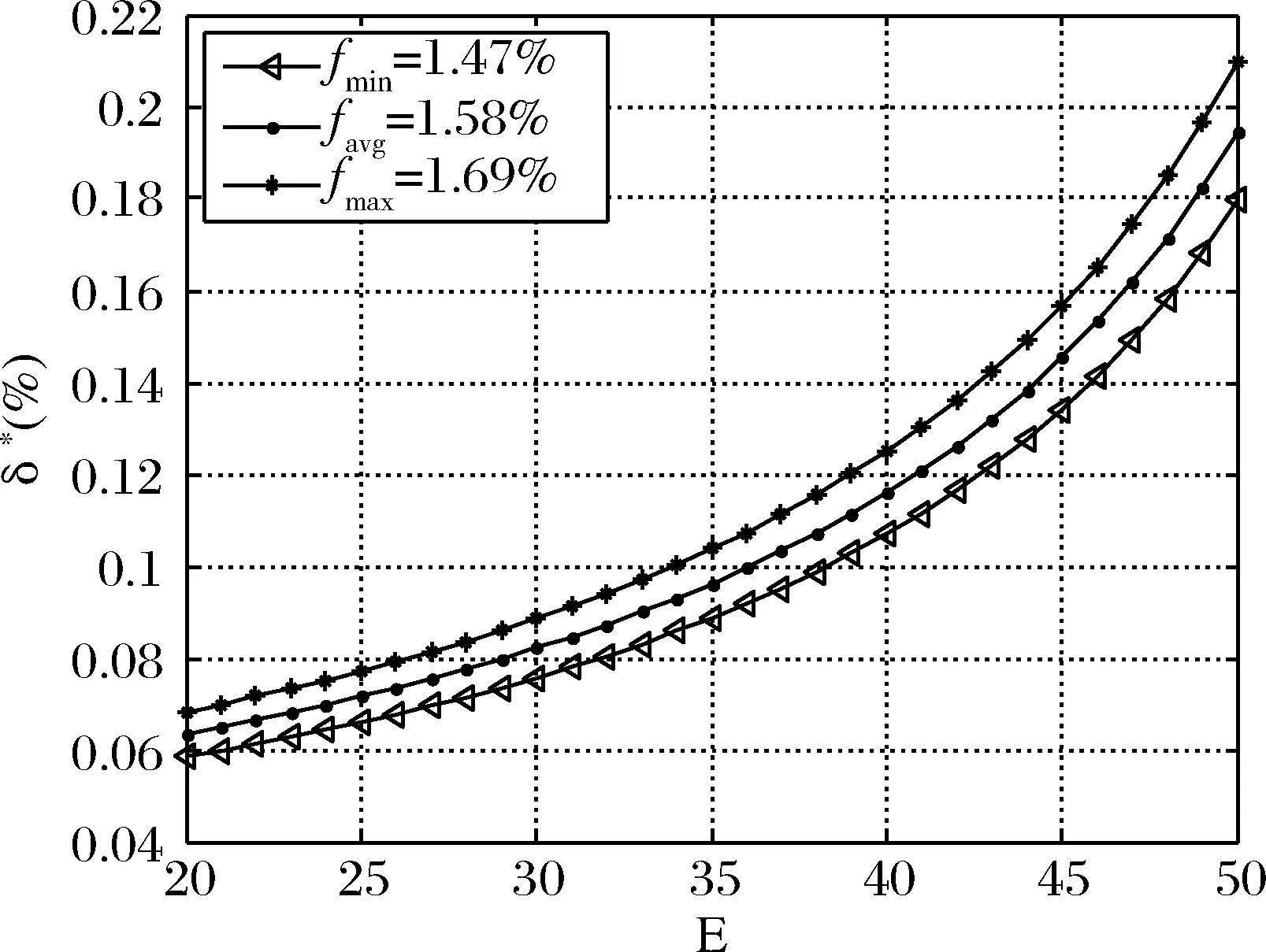
图1 CARA效用下等价管理费用随参保人年龄变动

其次，我们考虑等价管理费用对财富过程的影响。在CARA效用准则下，选取年龄为50岁时的等价费用δ*=0.19%，对应的αavg=0.172，将无管理费用和两种收费方式下的最优投资策略带入对应的财富动态过程中，有图2和图3。对于财富的动态过程，我们可以得到两种情况。一种是收取等价管理费用会使养老金账户财富值减小，如图2所示；另一种是收取等价管理费用会使养老金账户财富值增加，如图3所示。这种情况的出现归因于不同的养老体系，有的养老体系中个人养老账户过于分散且具有较高的复杂性，会产生很高的账户管理成本，这使得管理费用的收取超过了一定的数额，导致个人财富的大量流失，详细的成因可参考文献[13]和[14]。从图2与图3中可知，无论是等价管理费用使参保人增加还是减少的情况，两种收费方式的财富动态过程都是基本重合的，拟合度较高。这说明，只要所取得管理费用为等价管理费用，按资产财富比例与按工资比例收取管理费这两种收费方式都是一样的效果，这正验证了本文的理论推导。

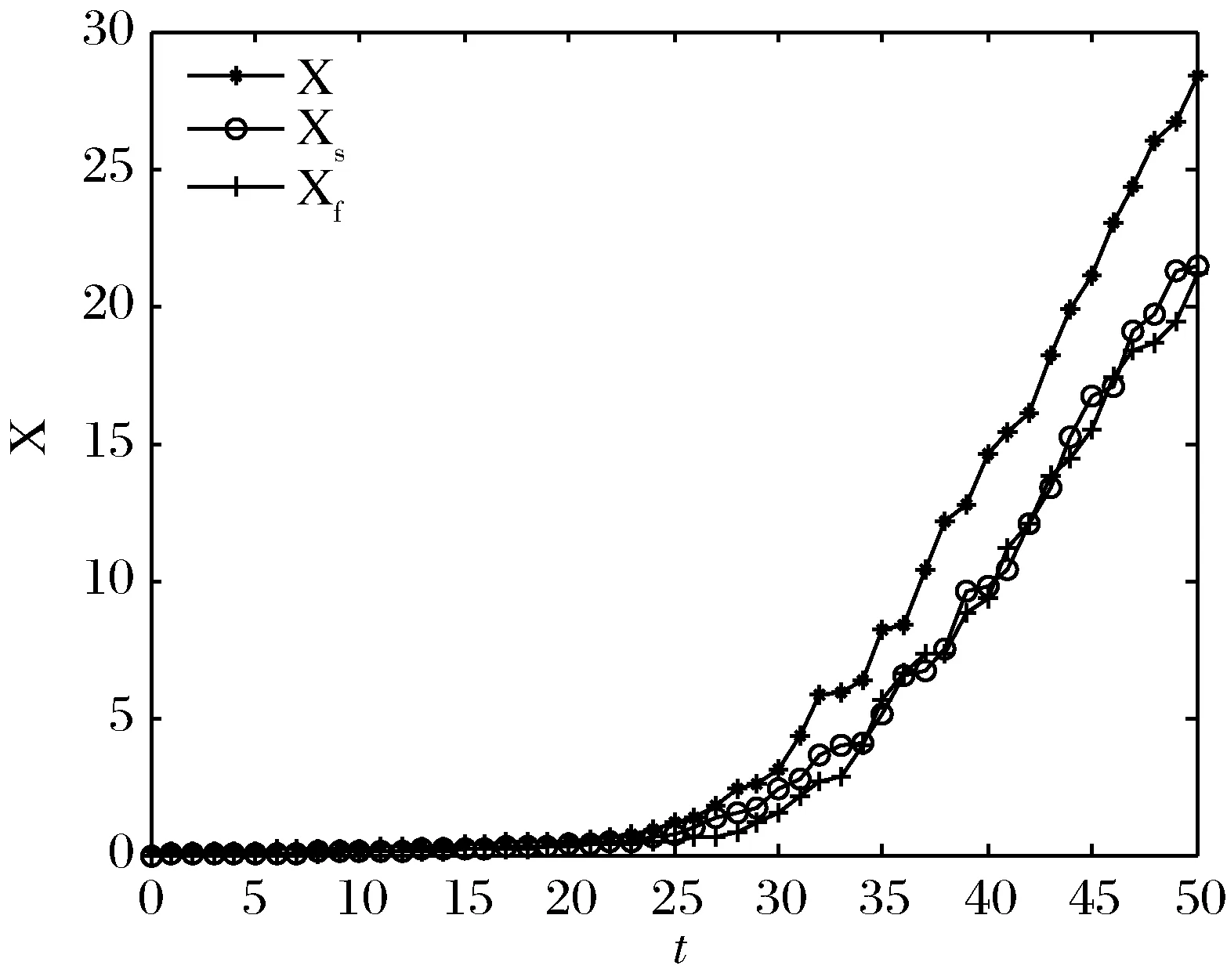
图2 CARA效用下财富动态过程情形一

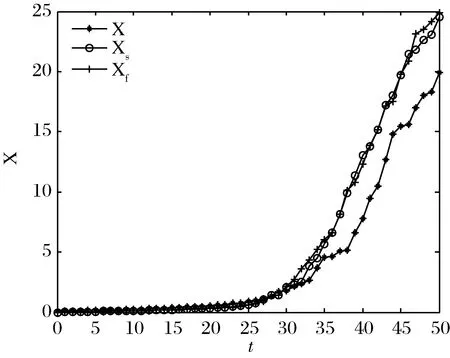
图3 CARA效用下财富动态过程情形二

4.2 CRRA效用准则下算例分析

同CARA效用准则一样，先考虑CRRA效用下等价管理费用随参保人年龄的变化。由图4，我们可知在CRRA效用准则下，等价管理费用随参保人的年龄E严格递减，随积累时间T严格递增。当固定参保人年龄E或积累时间T时，等价管理费用δ*随α或f严格递减，这正好和CARA效用准则下相反。这可能是由于在CRRA效用下，随着瞬时财富水平的增加，参保人对于风险的厌恶程度会下降。当参保人的财富随着年龄的增长不断积累，其对风险的厌恶程度会下降，这就会使得养老金管理者降低风险规避水平，进而会降低管理成本，因此管理费用呈下降趋势。其他的比较在此不再赘述，可参考CARA效用情形。

图4 CRRA效用下等价管理费用随参保人年龄变动

其次，我们考虑等价管理费用对财富过程的影响。在CRRA效用准则下，选取年龄为50岁时的等价费用δ*=0.1%，对应的αavg=0.172，将无管理费用和两种收费方式下的最优投资策略带入对应的财富动态过程中，有图5和图6。类似地，CRRA效用下财富动态过程的趋势同CARA效用情形下一样。且等价管理费用对养老金账户财富值既有正的影响，也有负的影响。取等价管理费用时，两种收费方式的效果一样，达到一个平衡，具体表现在图5与图6中：两种收费方式下的财富动态过程曲线拟合度较高。

图5 CRRA效用下财富动态过程情形一

图6 CRRA效用下财富动态过程情形二

5 结语

鉴于目前对DC型养老金管理费用收取方式的研究不多，本文在文献[16]的研究基础上，考虑风险资产价格动态过程服从Heston模型。首先分别在CARA效用准则和CRRA效用准则下得到了无管理费用、按资产财富比例收取管理费用以及按工资比例收费三种情形的最优投资策略和值函数的解析式；其次再对比两种收费方式下的终端确定性等价财富，得到了两种效用准则下的等价管理费用，并将其拓展至参保人风险偏好为中性的情形下，证明了风险中性情形下的管理费用适用范围更广；最后通过数值算例分析了参保人年龄对等价管理费用的影响，以及等价管理费用对养老金账户财富的影响。本文主要研究发现：(1)在CARA效用准则下，等价管理费用随参保人年龄严格递增，而在CRRA效用准则下，等价管理费用随参保人年龄严格递减。(2)无论是在CARA效用准则还是CRRA效用准则下，等价管理费用对养老金账户财富的影响既有正面的，也有负面的。(3)CARA效用准则与CRRA效用准则下，取定等价管理费用后，两种收费方式的效果都是一样的。

本文对于在两种收费方式中寻找一个平衡点(等价管理费用)的方法是具有现实意义的，可以为参保人缴纳管理费用和养老金管理者收取管理费用提供指导，养老金投资者在进行投资时参考这部分的等价管理费用，能更准确的进行投资。然而，本文的研究尚有不足，随着金融市场的不断复杂化，投资人在进行养老金投资时所面临的风险也愈加多样化，随机工资、随机利率、通货膨胀、长寿风险等等，若考虑这些因素，对最优投资策略、值函数以及等价管理费用的求解会加大难度。其次，由于本文是在效用准则框架下进行的，而在均值—方差以及其他风险准则下得到的结果和本文有何区别，这方面的研究也尚未发现。此外，考虑到管理费用收取问题，如果能从管理者和参保者的委托-代理关系出发，建立一些新的优化目标，也是非常有价值的研究题目。这些都是我们未来研究的方向。