差分方程描述下的系统性质判定的有效办法

文/吴令军 周子瑄 刘莎莎

1 系统性质的定义与判别方法说明

一个离散时间系统是将输入序列x(n)变换成输出序列y(n)的一种运算，记为y(n)=T[x(n) ]。时域离散系统中主要讨论系统的线性、时不变性、因果性和稳定性，因此如何判断系统的线性、时不变性、因果性和稳定性就显得十分重要。对四种系统特性进行分析并给出判断方法，并指出了每种判断方法所适用的情况。通过灵活运用这些方法，可以快速而准确的判断系统的特性。根据文献给出如下定义与判定方法。

（1）线性系统的定义是指系统的输入输出满足线性叠加原理，其判别公式如下。

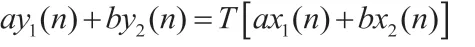
（2）时不变系统的定义是输入信号的移位会引起输出信号的移位，其判别公式如下。

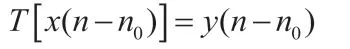
（3）因果系统的定义是指n时刻的输出只取决于信号输入系统前的值，而与输入时刻后的值无关。判别方法是当n<0时，h(n)=0，则为因果系统。

（4）稳定系统：若系统对任意的有界输入均产生有界的输出，则表明为稳定系统。其判别方法为用叠加性原理求系统的稳定输出，使得单位抽样响应满足绝对可和条件，即满足公式

2 传统解法与主推算法

由线性时不变系统的差分方程并不能直接推出此系统是线性的，一个常系数线性差分方程，只有当边界条件选的合适，才相当于一个线性时不变系统。因此，边界条件很重要。以下举个通例：

常系数线性差分方程 ，当边界条件 时，求该系统是否满足线性时不变和因果稳定性。

2.1 传统解法：递推法验证

通过求解单位抽样响应来证明该系统的线性和时不变性，而求解单位抽样响应采用的方法为迭代法。单位抽样响应的输入为单位抽样信号，即 ，分别用单位抽样信号的移位序列表示为输入，即令

具体步骤如下：

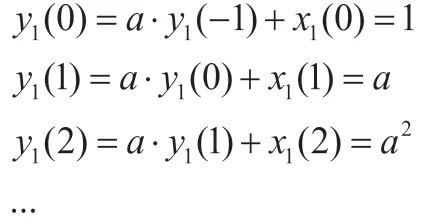
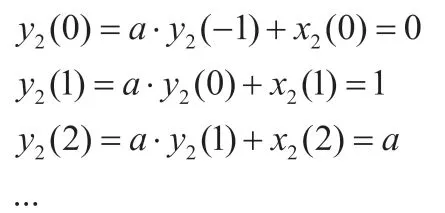
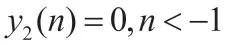
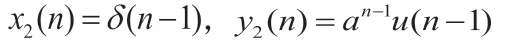
令x3(n)=x1(n)+x2(n)=σ(n)+δ(n-1)，y3(-1)=0

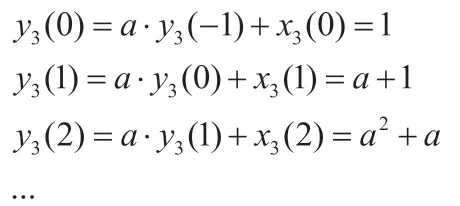
因此，系统是线性系统，综上所述系统为线性时不变系统。

2.2 主推做法

先对差分方程进行z变换，再对系统的线性时不变等性质进行判定。（同时系统函数零极点与收敛域关系也可判定）

因，对于差分方程如果输入是 这一特定情况，响应就是单位抽样响应，所以这对于判定因果稳定性很有必要。可令 。正如前面所说边界条件很重要，即与初始条件有关，故我们研究的是零输入解，而不是零状态解，而在求零输入解时，考虑到初始条件，用单边Z变换。

【注：单边变换定义：如果x(n)的存在范围是0 ～+∞，则为，称单边z变换，特别的，单边Z变换的时移性质：

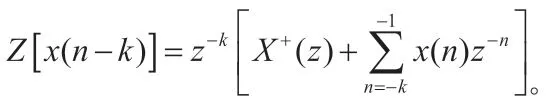
我们对应的取 ，此处可将δ(n)看成特殊右边序列，有

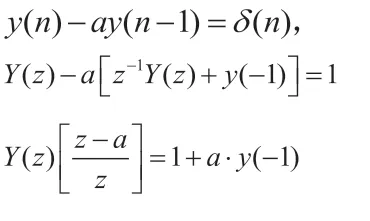
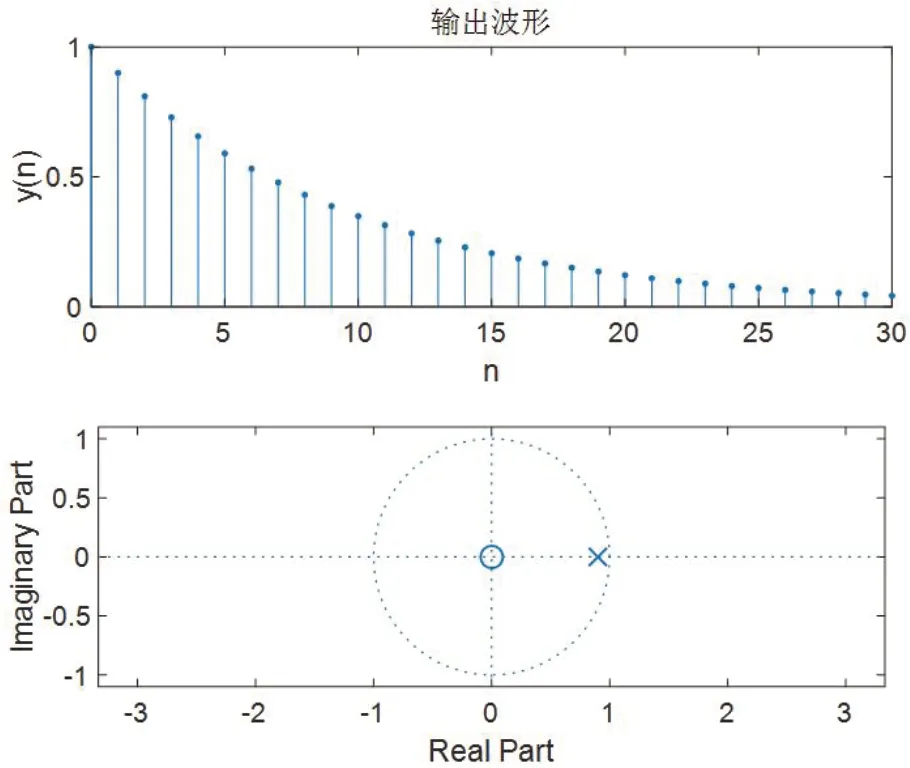
图1

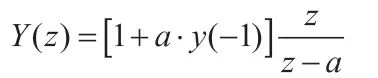
边界条件为 ，因此

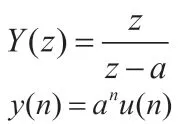
所以是因果系统

（3）：

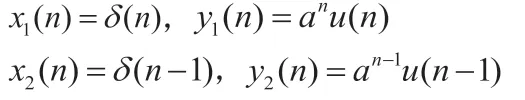
x1(n)和x2(n)为移一位关系，且y1(n)和y2(n)也对应移一位关系，因此系统为时不变系统。

（4）：

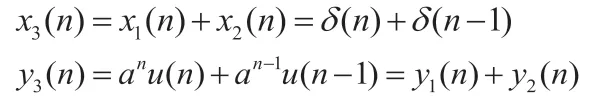
因此系统是线性系统。

同样可以证明出这个方法对于不同初始条件y(-1)=-1等都适用，同时，也具有一般性，如常见题型y(n)-0.9y(n-1)=0.05u(n)，初始条件y(-1)=-1，有兴趣的读者，自己可以尝试做做。

3 根据系统函数的零极点分布及收敛域的关系

（1）线性非移变系统稳定的充要条件是系统函数H(z)的收敛域包含单位圆。

（2）线性非移变系统稳定的因果条件是系统函数H(z)的收敛域包含∞

（3）一个因果稳定系统其系统函数的极点必须在单位圆内。

（4）一个因果稳定系统其系统函数的收敛域一定从单位圆内到无穷大处。

4 MATLAB验证解法正确性

常系数线性差分方程 ，当a=0.9，边界条件 ，时，代码如下所示。

%%输入序列xn，输出序列yn，

a = 0.9 ;ys=0; %ys表示边界条件y(-1)=0

xn = [1,zeros(1,30)]; %假定输入序列xn

B=1;A=[1,-a]; %差分方程系数

xi=filtic(B,A,ys);%xi为滤波器传递函数的分子系数和分母系数。

yn=filter(B,A,xn,xi);%yn为滤波器输出

n=0:length(yn)-1;

subplot(2,1,1);stem(n,yn,'.') %绘制输出波形

title('输出波形');xlabel('n');ylabel('y(n)');

subplot(2,1,2);zplane(B,A) %绘制零极点图。如图1所示。

5 总结

传统解法与推荐解法的优缺点对比，对于离散时间系统的线性时不变性，因果稳定性的判定尤为重要，对于常见类型的，可以直接根据定义法判别，用差分方程表示的，可根据以上两种方法求解，后一种可能更便捷。