时滞基因调控网络的鲁棒指数稳定性分析
王艳艳,汪忠志
(安徽工业大学数理科学与工程学院,安徽马鞍山243032)
基因调控网络是一种复杂多变的非线性动态网络系统,通常能呈现出复杂的动力学行为,Jacob 等[1]和Monod等[2]提出的调控模型一般被视为最早的基因调控网络模型。迄今为止,关于基因调控网络的动力学研究取得了许多成果[3-10]。Li等[3]考虑生物现象中的时滞问题,给出了时滞基因调控网络模型,并给出判定此模型渐近稳定性的判据。此外,在基因调控网络的处理过程中,有一些不能人为控制的不确定性因素,如系统参数的波动、外部因素的干扰等,这些均会导致网络的不稳定性。一个稳定的网络应具有鲁棒性,鲁棒稳定性的研究更贴合实际网络,Wang等[4]研究了带有噪音扰动项的基因调控网络的幂律鲁棒稳定性;赖强等[5]对于一类简单基因调控网络的动力学行为进行了理论和数值分析,给出了保证该网络的双稳定性和分叉存在的条件;Ren等[6]给出判别不确定基因调控网络模型的鲁棒稳定性的充分条件。本文首先以矩阵方程的形式建立基因调控网络,在网络系数不确定但范数有界的条件下,分析其鲁棒指数稳定性。
1 基因调控网络模型的建立
文献[11]提出了如下基因网络:

其中:Mi(t)和Pj(t)分别为信使RNA(ribonucleic acid)和蛋白质浓度随时间变化的函数;ai和ci分别为信使RNA和蛋白质的降解率;di是转录速度;ε(t)和τ(t)分别为翻译时滞和反馈调节时滞;Gij为第i 个基因在转录过程中受到第j 个蛋白质的反馈调节作用的函数,是一种单调的s 型函数,当转录因子j 是激活因子时,该函数是递增的,当为抑制因子时,该函数递减。而Hill函数恰有这种性质。

其中:Hj为Hill系数;βj是正常数;bij也是常数,并且是有界的,表示转录因子j 对目标基因i 转录过程中的最大转录速率。这样网络(1)就可以写成:

其中:


考虑到参数不确定性的实际存在,本文研究网络(5)。


在式(5)中τ(t)是有界的时间延迟,满足0 ≤τ(t)≤τ,并且有:

初始条件如下:

其中:φi(s),ψi(s),是[-τ,0]有界且连续的函数;i=1,2,…,n。矩阵ΔA(t),ΔC(t),ΔD(t),ΔW(t)有如下形式:



引理2[13]给定合适维数的矩阵Q=QT,H,E 对于所有满足FTF ≤I 的矩阵F,有Q+HFE+ETFTHT<0成立等价于存在一个常数ε >0 使得Q+εHHT+ε-1ETE <0 成立。
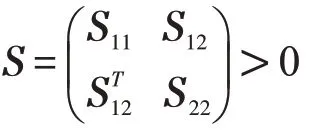
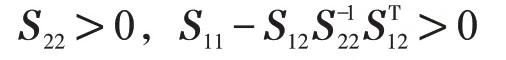
其中

2 鲁棒指数稳定性分析
上节已将网络通过矩阵方程的形式构建起来,本节将构造合适的Lyapunov-Krasovskii 泛函,对延时基因调控网络(5),应用矩阵不等式方法,得出保证其鲁棒指数稳定性的条件。


其中k=max{k1,k2,…,kn},网络(5)是全局鲁棒指数稳定的。
证明当线性矩阵不等式(9)与(10)成立时,对充分小的常数α >0 有如下的矩阵不等式成立:
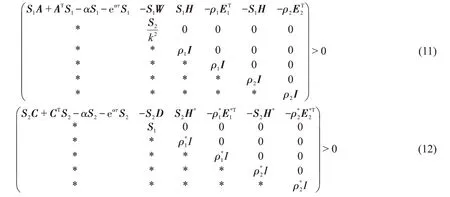
当t ≥0 考虑式(13)的Lyapunov函数
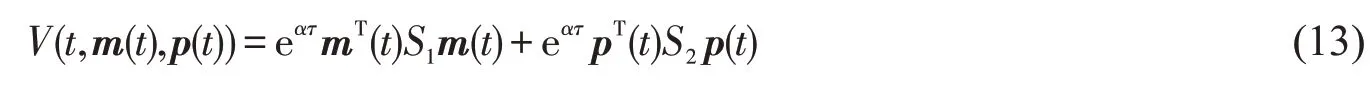

由式(6),有不等式(15)成立。

同理可得
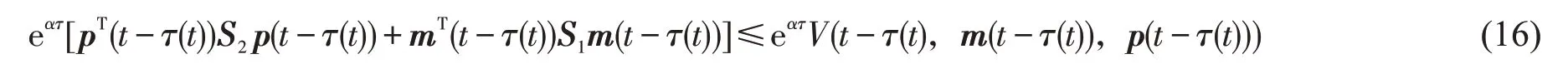
从而可以得到
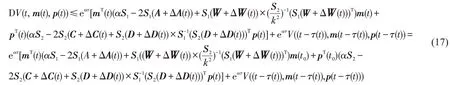
借助V((t-τ(t)),m(t-τ(t)),p(t-τ(t)))≤β(t)=V(t,m(t),p(t),考虑到τ 与α 都是常数,得

借助引理2和Schur补引理(引理3)及不等式(11)~(12),得

同理
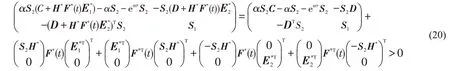
继续使用Schur补引理(引理3),以上两个不等式变形为:

得到DV(t,m(t),p(t))≤0,与假设矛盾,因此β(t)是非增的。
故∀t ≥0,有β(t)=β(0)由β(t)的定义,得到:

根据式(13)又得

综上可得

式(25)即表明了所考虑的基因调控网络时指数稳定的。
注1:定理所给的条件保证了所考虑网络是按照指数速度收敛到平衡点的,收敛速度是由α 决定的,而α的取值范围可由证明过程中的式(11)~(12)估计出。
3 算例仿真
在网络中按照文献[3]取值如下:
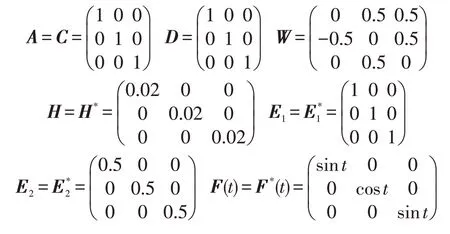

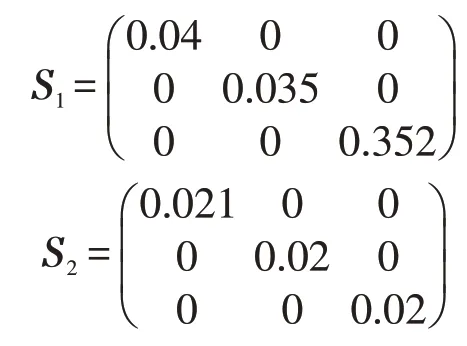
使式(9)~(10)成立。
信使RNA和蛋白质浓度即Mi(t)和Pi(t)轨迹图如图1。

图1 Mi(t)和Pi(t)的轨迹图Fig.1 Trajector of Mi(t)and Pi(t)
由图1知所考虑网络状态与平衡点的差皆趋向于零,即网络是全局鲁棒指数稳定的,而要找的两个正定矩阵S1,S2也通过仿真给出了具体的数值,说明两个正定矩阵真实存在。
3 结 论
对有范数有界的不确定性因素的延时基因调控网络的鲁棒指数稳定性问题进行了理论研究和数值分析。在理论研究中,用矩阵方程表示研究的网络,在此基础上借助李雅普诺夫(Lyapunvo)函数、Schur 补引理、矩阵的相关结论和线性矩阵不等式方法,得出只要两个分块正定矩阵存在,网络的鲁棒指数稳定性就可以得到保证。在数值分析式时,利用MATLAB LINERA MATRIX INEQUALITY工具箱,找到了具体的理论分析中需要的正定矩阵。现阶段基因调控网络的各种动力学行为引起了许多学者的关注,探索如何在白噪声干扰下保证基因调控网络的稳定性是后续工作的方向。

