自由活塞斯特林发电机空载磁场模拟及分析

陈 曦， 崔 浩

（上海理工大学 能源与动力工程学院， 上海 200093）

自由活塞斯特林发电机是将自由活塞斯特林发动机和直线发电机耦合在一起构成的，具有热电效率高、寿命长等优点，能满足能源高效利用和环境安全的需求。其中，直线发电机与旋转电机相比，结构简单、灵敏度高、定位精度高、反应速度快[1]。由于斯特林发动机与直线发电机没有中间传动环节，从而减小了机械损耗，提升了机械效率。

按驱动方式，直线电机可分为动圈式、动铁式和动磁式。动磁式直线电机相对于动圈式和动铁式，具有结构紧凑、体积小、比推力大、效率高、可靠性高等优点，所以动磁式直线电机更适用于自由活塞斯特林发电机中[2]。在动磁式直线电机中，依据绕组相数可分为单相和三相动磁式直线电机。本文基于复杂性和成本考虑，采用单相动磁式直线电机。

对动磁式直线电机的数学模型进行分析的方法主要有两种：磁路分析法和有限元法。由于实际磁路结构、边界和材料等的复杂性和非线性，需要对实际磁路进行一系列的假设和简化，因此想要通过磁路分析法进行精确解析非常困难，分析结果误差较大，这种方法多用于直线电机的初步设计。而有限元数值解析法可以借助电磁场软件对材料的非线性、结构的复杂性进行精确处理，计算结果精确，因此有限元数值分析方法主要用于直线电机的优化设计。

Thales 公司的Benschop 等[3]利用Opera 电磁分析软件对一台单磁钢双线圈电动机进行了电磁模拟与结构优化。英国Sheffield 大学的Clark 等[4]设计了一台双线圈双磁钢动磁式直线电动机，应用等效电路法对铜损、线圈匝数、电感等电磁参数进行了初步设计，然后将系统等效为一个非线性变压器模型，通过有限元分析进行了电动机参数的精确设计。日本的Takahashi 等[5]在未进行解析模型建立与计算的基础上，直接通过有限元分析对一台直流线性电动机进行了优化设计，这一方法可以满足一定的准确性要求。上海交通大学陈楠[6]采用Ansoft Maxwell 电磁场分析软件对直线电动机的动态和静态电磁特性进行了数值模拟，揭示了动磁式直线电动机电磁力产生的机理。浙江大学周文杰[7]使用Ansys 电磁场分析软件对其设计的动圈式直线电动机进行了结构分析和优化，得出了结构尺寸和气隙厚度对电动机推力的影响。华中科技大学张春平等[8]运用等效磁路原理推导了电动机线圈磁匝链的表达式，然后根据电磁能守恒原理，将电动机系统简化为一个无损的磁储能系统，通过解析方法，推导了线圈静态感性阻抗和推力系数的表达式，从能量角度解释了电学部分与机械部分的耦合原理。赵镜红等[9]针对径向充磁圆筒永磁直线同步电机，介绍了一种基于圆柱坐标标量磁位的分离变量法的磁场解析计算方法，并对大气隙无槽电机的气隙磁场分布进行了理论分析，得出气隙磁场轴向和径向磁场分布的解析结果。黄克峰等[10]针对轴向充磁圆筒型永磁直线电机的磁场分布和气隙磁场的计算与径向充磁问题，提出了一种基于基本气隙磁场计算轴向充磁圆筒型永磁直线电机磁场的解析计算法。

本文对动磁式直线发电机其磁路结构进行了研究，设计了一种直线发电机磁路结构，采用Ansys/Maxwell 建立了动磁式直线发电机的电磁场仿真模型，模拟得到了直线发电机空载运行时的磁感线分布和磁感应强度分布，并计算了直线发电机的空载感应电动势。

1 模拟过程

动磁式直线发电机主要包括：动力活塞、托架、永磁体、绕组线圈、发电机初级（即外轭铁）和发电机次级（即内轭铁）等，如图1 所示。永磁体贴在托架上，并与动力活塞固定，共同组成直线发电机的运动部件。工作时，直线发电机初级和次级静止不动，动力活塞带动直线发电机的运动部件往复运动，从而实现机械能向电能的转化。以动力活塞为纽带，自由活塞斯特林发动机和直线发电机相耦合，最终实现热能-机械能-电能的转化。

图 1 直线发电机示意图Fig.1 Schematic diagram of linear generator

采用Ansys/Maxwell 进行模拟，Ansys/Maxwell是基于有限元法的电磁场分析软件。所谓有限元法，即将整个区域划分成很多很小的子区域，这些子区域一般叫做“单元”或“有限元”，把求解边界问题的原理应用到这些子区域中，求解每个子区域，再把各个子区域的结果综合起来以得到整个区域的解[11]。

1.1 结构参数

本文所研究的直线发电机的磁路结构为：初级结构采用半闭口平行单槽结构；次级结构采用传统的圆环式结构；发电机动子由永磁体和两个辅助极组成，永磁体和辅助极无间隙；永磁体采用径向冲磁方式。具体结构参数见表1。在永磁体两端增加辅助极，采用齿尖向内的初级形状有助于提高绕组磁链和感应电动势。

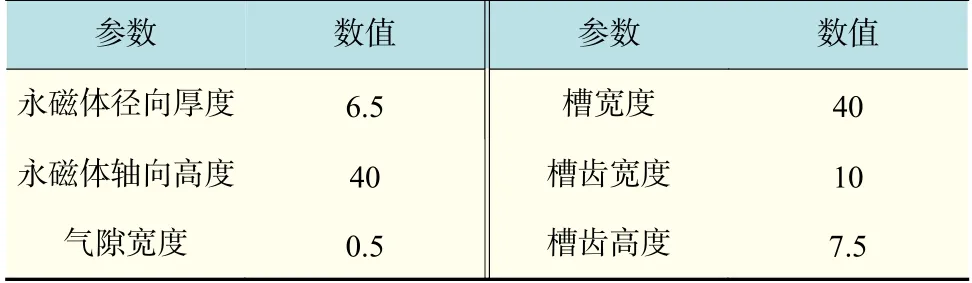
表 1 动磁式直线电机结构参数Tab.1 Structural parameters of moving magnet linear motor mm

1.2 电磁场仿真模型

动磁式直线发电机的二维模型如图2 所示。整个外部区域均为求解区域，Band 域的作用是将模型中运动部分和静止部分分开，Band 域内为运动部分。外轭铁即初级，内轭铁即次级。

图 2 发电机二维模型Fig.2 2D model of the generator

1.3 有限元计算

Ansys/Maxwell 有限元求解步骤为：首先确定电磁场求解器，本模型是在Transient 场求解器下建立的。其次确定几何模型坐标系，根据直线发电机的几何结构，选择Cylindrical about Z 坐标系，即关于Z 轴旋转对称。之后定义电机结构的材料，气隙及直线发电机周围为空气，相对磁导率μr=1。初级、次级和辅助极用50W470 硅钢片。线圈绕组材料为铜。永磁体材料为NdFe35，相对磁导率μr=1.099 8，剩磁为1.23 T，矫顽力为890 kA/m。最后设定相应边界条件，划分网格，由Maxwell方程组[12]和有关控制方程进行求解。

在有限元求解中，永磁体工作点位于回复线上，回复线是一直线。当永磁体回复线和退磁线重合时，永磁体工作点的磁感应强度B 和磁场强度H 关系为

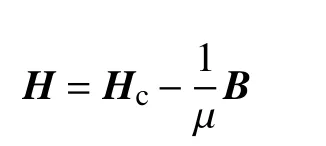
式中：Hc为计算矫顽力；μ 为磁导率，μ=μ0μr，μ0为真空磁导率。

以矢量磁位A 作为求解函数，根据Maxwell方程，直线发电机电磁场的边值问题可描述为

式中：Js为电流源区电流密度；Ω1 为非永磁区域；Ω2 为永磁区域。

此边值问题的等价变分问题转化为求F（A）的最小值，其表达式为

在二维场中，矢量A，Js只有轴向分量。Hc可表示为

式中，θ 为磁化方向和x 轴的夹角。这就得到了关于永磁体的控制方程。

Maxwell 方程的微分形式表示为

式中，v 为运动物体的速度。

采用瞬态求解时，直线发电机模型一部分固定，这部分速度为零。运动部分处于自身坐标系，偏时间导数转变为矢量磁位A 的全时间导数，所以运动方程变为

求解上述方程就可获得直线发电机运动中任意时刻任意一点的矢量磁位，进而可推导电磁场中其他的场量。

2 空载磁场分布

直线发电机在空载运行时，发电机的线圈绕组开路，发电机处于空载状态。自由活塞斯特林发动机驱动直线发电机动子作往复直线运动，永磁体产生的磁场与直线发电机线圈绕组之间有相对运动，所以直线发电机的线圈绕组中会产生感应电动势，但无法形成电流，故没有电流对永磁体产生主磁场的影响，即直线发电机的磁场完全由永磁体提供。

永磁体产生的空载磁场强度和永磁体运动中的磁场分布规律对直线发电机空载感应电动势影响极大。因此，准确计算直线发电机的参数和性能首先要得到直线发电机的磁场分布。

2.1 磁感线分布

图 3 磁感线分布Fig.3 Distributions of magnetic induction lines

图3 所示为发电机动子运动时不同时刻t 永磁体产生的磁感线分布。从图3 可以看出，0 s 时，动子处于初始平衡位置，磁感线主要集中在齿尖处，轭部和齿部基本没有磁感线，此时主磁通基本为零；0.005 s 时，动子处于位移正向最大位置，主磁通达到最大，存在少量漏磁；0.01 s 时，动子回到平衡位置，这是磁感线分布与初始时刻基本相同；0.015 s 时，动子处于位移负向最大位置，磁感线分布与0.005 s 时磁感线分布相似，同样存在少量漏磁。

2.2 磁感应强度分布

图4 所示为直线发电机动子运动时不同时刻t 的磁感应强度分布云图，红色代表磁感应强度最大，蓝色代表最小，其他颜色代表处在最大值与最小值之间。从图4 可以看出，当动子处于平衡位置时，初级齿尖磁感应强度较大，而初级齿部和轭部磁感应强度较小；当直线发电机动子运动到位移正、负向最大位置时，初级齿尖的磁感应强度同样较大，所以在进行磁感应强度分析时要重点关注初级齿尖的磁感应强度大小。

图 4 磁感应强度分布Fig.4 Distributions of magnetic induction intensity

3 空载感应电动势计算

准确计算出直线发电机的空载感应电动势是有助于对其进行性能分析和深入优化设计的。本文采用Ansys/Maxwell 模拟计算直线发电机的空载感应电动势。通过对直线发电机的有限元分析，可利用法拉第电磁感应定律来计算直线发电机空载感应电动势。

式中：Ψ 为总磁链；t 为时间。

首先，需要获得动子在不同位置时定子绕组线圈中的磁链分布。动子速度为自由活塞斯特林发动机热力学和动力学设计给出，速度2.513 cos(100 πt)，m/s，其中：f 为频率；X 为振幅8 mm；t 为时间。

直线发电机动子运动到不同位置时，永磁体发出的磁通经过直线发电机的永磁体、气隙、初级、辅助极和次级等匝链绕组线圈形成回路。对匝链绕组线圈截面的磁链进行积分求和，便可以得到绕组线圈中总磁链与时间的关系。再对总磁链进行求导便可得到直线发电机绕组线圈中产生的空载感应电动势。直线发电机磁链和感应电动势的一个周期变化如图5 所示。从图5 可以看出，直线发电机空载感应电动势呈现正弦变化趋势，在波峰波谷未发生明显畸变。

图 5 磁链和感应电动势随时间变化图Fig.5 Flux and induced electromotive force vs. time

空载感应电动势的有效值U 表征了直线发电机输出电压的能力，可表示为

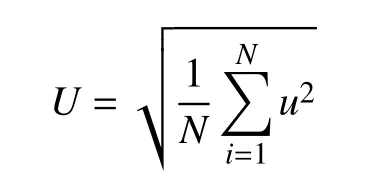
式中：N 为一个周期的取点个数，N 值越大，有效值计算越精确；u 为空载感应电动势瞬时值。

根据上式可求得空载感应电动势的有效值U 为111.22 V。

4 总 结

针对自由活塞斯特林发电机中的动磁式直线发电机，设计了一种磁路结构，即在永磁体两端增加辅助极，采用齿尖向内的初级形状，这种磁路结构减小了漏磁，有助于提高绕组磁链和感应电动势。建立了此磁路的动磁式直线发电机电磁场仿真模型，采用Ansys/Maxwell 进行数值模拟，得到了空载运行时不同位置的磁感线分布和磁感应强度分布云图，发现不论动子运行到任何位置，齿尖位置的磁感应强度总是最大，所以在进行磁感应强度分析时要重点关注初级齿尖的磁感应强度大小。