分块对称r 循环算子的范数不等式

史一彬， 秦 梅

（上海理工大学 理学院，上海 200093）

基于降阶的思想，由分块循环算子的元素估计分块循环算子范数的方法近年来越来越引起研究者的关注。Audenaert[1]给出了形如A=的半正定 2×2块矩阵的范数上下界，Bani-Ahmad 等[2]研究了一般形式的 2 ×2块算子的范数不等式，潘雪等[3]、史雨梅等[4]研究了首尾差r-循环矩阵和块结构首尾差r-循环矩阵的对角化和范数估计，Bani-Domia 等[5]给出了无参数的分块循环算子的范数估计结果，文献[6]研究了带复参数的分块循环算子的范数等式和不等式。本文也在此基础上给出了分块对称 r循环算子和分块对称 r反循环算子的范数等式与不等式结果。

1 预备知识

令B(H)为n维复可分Hilbert 空间 H上的所有有界线性算子的 C∗-代数，n个H空间的直和记作若是B(H)中的算子，则分块算子可视为中的算子，且对任意分块向量x=(x0,x1,···,xn−1)T∈H(n)有

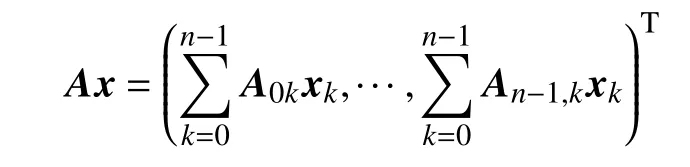
若A0,A1,···,An−1是 B(H)中的算子，则分块对称 r循环算子记为

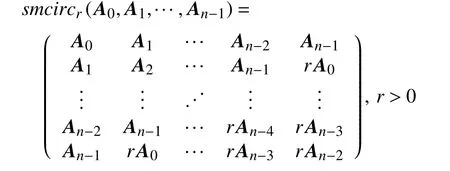
分块对称 r反循环算子记为

称定义在 B(H) 中 的范数 τ为弱酉不变范数[8]，如果对于任意的 A ∈B(H)， 同阶酉算子 U ∈B(H)满足τ(A)=τ(UAU∗)；称定义在算子理想（包含在紧算子理想中）中的范数 | ||·|||为酉不变范数[8]，如果对于 任 意 的 A ∈B(H)及 同 阶 酉 算 子 U,V ∈B(H)满 足

算 子 A ∈B(H)的 Schatten p−范 数[9]记为‖A‖p=其中p ∈[1,+∞) ； σj(A)(j=1,2,···,n)为 A的奇异值，且易知 ‖·‖p是酉不变的。

2 分块对称r 循环算子的范数上界

定理1若 A0,A1,···,An−1∈B(H)且 r ≠1，则有

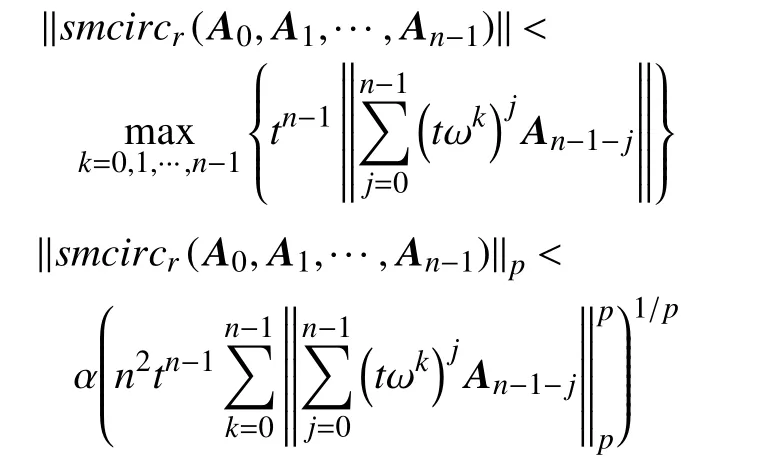
证明令1,ω,ω2,···,ωn−1为n个单位根，ω=e2πi/n，

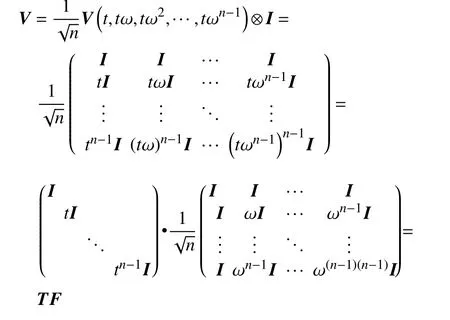
这里及下文中 ⊗表示Kronecker 积。

smcircr(A0,A1,···,An−1)有如下形式的准对角化结果

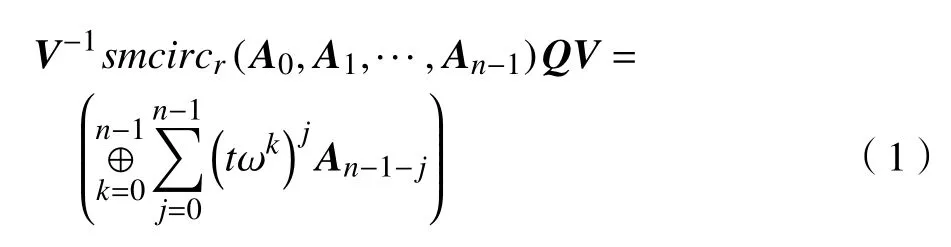
这里

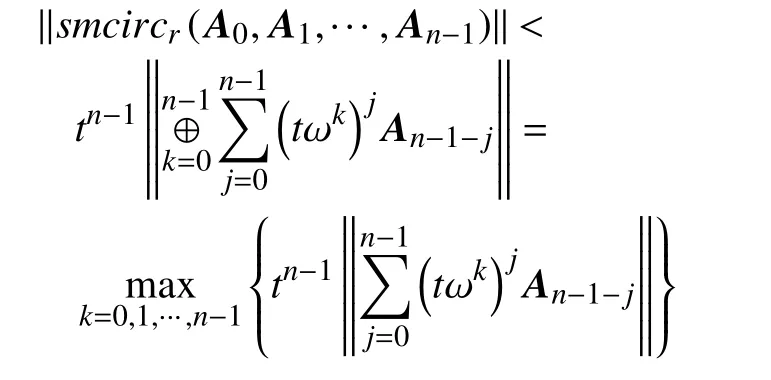
同理，由式（1）可得

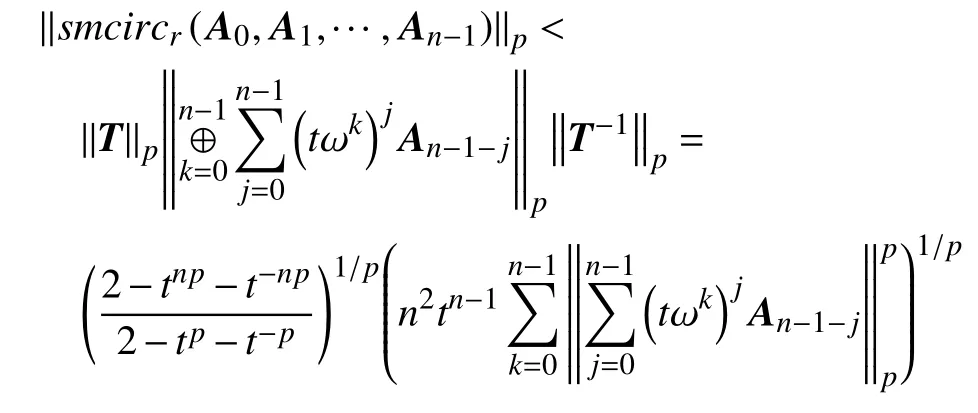
推论1若 A0,A1,···,An−1∈B(H)， r =1则有

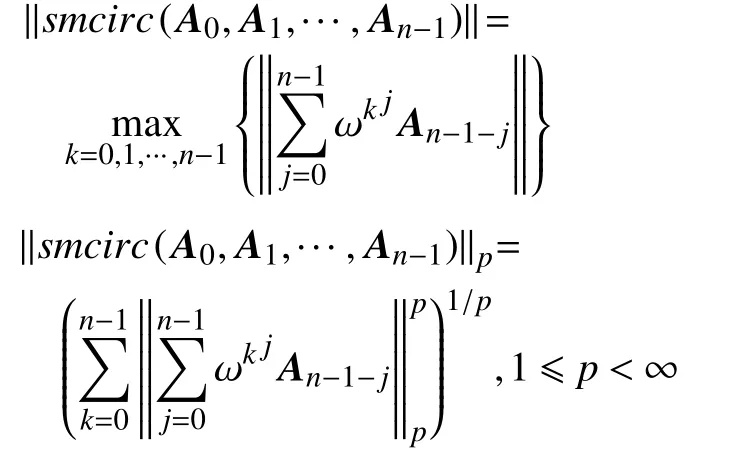
特别地，当 n =2时，有

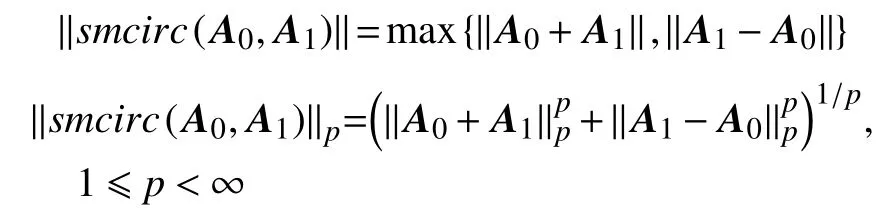
推论2若 A,B ∈B(H)， r ≠1，则

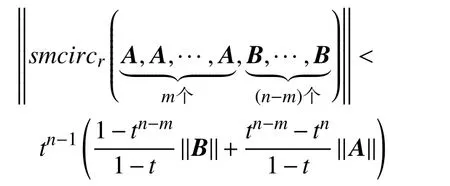
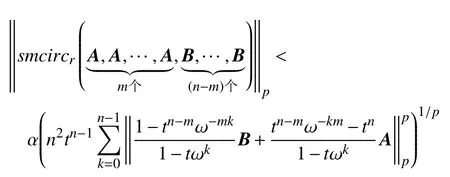
特别地，当 m =n时，

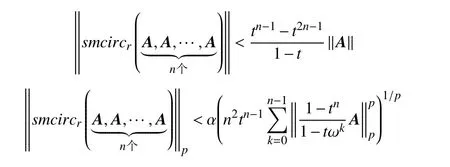
证明由定理1 知

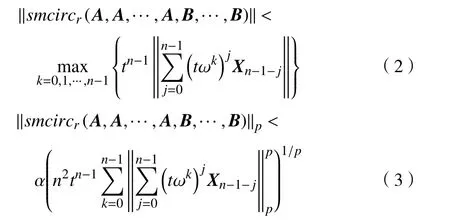
这里 X= A 或 B。

对于某个k，式（2）右边

3 分块对称r 反循环算子的范数上界

定理2若 A0,A1,···,An−1∈B(H)且 r ≠1，则有

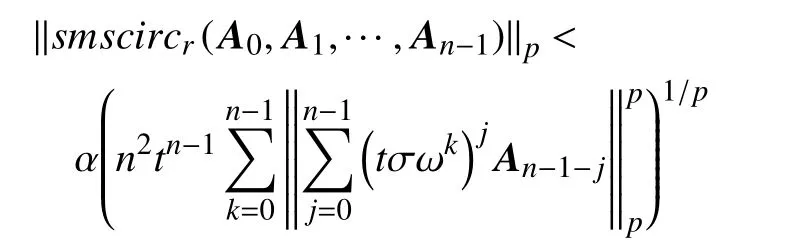
证明令方程zn=−r 的n 个 根为tσ,tσω,tσω2,···,

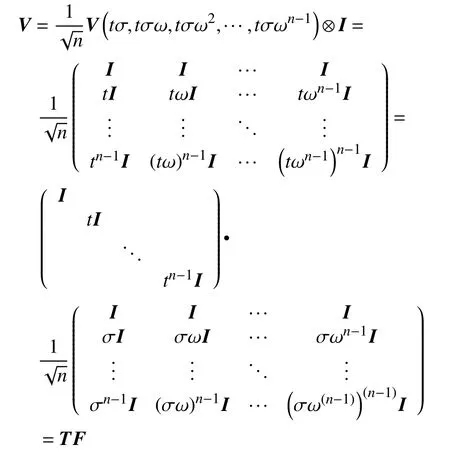
所以 V−1=F∗T−1. 又 smscircr(A0,A1,···,An−1)有如下形式的准对角化结果：

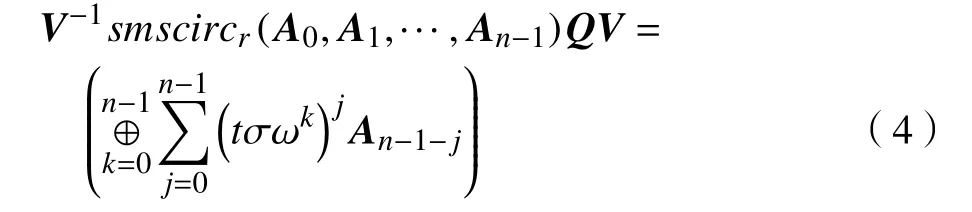
这里 Q与式（1）中相同。

由定理1 的证明易知

同理，由式（4）可得

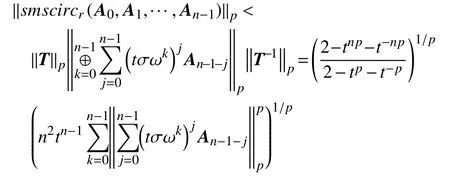
推论3若 A0,A1,···,An−1∈B(H)， r =1，则有

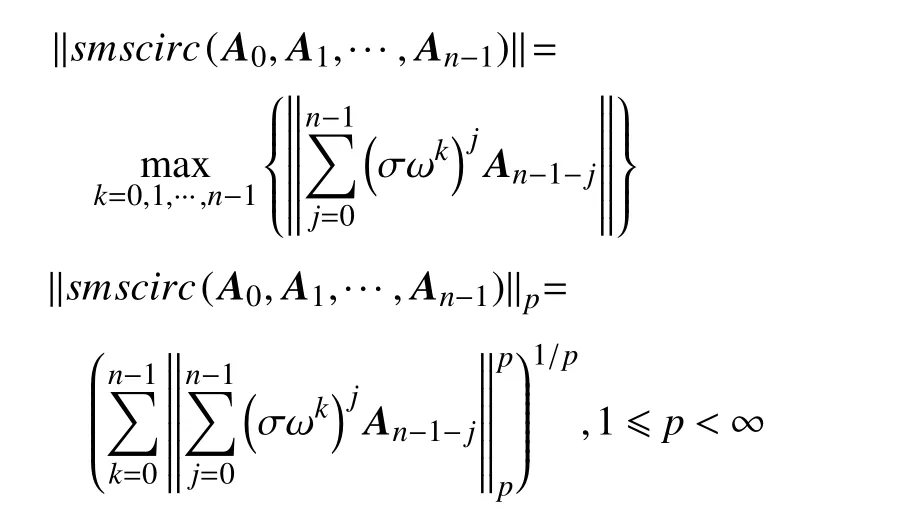
特别地，当 n =2时，有

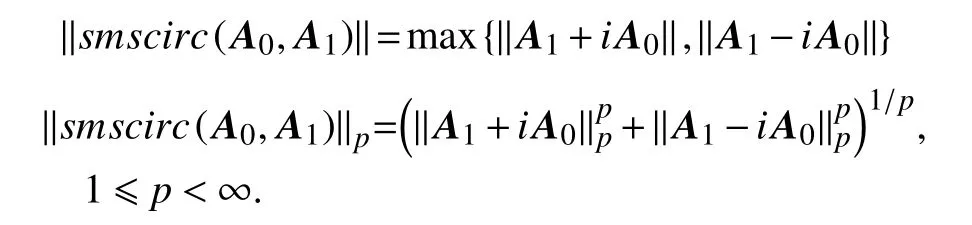
推论4若 A,B ∈B(H)， r ≠1，则

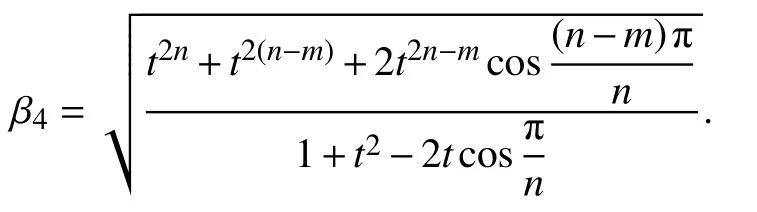
特别地，当 m =n时，

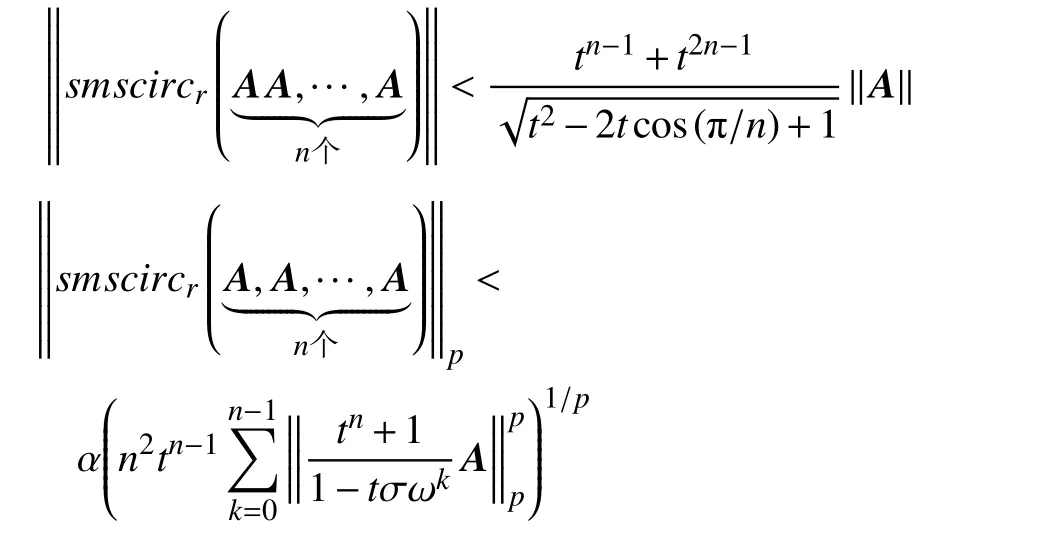
证明由定理2 知

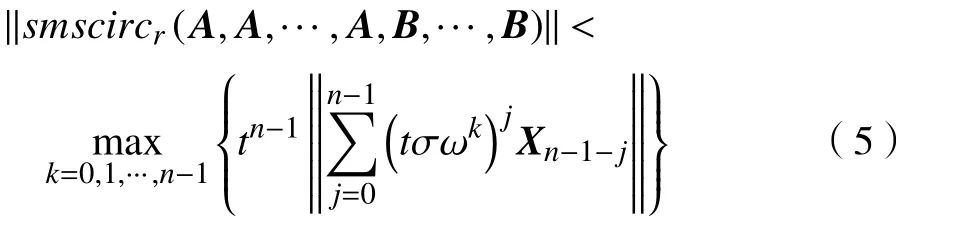
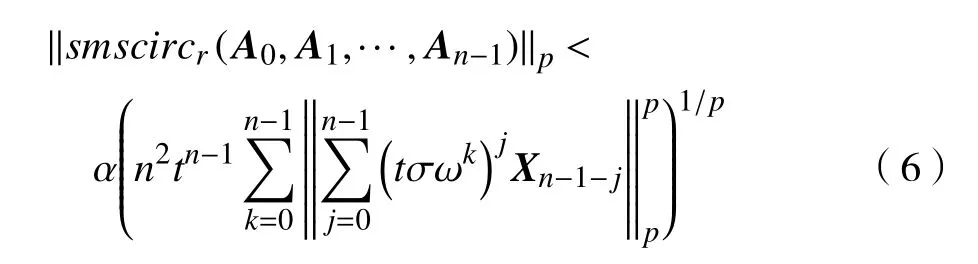
这里 X= A 或 B。

对于某个k，式（5）右边

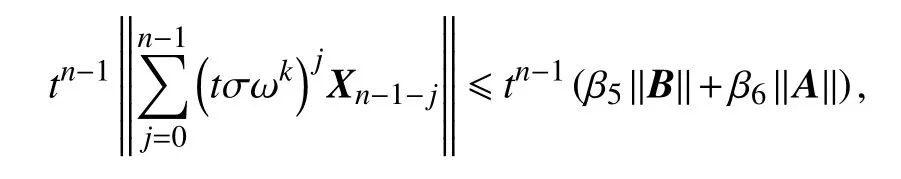
这里

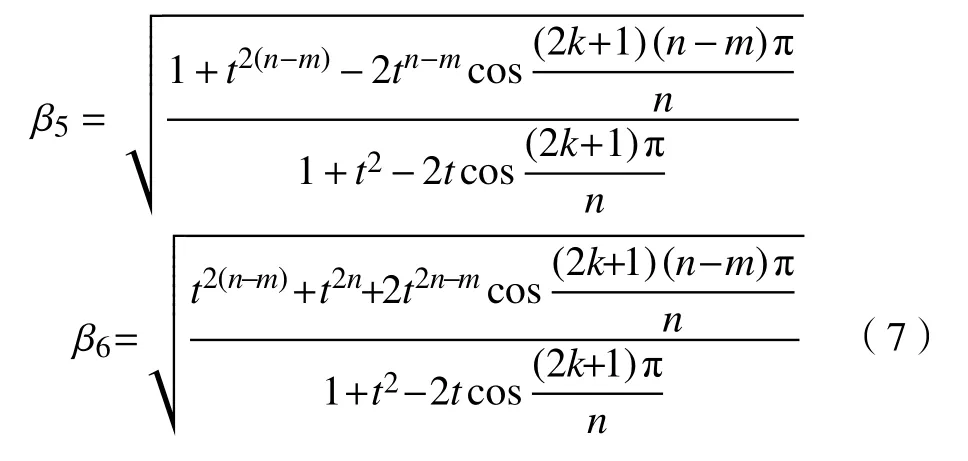
且当 k =0时，取得最大值为

式（6）右边合并后即得证。

4 结 论

上述的系列结论给出了分块对称r 循环算子和分块对称r 反循环算子降阶的范数结果（r =1）或范数上界结果（ r ≠1）， 在一定程度上降低了计算和估计分块对称r 循环算子和分块对称r 反循环算子范数的复杂度。 对于分块对称r 循环算子和分块对称r 反循环算子上界的更好的估计及其下界结果还有待进一步研究。