多时间尺度需求侧响应模型及其电价定价策略
周 丹1,戴慧雯1,陆海清,楼伯良,黄弘扬
(1.浙江工业大学 信息工程学院,浙江 杭州 310023;2.国网浙江省电力公司 电力科学研究院,浙江 杭州 310014)
为了解决当前电力系统中出现的电力供给和需求不匹配、负荷高峰[1]等问题,进一步优化电力系统结构和运行方式,满足人们对更优质电力供应的迫切需求,我国开展了新一轮的电力改革。新电改9号文提出了“管住中间,放开两头”的电力运营模式,通过在售电侧引入竞争机制,使得电价能够反映成本与供求关系[2],在政策和机制上使得需求侧响应有了更好的实施空间,从而能更好地解决电力系统中出现的问题。然而现有的电力系统规划、运行模式存在诸多问题:1) 用电尖峰时刻短暂的巨大需求量造成了大量资源浪费;2) 当政府设置的最高价格已经低于边际供应成本的时候,人们不会去节约资源;3) 风电、光伏、潮汐、生物质能等分布式电源[3]接入电网,由于其自身的波动性、随机性、间歇性,并网后会增大峰谷差,降低输送电能的效率,电能的质量也会受到影响。而需求侧响应,通过政策措施和经济激励来引导用户在用电高峰时期少用电、低谷时期多用电,可以提高用电效率、优化用电方式,可以缓解缺电压力、降低供电成本,还有助于电力用户更多地参与电力市场,并积极地促进整个电力系统的节能减排,促进分布式能源的发展,能产生一定的环境效益。如果合理运用需求侧响应,可以解决上述提出的诸多问题。
目前国内外已经有许多文献对需求侧响应做了相关研究。峰谷分时[4-5]由于良好的削峰填谷作用,对于需求侧响应有积极的影响,在国内外电力工业经济管理中起着重要作用。文献[6-7]建立了基于分时电价的需求弹性数学模型,使得电力用户在分时电价下的用电量根据电力需求价格弹性得到一定反映,但缺少对电价的预测。文献[8-13]在考虑需求弹性数学建模的基础上同时考虑了需求侧响应建模中诸如用户满意度、心理、决策机制、企业受益、市场原理以及时滞性等因素的影响。谭忠富等[8]建立了考虑用户满意度的需求弹性数学模型;阮文骏等[9]基于消费者心理学原理,参考一般用户反应模型,建立了用户对分时电价的反应模型;谈金晶等[10]反映多方决策对分时电价的影响,建立了含供电、用户和政府部门的智能体系统,研究了他们之间的相互影响;陈沧杨等[11]建立了以目标函数为电网经营企业收益最大化的峰谷分时电价模型;Celebie等[12]基于市场均衡原理,研究了不同边际成本定价规则下用户对电价的响应行为;姚珺玉等[13]提出了电价响应时滞性的概念与数学模型。但是现有文献只考虑了短期需求侧响应的建模方法,这些模型无法反应中长期时间尺度的需求侧响应特性。为了更好地描述电力需求侧响应的运行机理,有必要建立综合反应短期和中长期需求侧响应特性的多时间尺度需求侧响应模型。因此,笔者提出了新电改背景下综合考虑短期电力需求特性和中长期电力需求特性的多时间尺度需求侧响应建模方法及其分时电价定价策略。该建模方法在基于分时电价的需求弹性量化模型的基础上,分析现有中长期电价模型之后,结合新电改中需求侧响应的新特点[14],通过在需求侧响应模型中同时考虑短期电价和中长期电价对需求侧响应的影响,提出多时间尺度需求侧响应模型,能够反应出中长期电价波动情况下的短期电力需求特性;然后以执行峰谷分时电价后峰谷负荷差值占负荷总量最小为目标函数,选择了粒子群算法作为优化算法;最后以IEEE-30节点的配电网进行算例分析,来验证所建基于峰谷差优化的多时间尺度需求侧响应模型的有效性。
1 多时间尺度需求侧响应建模
1.1 电力需求特性分析
1.1.1 中长期电力需求特性分析
中长期电力需求特性往往与城市化率、工业化率、国内生产总值、电力使用效率、电价水平、家用电器数量等有关。中长期需求模型根据研究目标不同分为多种,由于本研究以居民用电需求为研究对象,选择中长期电力需求模型的函数表达式,即
Inq=α1Iny+α2Inp+α3InS+ε
(1)
式中:α1,α2,α3都是估计系数,需要通过对实际数据的处理得出;y表示人均可支配收入,元/年;p表示长期电价,元/kWh;S表示人均居民住宅面积,m2/人;ε表示随机误差;q表示年均电力需求量,kWh/年。
郁义鸿等[15]分别用最小二乘法(OLS)和自回归分布滞后模型(ARDL)来得到估计系数,结果发现自回归分布滞后模型得到的结果要更优,笔者根据参考文献中的数据,进行了修正,即
Inq=0.601Iny-8Inp+0.877InS+2 000
(2)
1.1.2 短期电力需求特性分析
短期电量电价的模型主要是根据消费者心理学[9]建立的,采用分时电价作为短期电力需求研究对象,通过已有的电力需求调查数据,可以将用户的短期需求模型拟合成分段线性函数,即
(3)
式中:λij表示j时段向i时段转移的电量;Δpij表示j时段与i时段的电价差;K表示用户反应度模型的斜率;A表示死区阈值;B表示饱和区阈值。
本研究将式(3)中的Δpij修改为Δpj/p,原来的表达式Δp代表两个不同时段的电价之差,新的表达式中,Δpj表示的是pj-p,其中pj表示j时段的电价;p表示常量,指代的是电价。这样表达式所代表的就是电价变化率与电量变化率之间的关系,这样做的好处是可以表示出各时段的自弹性,使得短期电价模型更完整。λij表示j时段的电价变化后,引起了i时段电量的变化,即i时段电量变化率,得到的函数为
(4)
分时电价是指根据系统负荷水平,将每天划分为峰、平、谷等多个时段,每时段执行不同电费标准的电价制度。本研究为了简化模型,将分时电价分为峰、平、谷3个时段,用f,p,g来表示。
通过对用户历史用电量数据的分析处理,采用最小二乘法[9]拟合曲线的死区阈值、饱和区阈值以及用户反应度模型的斜率,由此得到图1峰价和峰用电量变化率关系的曲线。横坐标表示峰价变化率;纵坐标表示峰用电量变化率;点(0.05,0)为分段线型峰价、峰用电量变化率关系曲线的死区拐点,0.05为死区阈值;点(0.4,0.14)为分段线型峰价、峰用电量变化率关系曲线的饱和区拐点,0.4为饱和区阈值,0.14为峰时段电价引起峰时段用电量的最大用电量变化率;峰价和峰用电量变化率关系曲线的斜率即表示用户反应度模型的斜率。由此得到短期电量电价模型为
(5)
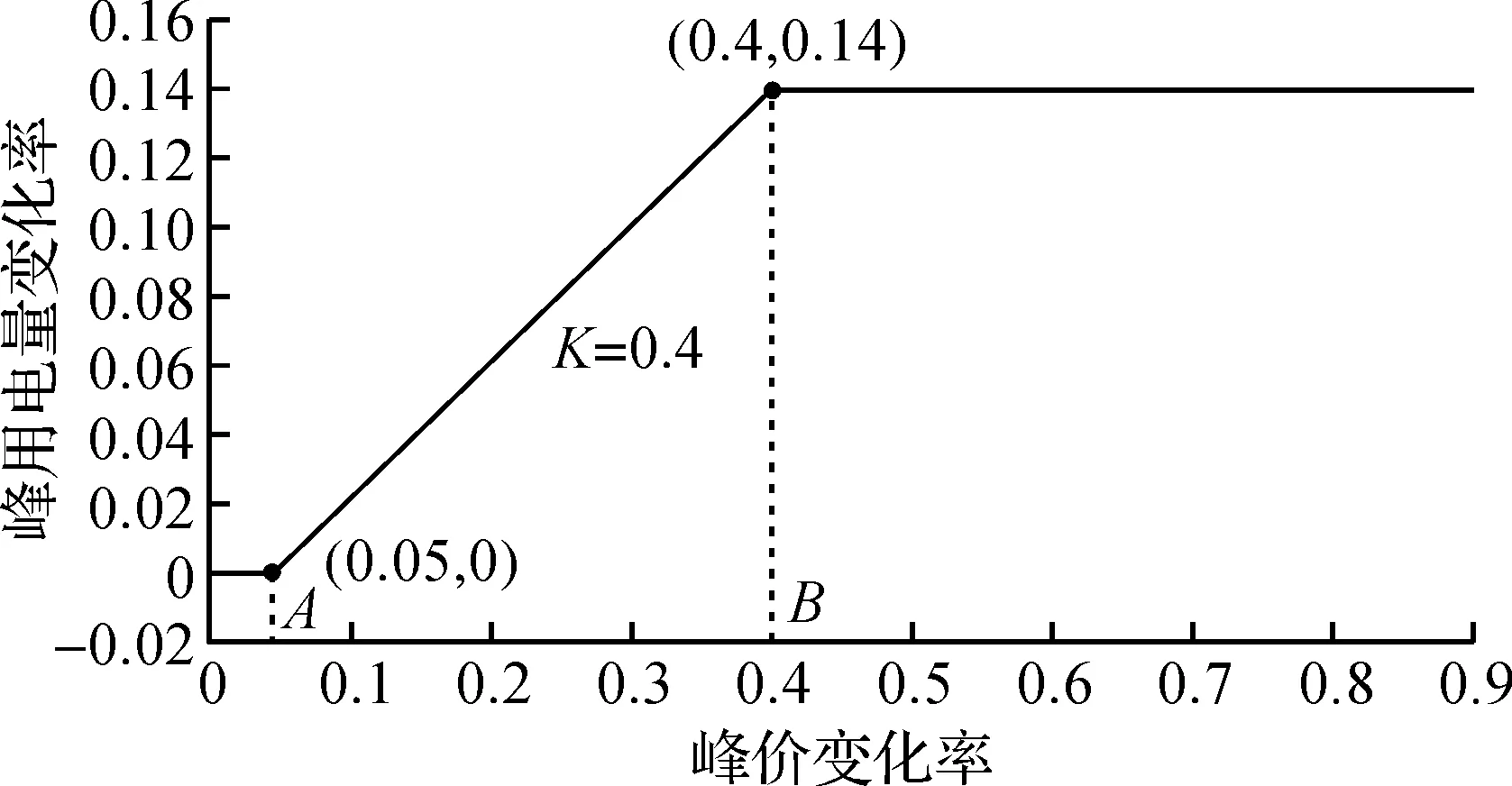
图1 峰价、峰用电量变化率关系曲线Fig.1 Curve of peak price and peak electricity consumption rate change
同理,根据消费者心理学拟合的曲线,将用户反应度模型的斜率、死区阈值及饱和区阈值代入式(4),得到8 个短期电量电价模型,中国城市居民用电的一般价格为0.52~0.62 元,式中的p暂时都取值为0.584 元。8 个短期电量电价模型分别为
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
式(5~13)中基础电价p在短期电力需求特性分析中为常量,但是根据式(2)可以知道基础电价p和基础需求q相互之间有关联,且从中长期时间尺度上来看基础电价p和基础需求q均为动态变化的。因此,简单的用式(5~13)来表示需求响应特性在一些混合了多种时间尺度的应用场景中显然是不够准确的。
1.2 多时间尺度需求侧响应模型
多时间尺度需求侧响应模型构建整体结构如图2所示。
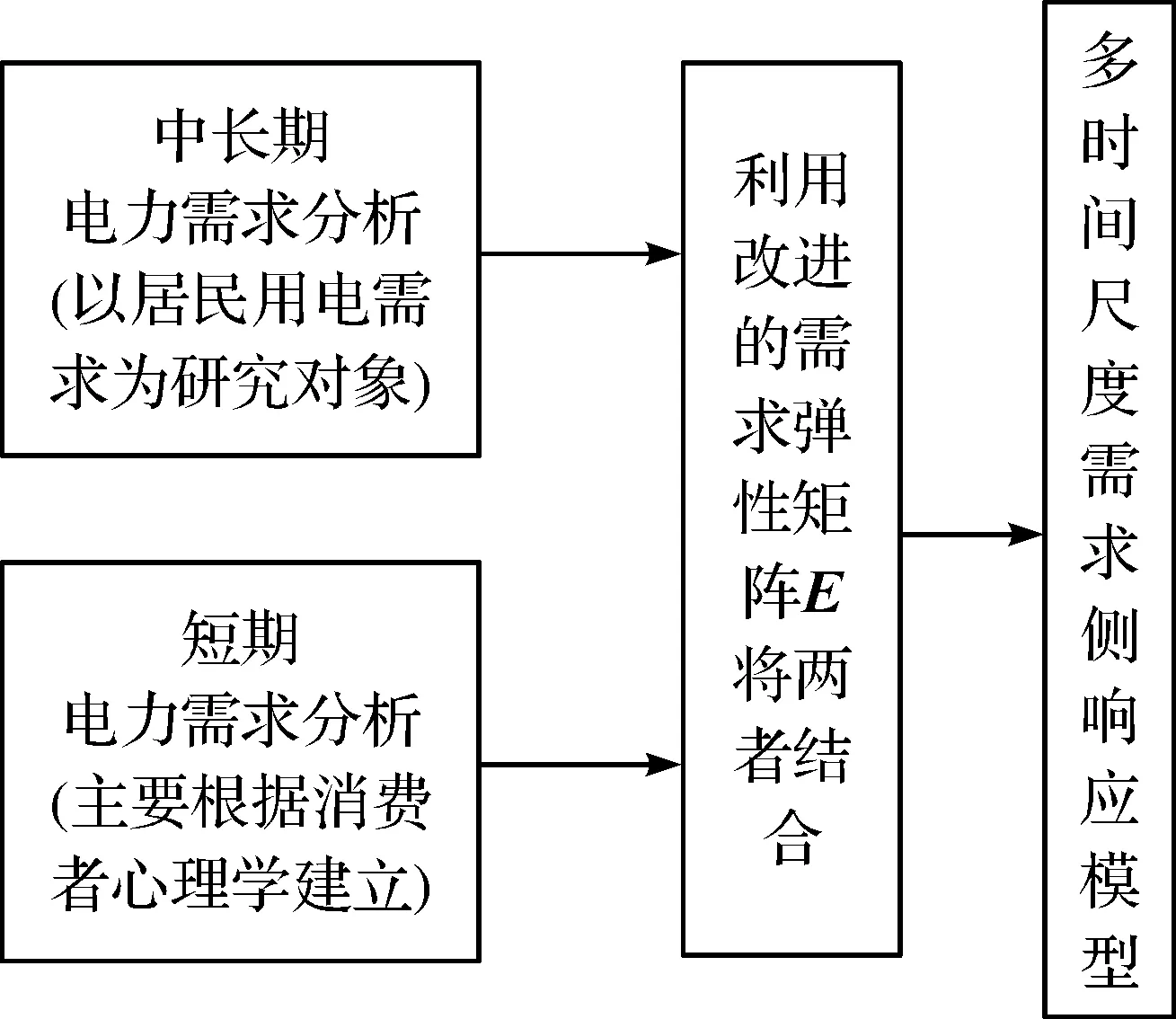
图2 模型结构Fig.2 Model structure
本研究多时间尺度需求侧响应模型是基于需求弹性的量化模型建立的,并且考虑峰、平、谷分时电价。该模型通过需求弹性矩阵将短期电力需求特性与中长期电力需求特性结合起来,形成多时间尺度需求侧响应模型。
需求弹性模型就是由电量电价弹性矩阵构成的。电力需求的价格弹性可以认为是需求量的变化率与价格的变化率之比。需求弹性的量化模型可以用需求弹性系数来表示,即
(14)
式中:εij即需求弹性系数;Δqi/qi表示i时段的需求量变化率;Δpj/pj表示j时段的电价变化率。
根据需求弹性系数,将一天分为n个时段,则可以得到如下n×n阶电量电价弹性矩阵
(15)
式中:对角线元素为自弹性系数;其余元素为互弹性系数。
多时间尺度需求侧响应模型是根据式(14)推导所得,其函数表达式为
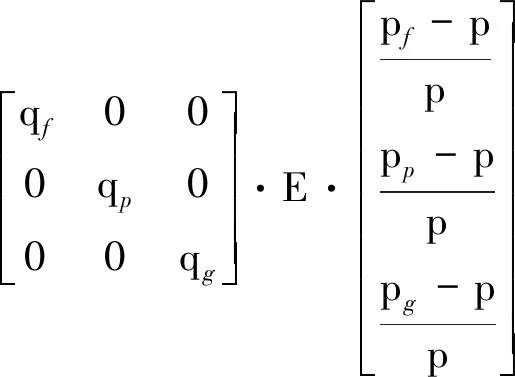
(16)

式中改进的需求弹性矩阵E是将式(5~13)的λij(i=f,p,g;j=f,p,g)代入式(14)中替代Δqi/qi。由峰、平、谷电价pf,pp,pg,以及长期电价p,结合式(5~13)就可以得到9 个εij(i=f,p,g;j=f,p,g)的值,将这9 个值代入式(15)中,就可以得到
(17)
式中:对角线上的值表示峰、平、谷3个时段电量电价的自弹性系数;其他6 个值表示峰、平、谷时段之间的电量电价互弹性系数。
2 电价定价策略
2.1 目标函数
目标函数设置为执行峰谷分时电价后峰谷负荷差值占负荷总量最小,这是研究分时电价问题时最常见的设置方法,也是最直接的目标函数。通过实施需求侧响应降低峰谷差[6],就可以实现提高电网稳定性、降低资源投入、减少支出的目的。目标函数的表达式为
min(qf-DR-qg-DR)/(qf-DR+qp-DR+qg-DR)
(18)
式中qf-DR,qp-DR,qg-DR分别代表实施需求侧响应后的峰、平、谷时段用电量。
2.2 约束条件
为了防止峰、平、谷电价倒置,同时也为了防止峰时段电价低于长期电价,谷时段电价高于长期电价,平时段电价没有特殊要求。对价格的约束为
(19)
价格过低会导致用电浪费,价格过高会限制用户用电的正常需求,因此在价格优化前对峰、平、谷电价设置的区间为
(20)
为了防止峰、平、谷3个时段之间需求量倒置。对需求量的约束为
(21)
分时电价实施后,用户支出的电费要小于分时电价实施前支出的电费,以确保用户可以受益,即
qf-DR×pf+qp-DR×pp+
qg-DR×pg≤q×p
(22)
2.3 求解算法
优化模型求解算法种类众多[16-20],粒子群算法由于其收敛速度快,需要调整的参数较少,易于求解非线性问题得到广泛应用,因此笔者选择了粒子群算法[21-23]作为优化模型的求解算法。具体求解流程如图3所示。
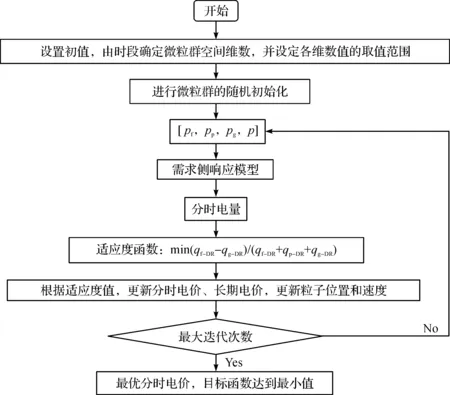
图3 电价定价策略优化流程图Fig.3 Flow chart of price pricing strategy optimization
粒子群算法公式为
v=w·v+c1·rand·(pbest-present)+
c2·rand·(gbest-present)
(23)
present=present+v
(24)
式中:w表示惯性权重;v表示粒子的速度;present表示粒子当前的位置即当前的解;pbest表示单个粒子最优的解;gbest表示整个粒子群中所有粒子在历代搜索过程中所达到的最优解即全局极值;rand表示在[0,1]区间的两个随机数;c1,c2是学习因子,一般为0~4,并且c1=c2。
3 算例分析
为了验证笔者建立的多时间尺度需求侧响应模型及其电价定价策略的有效性和实用性,以IEEE-30系统为例进行算例分析;运用matlab对上述理论模型进行仿真计算,将该需求侧响应模型实施多时间尺度需求侧响应前后的情况对比。
3.1 参数设置
仿真中用到的峰、平、谷时段初始用电量是根据一天中的人均总用电量来划分的,具体参数设置如表1所示。

表1 需求侧响应参数设置Table 1 Requirement side response parameter setting
人均用电量q是通过式(2)长期需求模型的函数表达式计算得出的。
对粒子群算法的参数设置如表2所示。

表2 粒子群算法参数设置Table 2 Particle swarm optimization parameter setting
按照本研究内容的需要,粒子数取常用的40;c1,c2也取了平均值2;最大速度vmax为0.4是根据寻优的范围来确定的;维度D设置为4是因为输入参数优化变量有4 个,分别是峰时段电价、平时段电价、谷时段电价、长期电价;循环次数没有限制,暂时设置为2 000;惯性权重是根据最大速度vmax来确定的,本文中的vmax并不大,因此设置w为1。笔者电价定价策略应用于IEEE-30节点系统,图4是IEEE-30节点配电网结构图。
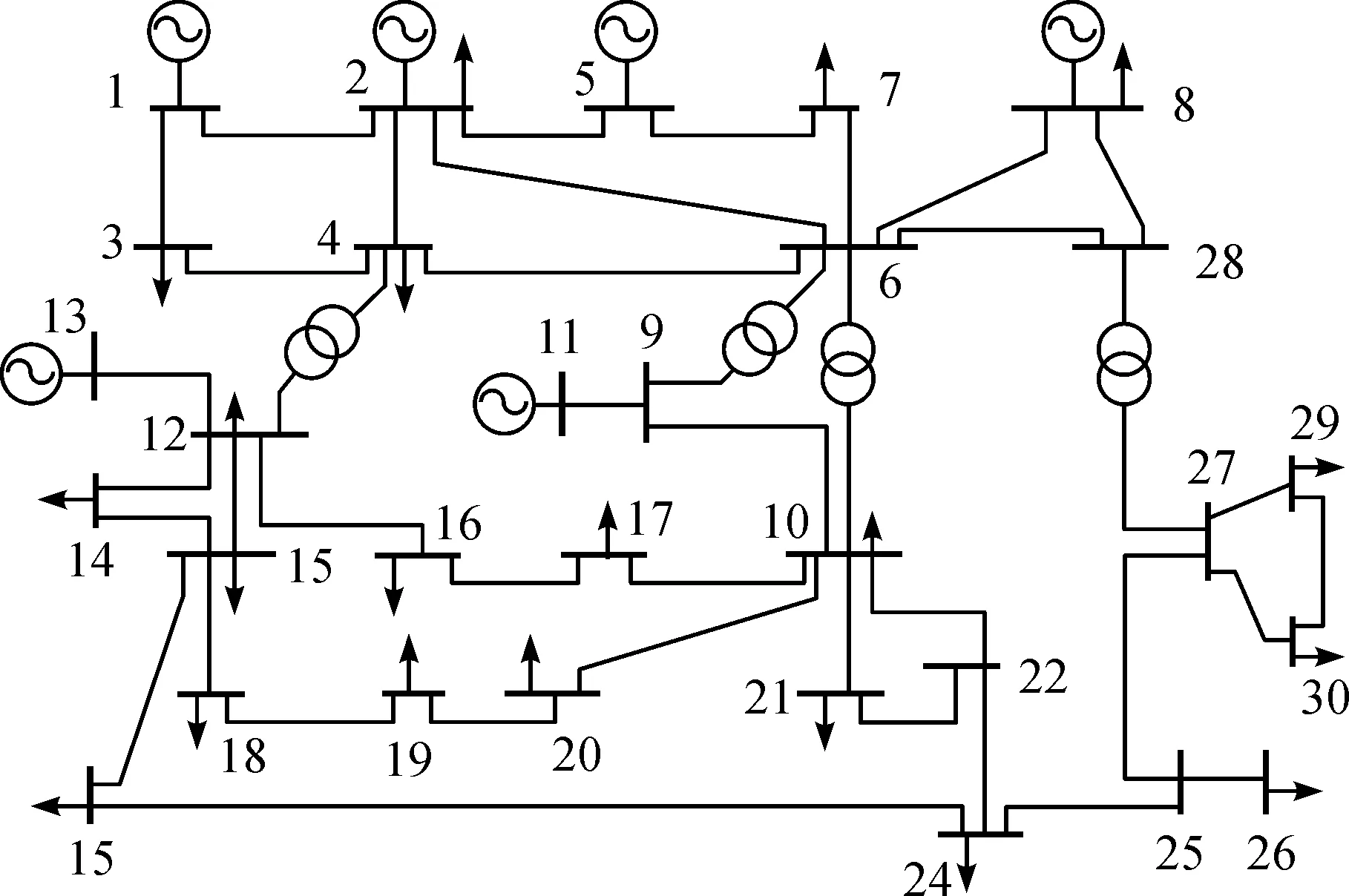
图4 IEEE-30节点配电网结构图Fig.4 IEEE-30 bus distribution network structure
3.2 结果分析
3.2.1 需求弹性矩阵
根据式(5~17)可知本文需求弹性矩阵并不是常量,是与电价耦合在一起求解的变量,对式(18~22)所描述的电价优化模型求解后得到的结果为

从需求弹性矩阵可以看出:对角线表示的自弹性均为负值,且数值较大,峰荷的自弹性偏小。
3.2.2 电 价
采用短期需求侧响应模型求得峰、平、谷分时电价情况如表3所示[9],笔者采用基于峰谷差优化的多时间尺度需求侧响应模型仿真所得分时电价如表4所示。

表3 短期需求侧响应模型优化后的分时电价Table 3 Time-of-use price after short-term demand side response model 单位:元/(kWh)

表4 多时间尺度需求侧响应优化后的分时电价Table 4 Time-of-use price after multiple time scale demand side response 单位:元/(kWh)
对比短期需求侧响应模型,多时间尺度需求侧响应模型优化后的峰时段电价增加了0.102 元,平时段电价增加了0.013 元,谷时段电价减少了0.041 元。将多时间尺度需求侧响应优化后的分时电价与长期电价作比较,以峰谷负荷差值占负荷总量最小为目标进行优化后,峰时段电价提升较多,平时段电价略有上升,谷时段电价下降较多。该结果与预期效果,即“将峰时段电价调高,谷时段电价调低”一致,这样可以引导用户在用电高峰时段少用电、低谷时段多用电,可以提高用电效率、优化用电方式。
3.2.3 优化结果比较
图5~7是以3 种不同方式比较3 种方案的用电量。图5是3 种不同方案关于峰、平、谷用电量的条形图;图6是每时刻3 种不同方案的用电量曲线;图7是3 种不同方案的总用电量和峰谷差用电量条形图。方案1没有使用分时电价,方案2使用短期需求侧响应模型[9],方案3使用多时间尺度需求侧响应模型。
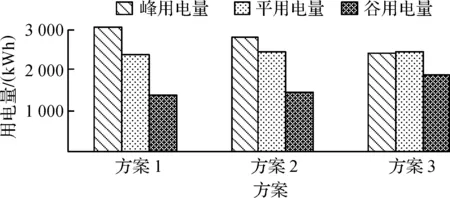
图5 3 种不同方案下峰、平、谷用电量Fig.5 Electricity consumption of peak, flat and valley under three different schemes
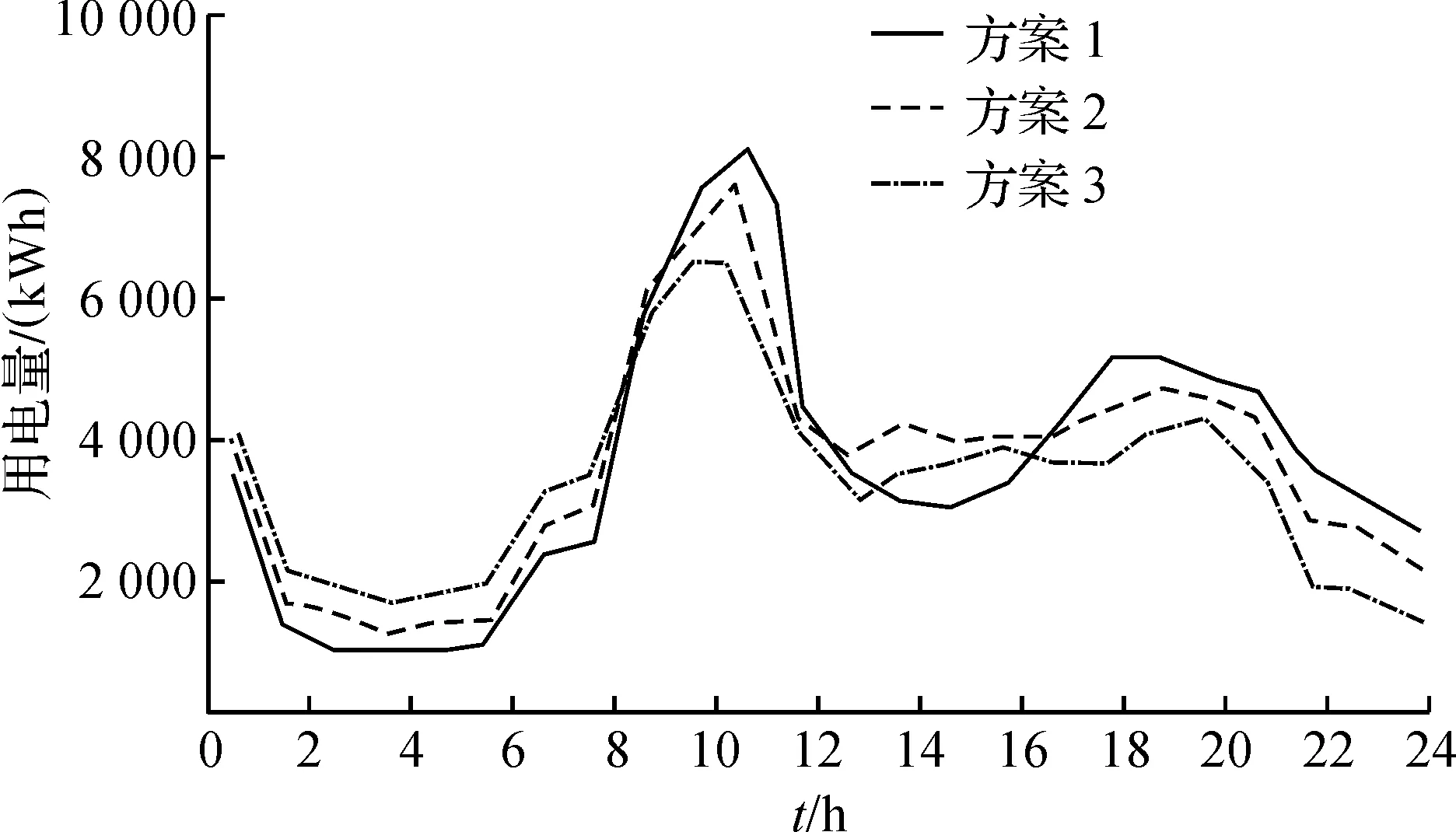
图6 每时刻3 种不同方案的用电量曲线Fig.6 Electricity consumption curves of three different schemes at each point of time
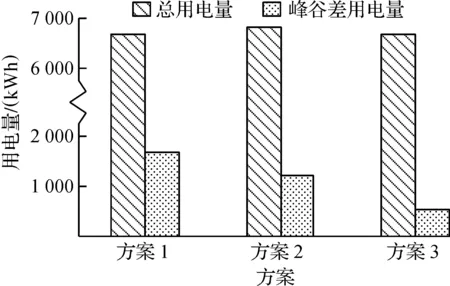
图7 3 种不同方案的用电量条形图Fig.7 Bar charts of electricity consumption for three different schemes
结合图5,6可以看出:在峰时段,方案1的用电量最大;在谷时段,方案3的用电量最大;在平时段,3 种方案的用电量基本相同。从图7可以看出:3 种方案的总功耗基本相同。对短期需求侧响应模型进行仿真后,峰谷差从1 692 kWh优化到1 214 kWh,而对基于峰谷差优化的多时间尺度需求侧响应模型进行仿真后,峰谷差由原先的1 692 kWh优化到521 kWh。结果表明:笔者提出的多时间尺度需求侧响应模型及其电价优化策略能有效地将电量从峰时段转向谷时段。基于峰谷差优化的多时间尺度需求侧响应模型相比于方案2,峰、平、谷电量的变化情况都不大,但峰谷差降低了521 kWh,说明笔者提出的基于峰谷差优化的多时间尺度需求侧响应模型具有良好的削峰填谷作用。
电费方面,方案2对比于方案1平时段电价下降了236 元,谷时段电价下降了296 元,峰时段电价上升了498元。方案3对比于方案1平时段电价下降了214 元,谷时段电价下降了285 元,峰时段电价上升了412 元。结果见表5。
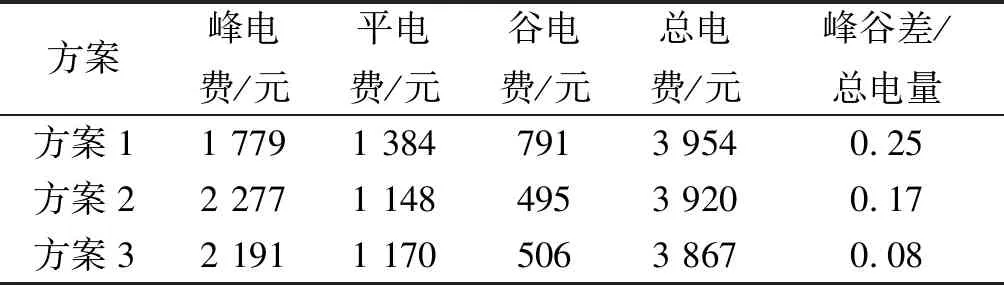
表5 各时段电费情况Table 5 Electricity charges at various times
对比于平时段及谷时段电价的下降,峰时段则上升较多。因此,方案2和方案3通过需求侧响应机制在降低峰谷差的同时没有增加居民的支出,表明笔者提出的多时间尺度需求侧响应模型及其电价优化策略是合理可行的。但从总电费上,方案3略低于方案2,表明笔者提出的多时间尺度需求侧响应模型及其电价优化策略从整体上还是优于短期需求侧响应模型。
4 结 论
针对电价制定问题,建立了多时间尺度需求侧响应模型,提出了电价定价策略,通过仿真分析对电价定价策略进行了验证,仿真结果表明该电价定价策略是有效的。笔者提出的多时间尺度需求侧响应模型为需求侧响应建模提供了一种新思路,为新电改配售电价放开后电价的制定提供了参考。研究过程还存在一些不足,例如,仿真时选取的案例是全国平均值,没有特异性,如果运用到工程实际中,还需要根据当地的统计数据修正模型中的参数。

