改进狼群算法优化的小波常模盲均衡算法
郑亚强
(淮南联合大学 机电系,安徽 淮南 232001)
盲均衡是解决无线通信系统因多径传输形成码间干扰的有效方法之一,可大大节约带宽。常模盲均衡算法(Constant Modulus Algorithm,CMA)简单稳定,使用广泛,但收敛速度慢,稳态误差较大。针对这个问题很多学者提出了相关解决方案,比如用小波变换(Wavelet Transform,WT)降低传输信号的相关性[1],或稀疏化盲均衡器的稀疏均衡器支路的相应抽头[2],又或引入了判决引导算法[3]。这些改进在一定程度上都提升了均衡性能,但在最小化非凸性代价函数过程中仍采用了传统的随机梯度下降法。代价函数取得全局最小值时,均衡器获得初始权向量,初始权向量的质量对最终均衡效果影响显著。随机梯度思想要求代价函数是可微可导的,若代价函数非凸,就需要迭代步长很小才能实现收敛,计算量大,故收敛速度慢,并且在计算梯度时用瞬时值代替统计平均值,故稳态误差大。
模拟自然界狼群捕猎行为的狼群智能优化算法(Wolf Pack Algorithm,WPA)[4-5],从不同的起点在搜索空间通过狼群中每个个体的适应度值来引导搜索,由于搜索采用的是并行模式,也不需要代价函数的梯度信息,故鲁棒性好,计算量也小,但WPA有时会陷入局部极值。在解决高维非凸性复杂函数的优化问题上WPA表现卓越,将其与BP神经网路算法融合可进行扼流适配变压器的故障诊断;将其与模糊均值聚类算法融合课有效进行图像分割[6-7];将其用于云服务中,能快速准确地从海量云服务中找到既能满足用户需求又具有最优服务质量属性值来进行服务组合[8],但将其用于水声信号的盲均衡研究未见报道。
本文提出了一种改进狼群算法优化的小波常模盲均衡算法(IWPA-WT-CMA),创建了WPA的更新公式,提高了全局寻优能力,用来捕获常模盲均衡算法(WT-CMA)代价函数的最小值,获取最优初始权向量。仿真实验表明,本文算法比CMA以及WT-CMA对水声信道具有更好的均衡性能。
1 小波常模盲均衡算法(WT-CMA)
IWPA-WT-CMA原理框图如图1所示:
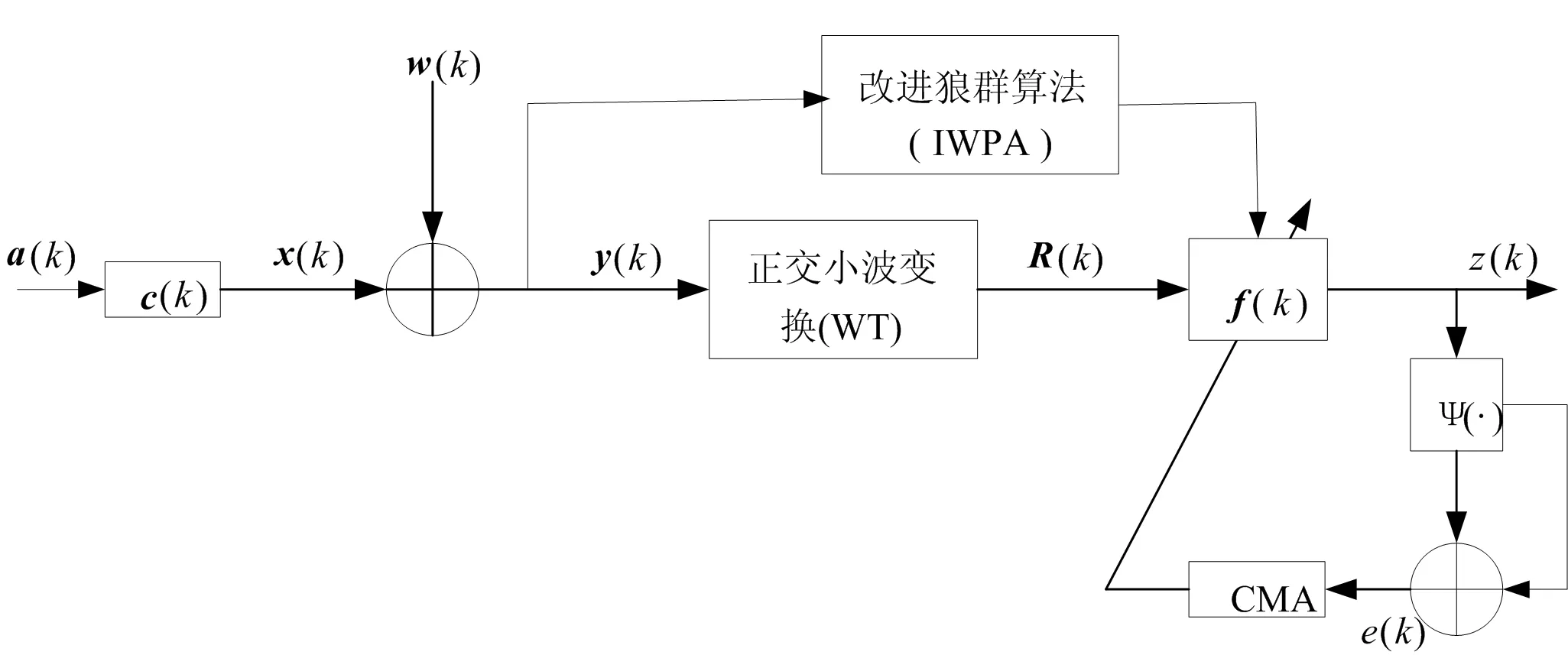
图1 IWPA-WT-CMA原理框图
由图1可知,发射信号a(k)经过脉冲响应向量c(k)(长度为M)的信道,夹杂高斯白噪声w(k),形成y(k),经过小波变换去相关性后成为均衡器的输入信号R(k),f(k)是均衡器权向量系数(长度为2L+1),ψ(·)为无记忆的非线性函数;z(k)是均衡器的输出信号,e(k)为常模误差函数[1]。
设a(k)=[a(k),…,a(k-M+1)]T,y(k)=[y(k+L),…,y(k),…,y(k-L)]T,由图1可得出:
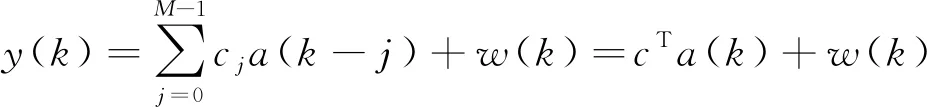
(1)
式(1)中,T表示转置。
R(k)=y(k)Q
(2)
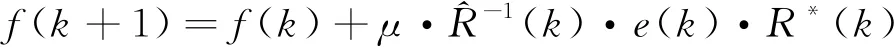
(3)
e(k)=RCM-|z(k)|2
(4)
(5)
z(k)=fT(k)R(k)
(6)
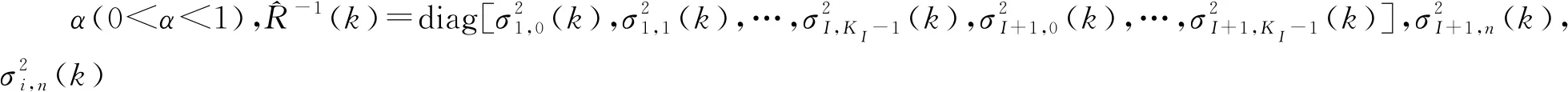
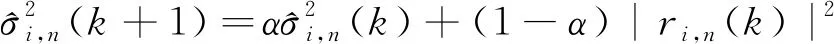
(7)
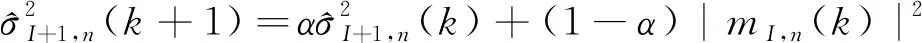
(8)
以上式(1)-(8)构成WT-CMA,其代价函数为:
JWT-CMA=(|z(k)|2-RCM)2
(9)
盲均衡系统理想状态在代价函数取最小值时获得。以上可以看出WT-CMA的代价函数JWT-CMA是非凸性的,但在求取最小值时采用的是随机梯度思想,所以不可避免地存在收敛速度慢,稳态误差大的问题。
2 IWPA-WT-CMA
IWPA-WT-CMA的主要思想是用IWPA最小化WT-CMA的代价函数,利用狼群个体适应度值为指挥棒并行搜索JWT-CMA的最小值。IWPA-WT-CMA流程图如图2所示。
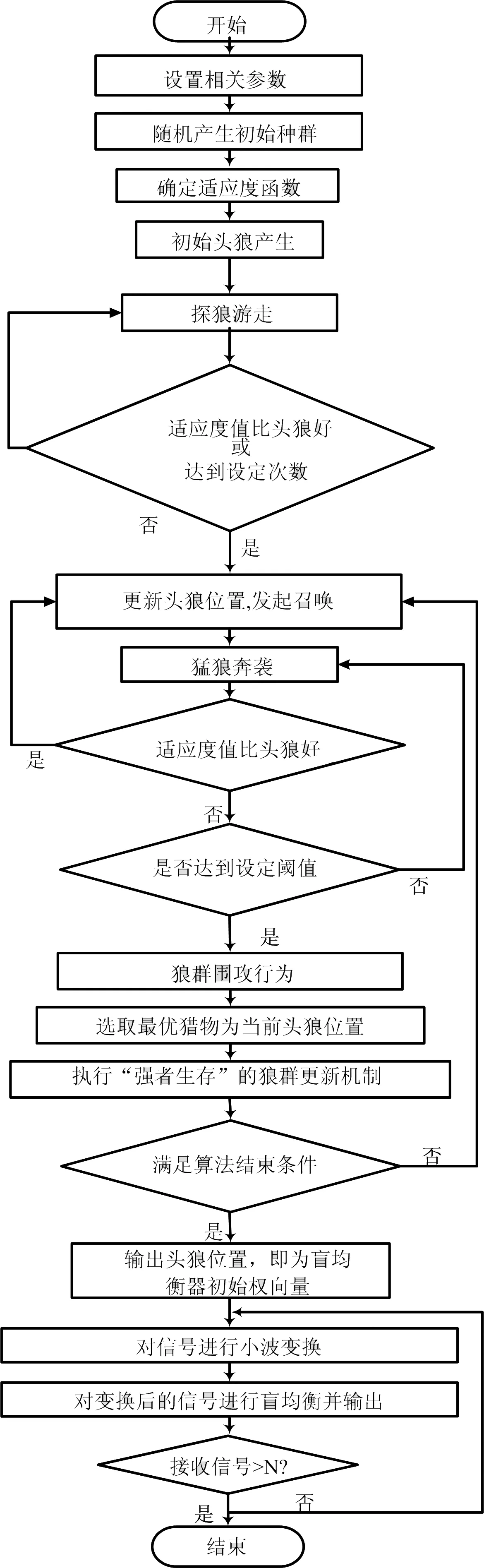
图2 IWPA-WT-CMA流程图
IWPA中狼群通过头狼、探狼、猛狼的分工协作来完成狩猎行为。狼群能识别出猎物的气味浓度,距离猎物越近,人工狼感知到的气味就越强烈,人工狼在算法中对应的适应度函数值就越大。在整个搜寻过程中,谁的适应度值最大,谁就为头狼,负责指挥围剿猎物。在每次攻击之后,淘汰适应度值较差的数匹人工狼,并补充相同数量的新狼,重复探狼游走、猛狼奔袭、共同围剿等一系列活动,直至获取猎物。
根据“强者生存”的思想对每次捕猎完毕的狼群根据适应度值的大小进行更新,是狼群算法的一个特点,一般采用随机的方式生成补充的新狼,这样新狼有可能比淘汰的人工狼适应度值更差,不利于快速全局寻优,因此本文对这一点进行了改进。IWPA具体步骤如下:
2.1 初始化阶段
在D维搜索空间按公式(10)随机分配N匹狼位置,第n匹狼的位置可以用一个D维的向量表示:
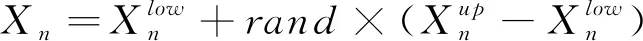
(10)
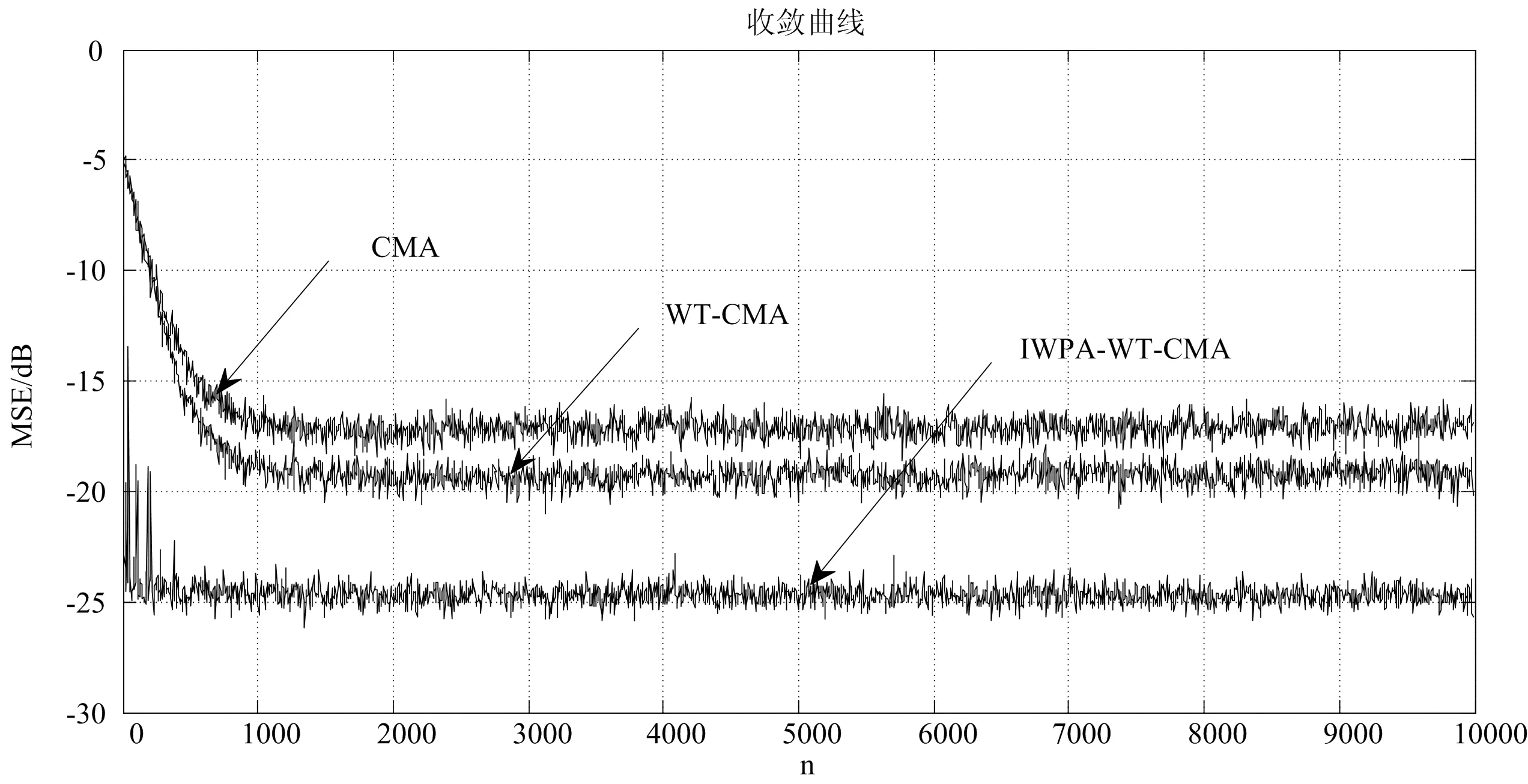
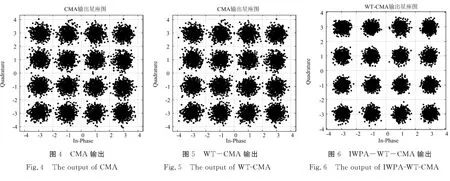
式(10)中,n=1,2,…,N,Xlow和Xup分别为位置向量X的下界和上界,即Xlow 适应度函数值是IWPA寻优的指挥棒,狼群的移动一直向着适应度函数P(X)最大的方向逐步推进,最终得到全局最大值,而盲均衡算法中是要获取代价函数J(X)的最小值,两者关系可如式(11)所示: (11) 计算初始狼群中所有人工狼对应的适应度值并进行排序,具有最大适应度值的为初始头狼。 (12) 式(12)中,h=1,2,…,H,s=1,2,…,S,d=1,2,…,D。 在游走搜寻过程中,如果探狼比头狼的适应度值大,则其成为新的头狼,结束游走行为;否则重复游走,直至出现新的头狼,或者达到游走次数设定值结束。 狼群在适应度值的更新指引下,结束游走探寻,距离猎物最近的头狼召唤猛狼向猎物方向靠近。k+1次迭代时,猛狼的位置为: xnd(k+1)=xnd(k)+stepb×(gd(k)-xnd(k))/|gd(k)-xnd(k)| (13) 式(13)中,n=1,2,…,N-S-1,stepb为猛狼的移动步长,gd(k)为k代头狼的位置。移动过程中,若猛狼的适应度函数值大于头狼的适应度值,则成为新的头狼,重新发起召唤行为;否则,猛狼按式(13)移动到预设范围(一般要求猛狼与头狼之间的距离dis小于判定距离dnear时停止): (14) 头狼最接近猎物,在围攻行为中将头狼的位置gd(k)视为猎物的位置Gd(k)。 xnd=xnd(k)+λ×stepc×|Gd(k)-xnd(k)| (15) 除头狼外的其他N-1匹狼按式(15)以stepc接近猎物并伺机围攻,λ为均匀分布在[-1,1]的随机数。围攻过程中,根据适应度函数值的变化判断进攻是否有利,是否需要更新自己的位置,若适应度值变大,视为有效进攻,则更新位置,若适应度值变小则退回原位。 stepa=stepb/2=2×stepc=|XU-XL|/φ (16) 式(16)中,φ为步长因子,用来控制搜寻的精细程度。 WPA的每一次围攻行为结束后,都会将群体中适应度值较低的O匹狼淘汰,并按公式(10)生成O匹新狼。新狼是随机产生的,可能还不如淘汰的人工狼优良,无法体现“强者生存”思想。本文改进了这种淘汰更新机制。设在算法第t代中,消失的第i匹狼按公式(17)重生: (17) 式(17)中,i=1,2,…,O,t=1,2,…,Tmax,Tmax为最大迭代次数,X*为头狼位置,randn为均值为0方差为1的正态分布,θ作为调节因子控制新狼群的质量。 头狼一直是适应度值最大的。若满足算法结束条件,此时头狼对应的适应度函数值即为全局最大值,输出最大值,IWPA算法结束,若将WT-CMA代价函数的倒数作为IWPA的适应度函数,则此时X*即为所求的盲均衡器最优初始权向量;否则转入探狼游走,继续进行迭代。 为了验证该算法的有效性,以CMA、WT-CMA为比较对象,进行仿真实验。信道h=[0.965 6,-0.090 6,0.057 8,0.236 8],发射信号的采样点均为10 000点的16QAM信号,CMA中的步长μCMA=0.000 007,WT-CMA中的步长μWT-CMA=0.000 04,IWPA-WT-CMA中的步长为μIWPA-WT-CMA=0.000 021,信噪比为20 dB,400次蒙特卡诺仿真结果如图3~6所示。 图3 均方误差 由图4~6中可以看出:在稳态均方误差方面,IWPA-WT-CMA比WT-CMA、均方误差都小,收敛速度也明显加快;3种算法中IWPA-WT-CMA的输出星座图较CMA-WT-CMA更为清晰、紧凑,恢复出的传输信号更为准确。 本文提出了改进狼群算法优化的小波常模盲均衡算法(IWPA-WT-CMA),以解决常模盲均衡算法中因代价函数优化问题带来的收敛速度慢、稳态误差大等问题。本文算法创建了模拟自然界狼群捕猎行为的狼群智能优化算法中"强者生存"(WPA)的更新公式,通过初始化阶段、初始头狼生成、探狼游走、召唤奔袭、围攻行为、狼群更新六个步骤,提高了算法的全局寻优能力,将改进后的狼群算法用于获取WT-CMA代价函数最小时对应的均衡器初始权向量,可有效提升盲均衡器的性能。通过仿真实验可验证,与常模盲均衡算法(CMA)和小波常模盲均衡算法(WT-CMA)对比,本文算法最为有效,星座图更为清晰、紧凑,不仅收敛速度快,而且稳态误差小,更利于水声信号的实时恢复。2.2 确定适应度函数
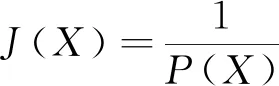
2.3 初始头狼生成
2.4 探狼游走
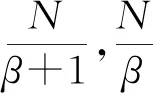
2.5 召唤奔袭
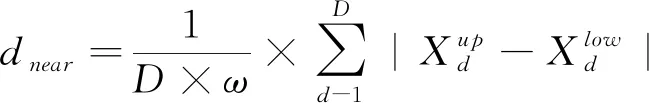
2.6 围攻行为
2.7 狼群更新
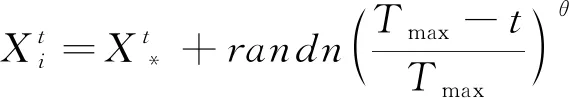
3 仿真实验
4 结语

