基于中心逼近式的GM(1,1)模型在变形预测中的应用

江春建

（河北建设勘察研究院有限公司，石家庄050000）

1 引言

由于影响变形体变形的因素复杂多变，随着时间的推移，观测数据中将不可避免地存在着一些随机扰动误差，使变形体变形曲线发生异常波动，在进行长期预测时，预测值往往偏高或偏低，因而对随机波动性较大的数据列拟合较差，预测精度低[1，2]。灰色预测模型是基于最小二乘法的指数拟合曲线中但当用纯指数序列进行拟合时，却又不能完全取得满意的拟合效果，往往产生偏差。中心逼近式GM（1，1）模型可以弱化序列变化的幅度，减小数据波动,弱化随机性。经数据模拟和比较发现，中心逼近式GM（1，1）模型比传统的GM（1，1）模型有较高的模拟精度和预测精度。

本文根据某一高层建筑物的沉降观测资料，通过使用中心逼近式GM（1，1）模型进行预测，证明了该模型在建筑物变形预测中具有明显的优越性。

2 中心逼近式GM(1,1)模型的建立

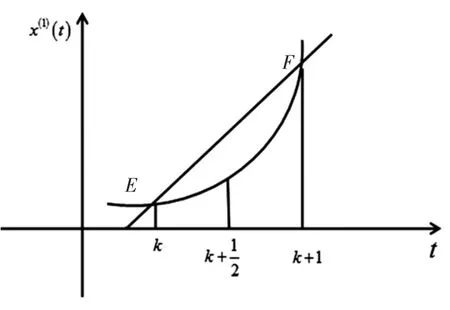
图1 背景值取值示意图

中心逼近式方法的核心思想是[3]：先对一次累加序列开m次方，记为并且记：

利用最小二乘原理求出参数a和b，解式（3）微分方程可得：

则微分方程的时间响应函数：

3 算例分析

本文以某市一高层建筑物的沉降数据为算例，选取该建筑物连续观测30 期的时序数据作为研究对象。利用前20 期的观测值建立预测模型，用后10 期数据对模型进行检验预测，然后与已有的观测值进行比较，以此来检验中心逼近式灰色模型的预测精度。原始观测数据如表1 所示。

表1 原始观测数据

3.1 传统灰色模型的建立

通过matlab 软件运行程序可以得出模型的参数值，模型的参数a和b分别为-0.0409、8.8920。所得的离散时间响应函数为：

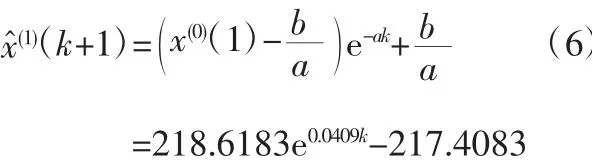
根据建立的GM（1，1）模型对建筑物的第21～30 期变形数据进行预测，其预测结果如表2 所示。

表2 传统灰色模型预测结果

3.2 用中心逼近式GM(1，1)建立模型

通过实验分析选取m=2 时模型的拟合效果较好，且原始数据序列呈指数规律[5]，运行matlab 程序可得出预测结果，其预测结果如表3 所示。

表3 改进的灰色模型预测值

3.3 模型的精度检验

对传统模型与本文采用模型的预测值和原始观测值作图进行比较，由图2 可知，用中心逼近式灰色模型与观测值拟合较好，预测值更加接近于实测值，预测精度较高，从整体上反映了本文采用模型的预测效果明显优于传统模型。

由表4 中各个误差指标的对比可知，本文采用模型的每项精度指标都比传统模型小，预测精度较高。如中心逼近式GM（1，1）模型的平均相对误差为3.105%，而传统模型的平均相对误差为6.0148%。这表明本文所采用的中心逼近式GM（1，1）模型对建筑物预测能够得到较好的预测精度。

图22 种模型预测值与观测值比较

表4 误差指标对比

4 结语

本文采用中心逼近式GM（1，1）模型对某一高层建筑物进行沉降分析与预测，从实例对比分析可以看出，相比于传统模型，该模型具有较好的预测精度和稳定性[6]，其预测效果优于传统的灰色模型。在建筑物的沉降变形预测中，单一模型还存在着不足和缺点，而把单个模型进行组合，构建组合预测模型是目前发展的趋势，需要做进一步的探讨。