附合导线角度闭合差计算的多边形辅助线法
李啸天,覃超,王旭华
(大连大学 建筑工程学院,辽宁 大连 116622)
1 引 言

一些学者[3~5]通过几何推导的方法,经过各导线点做南北方向辅助线来简化计算过程,但计算效率仍然较低。本文通过对附合导线作辅助线将其转化为闭合多边形,则附合导线角度闭合差的计算即为多边形内角和与其理论值之差。本文提出的附合导线角度闭合差计算的多边形辅助线法避免了传统方法在推算坐标方位角时要逐点区分各角为左角还是右角、逐边分析是否加减180°的判断过程,减少了计算量,提高了计算效率。实际授课表明,附合导线角度闭合差计算的多边形辅助线法比传统方法更容易被学生接受,教学效果良好。
2 附合导线转化为闭合多边形及其角度闭合差计算
2.1 附合导线转化为闭合多边形方法
根据不同的附合导线布设形式,在其两已知端点A、D分别作竖直或水平方向的辅助线,再依次连接各边构成闭合多边形,使所有观测角均为多边形的内角。需要注意的是,在此过程当中不必区分各导线点的观测角是左角还是右角,新构成的闭合多边形除了已有的各观测角外,还新增加了几个不含“误差”的内角。
2.2 转化后的角度闭合差计算
图1~图8列出了各种形式的附合导线,现以图1为例说明附合导线角度闭合差计算的辅助线法的应用过程,并与现有测量学教材上附合导线角度闭合差的计算方法及结果加以比较。
(1)测量学教材中附合导线角度闭合差的计算

这里按推算方向各观测角应为左角,则各边坐标方位角推算如下:
αB1=αAB+βB-180°
α12=αB1+β1-180°
α2C=α12+β2-180°
这里,各边的坐标方位角的计算公式均取“-180°”,是因为其前两项之和均大于180°。
将以上各式相加,得:
则角度闭合差:
fβ=αAB-αCD+∑β-4×180°
(1)

图1 附合导线类型一
(2)附合导线角度闭合差计算的多边形辅助线法
附合导线类型一的特点:自A、D两个已知端点向上做X轴平行辅助线AF、DE不与其他导线边相交。如图1所示,使所有观测角为内角,连接E、F两点,得闭合多边形AB12CDEFA。其中:需要观测的角度个数n=4,新增角度4个,设闭合多边形边数为N,则N=n+4=8。
在多边形中:∠E+∠F=180°,∠A=αAB,∠D=180°-αCD
显而易见,附合导线角度闭合差即为该多边形内角闭合差,该多边形角度闭合差为:
fβ=∠A+∠D+∠E+∠F+∑β-(N-2)×180°
=αAB-αCD+∑β-4×180°
此结果与式(1)的附合导线角度闭合差fβ的推算公式完全相同。
2.3 对比分析
对比两种方法的过程和结果可知,二者均能准确地求出附合导线的角度闭合差,但是教材上所提供的方法需要依次推算各导线边的坐标方位角,且需逐边判断αi+βi与180°的大小关系,边数越多,计算量越大,容易造成计算错误。而通过做辅助线,将附合导线角度闭合差转为多边形内角闭合差计算的方法则相对简便,内业计算较小,提高了工作效率。
2.4 其他类型的附合导线及其多边形辅助线法
按照图1类似的方法与过程,可做出其他不同类型的附合导线(图2~图8)的多边形辅助线,并推算出相应的角度闭合差。具体过程不一一详述。
(1)附合导线类型二。该类导线特点是:自A点向上做X轴平行线不与其他导线边相交,自D点向上做X轴平行线会与其他导线边相交,需向右做水平线,构成闭合多边形AB12CDEFGA。
其中:n=4,N=n+5
∠G+∠F=180°,∠E=90°
∠A=αAB,∠D=270°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∑β-(N-2)×180°
=αAB-αCD+∑β-n×180°
(2)

图2 附合导线类型二
(2)附合导线类型三。该类导线特点是:自A点向上做X轴平行线不与其他导线边相交,自D点向上做X轴平行线或向右做水平线都会与其他导线边相交,需向下做X轴平行线,构成闭合多边形AB12CDEFGHA。

图3 附合导线类型三
其中:n=4,N=n+6
∠E+∠F=180°,∠G+∠H=180°
∠A=αAB,∠D=360°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∠H+∑β-(N-2)×180°
=αAB-αCD+∑β-n×180°
(3)
(3)附合导线类型四。该类导线特点是:自A点向上做X轴平行线会与其他导线边相交,需向左做水平线,自D点向上做X轴平行线不与其他导线边相交,构成闭合多边形AB12CDEFGA。

图4 附合导线类型四
其中:n=4,N=n+5
∠E+∠F=180°,∠G=90°,
∠A=αAB-270°,∠D=180°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∑β-(N-2)×180°
=αAB-αCD+∑β-(n+2)×180°
(4)
(4)附合导线类型五。该类导线特点是:自A点向上做X轴平行线或向左做水平线都会与其他导线边相交,需向下做X轴平行线,自D点向上做X轴平行线不与其他导线边相交,构成闭合多边形AB12CDEFGHA。

图5 附合导线类型五
其中:n=4,N=n+6
∠E+∠F=180°,∠G+∠H=180°
∠A=αAB-180°,∠D=180°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∠H+∑β-(N-2)×180°
=αAB-αCD+∑β-(n+2)×180°
(5)
(5)附合导线类型六。该类导线特点是:自A点向上做X轴平行线会与其他导线边相交,需向左做水平线,自D点向上做X轴平行线会与其他导线边相交,需向右做水平线,构成闭合多边形AB12CDEFGHA。

图6 附合导线类型六
其中:n=4,N=n+6
∠E=∠H=90°,∠F+∠G=180°
∠A=αAB-270°,∠D=270°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∠H+∑β-(N-2)×180°
=αAB-αCD+∑β-(n+2)×180°
(6)
(6)附合导线类型七。该类导线特点是:自A点向上做X轴平行线或向左做水平线都会与其他导线边相交,需向下做X轴平行线,自D点向上做X轴平行线会与其他导线边相交,需向右做水平线,构成闭合多边形AB12CDEFGHIA。
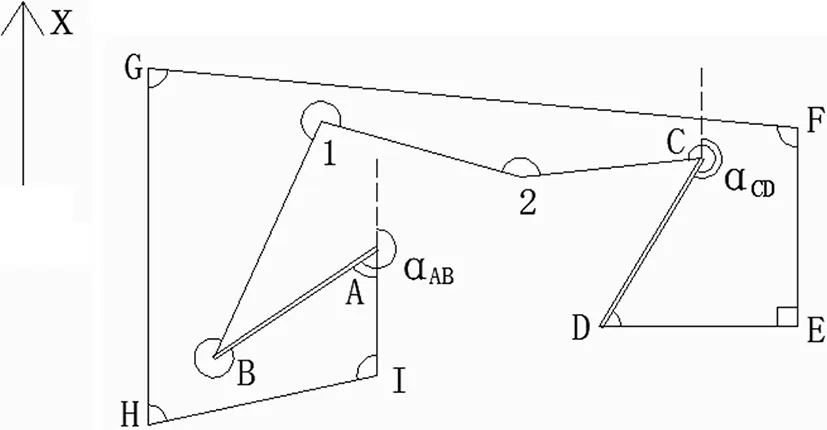
图7 附合导线类型七
其中:n=4,N=n+7
∠E=90°,∠F+∠G=180°,∠H+∠I=180°
∠A=αAB-180°,∠D=270°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∠H+∠I+∑β-(N-2)×180°=αAB-αCD+∑β-(n+2)×180°
(7)
(7)附合导线类型八。该类导线特点是:自A点向上做X轴平行线或向左做水平线都会与其他导线边相交,需向下做X轴平行线,自D点向上做X轴平行线或向右做水平线都会与其他导线边相交,需向下做X轴平行线,构成闭合多边形AB12CDEFGHIJA。

图8 附合导线类型八
其中:n=4,N=n+8
∠E+∠F=∠G+∠H=∠I+∠J=180°
∠A=αAB-180°,∠D=360°-αCD
fβ=∠A+∠D+∠E+∠F+∠G+∠H+∠I+∠J+∑β-(N-2)×180°=αAB-αCD+∑β-(n+2)×180°
(8)
2.5 计算示例
附合导线的坐标方位角及各导线观测角如图8所示,前进方向A→D,现使用上述多边形辅助线法计算该附合导线角度闭合差。该例取自文献[1]。

图9 计算示例
过程如下,自A、D两个已知端点向上做竖直辅助线AF、DE,如图9所示,使所有观测角为内角,连接E、F两点,得闭合多边形AB1234CDEFA。其中:需要观测的角度个数n=6,新增角度4个,设闭合多边形边数为N,则N=n+4=10。
在多边形中:∠E+∠F=180°,∠A=αAB,∠D=180°-αCD
显而易见,附合导线角度闭合差即为该多边形内角闭合差,该多边形角度闭合差为:
fβ=∠A+∠D+∠E+∠F+∑β-(N-2)×180°=αAB-αCD+∑β-n×180°
=237°59′30″-46°45′24″+99°01′00″+167°45′36″+123°11′24″+189°20′36″+179°59′18″+129°27′24″-6×180°
=-36″
3 结 论
(1)辅助线法将附合导线角度闭合差计算转化为多边形内角和闭合差的计算,不用逐边分析是否需要加减180°简化了推算过程,提高了工作效率。
(2)通过对8种类型的附合导线角度闭合差的计算可知,其结果只有两种形式:αAB-αCD+∑β-n×180°或αAB-αCD+∑β-(n+2)×180°,区别仅仅在于180°前的系数是“n”或者“(n+2)”,且该结果只与已知边AB的方位有关,若过A点向上做X轴平行线不与其他导线边相交(如图1、图4、图5所示),则“n”;否则(如图2、图3、图6、图7、图8所示),该系数为“(n+2)”。

