拖体粘性类水动力系数计算方法研究
陈小星 赵林建
(第七一五研究所,杭州,310023)
随着主动拖曳声呐的广泛使用,对拖体的水动力数值模拟方法研究也逐渐在设计中广泛采用,相对以往的工程近似估算,该方法精度有明显提高。同时与水池试验相比,具有成本低、周期短等优点。文献[1,2]对粘性水动力系数进行了数值计算方法研究,采取Fluent软件进行计算,通过二次编程增加动量源项,将旋臂试验转换为定常计算研究。本文以Star-CCM+为计算软件,采用场函数直接添加动量源项,避免了复杂的编程。通过数值计算仿真并与实测数据进行了比对,表明该方法可以用于方案设计阶段,计算结果可以达到工程使用要求。
1 数值模型
1.1 源项计算
在惯性坐标系下,流体的连续性方程为
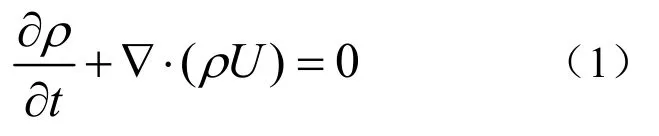
动量RANS(Reynolds-Averaged Navier-Stokes)方程为
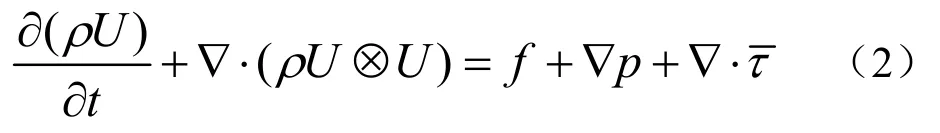
式中,ρ表示流场密度,U为流场速度,f为体积力,为流体应力张量,在角速度为常数Ω的旋转参考系下,连续性方程没有速度的导数项,保持不变,RANS方程变为

式中,Ur为相对速度,r为旋转半径。相对惯性坐标系下的增加项MS为
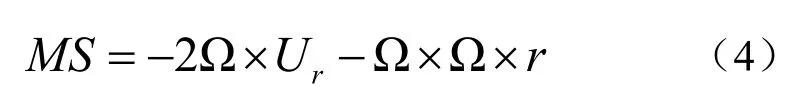
额外增加的体积力MS,可以作为动量源项添加进流场中,从而实现稳态计算,避免了Star-CCM+中采用旋转参考系的复杂做法。
1.2 k-e湍流模型
湍动能k、湍流耗散率ε的传输方程为
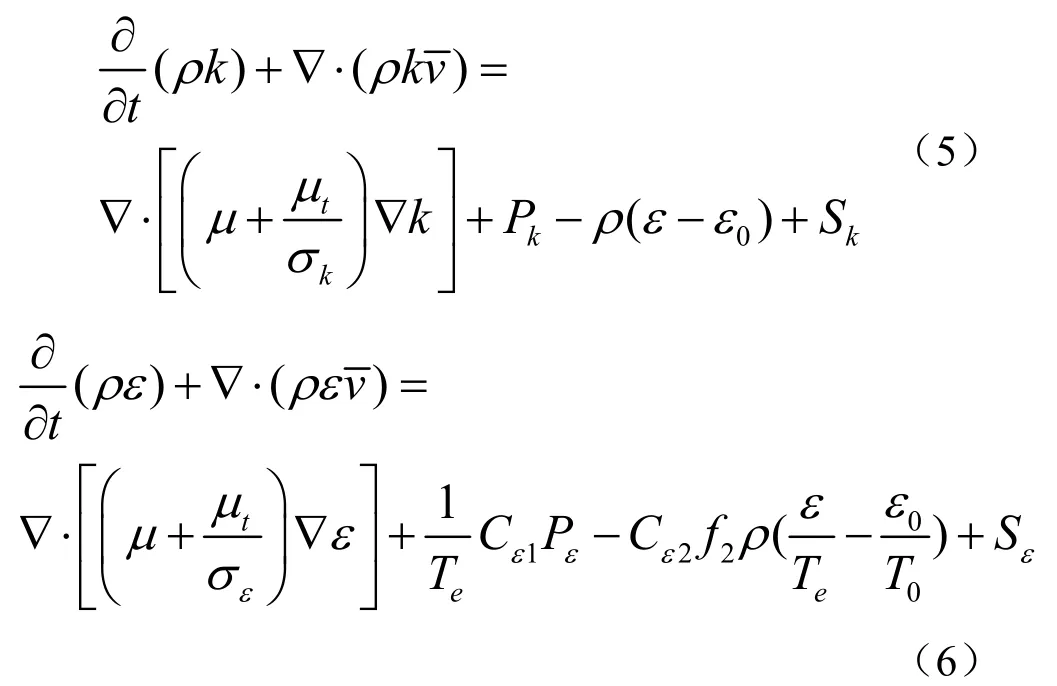
式中,为平均速度,μ为动力粘度,ρ为流体密度,μt为湍流涡粘度,σk、σε、Cε1、Cε2为模型系数,Sk、Sε为用户指定的源项。
1.3 k-ω湍流模型
k-ω湍流模型是双方程模型,它可对湍动能k和单位耗散率ω的传输方程进行求解,以确定湍流涡粘度。一般适用于强旋湍流,本文中悬臂计算采用k-ω湍流模型。其传输方程为
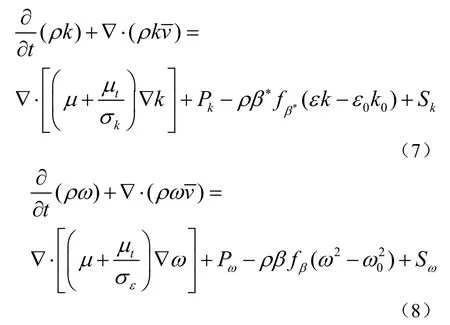
式中,β*、β为模型系数,Pk、Pω为结果项。
2 直航试验
2.1 流体域及网格划分
为消除计算域壁面对流动的影响,流域范围应越大越好,但这必然会导致网格数量过大影响计算效率。本文选择矩形计算流域,为保证模型周围流场得到充分发展,长宽高为13 m×6 m×6 m,采用六面体网格。
采用k-e湍流模型进行仿真计算,确保Wall Y+都在30~300之间。首层边界层厚度公式如下[3]:
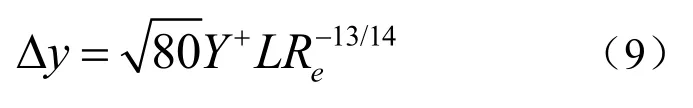
式中,Y+为期望的取值,这里取100,L为拖体特征长度,Re为雷诺数。边界层数量为6层,边界层总厚度为0.02 m。计算收敛后,查看计算的Y+分布如图1所示,大部分拖体表面的Y+值都在30~300之间。
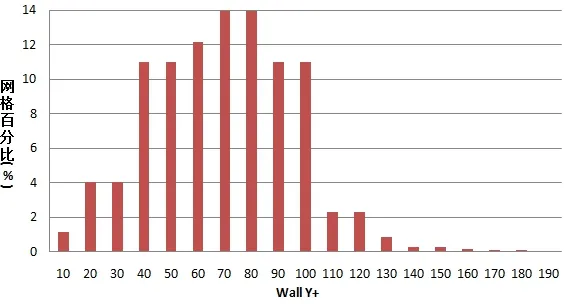
图1 拖体表面Wall Y+分布图
对模型进行了网格无关性验证,建立了四套网格分别进行计算,按照ITTC(International Towing Tank Conference)推荐设定,BaseSize按2比率缩小,计算结果见表1。选择网格4的大小,模型的阻力变化不大,本文计算选择BaseSize为0.025 m。
航标是引导船舶安全航行的重要设施,是我国海事安全保障体系的重要组成部分,航标可靠的导助航效能是船舶安全通航的保障。伴随着科学技术的发展,航标科技的发展也越来越快,我们有理由相信,未来航标维护管理工作肯定会比现在更加的科学、安全和可靠。

表1 网格数量与阻力关系表
2.2 边界条件和求解器设置
本文一共使用了4种边界条件:(1)上游壁面为速度入口,给定来流方向及大小;(2)四周壁面为滑移壁面;(3)下游壁面为压力出口;(4)拖体表面为无滑移壁面。使用分离求解器,离散方式采用二阶迎风格式,收敛标准选取为10-5,迭代步数为1 000步。
2.3 试验结果
直航试验主要计算各个拖曳速度下的纵向阻力,用来确定纵向阻力系数速度下的中纵剖面的速度分布及压力分布见图2、图3。计算阻力和实验阻力拟合曲线见图4。
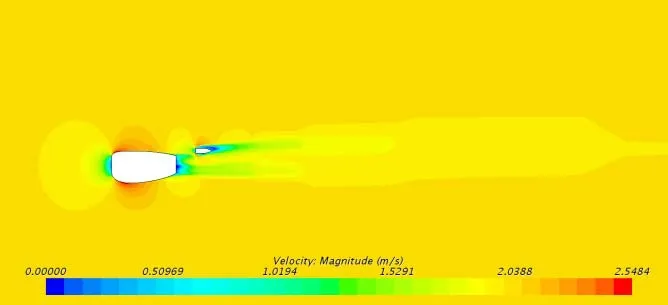
图2 中纵剖面速度分布图
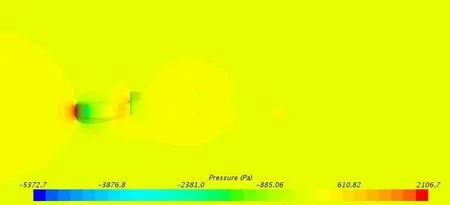
图3 中纵剖面压力分布图
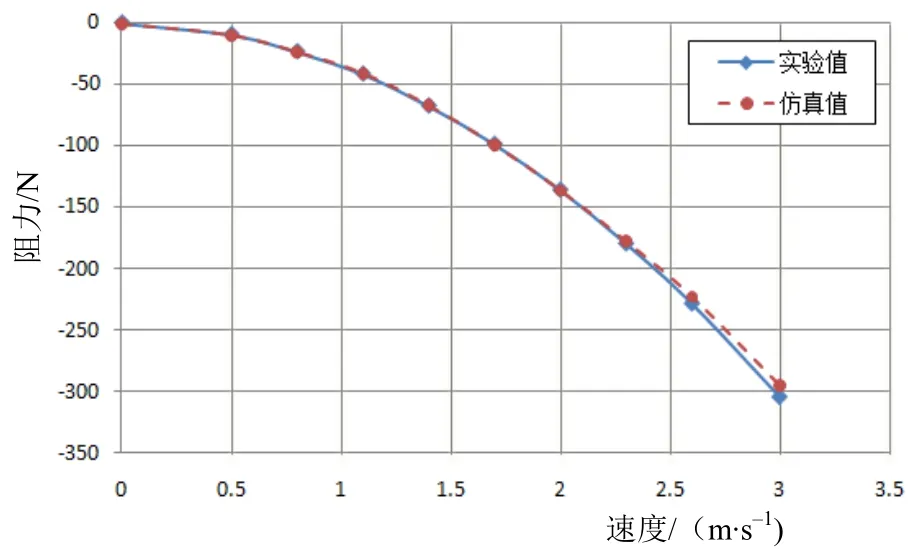
图4 各拖曳速度下的阻力
对计算获得的数据进行整体线性回归分析,取得拖体的纵向阻力系数,无因次化后结果为与水池试验的无因次结果进行比较,误差为6.7%。
3 斜航试验
斜航试验用来确定由速度引起的水动力系数,主要为位置导数 (水平面及垂直面位置导数通过拟合Y-v、N-v、Z-w、M-w曲线获得。斜航试验的计算工况见表2,通过调整拖体的偏转角度计算各个流体力及流体力矩。所有工况的来流速度为2m/s。

表2 斜航试验数值模拟计算工况
斜航试验采用与阻力试验相同的网格尺寸、边界条件和求解器设置,只是模型进行偏转。其Y-v、N-v、Z-w、M-w曲线的对比如图5~8所示。
对仿真结果采用整体回归分析方法,得到水平面和垂直面的位置导数,进行无因次化后的结果见表3。除了结果偏差略大,其余的水动力系数误差均在10%以内。
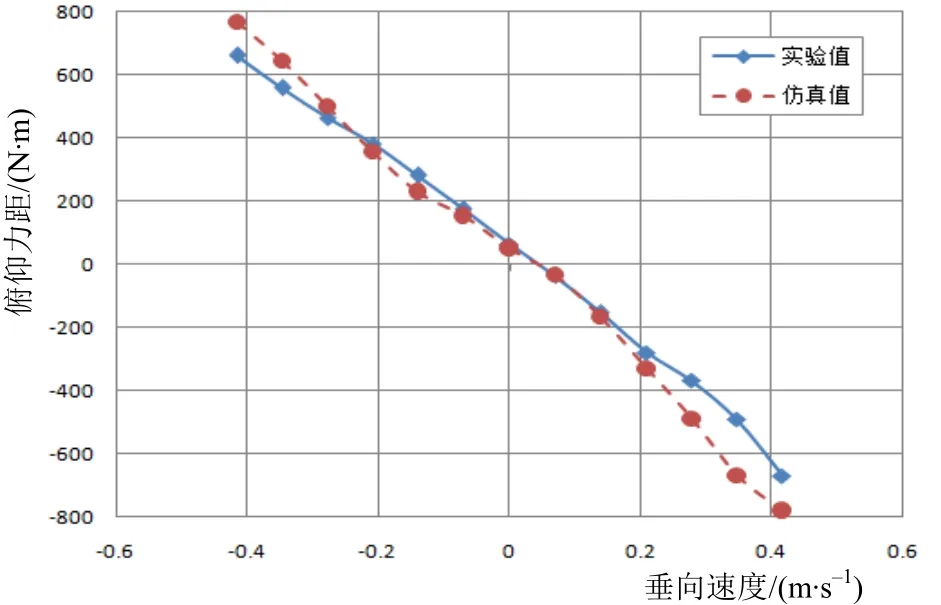
图5 俯仰力矩M-垂向速度w曲线
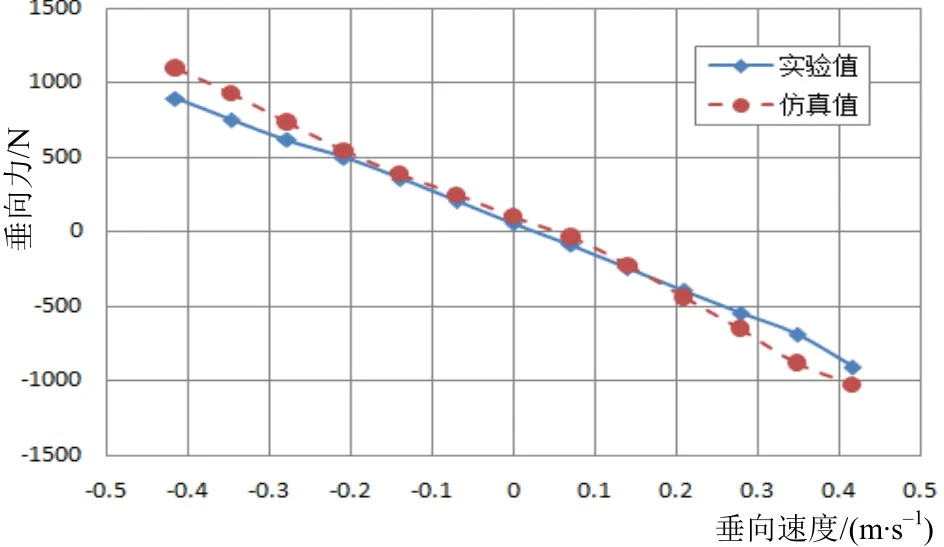
图6 垂向力Z-垂向速度w曲线
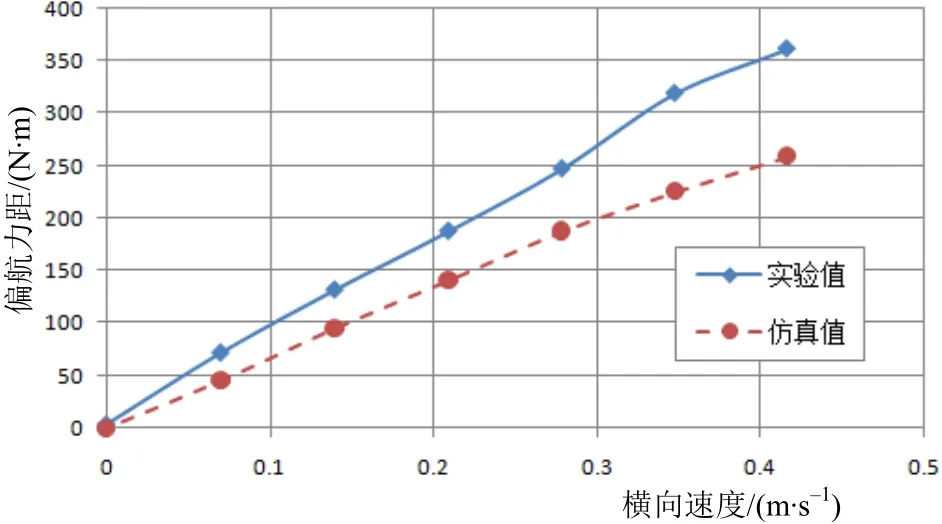
图7 偏航力矩N-横向速度v曲线
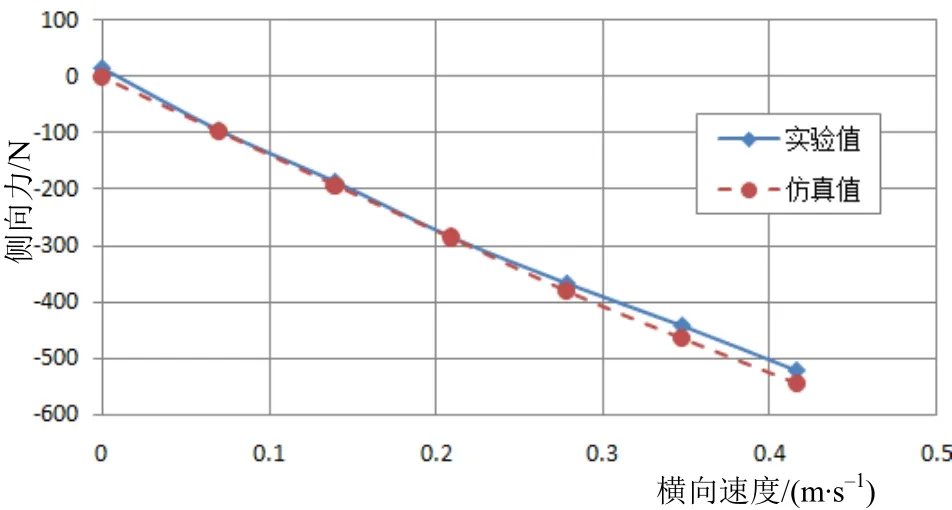
图8 侧向力Y-横向速度v曲线
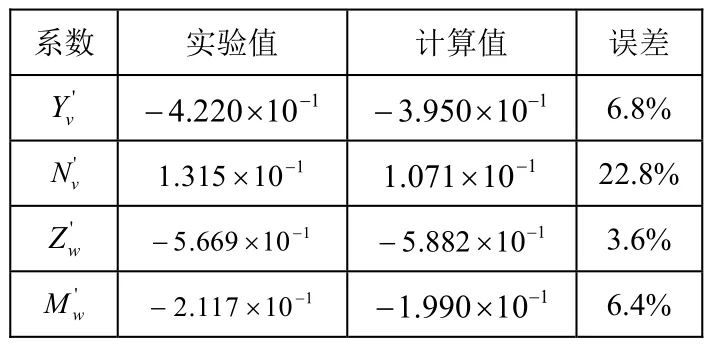
表3 斜航试验数值模拟计算结果
4 旋臂试验
旋臂试验主要用来确定由角速度引起的水动力系数,主要是旋转导数 (水平面以及垂直面旋转导数通过拟合Y-r、N-r、Z-q、M-q曲线获得。旋臂试验的计算工况见表4。通过调整拖体的回转半径计算各个流体力及流体力矩。所有工况的来流速度为2m/s。

表4 旋臂试验数值模拟计算工况
旋臂试验采用回转体流域,边界条件和求解器设置与斜航试验相同,为了提高收敛效率,采用多面体网格k-ω湍流模型进行仿真计算。
对增加的源项MS,在求解区域中按式(4)增加了动量源项场函数。同时入口速度指定为Ω×r场函数。
边界层厚度确定按照式(9)进行计算,取Y+=4,边界层数量20层,边界层总厚度为0.03 m。计算收敛后,Y+分布见图9,图中大部分拖体表面的Y+值都在5以下,其Y-r、N-r、Z-q、M-q计算曲线见图10~11,其回转半径R=30 m下的速度分布见图12。
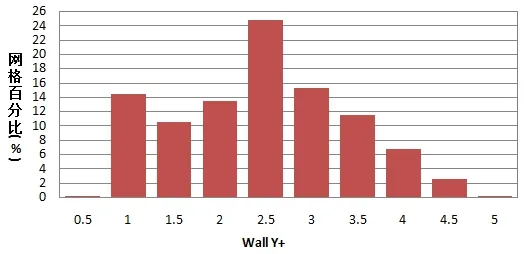
图9 拖体表面Wall Y+分布图
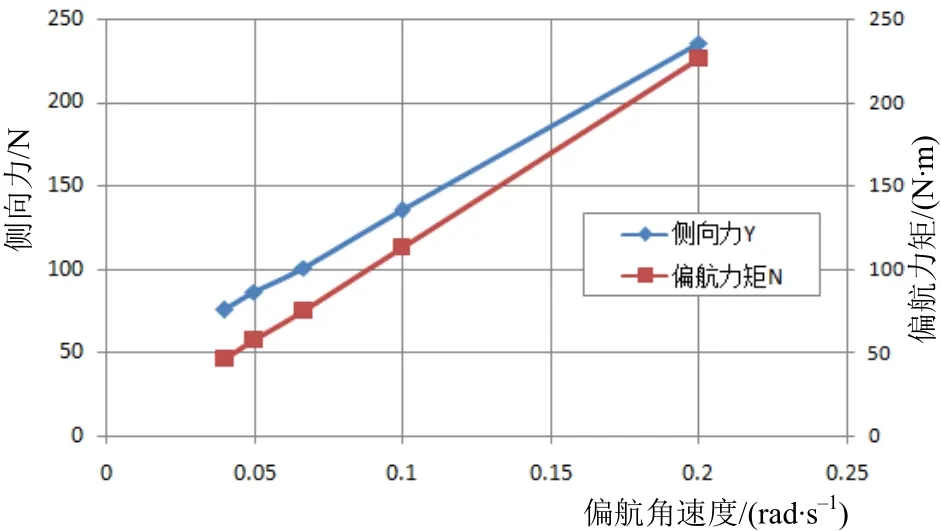
图10 侧向力Y、偏航力矩N-偏航角速度r曲线
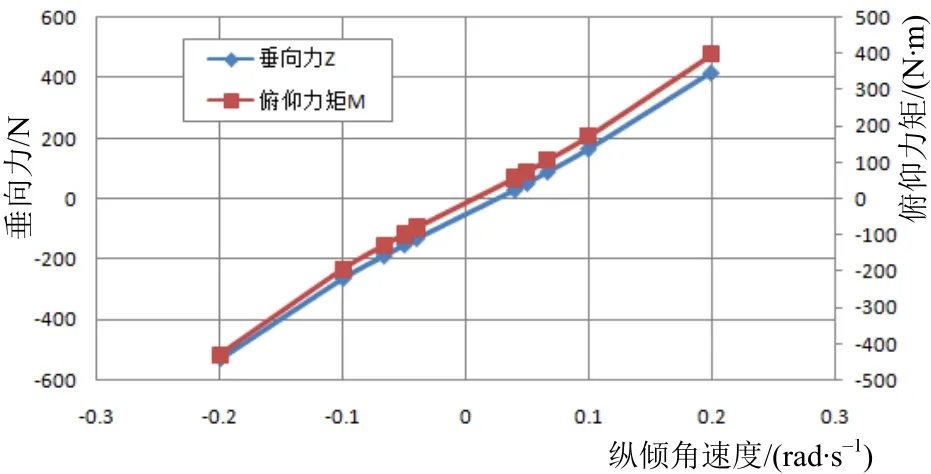
图11 垂向力Z、俯仰力矩N-纵倾角速度q曲线
图12 2m/s速度、R=30 m时回转速度分布图
对仿真结果采用整体回归分析方法,得到水平面和垂直面的旋转导数,进行无因次化后的结果见表5。从表中数据可知,误差都在20%以内。
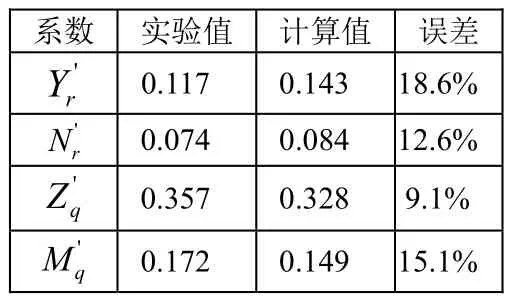
表5 旋臂试验数值模拟计算结果
5 结论
本文通过仿照拖体的运动形式,采用两种湍流模型,对拖体水动力系数进行了数值模拟计算,通过使用附加动量源项方法,将瞬态计算转换为稳态计算,大大缩短了计算时间。同时将计算结果与试验数据进行了比对,验证了该方法的可行性,计算结果可以满足工程使用精度要求。本文的研究可以应用于拖体方案设计阶段的稳定性和操纵性预报,从而缩短开发周期,降低开发成本,对拖体的水动力系数计算有一定的参考价值。

