平直条带流致振动特性实验及其数值模拟研究

（上海交通大学 核科学与工程学院，上海200240）

当压水堆核电厂正常运行时，由燃料组件核裂变反应释放的热量经由流过的冷却剂带走.然而，高流速的冷却剂会使燃料组件产生振动，即流致振动.流致振动会导致格架条带与燃料棒包壳之间发生磨损，当磨损超过一定限值后，燃料棒包壳结构将被破坏，从而影响核电厂运行的安全性.根据国际原子能机构（IAEA）压水堆堆内运行经验报告[1]，流致振动是导致燃料棒破损的主要原因.流致振动主要有3种机理：湍流随机激励、旋涡脱落激励和流弹失稳.其中，在横向来流的情况下，由旋涡脱落激励引起的涡激振动是反应堆格架条带的主要振动机理.

许多学者针对反应堆燃料组件的流致振动特性开展了相关的实验及数值研究.张晓玲等[2]采用实验的方法研究燃料组件的振动特性及流致振动响应，获得各稳态工况的流致振动响应规律.Liu等[3]对燃料组件中燃料棒的流致振动特性进行了数值模拟，发现燃料棒的振动频率集中在其固有频率附近.卢川等[4]采用大涡模拟方法对燃料组件格架外条带区域的流场和压力场进行瞬态计算，发现格架在不同区域具有不同的压力波动特性.然而，目前对格架条带本身的振动特性及其流致振动机理研究得较少.对于涡激振动，研究主要集中于圆柱和方柱的绕流.Williamson 等[5]、Khalak 等[6]和 Govardhan等[7]对圆柱涡激振动进行了系统的研究，全面地阐述了阻尼和质量比等参数对振动幅值、尾涡形态的影响.Sumer等[8]的研究表明，随着折减速度的增大，当折减速度达到一定值时，柱体的振动频率、旋涡脱落频率与固有频率接近或者相等时，会发生“锁定”和共振现象.胡德江[9]对方柱的流致振动进行了风洞实验研究，获得了旋涡脱落频率与方柱振动频率随着流速变化的曲线.徐枫等[10]对方柱的涡激振动进行计算流体力学（CFD）模拟，同样观察到在旋涡脱落频率接近固有频率时，将会产生明显的“锁定”现象.

为了探索燃料组件格架条带流致振动的研究方法及其物理机理，设计并进行了透明矩形流道内不带结构的平直条带流致振动实验，采用激光多普勒测振仪（LDV）获得了平直条带流致振动响应.同时结合湿模态模拟，获得了平直条带的流致振动特性.

1 实验研究

1.1 实验装置

平直条带流致振动实验的回路结构如图1所示.水箱中的去离子水由变频离心泵驱动，经过实验段后回流到储水罐.实验回路中，采用涡轮流量计测量流过实验段的流量.为了减少回路中的压力脉动，在实验段进口设置稳压器；为了研究燃料组件格架条带的流致振动物理机理，且研发其相应的理论模型，采用平直条带作为实验对象，窄矩形通道作为流道.实验段及不锈钢条带格架的位置如图2所示.流道采用透明亚克力材质；矩形流通道的尺寸为66 mm×12mm×2 040mm，两端由法兰连接并刚性固定于实验台架上；不锈钢条带的厚度取格架条带的厚度，即h＝0.46mm；流向长度为中间格架条带的长度，即Z＝10.6mm，展向长度X＝66mm；不锈钢条带置于流道的中间位置，条带展向的两端采用矩形块压紧固定，并用螺丝钉将其固定于流道侧壁.

LDV是利用激光多普勒效应测量振动特性的一种非接触式实时测量仪器[11－12].实验采用的LDV工作距离为0.35～10m；速度量程为±50mm／s；振动速度的分辨率为0.1μm／s；最大线性误差为1.00%.采用LDV测量不锈钢条带的振动特性，激光测点位于被测条带的中心位置.LDV布置于被测条带的正前方，激光从LDV发出，经过空气、玻璃、水，到达被测条带的表面，发生反射后经由水、玻璃、空气，最后返回LDV.返回后的激光与入射激光的频率相差ΔfL，表达式为

图1 实验回路结构图Fig.1 Structural diagram of experimental loop

图2 实验段及不锈钢条带位置Fig.2 Test section and position of stainless－steel strip

式中：n为水的折射率；λ为入射光的波长.可通过式（1）获得不锈钢条带的振动速度

1.2 实验结果

当流速vf＝2.76m／s时，通过LDV测得的vs与时间t的变化关系时域图如图3（a）所示；经过Fourier变换获得其相应的频谱图，如图3（b）所示.由图3（b）可知，在该流速下不锈钢条带发生了共振，可以明显地观察到1 460Hz处的高频振动.当vf为0～6.0m／s时，条带涡激振动频率fv随vf的变化规律如图4所示.当vf为0.27～0.48，1.33～1.51，2.51～3.09，4.67～5.51m／s时，fv基本不随vf变化；当vf为0.50～1.27，1.56～2.24m／s时，fv与vf呈明显的线性关系；当vf为3.09～4.67m／s时，未在高频区域发现明显的峰值.

图3 当vf＝2.76m／s时条带振动时域图和频谱图Fig.3 Time domain spectrum and frequency spectrum of the strip at vf＝2.76m／s

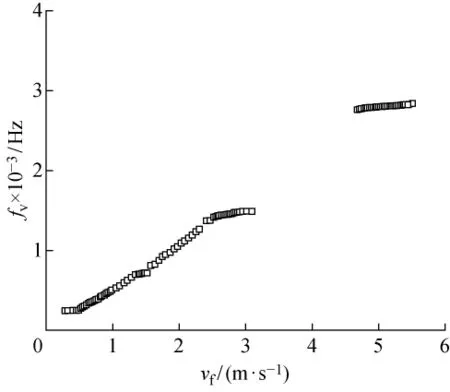
图4 fv随vf的变化关系Fig.4 Relationship between fvand vf

当vf为0.21～0.51，1.38～1.48，2.27～2.90，4.83～5.44m／s时的频谱瀑布图如图5（a）～（d）所示.fv被“锁定”在固有频率fn1＝253.9Hz，fn2＝710.4Hz，fn3＝ 1 460.0Hz，fn4＝ 2 804.0Hz附近，vs随着vf的增加呈现出先增加后减小的趋势.当vs达到最大时，fv与条带的固有频率fn一致，进而引起共振.当vf为0.56～1.27，1.56～2.30m／s时的频谱瀑布图分别如图5（e）和（f）所示.由图5（e）和（f）可知，除了由湍流激励激发的1阶固有频率fn1外，fv随着vf的增加而增加.而当vf为3.09～4.67m／s时，fv远离fn，此时无法引起条带的大幅振动.当vf为3.25～4.62m／s时的频谱瀑布图如图5（g）所示，未发现明显的高频振动峰值.这是由于随着fv的增大，结构高阶模态的刚度增强，测点处振动响应较弱所致.

绕流问题中通常采用Strouhal数（Sr）描述旋涡脱落的频率，其表达式为

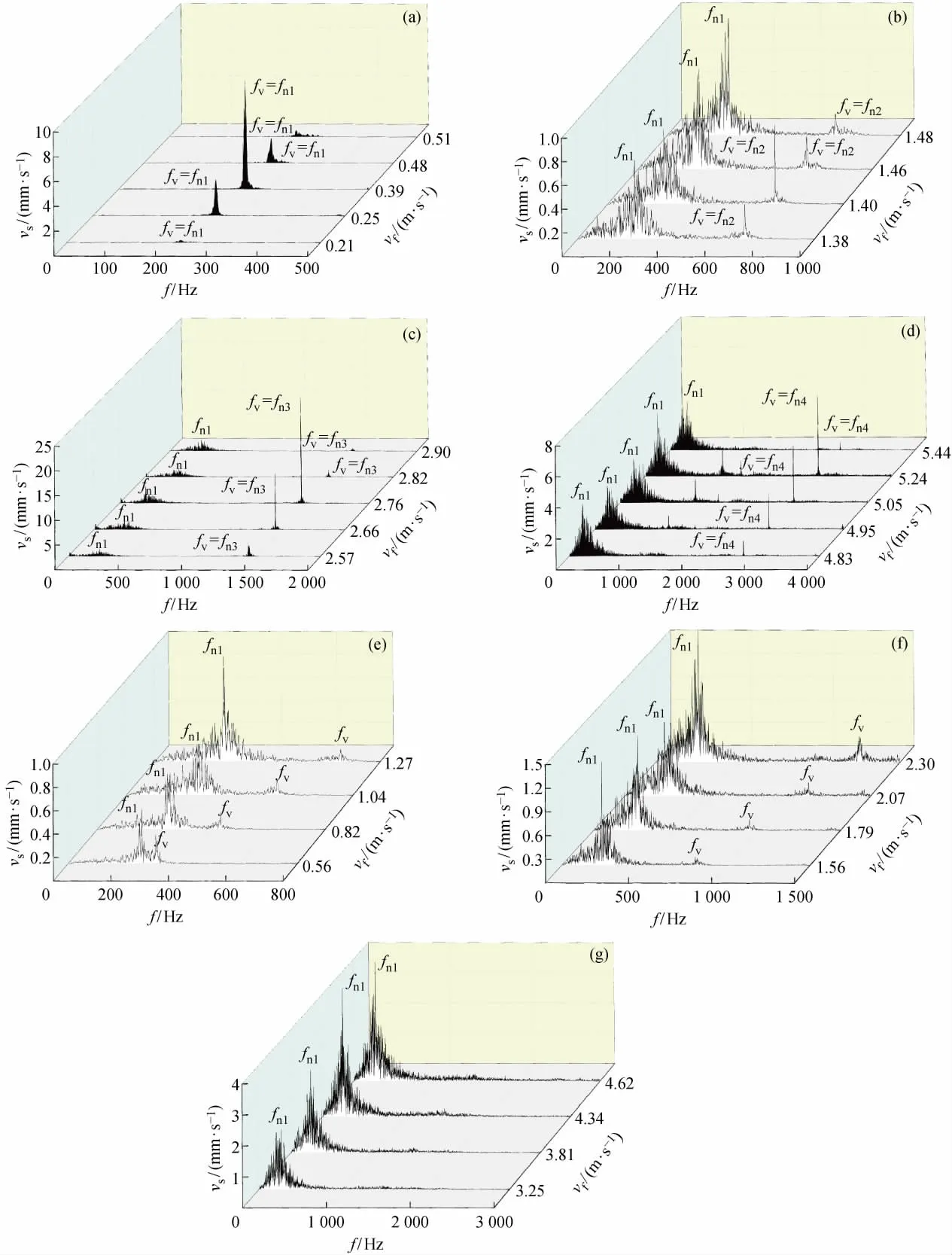
图5 不同流速下的频谱图Fig.5 Frequency spectrum of different straps

由fv计算得到的Sr与vf的变化关系如图6所示.由图6可知，在“锁定”区间内，fv基本保持不变，Sr随着流速的增加而减小；在“锁定”区间外，fv随着vf线性增加，Sr稳定在0.24左右.

图6 Sr随vf的变化关系Fig.6 Relationship between Sr and vf

2 模态分析

2.1 湿模态

模态分析通常在空气中进行，但空气密度较小，对计算结果的影响较小，故默认为在真空条件进行分析计算.对于受到液体作用的结构，由于液体密度比空气密度大，在进行模态分析时需考虑液体与固体之间的耦合作用.因此，将真空条件下进行的模态分析称为干模态分析，而考虑了液固耦合作用和液体附加质量效果的模态分析称为湿模态分析[13].

2.2 声固耦合算法

采用ANSYS声固耦合分析模块对平直条带进行湿模态分析.将流体所占据的空间区域视作声场区域；利用声学单元模拟流体；流固交界面满足“全沾湿、无滑移”假设，将处于流体与结构交界面单元的自由度完全绑定，以保证在振动过程中，边界上的流体与相邻结构的节点具有相同的法向速度，从而不会发生流体与结构的相互分离.根据Galerkin法及虚功原理[14－15]，能够分别获得声场有限元方程及结构有限元方程，将两组方程合并得到式（4），当给定流体材料的密度和体积模量时即可求解.

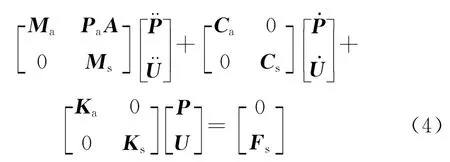
式中：Ma，Ca，Ka，A分别为声场的总体质量、阻尼、刚度矩阵以及耦合矩阵；Ms、Cs、Ks分别为结构的总体质量、阻尼、刚度矩阵；Fs为结构载荷矩阵；P为声压向量；U为结构位移向量.

在ANSYS分析模块中建立三维几何模型并划分网格，如图7所示.所建模型由66mm×10.6mm×0.46mm的不锈钢条带和66mm×12.6mm×12 mm包裹条带的水域组成，条带设置在水域中间位置.不同网格数量的网格敏感性分析如表1所示.由表1可知，不同网格数量对湿模态计算结果的影响较小，计算误差在0.5%以内，因此较少网格数量（序号1）即可达到计算要求.定义平直条带两端为固定约束；流体域为声场；声速为1 500m／s；求解算法为对称耦合；重力加速度为9.8m／s2；条带与水的接触面为流固耦合面.

图7 计算域设置Fig.7 Setup of computational domain

表1 网格敏感性分析Tab.1 Grids sensitivity analysis

2.3 计算结果分析

湿模态分析的计算结果如表2所示.表2中实验固有频率为平直条带各阶共振发生（振动速度vs最大）时对应的振动频率.由表2可知，ANSYS声固耦合分析模块能较好地模拟平直条带在水中的固有频率，1～4阶固有频率的模拟结果与实验值的偏差分别为2.9%、3.2%、6.6%和1.4%.

表2 模态分析结果Tab.2 Modal analysis results

3 结语

使用LDV测量窄矩形流道内，流动条件下水中不锈钢平直条带的振动特性.当vf为0.39，1.40，2.76，5.05m／s时，达到条带固有频率并发生共振；fn分别为253.9，710.4，1 460.0，2 804.0Hz时，在fn附近区域发生“锁定”现象；当vf为0.56～1.27，1.56～2.30m／s时，fv与vf呈明显的线性关系，Sr在0.24附近.采用ANSYS声固耦合分析模块对固有频率进行模态分析，计算结果表明：湿模态分析方法能较准确地模拟条带在水中的各阶固有频率.