节点本振误差对分布式发射波束形成性能的影响

袁 丁， 孙慧贤， 闫云斌， 全厚德

（陆军工程大学a.电子与光学工程系；b.无人机工程系，石家庄050003）

分布式发射波束形成（DTBF）利用多个分布式单天线节点，形成“虚拟天线阵”.各节点以不同的权值发射同一信息，形成定向波束指向接收端，所获得的定向功率增益可增强系统通信效能，包括扩展通信范围、提高通信速率、提升系统抗干扰能力等[1－2].DTBF在移动通信、无线传感器网络、电台应急通信等领域都有研究与应用.

DTBF要求各分布式节点精确同步载波信号[3].不同于集中式波束形成节点共用一个本振，每个DTBF发射节点配置有独立的本地振荡器产生载波信号.即使节点配置相同类型的本振，但由于制造工艺和外界环境温度等因素影响，节点本振输出会存在误差，进而影响DTBF合成性能.从本振输出的准确度和稳定度来看，本振误差包括载波初始相位偏移（IPO）、载波频率偏移（CFO）、相位噪声（PN）等3个偏差项.三者相互独立，且具有不同特性.因此，有必要分析不同本振误差偏差项对DTBF性能的影响.

已有研究多数采用接收端指标分析某一本振偏差项的影响.文献[4]分析了IPO对接收端误码率（BER）的影响，文献[5]选用接收信号强度（RSS）作为指标分析CFO影响，文献[6]则分析了PN对接收天线误差向量幅度（EVM）的影响.由于这些接收端性能指标存在阵列形式、信道条件、调制方式等适用场景限制，而且无法反映DTBF整体波束特征，文献[7]推导给出了任意阵平均波束图等指标，对DTBF性能进行了统计分析.而后，文献[8]基于平均波束图，分析了IPO对DTBF性能的影响.

目前，还少有文献分析同时存在以上3个本振偏差项时的DTBF性能.因此，本文建立了包含这3个偏差项的节点本振输出相位差模型，推导了存在本振误差时的任意阵平均波束图和互补累积分布函数的表达式，选用波束图参数指标，用以分析IPO、CFO、PN对DTBF性能的影响.

1 系统模型

1.1 DTBF系统

分布式发射波束形成系统如图1所示，N个发射节点任意分布在平面O－xy半径为R的区域，将发射节点i位置标记为（xi，yi），对应的极坐标为＝arctan（yi／xi）），i＝1，2，…，N.接收节点位于远场区，其位置坐标为（A，φ0，θ0），且有A≫ri.

为便于分析，进行系统假设[2]如下：

（1）假设节点位置固定，配置有单个全向天线，发射节点间隔足够远，可忽略节点天线耦合影响；

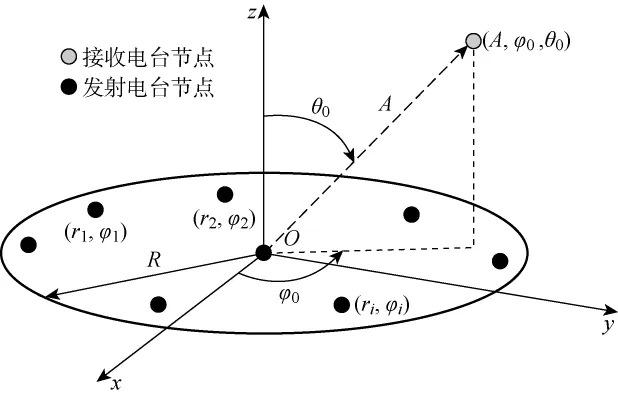
图1 DTBF系统示意图Fig.1 Diagram of DTBF system

（2）收发节点、发射节点间均为理想信道条件，不考虑信道存在散射、多径等情形；

（3）收发节点位置信息已知，已实现时钟同步和发射节点间发射信息共享.

为使DTBF合成波束指向目标方位（A，φ0，θ0），需合理设置各节点发射信号权重，调整节点发射功率和发射信号相位.为便于分析，设置发射节点辐射单位功率，且节点i发射信号相位为

1.2 节点本振误差模型

从本振输出的准确度和稳定度来看，本振误差包含载波初始相位偏移、频率偏移和相位噪声等3个偏差项.在影响分析时，考虑3个偏差项引起的本振输出相位差，建立如图2所示的节点本振输出相位差模型.

图2 节点本振输出相位差示意图Fig.2 Diagram of node oscillator output phase error

假设各节点配置同类型独立本振，且节点本振误差服从独立同分布（i.i.d），在图2模型及下述表述中，省略下标i.记Ts为符号时隙长度，在第m个时隙时刻mTs，节点本振输出相位差可表示为

式中：Δφp表示本振在初始时刻的随机相位差，IPO在初始时刻产生，且不随时间变化；Δφc（m）为CFO在mTs时间内累积的相位差，CFO反映本振输出的频率准确度，定义为本振实际输出载波频率fc与本振标称频率f0之间的差值Δf，其导致的相位差随时间呈线性增加，即 Δφc（m）＝2πΔfmTs；ΔφPN（m）为PN在mTs时间内累积的相位差.相位噪声表征本振输出的稳定度，假设PN在一个符号时隙内保持不变，在符号时隙与符号时隙之间发生变化，ΔφPN（m）为m个时隙累积PN之和，即ΔφPN（m）＝.第n个时隙（1≤n≤m）的PN为

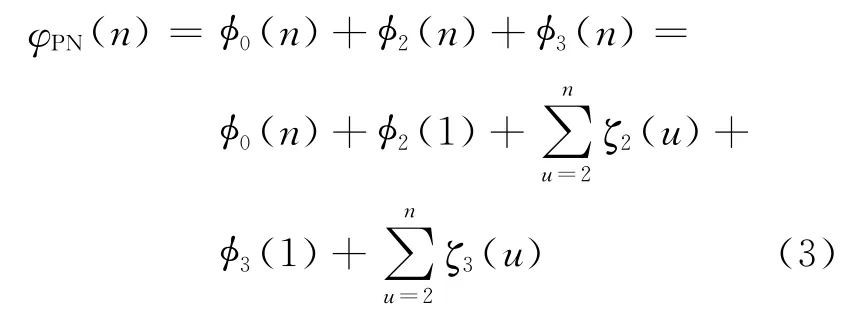
式中：φ0（n）为白噪声过程，为第n个时隙的白噪声累积量；φ2（n）和φ3（n）分别表示功率谱密度为1／f2和1／f3的色噪声过程[9]；φ2（1）和φ3（1）为对应的色噪声在第1个时隙的累积量，且有φ2（1）～N（0，.第u个 时 隙 （2 ≤u≤n）的对应色噪声累积量ζ2（u）≜ζ2（uTs，Ts）和ζ3（u）≜ζ3（uTs，Ts），且有

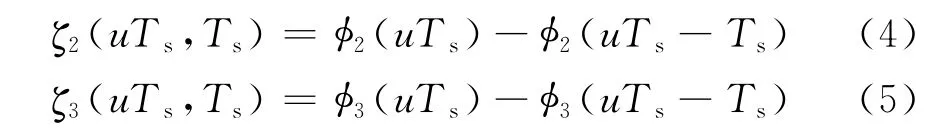
式中：ζ2（uTs，Ts）和ζ3（uTs，Ts）为零均值广义平稳（WSS）高斯过程.

PN多采用频域的功率谱密度来表征，对于白噪声和色噪声过程，其对应的功率谱密度（PSD）为

式中：K0，K2和K3为对应的相位噪声系数；γ为截止频率.

进一步地，可根据给定的噪声PSD，计算式（3）中φPN（n）的均值μφPN（n）和方差（n）为

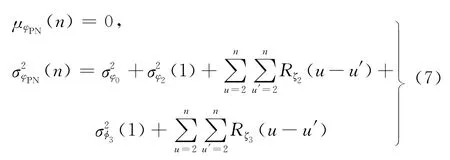
且有

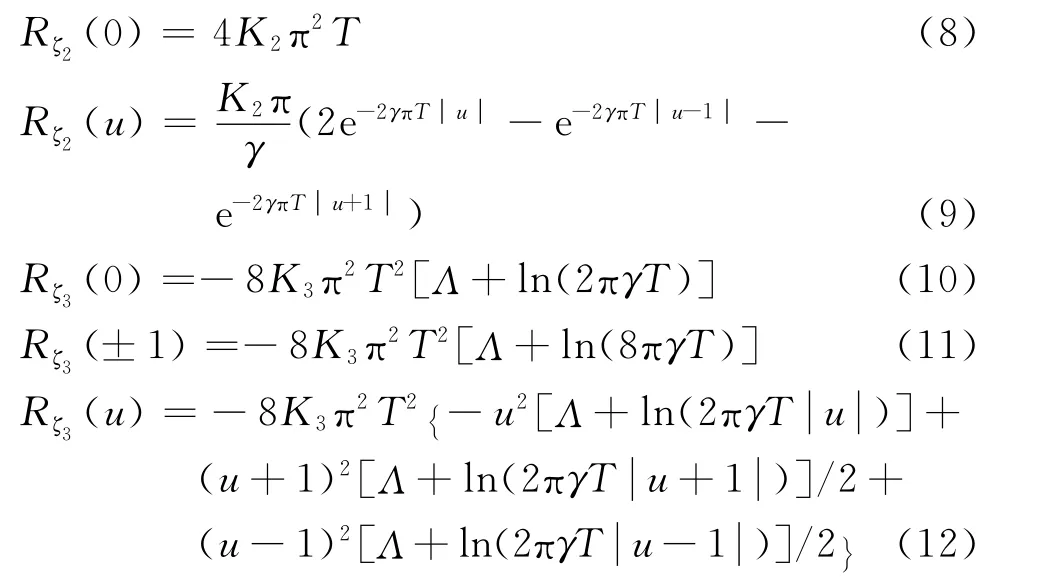
式中：Λ≜Γ－3／2；Γ≈0.577 2，为Euler－Mascheroni常量[10].

1.3 存在本振误差时的远场波束图

当存在本振误差时，节点i对应的发射载波信号相位变为此时，对应的“虚拟天线阵”的阵因子为

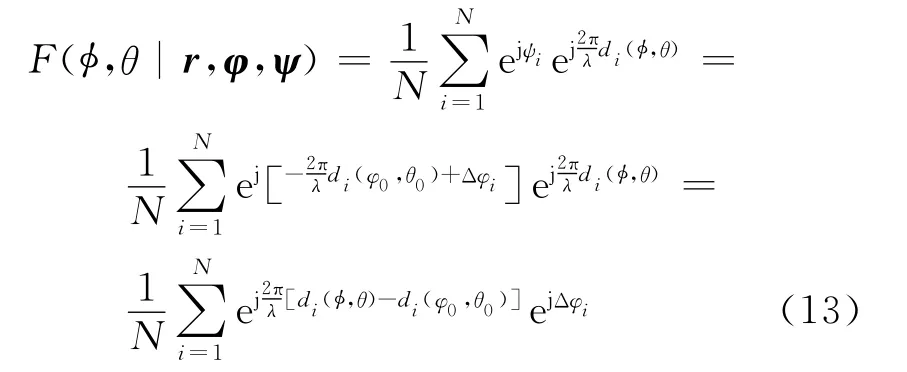
为描述“虚拟天线阵”在φ∈[－π，π）上的合成增益，定义远场波束图如下

2 本振误差影响理论分析

本节基于式（14）和（15），推导对应的平均波束图、互补累积分布函数（CCDF）表达式，对本振误差影响进行统计分析.

2.1 基于平均波束图的本振误差影响分析

式（15）包含变量zi和Δφi，考虑对远场波束性能进行统计分析.此时的平均波束图为

为求解上式，需要位置变量zi和本振误差变量Δφi的概率密度函数（PDF）.根据系统假设，节点服从任意分布，且节点本振误差随时间变化，无法事先假定其分布，此时的PDF求解问题转变为非参数估计问题.借鉴文献[7]和[11]，采用核密度估计（KDE）方法求解，可得在zi和Δφi处的核密度估计为

式中：在进行KDE时，采用了高斯核函数；h和s为核密度估计窗宽；M和K为核密度估计集的样本数；表示M个采样点的均值；表示K个采样点的均值.文献[11]讨论了KDE方法的适用范围和使用条件，证明了该方法适用于任意节点分布形式和任意节点数情形，且在足够的样本数下即可使核密度估计结果收敛于任意概率分布函数.核密度估计样本集可通过实际测量或经验模型获得.

将式（17）和（18）代入式（16）得

对式（19）进行化简得

对于式（20）等号右侧第二项，由核函数性质可知恒等于1，故上式可化为

同理，可化简式（19）等号右侧剩余项，则可得

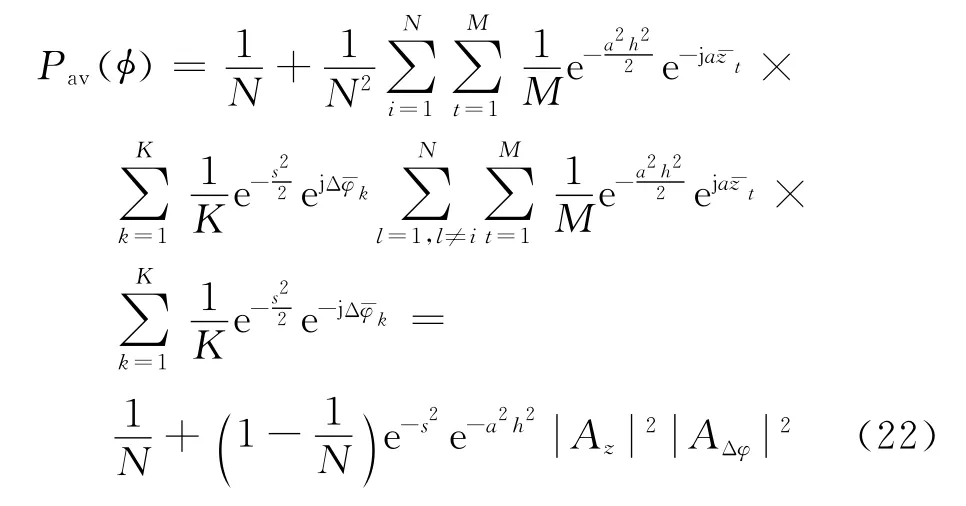
式中：等号右侧第一项表征平均旁瓣水平，第二项表征平均主瓣水平.存在本振误差时，主瓣表达式中增加了，平均主瓣水平发生变化.定义为衰减因子，且有即在没有本振误差时，误差越大则对应的衰减因子越小.对于AΔφ，当K足够大满足大数定理时，有AΔφ→由此可衡量本振误差对主瓣性能影响，当本振误差Δφ累积到40°时，DTBF主瓣性能会衰减到无本振误差情形的60%.由此，得到本振误差存在时的平均波束图的统一表达式.由于在推导过程中采用了核密度估计方法，所得表达式适用于任意节点分布和任意本振误差分布情形.

2.2 基于CCDF的本振误差影响分析

平均波束图Pav（φ）反映了远场波束图的统计平均特性，但某一任意阵形成的合成波束存在随机性，尤其是旁瓣水平会出现波动.定义CCDF来表征在任一角度φ的平均波束能量超过阈值P0的概率[11]，利用CCDF来分析本振误差对旁瓣的影响.将式（14）可变换为

式中：

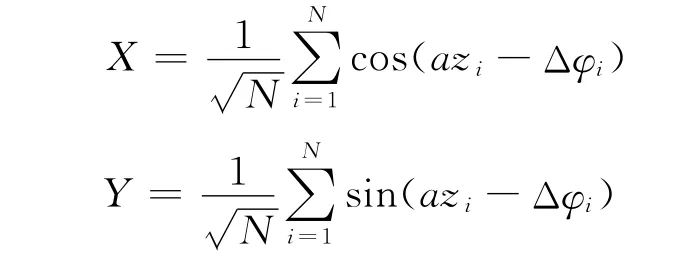
进而，存在本振误差时的CCDF可表示为

式中：

此时，求解CCDF问题转化为求解本振误差存在时X和Y的均值和方差.以X为例，其均值μx和方差σ2x可记为

为求解式（29）和（30），需要获得联合概率密度fi（zi，Δφi）.由于节点位置向量和本振误差向量相互独立，其联合概率密度分布函数可由KDE方法求解为

将式（31）代入式（29）和（30），可得

同理，可求得Y的均值和方差分别为

由此，即可求解某一角度φ处的CCDF，可见本振误差的存在改变了CCDF值，即改变了合成波束图出现阈值P0以上旁瓣的概率.

3 数值模拟

考虑发射端配置有单天线节点数N＝16，工作频率f0＝60MHz，对应波长λ＝c／f0＝5m.符号速率设置为4.8kbit／s，Ts＝1／4 800s.

设置节点分布在半径为R的区域，且服从Differential分布，该区域被等分为5个圆环区域，由内至外，每个圆环的节点数为总节点数N的29.55%，27.18%，22.41%，15.23%和5.63%，节点均匀分布在对应的圆环区域[7].模拟时，考察节点分布半径R＝15和75m这2种节点分布情形.

节点本振误差满足i.i.d分布，3个偏差项设置如下.

（2）频率偏移 Δf服从零均值高斯分布[12]，其标准差为σΔf＝f0×10－6，由其导致的相位偏差可根据式（2）计算得到.

（3）相位噪声.根据文献[13]，设置相位噪声PSD参数为：K0＝10－10，K2＝1.6和K3＝100，截止频率γ＝1Hz.

由于频率偏移引入的相位偏差和相位噪声随时间变化，所以考察初始（记为0）、Ts、5Ts、10Ts、15Ts等时刻的DTBF性能.模拟实验运行50次.

3.1 不同时刻平均波束图比较

图3给出了2种节点分布下的平均波束图，比较后可以发现：对于2种节点分布，节点分布半径越大，所得远场波束图的主瓣更窄.存在本振误差时，远场波束图的平均主瓣水平出现衰减，且本振误差越大，对应的平均主瓣水平衰减越大，波束形成的性能越差.

为进一步比较不同本振偏差项影响，分别定义衰减因子：本振误差衰减因子载波频率偏移衰减因子相位噪声衰减因子结果如表1所示.比较分析2种节点分布式情形结果，结论如下.

（2）对后续时刻，本振误差包含3个偏差项.频率偏移和相位噪声的加入，引起DTBF性能更大的衰减，对应，且随着时间增长，衰减因子逐渐减小.

图3 不同节点分布的平均波束图Fig.3 Average beampattern under different node distributions

表1 衰减因子比较Tab.1 Degradation factor comparison

3.2 波束图参数比较

在平均波束图基础上，进一步选取3个波束图参数以考察波束性能，其定义如下[13].

（1）3dB主瓣φ3dB，定义为φ3dB处波束增益比目标方向φ0衰减了3dB.波束合成设计时期望获得窄的主瓣，即φ3dB越趋向等于φ0，反映DTBF性能越优.

（2）3dB旁瓣区域S3dB，定 义 为S3dB≜且φsidelobe处波束增益比平均旁瓣水平高出3dB.平均波束图上会存在多个位置满足3dB增益要求，选取最小的角度值作为φsidelobe.波束合成设计时，希望减小旁瓣区域以使更多的能量集中在主瓣方向，即φsidelobe越大，反映DTBF性能越优.

（3）平均指向性因数，定义为聚集在目标方位能量与全域φ∈[－π，π）内总能量的比值，即有

3个参数的模拟结果如表2所示.从表2可以看出，节点本振误差也改变了波束图特性.随着时间的增长，本振误差逐渐累积，对应的波束图主瓣变宽，旁瓣区域扩展，平均指向性系数减小，波束图参数变化反映出DTBF性能的下降.尤其在15Ts时刻，出现φsidelobe＞φ3dB，即旁瓣区域覆盖主瓣，同时˜Dav＜0.2说明此时波束合成增益很小.

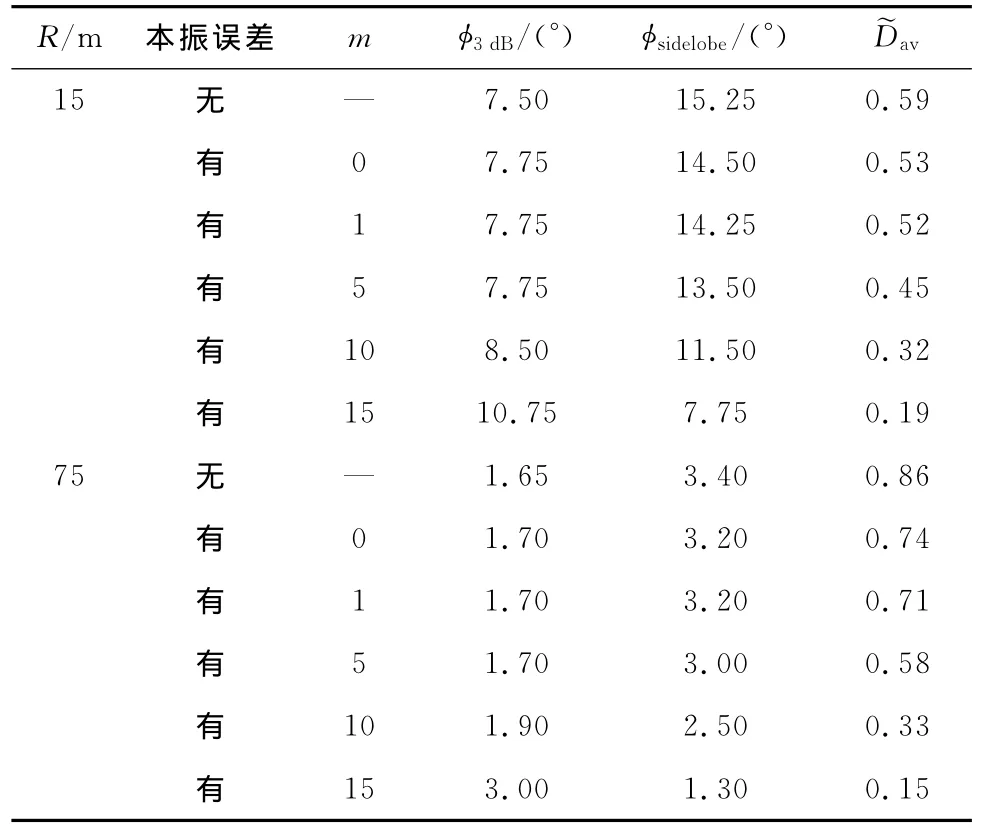
表2 波束图参数比较Tab.2 Beampattern characteristic parameters comparison

3.3 CCDF比较

CCDF反映本振误差对旁瓣区域的影响，由上文仿真结果可知，对任意节点分布，φ＝π／8始终位于旁瓣区域，故考察φ＝π／8，N＝16时，节点服从Differential分布，且半径分别为R＝15和75m时的CCDF，其仿真结果如图4所示.

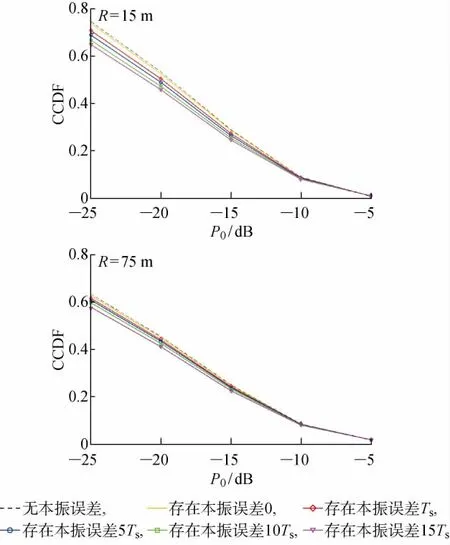
图4 不同节点分布的CCDFFig.4 CCDF under different node distributions

根据CCDF考察本振误差对旁瓣区域的改变，在进行DTBF设计时，期望获得低旁瓣.对于N＝16的DTBF系统，由式（23）可知，其统计平均旁瓣水平均为10lg（1／N）＝－12dB.对于2种节点分布情形，由图4结果可知，对于P0＞－12dB，所有情形对应的CCDF均小于0.2，说明系统出现对应功率值的旁瓣概率较小.但对于P0＜－12dB，存在本振误差时的CCDF小于无本振误差情形，说明存在本振误差时，系统出现对应功率值的低旁瓣的概率降低，旁瓣区域分布能量增多，也就意味着系统整体合成性能下降.

4 结语

本文分析了存在IPO、CFO、PN等3个本振误差项时的分布式发射波束形成性能，采用核密度估计方法，得到了对应的性能表达式.选用平均波束图、衰减因子、波束图特征参数、CCDF为指标，分析节点本振误差对DTBF性能的影响，并进行相关模拟分析，得到如下结论：

（1）本振误差会影响DTBF性能，其影响表现在两方面：① 影响远场波束图主瓣性能，导致平均主瓣水平下降，主瓣变宽；② 影响波束图旁瓣特性，本振误差会扩展旁瓣区域，并导致合成波束图出现高旁瓣.本振误差导致的主瓣和旁瓣特性的改变，使得聚集到目标方位的能量减少，且误差值越大，DTBF合成性能越差.

（2）这3个本振偏差项表现出不同的时间特性，其对分布式发射波束形成性能影响也是不同的.IPO初始时刻存在且不随时间变化，故在初始时刻DTBF性能的衰减是由IPO引起.CFO导致的本振输出相位差随时间呈线性增长，PN其所致相位差随时间累积，故CFO引起的性能衰减速度大于PN.时间越长，PN所致DTBF性能衰减越明显.