基于主成分分析的IPSO-SVM血泵转速预测

刘慧博 孟庆刚 任 彦

(内蒙古科技大学信息工程学院 内蒙古 包头 014010)

0 引 言

血泵对治疗心衰有着重要作用。心脏泵在人体内容易受到各种各样因素的影响，建立一种精度高的心脏泵转速预测模型对心脏泵病人具有特别重要的意义。文献[1]应用BP神经网络和遗传算法对血泵运行温度进行预测。文献[2]利用主动脉和左心室平均压差值,利用模糊PI控制器和动态自适应滑模控制器实现对血泵转速的控制。文献[3]将心脏的Frank-strarling定律使用在血泵控制器策略设计中。文献[4]通过神经网络最小滑模控制的方法对心脏泵的速度进行控制。文献[5]利用血泵得转速与功率特性曲线来对流量压力进行控制。文献[6]利用非参数模型自适应控制策略理论将心率和血流辅助指数作为模型控制变量，转速作为输出的控制策略，可以让心脏泵更好地适应体内的环境。文献[7]利用人群搜索-SVM对心脏生理参数进行预测研究。上述各类方法不能很好地适应血泵在循环系统中运行环境复杂性,难以应对各种不同状态，因此，本文提出了基于主成分分析的改进粒子群算法优化支持向量机建立预测模型的方法。

1 血泵与循环系统控制模型

在人体中血泵与循环系统构成了一个复杂的控制系统，血泵与循环系统构成的控制框图中，根据压力反射系统反馈的动脉血压，可计算循环系统的心率[8]。通过循环系统血流动力学特性得到主动脉血压、动脉血压、动脉血流量、静脉血流量、左心室压力容积、心率；然后对循环系统血流动力中心率、主动脉血压、动脉血压、动脉血流量、静脉血流量、左心室压力容积等七个因素进行主成分分析[9]，将第一、第二、第三成分作为输入，根据预测算法计算人工心脏泵的转速期望值；心脏泵驱动器将转速期望值作为控制输入，通过调整血泵驱动电压控制人工心脏泵转速。人工心脏泵的控制框图如图1所示。

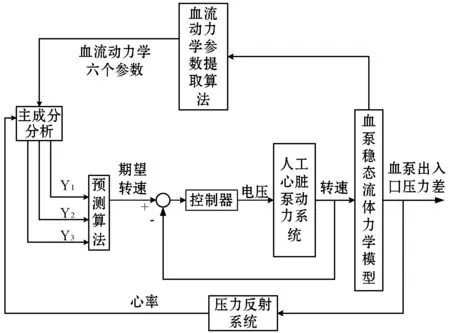
图1 血泵与循环系统控制框图

1.1 循环系统参数模型

循环系统集中参数模型包含左心房、左心室、体循环等三部分。模型中利用电压表示血压；利用电流表示血流量；利用电阻代表血管阻力；利用电容表示血管顺应性；利用电感表示血流惯性。简化后的循环系统集中参数模型如图2所示。图中各元件代表意义如表1所示。

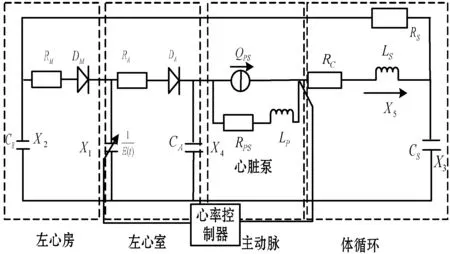
图2 血泵与循环系统电路模型

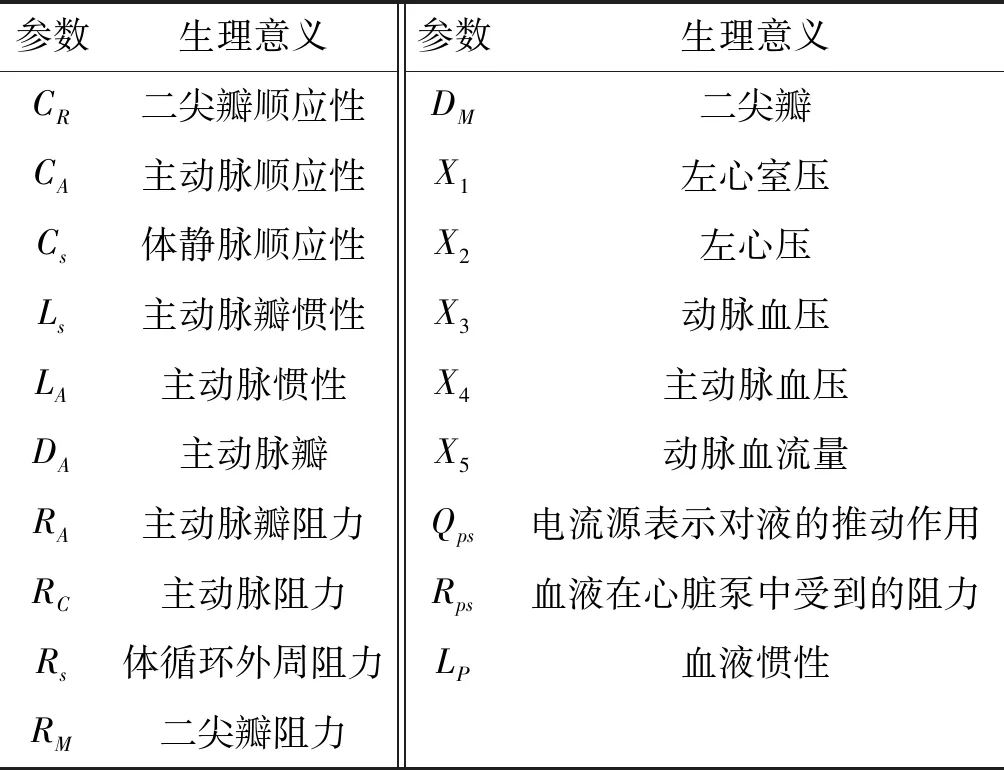
表1 电路模型各元件代表意义

从系统电路模型中可以得到心率、左心室压、主动脉血压、动脉血压、动脉血流量、静脉血流量。

1.2 心率与血泵转速关系

在血泵控制策略中，心率作为初始信号，直接反映心脏生理状态，利用心率与心输出量的函数关系、以及心输出量与人工心脏泵转速的函数关系，得到血泵转速期望值，根据人体具体需要进行转速调节,心率与转速的关系如图3所示。因此，心率是影响血泵转速的一个重要因素。

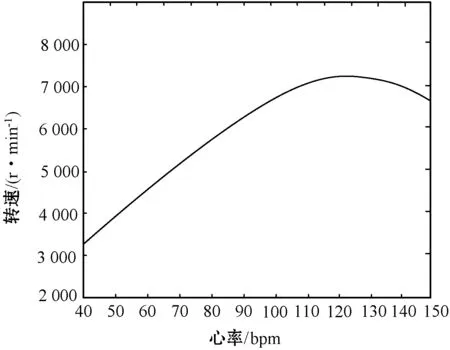
图3 心率与转速关系图

2 预测算法

由于循环系统中，影响血泵控制器转速期望值的过程参数较多，如果对得到的数据不加处理，直接将这些参数作为预测模型的输入变量，势必使得模型的输入变量过多，影响模型的预测精度。由此利用主成分对其中参数进行降维处理，简化预测难度，提高预测精度。

2.1 主成分分析的血流动力学特性降维

在血泵转速预测中，循环系统中的多个因素存在着很多的共性，因此循环系统中血流动力学因素选取了心率、左心室压、主动脉血压、动脉血压、动脉血流量、静脉血流量、左心室压力容积等七个因素，由于存在的参数太多，因此利用主成分分析法，降低模型输入维数，分析出血流动力特性的第一、二、三主成分[10]。

设观测到m维的数据样本矩阵为：

(1)

Step1求出矩阵的特征向量。

Step2获取相似系数矩阵:

(2)

式中:COV(X,Y)表示协方差；ρ表示相关系数。

Step3计算相关系数矩阵的特征值λi，特征向量为ei。

(3)

Step4求出主成分Yi。

Yi=e1X1+e2X2+…+emXi

(4)

式中:Yi表示第i个主成分。

Step5利用累计贡献率大于85%得出主成分数量。

(5)

式中:L表示前m个主成分的累计贡献率。

2.2 支持向量机模型的建立

SVM预测建模过程可以描述为：给定训练数据样本集{(xi,yj),i=1,2,…,l}，xi∈Rn且yi∈R，利用非线性的映射关系f在维度比较高的特征空间中建立线性回归关系：

f(x)=wT·φ(x)+b

(6)

式中：w表示权向量；φ表示非映射；b表示偏向量。

通过按照结构风险化最小的原则，得出：

(7)

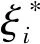
将问题转化成解决凸问题的优化，在此过程中，构造拉格朗日函数，求解为：

(8)

式中:K(xi,xj)表示核函数。

对上式加入高斯核函数，防止出现的映射为非线性的。得到回归函数关系式：

(9)

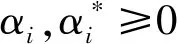
2.3 支持向量机血泵转速预测模型

血泵在病人体内运行过程中，受到体内复杂环境的影响，转速也会受到变化，当人的运动状态发生改变时，需要对血泵转速控制得更为精确，才能确保患者的正常生理活动，所以血泵转速的控制系统具有实时动态性，能在短时间内根据数据的变化对模型进行及时的更新。

原始支持向量机模型长时间工作后，其实效性会慢慢降低。若利用以前所有的数据进行建模，会大大增加模型的时间，对模型的实时控制达不到预期的效果。在此引入优化算法对SVM进行优化，解决了上述问题。此方法主要是通过改进粒子群算法对当前模型的工作过程中的参数进行优化，与之前得到的数据进行对比，得到比较相近的数据，然后通过建模的方式，估算出系统的输出。

2.4 改进粒子群算法

2.4.1标准粒子群算法

粒子找到两个极值后，通过下式不断更新自身速度和位置[11]：

(10)

(11)

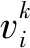
w=wmax-k(wmax-wmin)/Tmax

(12)

式中：wmax表示惯性权重最大值；wmin表示惯性权重最小值；k表示进化代数；Tmax表示设定的最大迭代次数。

2.4.2改进PSO算法

虽然标准PSO是基于调整惯性权重ω的自适应算法，能够很快找出局部最优解，但其寻找全局最优解的能力较弱。为了改进标准PSO算法的不足，本文利用动态的加速常数作为PSO的一种新的参数自适应策略。这种改进是在基本算法的基础上，实现c1和c2随进化代数线性的改变，即：

(13)

式中：R1、R2、R3、R4表示初始设定的定值；t表示当前进行代数；Tmax表示最大进化代数[12]。

2.4.3改进PSO算法优化SVM

将改进PSO算法中的粒子维度空间与SVM连接权值建立映射关系。改进PSO-SVM算法是采用改进PSO算法优化SVM的c和g等n个参数，将训练样本的个体对应的SVM预测误差作为个体的适应值，预测误差作为个体适应度值函数：

(14)

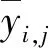
算法结束时，能寻找到全局最优点。在上述步骤基础上以最优点作为SVM初始值对网络进行训练，进而达到网络的训练目的。

2.4.4算法融合

改进PSO算法对SVM算法优化步骤如下：

(1) 初始化粒子维度D。PSO的粒子维度分量与SVM的连接值一一对应。

(2) 设置粒子的适应度函数，计算粒子的适应值。

(3) 利用改进的PSO算法优化SVM的c、g时等n个参数，并将优化后最优参数作为SVM的初始值，进行网络训练。

改进PSO算法优化SVM算法结构如图4所示。

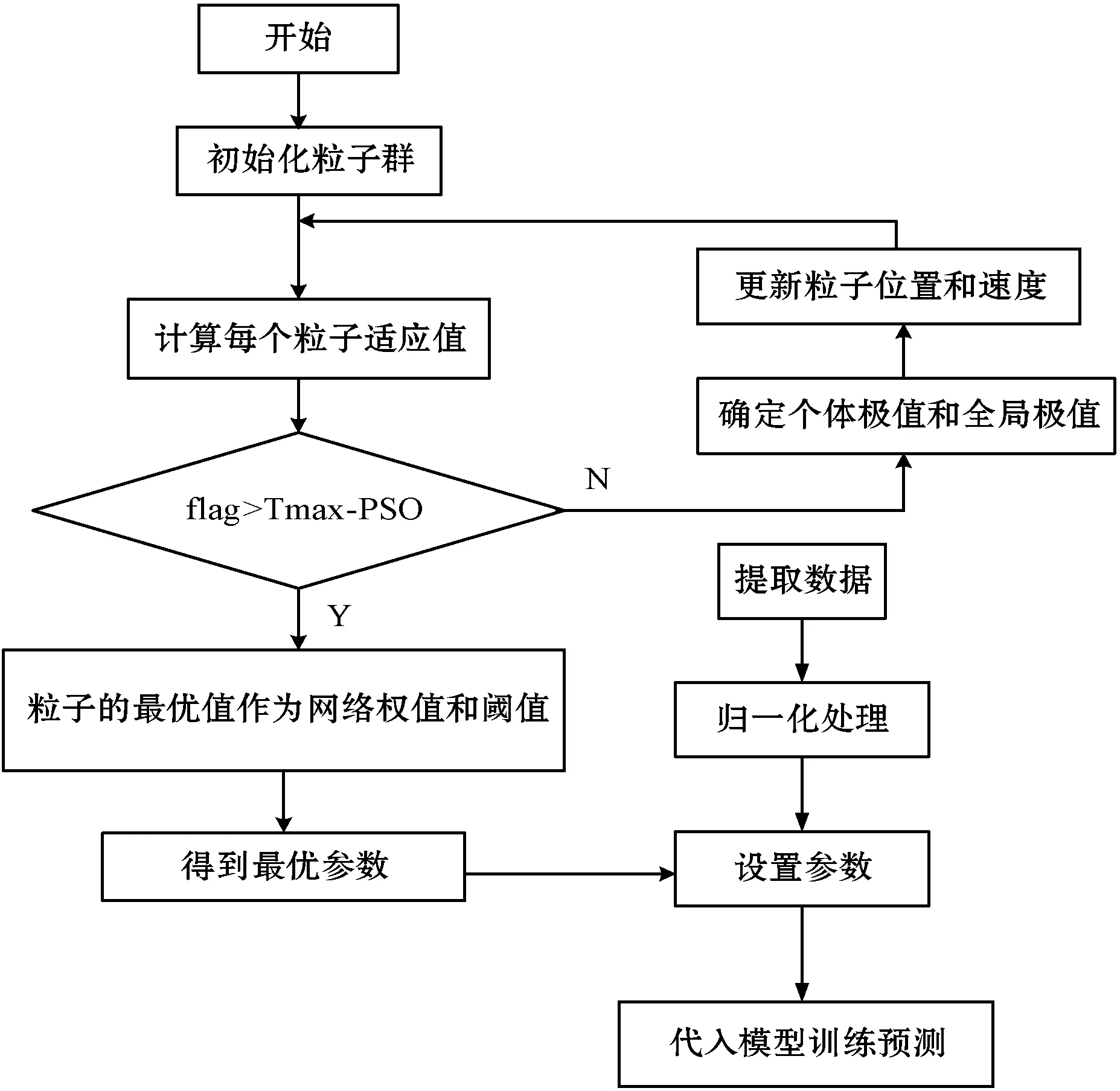
图4 改进PSO算法优化支持向量机流程图

3 血泵转速预测模型建立

3.1 数据选取

血泵在循环系统正常运行时，须满足人体在不同环境中对血泵期望转速值的需求。选取某医院病人血泵实际正常运行时的历史数据，四种状态休息、静坐、走路、轻微运动的实际转速，并得到所对应各个心室房压、血压、血流、心率等各个因素的60组历史数据。

3.2 PCA对数据处理

利用主成分分析对循环系统中血流动力学因素选取的七个因素进行降维处理，数据从循环系统所建立模型中获取，数据处理后结果如表2所示。

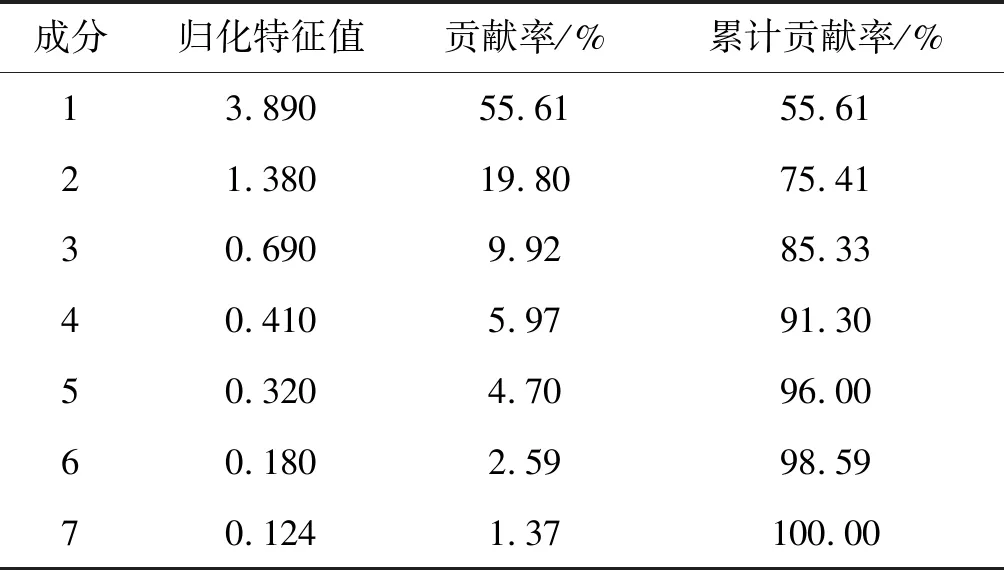
表2 特征值的贡献率和累计贡献率

通过对表2中的数据进行分析，得出前三个成分的累计贡献率达到了85.33%，已超过85%，因此选取前三个成分，对之前七个因素进行替换。前三个主成分的表达式如下：

Y1=0.39x1+0.35x2+0.37x3+0.37x4+

0.34x5+0.41x6+0.38x7

Y2=0.48x1+0.41x2-0.35x3+0.38x4-

0.43x5-0.20x6-0.28x7

Y3=-0.11x1-0.49x2-0.03x3+0.47x4-

0.50x5+0.07x6+0.50x7

式中:x1、x2、x3、x4、x5、x6、x7表示标准化后的心率、左心室压、主动脉血压、动脉血压、动脉血流量、静脉血流量、左心室压力容积。

根据上式可以得到不同转速各个主成分分析值。为了验证不同转速对应的各个参数特性，将所采集到的状态数据进行验证，符合循环系统要求。部分数据如表3所示。

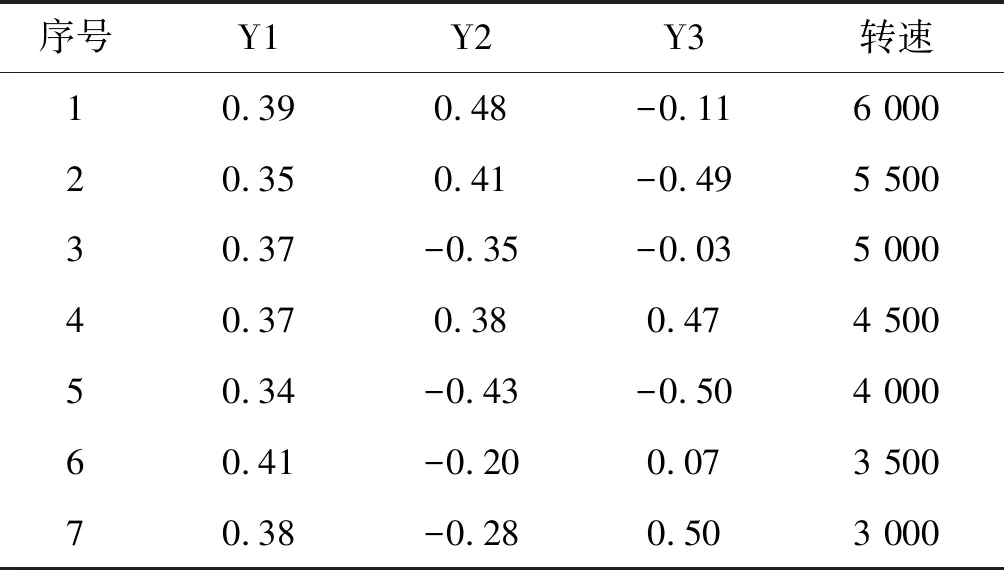
表3 降维后部分样本集

通过总成分分析和循环系统特性综合分析，再结合表3的数据处理结果，将Y1、Y2、Y3三个因素作为预测模型的输入。

3.3 改进PSO优化SVM模型

通过血泵在循环系统中运行期间，改进PSO算法优化支持向量机模型综合考虑到了工作过程中参数变化引起血泵期望转速的波动，因此预测模型精度有很大程度的提升。

通过选取血泵在体内的四种不同的状态，以及此时四种不同状态血泵控制器的转速期望值，将四种状态的期望转速设定为3 500 r/min、4 000 r/min、5 000 r/min、5 500 r/min进行仿真。

在模型预测中，将主成分分析的三个成分作为网络的输入，网络的输出量为血泵期望转速，模型的网络输入为3维，输出为1维，将前80%的数据作为预测模型的训练数据，后20%的作为输出数据。

3.4 仿真结果

在仿真中利用SVM模型类型s=4，核函数t=2，使用改进PSO算法优化支持向量机的惩罚参数c和核函数参数g时，以SVM模型样本均方误差作为目标函数，粒子群大小取为20，迭代次数k=160，c1=c2=2，惯性权重wmax=0.9，wmin=0.4，粒子速度最大值vmax=1，粒子速度最小值vmin=0.1。

利用MATLAB 2016a进行仿真，得到四种算法的收敛速度曲线如图5所示。

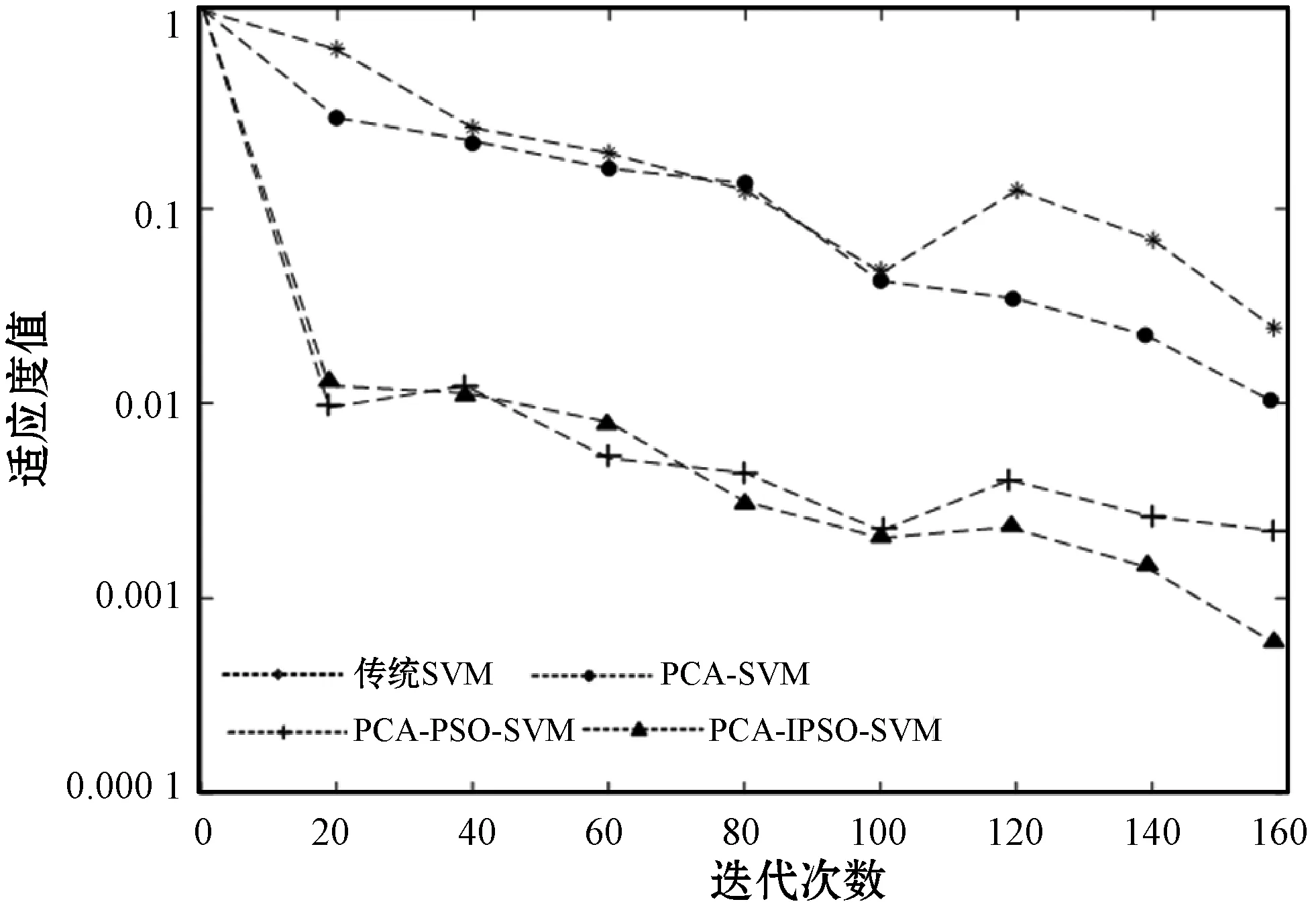
图5 算法的收敛曲线

从图5可以看出，算法运行初期，在初解解的精度方面，改进PSO-SVM高于传统SVM、PCA-SVM、PCA-PSO-SVM这三种预测模型。随着算法迭代次数增加，改进PSO算法选择策略显现出全局和局部搜索能力的优势，其收敛曲线下降速度加快，并最终收敛在最优解周围，而SVM和传统PSO-SVM算法收敛较慢，迭代次数完成时，会得到比较差的值。

应用改进PSO对SVM模型进行预测，在MATLAB 2016a平台下，预测模型的预测结果对比如图6所示。

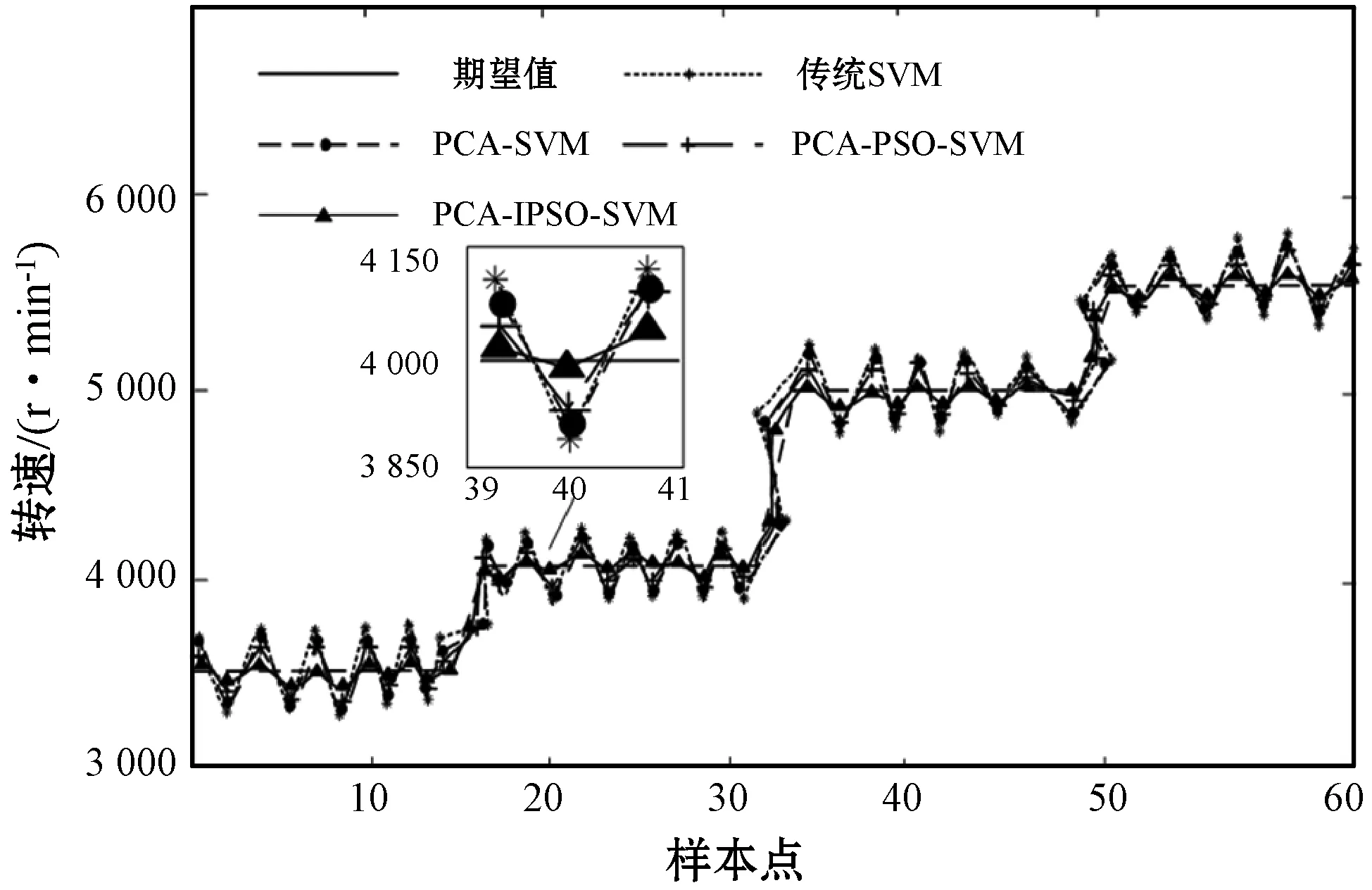
图6 血泵转速期望值预测图

由图6可以看出，本文提出PCA-IPSO-SVM算法比传统SVM、PCA-SVM和未改进的PSO-SVM预测值更接近血泵转速期望值，拟合的程度更好，预测模型的精度更加准确。

为了进一步验证本文提出预测模型的有效性和准确性，将本文改进PSO-SVM预测模型的结果与前人提出的传统SVM模型、未改进PSO-SVM模型进行对比，实验结果如表4所示。

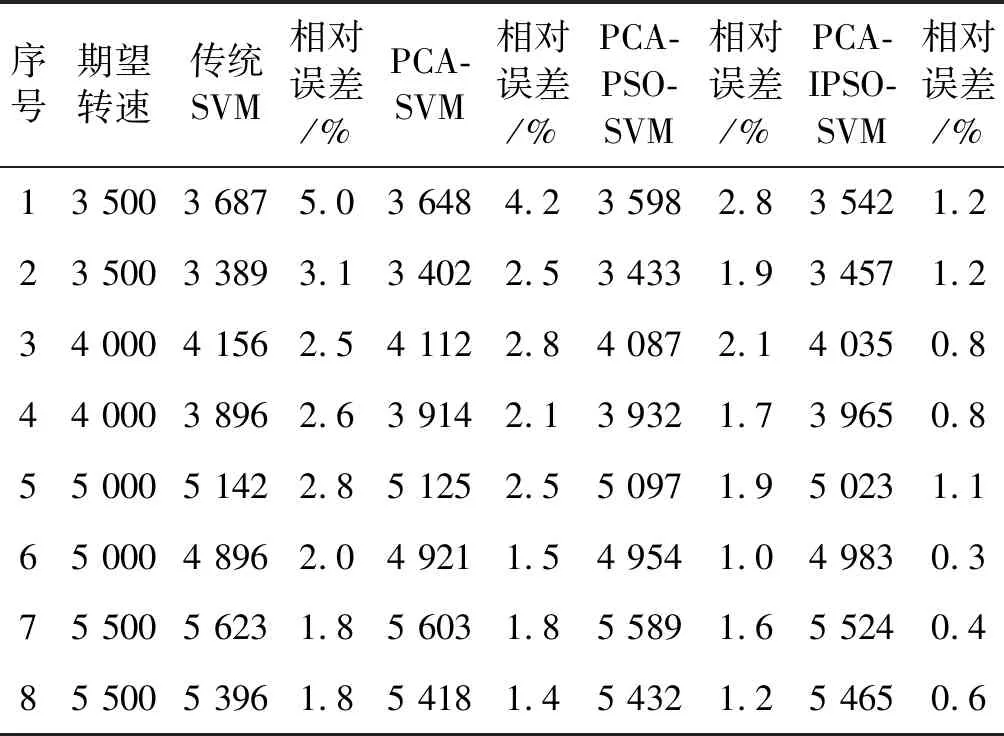
表4 三种模型部分实验结果对比

由表4可知，传统SVM预测模型的估计差值在100以上，相对误差较大；PCA-SVM与PCA-PSO-SVM模型的估计差值在100左右，相对误差较传统SVM模型有所降低，但仍在1%以上；PCA-IPSO-SVM模型的估计差值在50左右，相对误差基本小于1%，其预测精度优于前三种模型。

综上，改进PSO算法优化的PCA-SVM预测模型在理论上是可行的，能满足心脏泵运行过程转速精度要求。

4 结 语

本文提出了对血泵控制器期望转速预测的新方法，首先利用主成分分析对数据进行处理，然后利用改进PSO算法优化SVM模型，得到SVM模型最优值，最后对其预测模型的有效性和准确性进行了验证。实验结果表明，采用主成分分析的改进PSO算法优化的SVM预测提高了预测精度，说明了本文提出的PCA-IPSO-SVM预测模型是有效的。