还课堂片刻等待，听孩子解颐妙语

钱鸣

【摘  要】  以生为本就是要充分还原学生在课堂学习中的主体地位，主体地位的体现要充分体现出学生主人翁意识，还原学生深入课堂活动的时间和空间，这份时间来自于教师时间的还原，来自于思维时间和空间的保障。

【关键词】  主体;生态;课堂;初中数学

在初中数学的课堂教学活动中，我们如何做到主体地位的充分达成，笔者在此结合多年的教学经验和心得，总结如下几点：

一、深入研究学情，以学定教

有的放矢方能事半功倍，在教学过程中，我们首先要去深入了解学生的学情，锁定学生的学习态度、学习习惯、学习能力等方面，结合教学内容，预设好我们所教学生在这个环节可能遇到的难点和重点，预设好如何帮助学生突破这些重点和难点，也充分考虑好其中的策略，帮助学生搭建可以达到相应高度的脚手架、扶梯等。

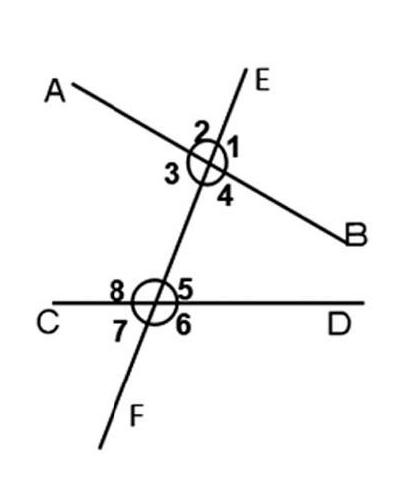
比如，在学习《探索两条直线平行的条件》的过程中，我们就要锁定本节课的重难点，此处的重难点就是掌握利用同位角相等、内错角相等、同旁内角互补判别直线平行的结论，并能解决一些问题。并思考其中的突破策略，比如，如何讓学生在体验中感悟利用同位角相等、内错角相等、同旁内角互补判别直线平行的结论是最为关键的，我们就可以利用如右图所示的图像，让学生观察右图并填空：（1）∠1与        是同位角;（2）∠5与∠3           ;（3）∠3与          是同旁内角。并结合已学的知识进行进一步提问如下两个问题：（1）内错角满足什么关系时，两直线平行？为什么？（2）同旁内角满足什么关系时，两直线平行？为什么？

以上就是学情的分析及其策略锁定，在这个环节我们定位精准了，才能做到有的放矢，才可能实现事半功倍。

二、充分还原课堂，以生为本

课堂中，我们必须给学生足够的思维空间和时间，那就要求我们在教学过程中还原课堂，还原课堂包括多个层面的还原，第一，是还原学生独立思考和互动交流的时间和空间，确保学生思维的充分性和深刻性。第二，是要为学生创设好值得思考的内容，让学生对思考的内容产生充分兴趣，这些兴趣一方面是迎合学生的喜好，另一方面要注重学生求知欲望的锁定。第三，在学生参与的过程中，教师并不是无事做，而是巡视课堂，结合学生的课堂表现进行适当的点拨、启发、激励等。在这样的三种前提下，我们才能实现学生课堂活动的真正还原，才能实现学生主体地位的真正落地。

比如，仍然以上面的《探索两条直线平行的条件》新授课教学为例，教师抛出问题：（1）内错角满足什么关系时，两直线平行？为什么？（2）同旁内角满足什么关系时，两直线平行？为什么？

然后我们应该从三步达成，第一就是给学生一定的独立思考，并启发学生从哪方面进行思考和分析，启发学生的思维方向，随后让学生以小组为单位进行交流互动，让学生基本能掌握相应的证明方法，第三步就是请学生上来展示自己交流的成果，学生在展示的过程就是一个再思考的过程，这个过程能充分考虑到学生对问题的再思考、再分析，最终还要用自己的语言表达出来，一来二去，学生的学习能力、表达能力等都得到了充分提升。

在这个环节，我们教师一定要改变传统的观念，要善于把自己的角色进行转变，要让学生实现主体地位的达成和提升。

三、巧妙循序渐进，逐渐提升

任何知识与技能的建构与提升都是有一个循序渐进的过程的，教师在备课的过程中，主要不是考虑我能给学生多少，而是我们的学生在课堂中能接受多少，怎么接受才能提升他们的接受效率，提升学生对数学内容的理解深度和广度，并促进学生在学习过程中学科关键能力的提升，比如分析能力、数学结合能力、阅读能力等等。因此，在这个环节中，我们需要换位思考我们的教学内容，并结合教学内容锁定循序渐进的内容及其实施策略。

比如，在中考复习过程中，我们会遇到直角三角形共斜边模型，这种模型是辅助圆中最为常见的一种，在此，笔者教学中就通过以下三步实现循序渐进。

第一步模型解读如图所示，呈现两种模型的本质。

第二步模型分析，如上图所示，模型的本质是：（1）共斜边的两个直角三角形，同侧或异侧，都会得到四点共圆;（2）四点共圆后可以根据圆周角定理得到角度相等，完成角度等量关系的转化，是证明角相等重要的途径之一。

第三步建模模型实例，为了让学生进一步理解直角三角形共斜边模型在解题过程中如何用好辅助圆，我们可以列举以下两题，由浅入深、由点及面。

例1.如图，AD、BE、CF为△ABC的三条高，H为垂心，问：

（1）图中有多少组四点共圆;

（2）求证：∠ADF=∠ADE。

例2.如图，E是正方形ABCD的边AB上的一点，过点E作DE的垂线交∠ABC的外角平分线于点F。求证：EF=DE。

通过这两题的分析，一切就顺其自然的，由此可见，这样的教学真正实现了生本课堂，还原了课堂的生态，促进了学生的生长。

〔备注：本文系江苏省教育科学“十三五”规划专项课题《生态教育视域下初中课堂候答实践研究》的理论研究成果之一（E-b/2020/14）。〕