基于ANSYS软件的农用车车架静强度有限元分析

李 军,周敬勇,李 勇

(合肥职业技术学院 汽车应用与轨道交通学院，安徽 合肥 238000)

农用车车架在行驶过程中不仅要承受来自发动机总成、驾驶室和货物等物体的载荷，还要承受不平路面施加的强制位移载荷，导致了各种力和力矩同时作用在车架上。因此，车架必须具有足够的刚度和强度，否则将引起车架变形过大从而导致大梁开裂或断裂，引起严重的交通事故。要保证车架拥有足够的刚度与强度，就必须对其进行静力学分析，校核车架在多种典型工况下的静强度，并为结构优化设计提供依据。本文利用ANSYS软件对农用车车架进行弯曲、扭转和刹车工况进行静力学分析，研究车架的静强度性能。

1 有限元静力学分析的理论基础

1.1 静力学分析的基本理论及流程

结构静力学分析是研究在不随时间变化的恒定载荷作用下系统的响应，如结构的位移形式、应变、应力分布和约束反力等参数。在结构静力学分析中不考虑系统的质量和内摩擦特性，所以可以忽略惯性和阻尼效应作用在结构上的位移、力、应变和应力。实际上，不随时间变化的恒定载荷是一种理想的假设，随时间缓慢变化的载荷也属于恒定载荷，如近似静力载荷。在有限元结构静力学分析中，施加的外部载荷一般有集中力、分布压力，而内部载荷则往往是重力和离心力，另外还有一种载荷称为位移载荷，如地面对车架的强制位移载荷。[1]有限元静力学分析主要是基于弹性力学理论，从静力学、几何学、和物理学三方面来研究结构的特性，通过平衡微分方程、几何方程、物理方程和边界条件来推导结构内部的内应力分量与体力、面力之间的关系式，应变与位移之间的关系式以及应变与应力之间的关系式。上述提到的三种关系式对应的方程分别是：平衡方程、几何方程和物理方程。

平衡方程。当结构在外力作用下处于平衡状态时，平衡方程为：

几何方程。在忽略位移导数的高次项后，描述应变与位移关系的几何方程为：

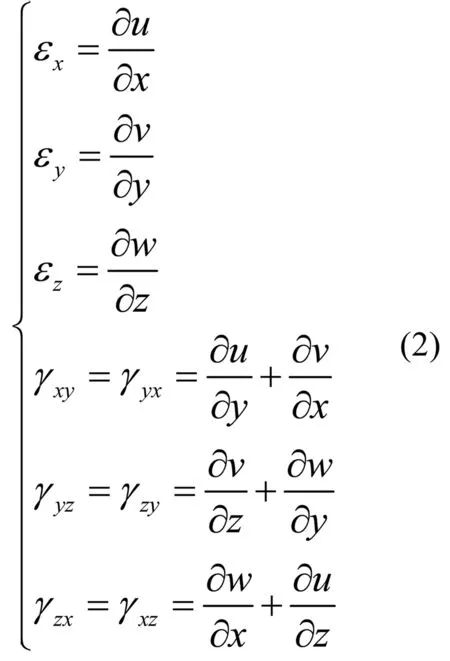
物理方程。在线性弹性有限元分析中，描述应变与应力之间关系的物理方程为：

综合上述的平衡方程、几何方程和物理方程及边界条件，有限元分析中的静力学基本方程可以描述为：

式(4)中，K是结构的总体刚度矩阵；U是位移列向量；F是载荷列向量。总体刚度矩阵K是由单元刚度矩阵组成，位移列向量U是由个节点位移组成，载荷列向量是作用在单元节点上力的集合。

有限元结构静力学的分析流程如图1所示，具体步骤为：

(1) 单元分析。单元分析的主要任务是通过引入位移函数来描述单元内部任意点的位移与节点位移的关系，进而推导单元节点力与节点位移的关系，得到单元刚度矩阵。

图1 结构静力学分析流程

(2) 整体分析。将各单元的单元刚度矩阵按照一定规律进行组合就得到结构的总体刚度矩阵，从而建立起整个结构的节点载荷与节点位移之间的平衡关系。

(3) 约束分析。约束分析是将研究对象的边界条件引入，消除刚度矩阵的奇异性，为计算求解做准备。

(4) 静力学分析-方程求解。根据已知的整体刚度矩阵和外载荷列向量，对式(4)进行求解，获得整体结构的位移列向量。

(5) 单元节点力、应力和应变的计算。根据节点位移来计算单元节点力、应力和应变。

(6) 结果后处理。通过结果后处理来显示结构的应变、应力云图，以及获得响应关键点的最大值和最小值，为结构的强度、刚度校核提供参考。

1.2 等效应力理论

第四强度理论(又称为畸变能理论)认为畸变能密度的变化会引起材料发生屈服，微小单元内的均方根剪切力的大小是衡量材料破坏与否的重要因素，只要微小单元内的均方根剪切力超过一定值，材料就会发生屈服现象，继续增大剪切力就有可能导致材料发生断裂。

农用车车架是一个复杂的机械结构，为了保证车架能实现基本功能，其结构本身必须具备足够的刚度和强度，否则将导致严重的交通事故。农用车车架一般是由钢板焊接或铆接而成，材料的失效一般是以发生塑性变形为标志，因此可以根据第四强度理论对农用车车架的静强度进行校核。

AYSNS软件遵循材料力学第四强度理论，依据等效应力(Von Mises应力)来判断农用车车架的强度是否满足使用要求。等效应力的计算公式为：

式(5)中： σr是等效应力；σ1是第一主应力；σ2是第二主应力；σ3是第三主应力。屈服强度判断准则为：

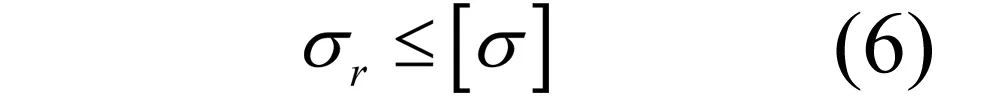
式(6)中： [σ]是材料的许用应力。

由式(6)得知，当农用车车架的等效应力大于材料的许用应力时，车架钢板发生屈服变形。

2 农用车车架的静强度工况分析

农用车在行驶过程中承受多种类型的载荷，较为典型的是弯曲载荷，扭转载荷、拉伸载荷、横向载荷和纵向载荷[2]。农用车在平整路面行驶时受到的弯曲载荷主要由货物、车身、车载设备、乘客和各种零部件的重力引起，车架在弯曲载荷作用下呈现出弯曲变形形态。当农用车在不平路面行驶时，车轮在障碍物作用下抬升，进而给车辆悬架系统施加路面激励，实质是给车架施加强迫位移激励，导致扭转载荷的产生，具体表现形式为前轮悬空。农用车遇到紧急情况进行急刹车时，由于车辆本身和货物的巨大惯性，导致车架承受极大的惯性力，很可能引发局部应力集中从而破坏车架的正常形态，因此在车架的静强度校核中需要深入分析[3]。

本文根据农用车的实际作业环境和车架的结构形式，利用ANSYS软件对农用车车架的三种典型工况进行静力学分析，用以校核农用车车架的静强度。三种典型工况分别是：满载弯曲工况、满载扭转工况和满载紧急制动工况。上述三种工况基本覆盖了农用车使用过程中的车架破坏形式，分析结果可以为企业提供车架改良依据。

满载工况各部分载荷分别是：货物重量为59950N，动力总成重量是6500N，驾驶室和乘员总重为7800N。

2.1 满载弯曲工况

满载弯曲工况是模拟农用车载满货物下在平整路面正常行驶的工况，该工况下农用车的四轮同时着地、行驶路线为直线。在实际行驶过程中，农用车不可能行驶在绝对平整的路面，不平路面会造成农用车竖直方向的附加加速度，路面越颠簸，附加加速度越大，附加载荷越大，农用车的行驶环境越恶劣。静强度校核的目的是要充分考虑农用车在最恶劣工况下的强度性能，因此在进行满载弯曲工况分析中需要把不平路面引起的附加载荷考虑进去[4]。在ANSYS静力学分析中，通常用动载系数代替负载载荷。动载系数与路面条件、车辆行驶状况和车辆结构系统(如悬架系统)有关。为了简化分析过程，根据经验和半经验公式，本章的农用车车架满载工况计算中取动载系数为3。

(1) 约束条件

在车架满载弯曲工况分析中，约束条件为：约束左、右前轮板簧处节点的3个平动自由度(UX、UY、UZ)；释放左、右前轮板簧处节点的3个转动自由度(ROTX、ROTY、ROTZ)；约束左、右后轮板簧处节点的竖直方向平动自由度(UY)；释放左、右后轮板簧处节点的2个平动自由度(UX、UZ)和3个转动自由度(ROTX、ROTY、ROTZ)。

图2 弯曲工况下车架的位移云图

(2) 计算结果及讨论

图2给出了满载弯曲工况下农用车车架的位移云图。从图2中可以看出，弯曲工况下车架的最大位移为1.026 mm，最大位移发生在安装发动机总成的第一根横梁处；中间的第2、3根横梁的变形达到0.684 mm，所以车架变形呈现为U型；两根纵梁的边上也出现的较大的变形，几乎达到0.798 mm。

图3 弯曲工况下车架的应力云图

图3给出了满载弯曲工况下农用车车架的应力云图。从图3得知，农用车车架的最大应力为97.421 MPa，最大应力出现在第一横梁处；纵梁边缘处也存在较大的应力，基本达到75.772 MPa。

从图2和图3可知，满载弯曲工况下农用车车架的位移和应力都没有超出许用范围(许用应力为230 MPa)，最大应力只有97.421 MPa。

2.2 满载扭转工况

农用车行驶在不平路面时，路面上的障碍物会将一侧的车轮抬高，在这过程中路面将给农用车施加一个较大的扭转力矩，在扭转力矩的作用下车架将发生扭转变形，若变形幅度较大，车架很可能发生塑形变形导致无法正常工作[5]。因此，必须在满载扭转工况下对农用车车架进行强度校核，以保证车架具备足够的强度性能。

图4 扭转工况下车架的位移云图

(1) 约束条件

在车架满载扭转工况分析中，约束条件为：约束右前轮板簧处节点的3个平动自由度(UX、UY、UZ)；释放右前轮板簧处节点的3个转动自由度(ROTX、ROTY、ROTZ)；释放左前轮板簧处节点的所有自由度；约束左、右后轮板簧处节点的竖直方向平动自由度(UY)；释放左、右后轮板簧处节点的2个平动自由度(UX、UZ)和3个转动自由度(ROTX、ROTY、ROTZ)。

在满载扭转工况计算中，给左前轮板簧处节点施加一个20 mm竖直向上的强迫位移，用以模拟障碍物将左前轮的抬升[6]。

图5 扭转工况下车架的应力云图

(2) 计算结果及讨论

图4给出了满载扭转工况下农用车车架的位移云图。从图4可以看出，满载扭转工况下车架的最大位移发生在左纵梁与第一横梁交接处，最大变形值达到2.369 mm，且车架呈现出不对称扭转变形。

图5给出了满载扭转工况下农用车车架的应力云图。从图5可以看出，车架的最大应力达到175.321MPa，最大应力出现在第一根横梁处；梁纵梁的边上也出现较大的接触应力，达到155.841 MPa。

通过图4与图5得知，满载扭转工况下车架的最大应力为175.321MPa，没有超出材料的应力极限。

2.3 满载紧急制动工况

农用车在行驶过程中遇到突发事件时需要紧急制动，由于农用车载货量和车身重量较大缘故，使得紧急制动工况下车架容易出现开裂甚至断裂[7]。因此，在满载紧急制动工况下有必要校核农用车的车架强度。在紧急制动工况中，给车架施加一个大小为10 m/s2的纵向加速度，用以模拟紧急制动时所附加的惯性力。

(1) 约束条件

在车架满载紧急制动工况分析中，约束条件为：约束左、右前轮板簧处节点的3个平动自由度(UX、UY、UZ)；释放左、右前轮板簧处节点的3个转动自由度(ROTX、ROTY、ROTZ)；约束左、右后轮板簧处节点的竖直方向平动自由度(UY)和纵向平动自由度(UZ)；释放左、右后轮板簧处节点的1个平动自由度(UX)和3个转动自由度(ROTX、ROTY、ROTZ)。

图6 紧急制动工况下车架的位移云图

(2) 计算结果及讨论

图6给出了满载紧急制动工况下农用车车架的位移云图。通过图6可知，紧急制动工况下车架的最大位移出现在第一根横梁处，达到5.837 mm；除此之外还可以看到车架尾部的变形也较大，原因是货物的惯性力较大。

图7给出了满载制动工况下农用车车架的应力云图。从图7可以得知，紧急制动工况下车架的最大应力出现在纵梁和第一横梁连接处，应力值达到372.654 MPa；悬架与车架连接的螺栓孔也存在较大的应力，几乎达到207.03 MPa。

图7 紧急制动工况下车架的应力云图

从图6与图7可知，紧急制动工况的最大应力为372.654 MPa，已远远超出材料的许用应力(230 MPa)。因此在车架的结构优化设计阶段需要重点关注紧急制动工况下车架的应力集中现象。上表给出了农用车车架在满载弯曲工况、满载扭转工况和满载紧急制动工况下的最大位移与最大应力。可以看出，最大位移和最大应力都出现在满载紧急制动工况。因此，满载紧急制动工况是最容易造成车架损坏的工况，需要密切关注[8]。

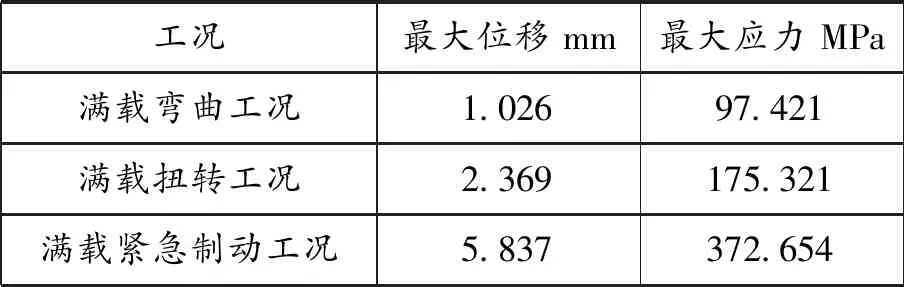
最大位移与最大应力表

上表给出了农用车车架在满载弯曲工况、满载扭转工况和满载紧急制动工况下的最大位移与最大应力。可以看出，最大位移和最大应力都出现在满载紧急制动工况。因此，满载紧急制动工况是最容易造成车架损坏的工况，需要密切关注[8]。

3 结语

本文首先介绍了平衡方程、几何方程和物理方程，在融入边界条件后得到了有限元静力学理论的基本方程。然后详细描述了有限元结构静力学的分析流程，并对等效应力概念和公式进行了解释。之后根据农用车的行驶环境和结构特点 ，在满载弯曲工况、满载扭转工况和满载紧急制动工况下对农用车车架进行了静力学分析，得到了三种典型工况下的位移分布云图和应力分布云图，为农用车车架的结构优化提供了可靠的依据。