基于空洞卷积神经网络的金刚石图像语义分割*
潘秉锁, 潘文超, 刘子玉
(中国地质大学(武汉) 工程学院, 武汉 430074)
金刚石颗粒的粒径、椭圆度、圆度等形状特征参数是金刚石质量对比的重要依据,也是金刚石分级和选用的基础[1]。而在金刚石工具的使用过程中,金刚石的出刃状态是工具性能、加工对象特性及操作规程的综合反映。获取出刃金刚石的形态参数是分析金刚石工具加工性能的基础[2]。因此,研究金刚石颗粒的形状表征方法,具有重要意义。
随着计算机技术和数字图像处理技术的发展,已有不少关于以数字图像处理技术为基础的金刚石特征参数测量方法的报道。JIANG等[3]采用机器视觉系统和最大类间方差阈值法(Otsu法)分割了金刚石锯片刀头的数字图像,进行了金刚石出刃率的测量。史长琼等[4]以Canny算法为基础,采用动态阈值进行了金刚石颗粒图像的边缘检测,从而实现了金刚石粒径的自动测量。王庆海[1]以HALCON为平台,采用阈值法进行了金刚石颗粒彩色图像的分割,测量了金刚石粒径、圆度、椭圆度、净度、形状等特征参数。江国学等[5]基于Matlab的图像处理工具箱,对金刚石微粉的数字图像进行了图像增强和阈值分割,提取了金刚石颗粒图像并测量了颗粒数目、面积等参数。潘秉锁等[2]针对孕镶金刚石钻头唇面图像的颜色特征,采用模糊聚类方法对图像中的金刚石颗粒进行了分割,取得了较好的分割效果。龚俊锋等[6]采用动态轮廓模型对金刚石的融合图像进行了分割,得到了完整连续的金刚石颗粒轮廓。这些工作为金刚石颗粒和金刚石出刃形貌的自动分析打下了良好的基础。但由于金刚石是透明材料,获取的金刚石颗粒图像往往存在背景颜色不均匀、金刚石颗粒与背景边界不清楚、金刚石侧晶面或其他局部区域因光照角度而过于光亮等问题。这些问题对于目前以阈值分割为基础的金刚石颗粒提取方法而言,是很大的挑战。
近年来深度学习在图像分割和图像识别等领域取得了很大的进展,在医学、生物、自动驾驶等领域取得了较好的应用效果[7-9]。基于深度学习的语义图像分割不是单独进行复杂的特征提取,而是构造含有大量参数的深层神经网络,通过网络训练,自动提取图像特征。由于网络训练是一种有监督的学习过程,所训练的分割模型能够在像素级别上对一幅图像中的每个像素点进行语义归类。因此,在一定程度上它可以克服传统图像分割方法在分割过程中受参数影响大、对噪声敏感、分割准确度不高等缺点。
针对金刚石颗粒数字图像处理中存在的图像分割难题,采用空洞卷积神经网络对金刚石颗粒图像进行语义分割,研究批处理规模、卷积层卷积膨胀系数、过滤器数量等超参数对金刚石图像分割结果的影响。
1 图像分割模型架构和数据集构建
基于空洞卷积神经网络进行金刚石图像分割研究,主要过程为:准备标注出金刚石颗粒的训练样本集、验证集和测试样本数据集;将训练数据输入具有不同结构超参数的网络,对网络进行训练;训练完毕后,对测试样本进行检测。
1.1 网络架构
所用的空洞卷积网络架构与文献[10]提出的网络架构相类似。与全卷积方法相比,空洞卷积架构代替了采样操作,具有保持空间分辨率、扩大感受野的优点,因此在语义分割应用中得到了广泛关注。
所用模型的网络架构如图1。所建网络共包含16层:第1层为输入层,接下来是4组具有不同膨胀系数的空洞卷积层、批量归一化处理层和激活层的组合,之后是具有2个1×1卷积的卷积层,其后是1个softmax 分类层和1个具有逆类权重的输出层。空洞卷积层的过滤器大小为3×3。

图1 空洞卷积神经网络架构
1.2 数据集构建
试验图像采集时所用的金刚石粒度号为50/60。金刚石均匀分布在多种颜色的背景上,采用VISION1000数字显微镜在斜光源照明条件下对金刚石进行图像采集。每幅图像的大小为2 048×1 536像素。把采集的图像裁剪成132×118像素的小图,每幅图中只包含一颗金刚石,并标注出真值图。本研究中标注的图像是二值图像,即图像像素划分成2类:金刚石(用1表示)和背景(用0表示)。从获得的700幅金刚石颗粒图像中随机挑选图像作为训练集图像、验证集图像和测试集图像,它们之间的数量比例为5∶1∶1。在对模型的训练过程中将训练集图像送入网络模型进行初始化参数训练;利用验证集图像防止模型参数过拟合;最后使用测试图像对模型的训练结果进行评价。网络架构和图像标注都在Matlab平台上进行。
2 空洞卷积网络训练
2.1 图像预处理
所采集的金刚石图像含有很多噪点,对网络训练可能产生不利影响。为此,对输入图像进行了增强处理——去噪和灰度调整。采用了维纳滤波去噪,滤波器窗口大小为[3, 3]。灰度调整采用Matlab的Imadjust函数实现,调整参数为默认值。把原灰度图像中灰度值在[0.01, 0.99]区间内的像素的灰度值线性变换到[0, 255]区间,小于1%的灰度值设置为0, 大于99%的设置为255。这样就增大了灰度差异,提高了对比度。
2.2 试验超参数设置
在本研究中,网络模型的训练采用适应性矩估计算法(adaptive moment estimation, ADAM)。初始学习速率设置为0.001,迭代次数(epoch)固定在15次,批处理大小设置为7、10、20、30和40。4层空洞卷积层中,第1层网络的膨胀系数设定为1,保持不变;其他层的系数则进行了改变,以研究膨胀系数对模型分割性能的影响。第1层到第4层的膨胀系数共试验了4种组合,分别是1-2-3-4、1-2-4-6、1-2-4-8、1-3-6-9。空洞卷积层中过滤器的数量分别为16、32、48和64。
2.3 分割性能评价指标
为评价所研究的金刚石颗粒图像分割方法的性能,选用了2个评价指标:精确率(p)和召回率(r)。计算公式如下[11]:
(1)
(2)
其中,Tp表示金刚石像素中被正确划分为金刚石像素类的样本个数;Fp表示背景像素被划分于金刚石像素类的样本个数;Fn则表示金刚石像素中被划分为背景像素类的样本个数。因此,精确率指金刚石像素中被正确归类为金刚石的比率,数值越高,分割性能越好。召回率是指正确归类为金刚石的像素占金刚石总像素的比率,召回率越高,网络的分割性能越好。一般来说,精确率越高,召回率越低;而分割性能通常要综合这2种指标来评价,实现精确率和召回率的平衡。
3 结果与分析
3.1 批处理大小对分割性能的影响
神经网络训练时,可以一次性将整个数据集输入神经网络,让神经网络利用全部样本来计算迭代时的梯度,也可以一次只输入一个样本。折中的办法是每次输入一部分样本(batch)让神经网络完成迭代。更大的批处理规模(batch size)更能准确地计算出梯度,批处理规模越小所得的梯度越近似。直觉上好像更大的批处理规模更好,因为其梯度更“准确”。实践中,由于深度模型的代价函数不平整,完整的梯度常常使模型陷入局部极小值,所以大的批处理规模带来的准确的梯度有可能不利于处理结果,有时候小的批处理规模引起的噪声可以更快地找到更好的极小值。但批处理规模太小可能导致网络训练的稳定性差,对学习速率的设置要求也更高,可能造成恶性振荡而无法收敛。
图2反映的是批处理大小对训练的网络分割金刚石图片精确率和召回率的影响,图3所示为网络训练的精度曲线。由图2可以看出:当批处理规模从7幅增大到40幅时,模型的分割精确率逐步从0.948下降到0.919;但批处理大小对召回率的影响不大,其稳定在0.973~0.984之间。可见,从分割精度考虑,批处理规模取较小的值比较合理。由于批处理规模为7幅时,网络训练时已出现明显的振荡(图3),继续缩小批处理规模不太合适。因此后续研究中,批处理规模都设定为7幅。
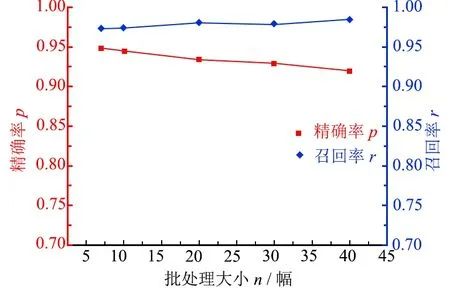
图2 批处理大小对模型性能的影响
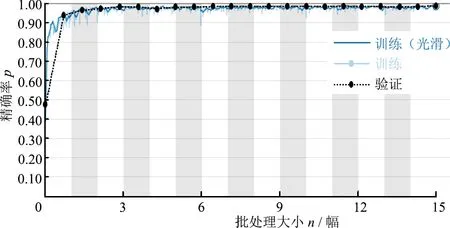
图3 网络训练的精度曲线
3.2 过滤器数量对分割性能的影响
卷积层中过滤器的数量决定卷积层的输出深度,影响图像高层特征的抽取。图4是过滤器数量对模型分割性能的影响曲线。当过滤器数量从16增加到48时,模型的分割精度从0.923升高到了0.967;继续增加过滤器数量到64时,分割精度却大幅下降至0.894。过滤器数量对召回率的影响则与之相反。当过滤器数量为16时,召回率是0.980;过滤器数量为48时,召回率是0.959。但过滤器数量进一步增加到64时,召回率又回升到了0.987。因此,从平衡模型的分割精度和召回率考虑,对于本研究涉及的金刚石图像,神经网络过滤器数量选择为48比较合适。
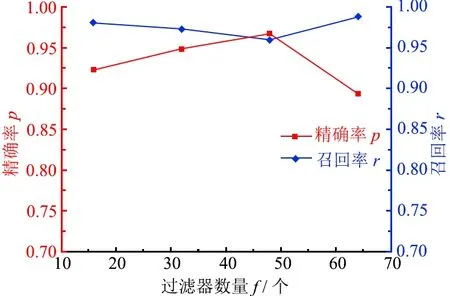
图4 过滤器数量对模型性能的影响
3.3 空洞卷积膨胀系数对分割性能的影响
在图像分割领域,为了增大感受野,传统的网络(比如全卷积网络)采用先池化再上取样的办法。在尺寸先减小再增大的过程中,会造成一些信息的损失而影响精度。空洞卷积网络与传统方法相比,好处是不做池化的情况下,通过膨胀系数加大了感受野,让每个卷积输出都包含较大范围的信息。为了保证卷积核的连续性,尽量让所有的像素都参加计算,需要采用不同的膨胀系数组合来提高计算的覆盖率。因此,在多层网络中,各层的膨胀系数组合对于网络性能有着重要影响。
不同膨胀系数组合对模型精确率和召回率的影响如图5。图5中横坐标轴的数字组合代表各个网络不同空洞卷积层膨胀系数的组合。比如1-2-3-4,表示第1层空洞卷积层的膨胀系数为1,第2层的为2,第3层的为3,第4层的为4。
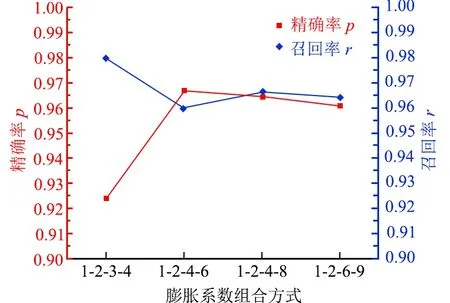
图5 不同膨胀系数组合对模型分割性能的影响
由图5可以看出:当膨胀系数较小时(1-2-3-4),网络分割的精确率较低,召回率较高;其余的3种膨胀系数组合造成的分割精确率和召回率差异不大。含1-2-4-8膨胀系数组合的网络的分割精确率和召回率分别为0.965和0.966,稍有优势。因此,确定网络的最优膨胀系数组合为1-2-4-8。
3.4 优化后网络与传统方法分割性能对比
图6和表1对比了超参数调优后的神经网络与传统的全局阈值(最大类间方差法)、自适应阈值法对金刚石图像的分类能力。

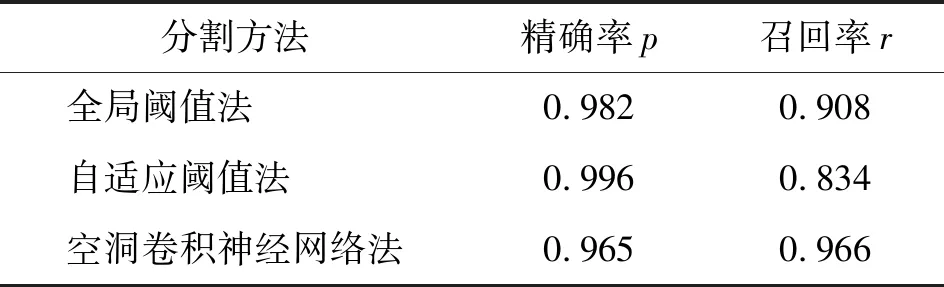
表1 金刚石图像分割实验结果
由表1可以看出:采用传统方法尽管可以得到很高的精确率,但是召回率比较低。也就是说,很多应划分为金刚石的像素被归类成了背景像素。由于金刚石晶面对光的反射和透射,所获取的金刚石图像难免存在大小不等的亮斑(图6a,尤其是箭头所指区域)。这些亮斑在灰度值上与背景的灰度值更为接近。因此,基于阈值的分割方法无法把亮斑区域归类到金刚石(图6b、图6c),所提取的金刚石图像内部含有孔洞或边缘残缺。而基于空洞卷积的神经网络法对这些亮斑有良好的归类能力(图6d),召回率有明显提高,所提取金刚石颗粒的完整性得到很大改善。也就是说,能够把金刚石内部的亮斑或发光的金刚石晶面“智能”地归类为金刚石,而不是归类为与之灰度值更为接近的背景,从而使分割的金刚石颗粒图像更为完整。
4 结论
针对金刚石颗粒图像分割要求,提出了基于空洞卷积神经网络的语义分割模型。构建了含有16层的深度学习网络和小型的金刚石颗粒图像分割数据集,在其上的网络训练和测试结果表明:
(1)空洞卷积网络的批处理大小、过滤器数量和卷积层膨胀系数对模型的分割性能都有明显影响;
(2)经超参数优化后的神经网络能够对金刚石颗粒图像进行良好分割,对测试图片可以达到0.965的精确率和0.966的召回率,较传统的阈值分割法有较大优势。
该方法很好地解决了金刚石颗粒中亮斑的归类问题。

