粘弹塑性土工格栅加筋尾矿流变模型研究
易富,杜常博,李军,张利阳,张晋
(1.辽宁工程技术大学 a.建筑与交通学院;b.土木工程学院, 辽宁 阜新 123000;2.沈阳建筑大学 土木工程学院, 沈阳 110000;3.西南交通大学 土木工程学院 成都 610031)

最初常用弹塑性理论研究土工合成材料的本构关系,不考虑土工合成材料变形的时间效应,如线性、双曲线、多项式[2-5]等经验模型;而近年来,考虑到土工合成材料的流变性能,一些学者提出了经验模型、元件模型和内时模型等流变模型[6-9],表征加筋材料的粘弹塑性变形特征,并把筋材和土体看成宏观均匀的复合材料,认为筋土的相互作用表现为内力[10-11];在此基础上,研究土工格栅加筋土的本构模型也考虑了加筋材料的流变特性,如Sawicki等[12]、肖成志等[13]、李丽华等[14]、周志刚等[15]均采用土工格栅三参数粘弹性模型,提出了考虑筋材蠕变性能的加筋土流变模型,但现有的三参数粘弹性模型没有考虑土工格栅的塑性特征,无法全面准确地反映加筋结构中土工格栅长期荷载作用下的力学特性。
在考虑土工格栅长期荷载作用下塑性特征的基础上,建立了适用于加筋尾矿的流变模型,假设土工格栅是粘弹塑性体,尾矿是弹塑性体,把加筋尾矿复合体看成一个整体,整个复合体受力分为尾矿处于弹性或塑性状态两个阶段,分别建立两个阶段的模型方程,推导出了这两个阶段加筋尾矿复合体的本构关系表达式。
1 加筋尾矿复合体流变模型推导
1.1 基本假定
假定加筋尾矿复合体是宏观均匀各项异性的复合材料,其中,土工格栅为粘弹塑性材料,尾矿是弹塑性材料,满足Mohr-Coulomb强度准则;假设土工格栅与尾矿之间完全粘结,没有相对滑动,格栅只是处于受拉状态,加筋复合体的剪应力、剪应变均由尾矿承担;把加筋尾矿复合体变形分成两个阶段进行分析,第1阶段尾矿表现为弹性,尾矿开始进入塑性状态为第2阶段;整个阶段加筋尾矿复合体均为粘弹塑性。
1.2 土工格栅粘弹塑性模型
目前,许多学者在研究土工格栅元件模型时大多采用三参数粘弹性模型,该模型由弹簧和Kelvin体两部分串联而成,能够反映土工格栅低应力下的蠕变规律。但是,大量土工合成材料的蠕变试验结果显示,三参数粘弹性模不能准确计算出土工格栅的起始蠕变点,也无法反映塑性变形规律,所以,此模型无法很好的应用于理论计算。文献[12]提出在三参数粘弹性模型的基础上增加一个线性塑性滑块,改进成四参数粘弹塑性模型(如图1a所示),定义这个塑性元件的单位宽度拉力与塑性应变呈线性关系,且塑性变形不可恢复,这样就能调整土工格栅蠕变的起始应变准确模拟蠕变情况,并能准确预测格栅的应力松弛变化规律。
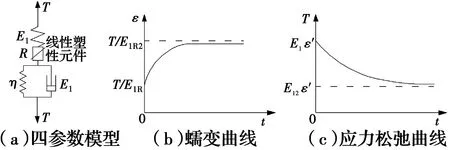
图1 土工格栅四参数粘弹塑性模型及其蠕变、应力松弛曲线Fig.1 Four-parameter viscoelasto plastic model of geogrids and its creep and stress relaxation
经过受力与变形分析,在加载过程中,土工格栅的微分本构关系为
(1a)
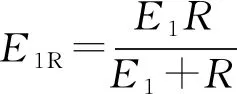
(1b)
式中:E1为弹性元件的刚度系数,kN/m;R为线性塑性元件的塑性模量,kN/m;E2为Kelvin体弹簧的刚度系数,kN/m;η为Kelvin体粘壶的粘滞系数,kN·h/m;T为筋材单位宽度上的拉力,kN/m;ε为对应应变,%;t为蠕变时间,h。
1.2.1 蠕变 令式(1)中荷载T为常数,可得到土工格栅的蠕变方程(见图1(b))为
(2)
在t=0时,土工格栅的初始蠕变为
(3)
在t→∞时,格栅的蠕变达到稳定状态,此时
(4a)
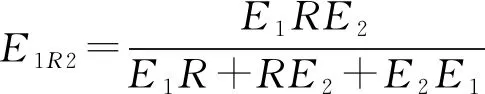
(4b)
1.2.2 应力松弛 在t=0时,尚未发生流变变形,筋材保持弹塑性应变不变,即
ε(t=0)=ε1+ε2=常数
(5)
随着应力松弛的开始,流变逐渐产生,因塑性应变不可恢复,那么弹性应变减少,粘性应变增加,二者之和依然为常数。
ε′(t>0)=ε1+ε3=ε-ε2=常数
(6)
式中:ε′为部分应变的组合,%。
(7a)
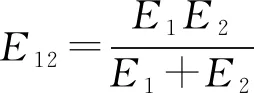
(7b)
在t=0时,对土工格栅应力松弛方程进行了瞬时响应计算,从公式(7)中可表示为
T(t=0)=E1ε′
(8)
由方程(7)可得出土工格栅在恒定应变下渐进行为(即t→∞)的应力松弛情况为
T(t→∞)=E12ε′
(9)
1.3 加筋尾矿复合体模型的建立

ns+nr=1
(10)
(11)
式中:nr=e/Δh,其中,e为格栅厚度,m;Δh为格栅层间距,m。
本文研究平面应变状态下的加筋尾矿结构,假定筋材只在x方向上工作,图2所示为加筋复合体在平面应变状态下宏观应力与微观应力关系示意图,假定格栅只处于受拉状态,不考虑格栅在厚度方向的压缩和弯曲变形,则式(11)可简化为
(12)
(13)
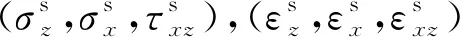
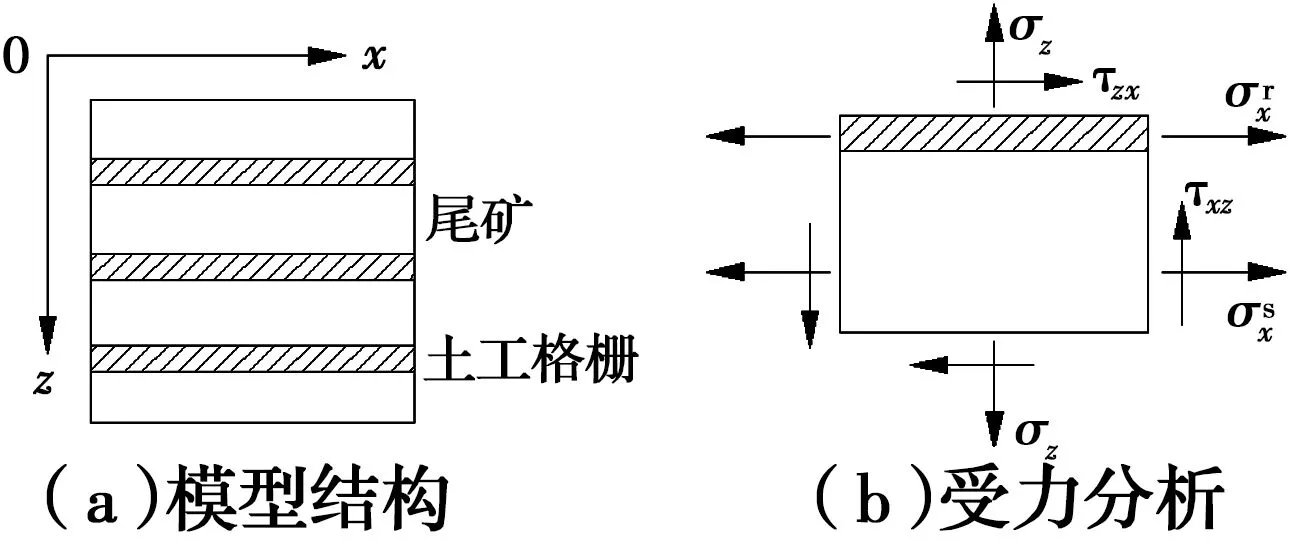
图2 加筋尾矿宏微观应力的关系示意图Fig.2 Sketch of relationship between macro- and micro stress of reinforced
1.3.1 第1阶段:尾矿处于弹性状态 当尾矿处于弹性状态而土工格栅为粘弹塑性材料时,由平面应变条件下广义Hooke定律得
(14)
(15)
式中:Es为尾矿变形模量,MPa;vs为泊松比。
将式(10)~式(13)代入式(14),整理得
(16)

(17)
结合式(16)和式(17),并考虑筋材在加筋复合体中所占的体积比很小(ns≅1),可得
(18)
将式(18)代入式(1),得
(19a)
式中:
(19b)
假定土工格栅的初始应力为T0,求解方程式(19)可得
(20a)
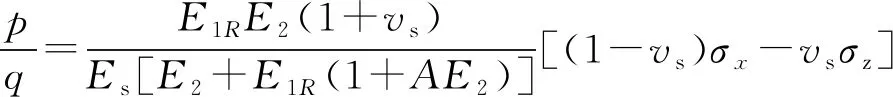
(20b)。
式中:tp为塑性到达时间(加筋复合体达到第2阶段所需要的时间),h。
根据式(10)和式(17)可得尾矿水平应力为
(21)
为求得加筋尾矿复合体的塑性到达时间tp,假定尾矿为弹塑性材料,满足Mohr-Coulomb准则,所以有[14]
(22)
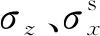
(23)
(24)
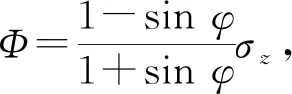
(25)
1.3.2 第2阶段:尾矿进入塑性状态 当尾矿进入塑性状态时,尾矿符合屈服条件式(23)。根据与破坏条件相关联的流动法则,塑性应变的表达式为[14]
(26)
式中:λ为塑性阶段的变形。
此时,尾矿处于塑性状态,应满足条件
(27)
将式(23)代入上述流动法则得
(28)
假定加筋复合体的宏观应力不变,即dσz=dσx=dτ=0,由式(21)得
(29)
再将式(29)代入到式(28),得
(30)
因此,当尾矿进入塑性状态后,加筋复合体的应力保持不变,尾矿的塑性流动由加筋复合体粘弹塑性变形决定,此时土工格栅加筋尾矿的流变模型为
(31)
求解式(31)微分方程,得到尾矿塑性状态时加筋复合体的水平变形方程为
(32)
式中:εp为加筋复合体在弹性结束时、塑性开始时的应变,%。
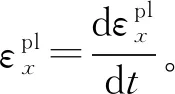
(33)
通过上述推导可得尾矿处于弹性和塑性状态两个阶段的加筋尾矿复合体的本构关系:第1阶段尾矿处于弹性状态时,式(20)描述了筋材应力的降低,导致在尾矿中的微观应力重新组合,直到尾矿达到屈服条件,方程式(18)给出了此阶段加筋复合体的应变关系式,式(17)和式(21)分别给出了加筋复合体中筋材和尾矿的应力关系式;第2阶段尾矿达到屈服条件进入塑性状态时,塑性到达时间可由式(25)确定,此阶段加筋复合体的应力恒定,整个加筋尾矿复合体应变由于筋材的蠕变而增大,第2阶段的变形函数可由式(33)给出,再结合式(26)和式(32)可得出第2阶段的水平和竖向变形方程。
以上分析可知,加筋复合体的受力不仅与土工格栅和尾矿的应力有关,还与土工格栅材料特性、尾矿物理特性、加筋层间距及时间有关。
2 模型参数求解
2.1 土工格栅模型参数求解
采用栾茂田[6]的试验,他对不同规格的单向土工格栅进行了蠕变试验,选取型号EG65R的土工格栅的试验数据。EG65R土工格栅的极限荷载为65 kN/m,蠕变数据选取荷载作用为31.2、33.4、35.5 kN/m,而应力松弛选取应变为4%、5%、6%,具体数据如图3所示。

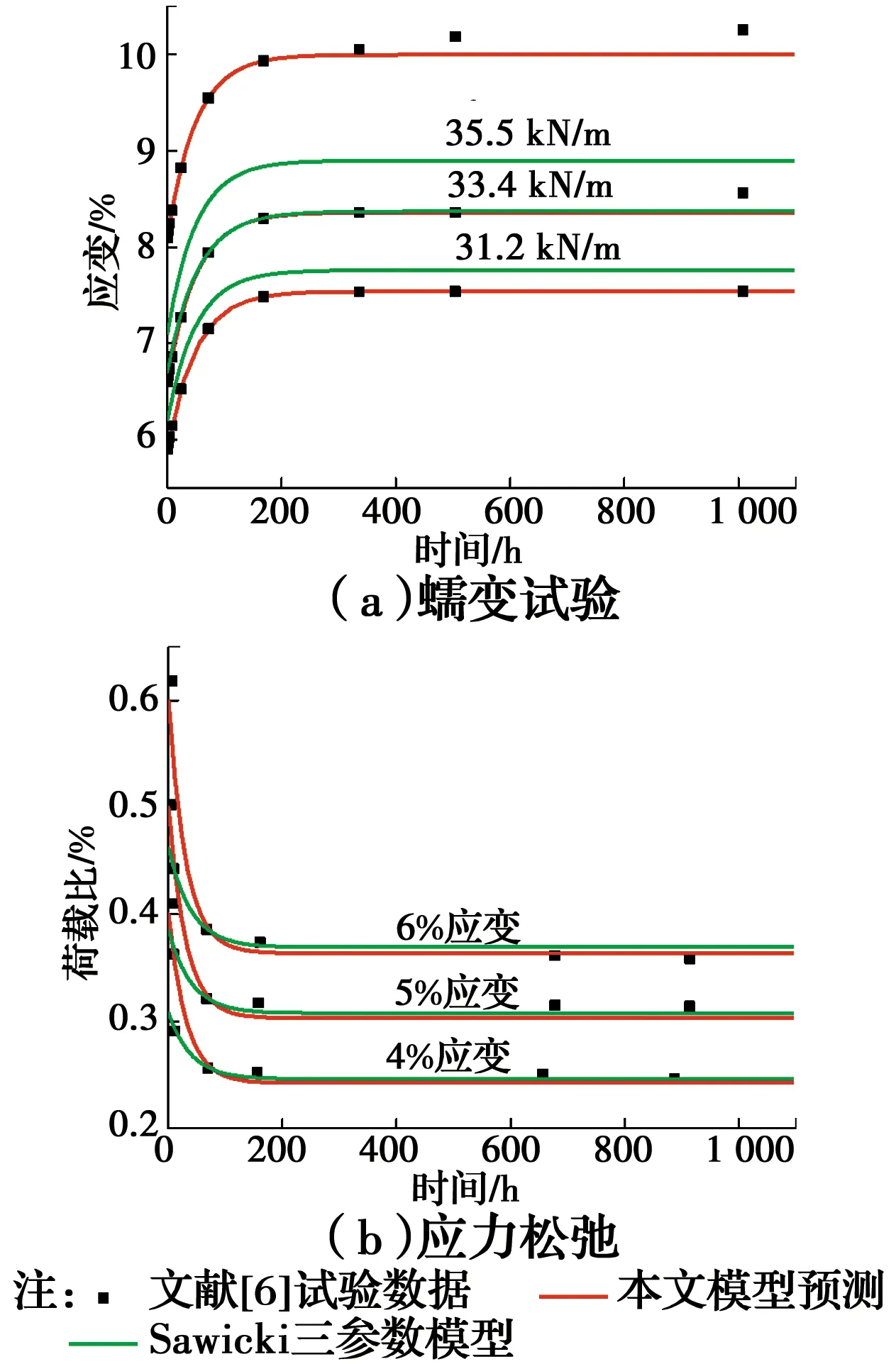
图3 试验数据与本文模型对比Fig.3 Comparison between experimental data and the model of this

表1 土工格栅粘弹塑性模型的四参数值Table 1 Four parameter values of viscoelasto plastic model of geogrids
2.2 加筋复合体模型参数求解
假定有一座采用本文土工格栅加筋的尾矿坝,坝体中土工格栅处于3.25 kN/m的应力状态下(即应力水平为5%)[15],取尾矿堆积坝深度z方向3 m的某加筋尾矿单元为研究对象,尾矿具有的物理性质指标见表2。

表2 尾矿物理参数取值Table 2 The physical parameter value of tailings
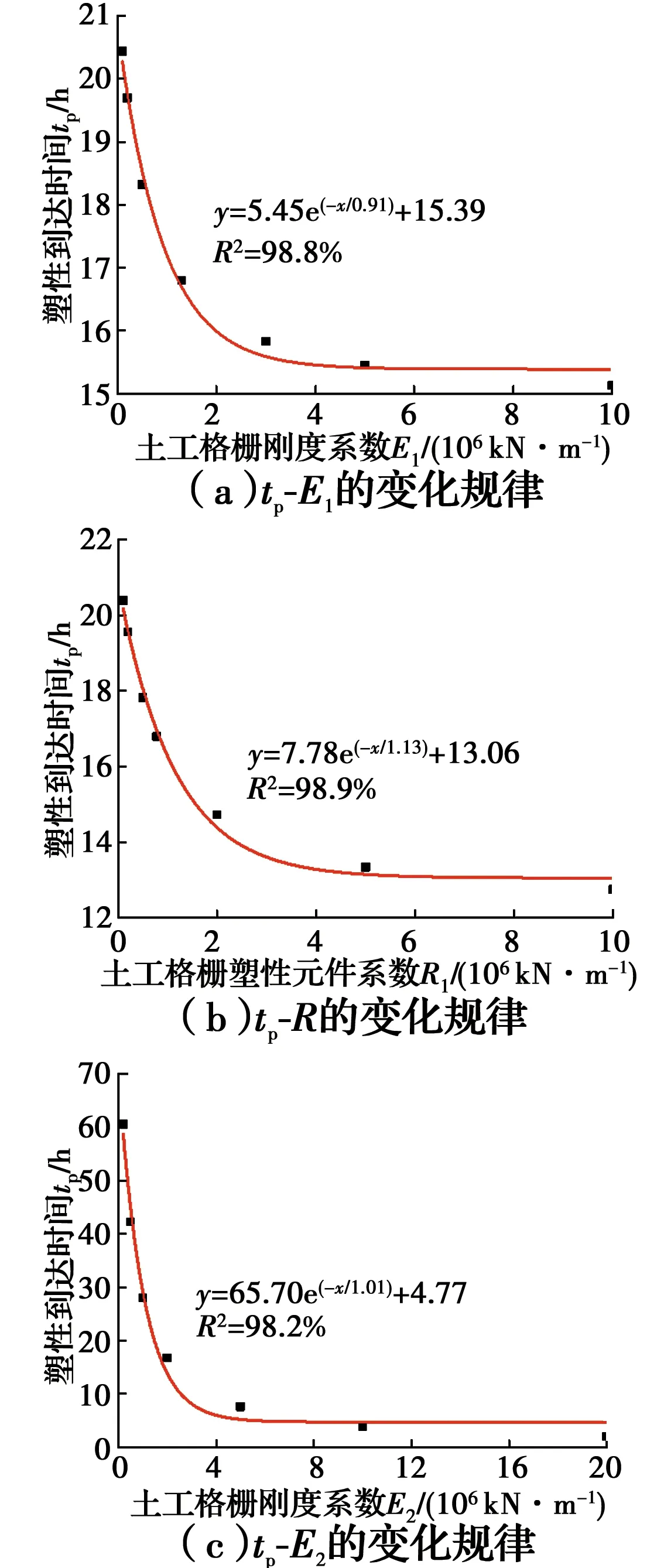
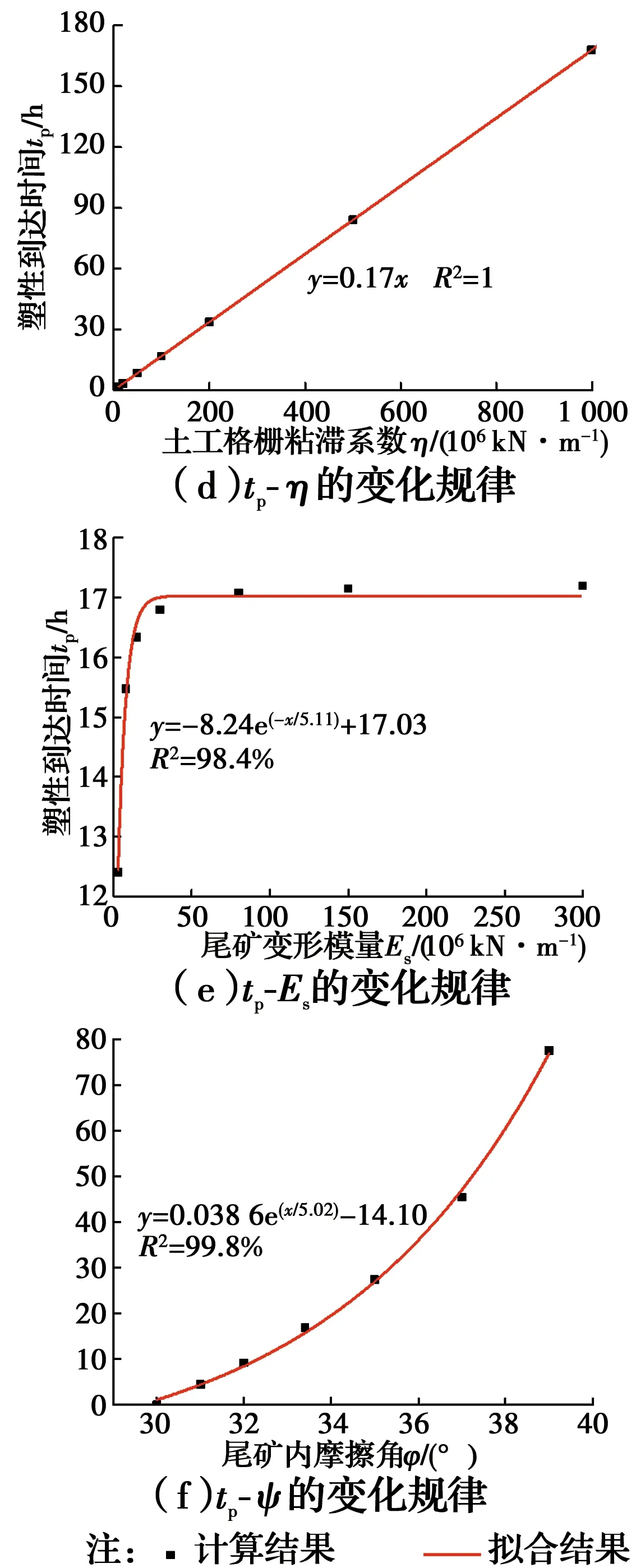
EG65R土工格栅处于5%应力水平时,塑性元件的模量为R=0.78×103kN/m,再将表1中土工格栅的弹簧的刚度系数E1、E2、粘滞系数η及格栅层间距Δh和尾矿参数代入式(25),得到加筋尾矿复合体的塑性到达时间tp=16.8 h。第1阶段加筋尾矿复合体的宏观与微观状态如图4所示。
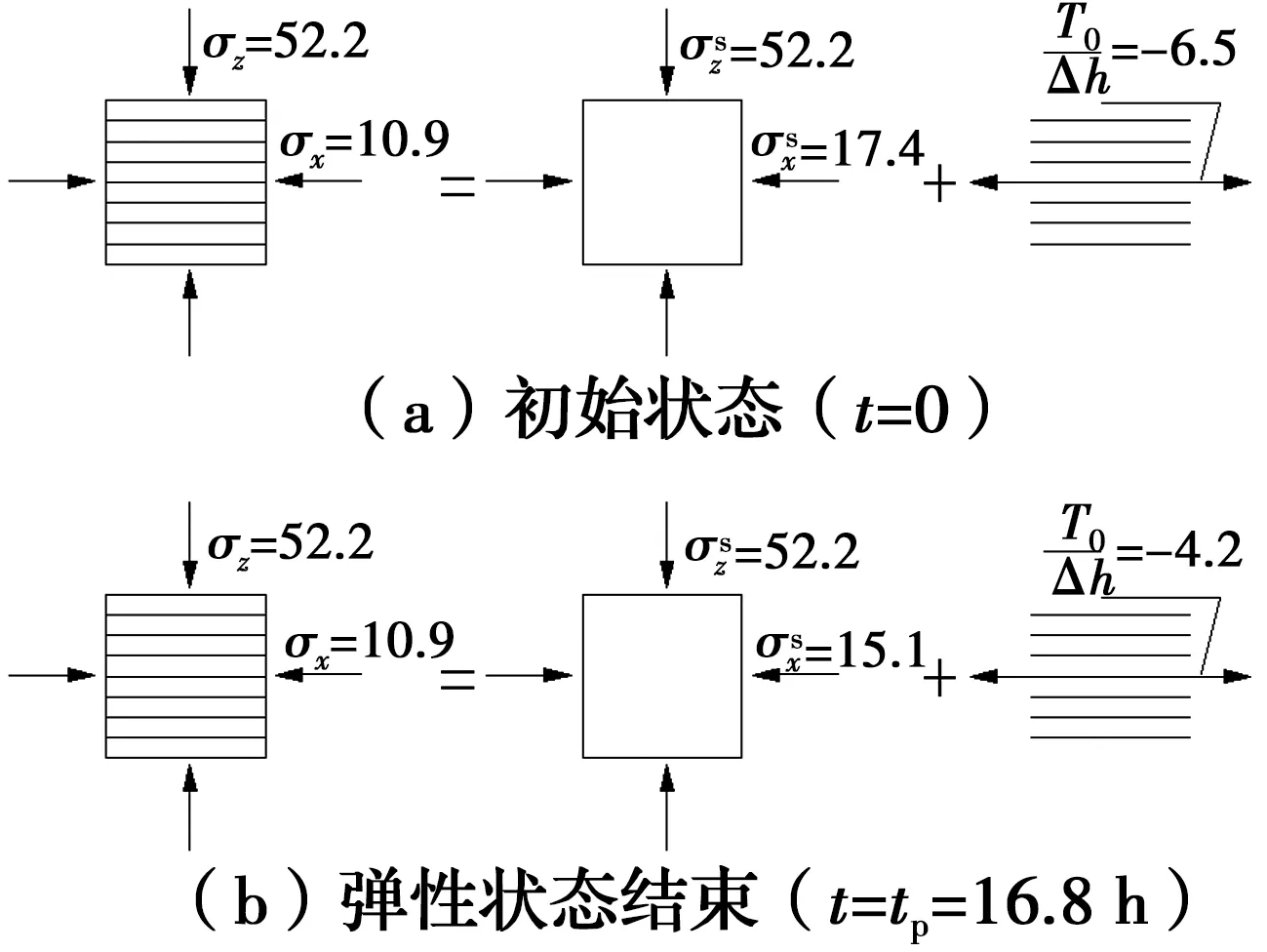
图4 加筋尾矿复合体第1阶段宏微观状态(单位:kPa)Fig.4 Macro-and micro stress state of reinforced tailings complex in the first
2.2.1 第1阶段 由式(20)得出尾矿中格栅处于3.25 kN/m应力状态下的应力松弛表达式为
T=(-3.176 8e-0.026 3t-0.073 2)×103
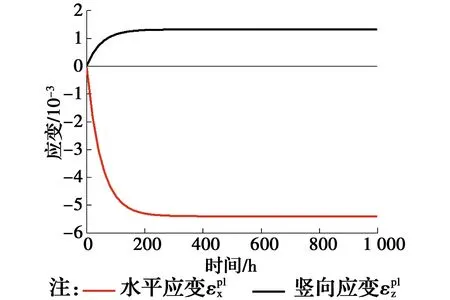
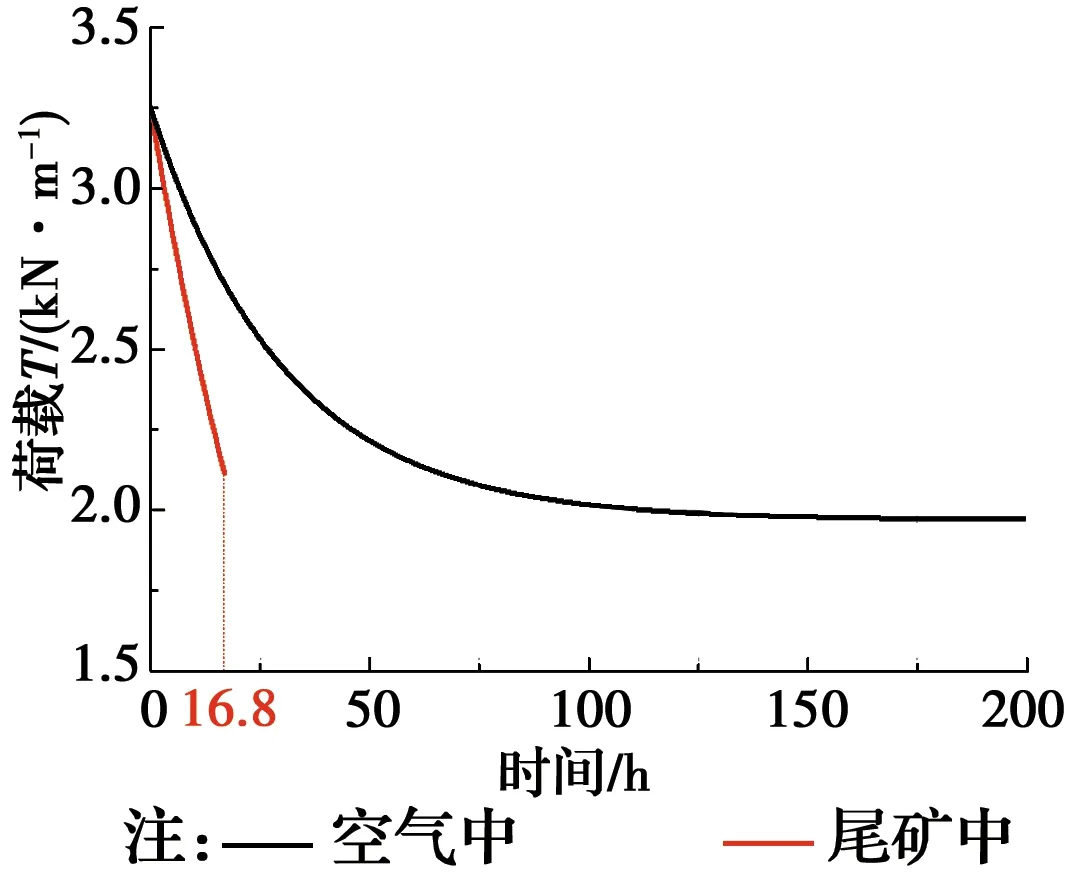
(0 (34) 将式(34)代入式(18)得到加筋复合体的弹性应变为 εx=0.198 6×10-3×(e-0.026 3t-1) (0 (35) 此时,当尾矿处于弹性状态下,土工格栅和尾矿的应力分别为 (36) (37) 如图5所示,根据式(36)和式(37)计算可得到加筋复合体中尾矿达到塑性状态前格栅和尾矿单元的应力随时间变化情况。由图5可知,当尾矿处于弹性状态时,由于应力松弛,土工格栅和尾矿的应力都随时间逐渐减小,当接近临界时间tp,二者的应力开始趋于平缓。 图5 第1阶段筋材和尾矿的微观应力变化Fig.5 Variation of micro stress of geogrids and tailings in the first 2.2.2 第2阶段 将tp=16.8 h代入式(35),得到加筋复合体第1阶段结束第2阶段开始时的应变εp。 εp=0.198 6×10-3×(e-0.026 3t-1)= -0.070 9×10-3 (38) 再将εp和得到的格栅模型参数代入式(33),得到尾矿在塑性状态时加筋复合体水平变形方程为 εx=5.325 5×10-3e-0.02t-5.396 4×10-3 (t>16.8 h) (39) 综上所述,可知土工格栅处于5%应力水平时,塑性到达时间很小,即加筋尾矿复合体受力很快进入第2阶段,且第1阶段变形比较小,可以忽略不计,整个加筋阶段复合体的应变主要由第2阶段导致,故在进行变形计算时,以第2阶段的变形为主。 由式(26)、式(32)和式(33)结合式(39)可得第2阶段的塑性变形方程式为 (40) 图6所示为第2阶段的塑性应变发展情况,时间t是加筋复合体在第2阶段开始时开始计量的,第2阶段塑性应变在开始时迅速增加,在t=300 h后趋于稳定。 图6 由筋材蠕变引起的塑性应变变化Fig.6 Variation of plastic strains due to creep of 2.2.3 空气和尾矿中格栅应力松弛的对比情况 由式(7)可得格栅处于3.25 kN/m应力状态下的应力松弛表达式为(此时格栅保持应变0.25%不变) T=(1.280 3e-0.033t+1.969 7)×103 (41) 由式(34)可得尾矿中格栅处于3.25 kN/m应力状态下的应力松弛表达式为 T=(3.176 8e-0.026 3t+0.073 2)×103 (0 (42) 图7所示为置于空气和尾矿中土工格栅应力松弛的对比情况。置于空气中土工格栅应力松弛在时间为200 h左右时,应力将稳定在1.9 kN/m状态下;而置于尾矿中的格栅应力松弛在塑性到达时间时处于2.2 kN/m状态下,之后,尾矿进入塑性状态,格栅应力松弛完成,应力将保持不变;同时,对比空气和尾矿中的格栅应力松弛可知,室内条件下的应力松弛比实际条件下的要大,但实际条件下的应力松弛要比室内条件下的快。当格栅置于尾矿中,由于格栅与尾矿的相互作用,土工格栅应力松弛将快速完成,进而随着尾矿进入塑性状态,加筋复合体的应力保持不变。 图7 空气和尾矿中格栅应力松弛的对比Fig.7 Comparison of stress relaxation of geogrid in air and 为了探讨土工格栅粘弹塑性模型参数和尾矿强度参数对加筋复合体塑性到达时间tp的影响规律,结合以上分析给定各参数基准值见表3。 表3 各参数的基准值Table 3 Baseline values of each parameter 如图8所示,根据式(25)计算得到加筋尾矿复合体塑性到达时间tp随土工格栅粘弹塑性模型参数E1、E2、R、η和尾矿变形模量Es及内摩擦角φ的变化规律。由图8可知:tp与E1和tp与R都呈负指数关系减小,变化不大,在10~20 h之间变化,最后都趋于稳定;tp与E2也呈负指数关系减小,变化相对较大,在0~60 h之间变化;tp与粘滞系数η呈线性正相关,变化较大;tp与Es呈负指数关系增大,变化幅度不大,当量Es超过30 MPa,tp达到稳定状态;tp与φ呈指数关系增大,增大幅度较大。 进一步分析可知,加筋尾矿复合体塑性到达时间tp受土工格栅粘弹塑性模型中Kelvin系数E2、η和尾矿内摩擦角φ的影响显著,受格栅模型内弹性元件系数E1和塑性元件系数R及尾矿变形模量Es影响不明显。 图8 塑性到达时间tp随不同参数的关系Fig.8 The relationship between the plastic arrival time 1)土工格栅四参数粘弹塑性模型能够准确反映土工格栅在低应力水平下的两阶段衰减型蠕变和应力松弛变化规律。 2)提出了粘弹塑性土工格栅加筋弹塑性尾矿的简化模型,将加筋复合体受力分析分为两个阶段,分别对应尾矿处于弹性状态和塑性状态,第1阶段,对于承受恒定应力的加筋尾矿复合体,筋材中的应力随时间减小,导致尾矿中的微观应力重新组合,直到尾矿达到屈服条件进入第2阶段,筋材的应力开始保持不变,整个加筋复合体的应变会随着筋材的蠕变而增加。 3)加筋尾矿结构中格栅处在低应水平力时,加筋尾矿复合体受力会很快进入第2阶段,且第1阶段变形较小,整个加筋阶段复合体的应变主要由第2性阶段导致。 4)加筋尾矿复合体的塑性到达时间tp,受土工格栅粘弹塑性模型中Kelvin元件系数E2、η和尾矿内摩擦角φ的影响显著,受模型内其他参数E1、R和尾矿变形模量Es影响较小。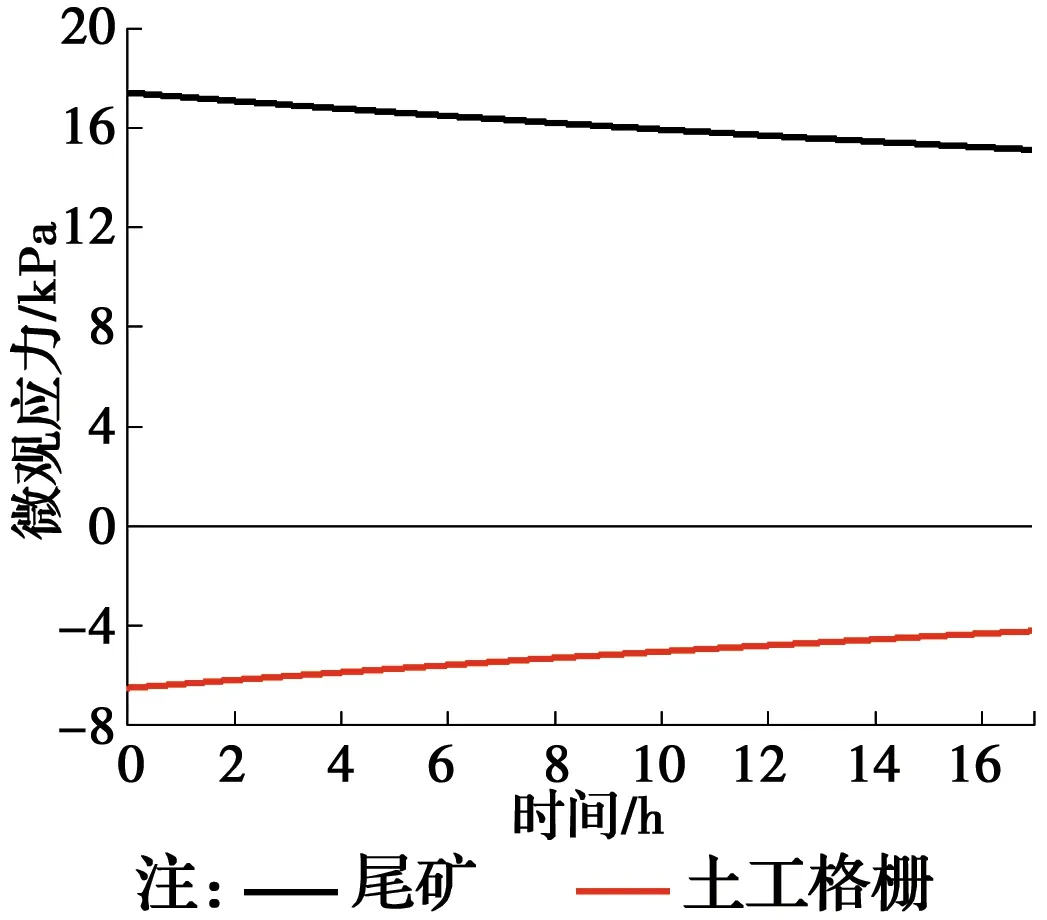
2.3 流变模型参数对塑性到达时间tp的影响分析
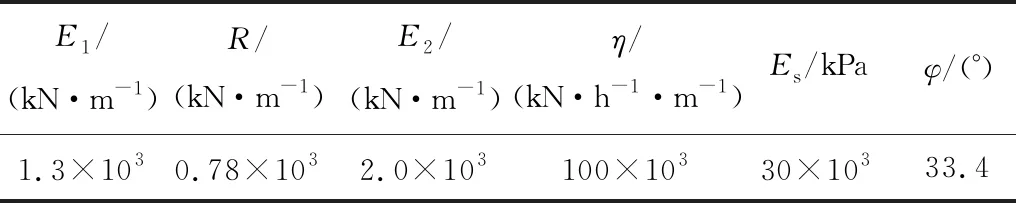
3 结论

