永磁同步电机伺服系统的自抗扰控制

王 帅,康尔良

(1.哈尔滨理工大学,哈尔滨150080;2.黑龙江省高校直驱传动系统创新中心,哈尔滨150080)

0 引 言

近年来,电动汽车、数控机床、多种武器随动及载人航天对电机控制系统的要求不断提高,另一方面,伴随处理器的性能迅速提高,先进的控制算法不断提出,交流伺服系统扮演着越来越重要的角色[1]。而永磁同步电机(以下简称PMSM)具有功率密度高、损耗低、易加工等特点[2],被越来越多地应用于伺服领域。因此,PMSM构成的伺服系统控制技术成为当今的研究热点。PMSM具有参数时变、强耦合、变非线性的特点[3],传统的PID控制器是“基于误差反馈来消除误差”的控制方法,能在一定程度上抑制常值扰动或者慢变扰动。然而若要整个系统达到对负载的突加扰动进行迅速、准确、微超调的动态响应,传统的PID控制器就无法满足了。

本文将自抗扰控制引入PMSM伺服系统转速环和电流环中,从控制结构上将转速和电流环中的PID控制器变为自抗扰控制器(以下简称ADRC),可以省去大量调配参数的时间,减小超调及消除稳态误差。在建立PMSM伺服系统数学模型的基础上,结合自抗扰控制技术理论设计出转速环一阶和电流环一阶ADRC,并进行相应的仿真研究与实验验证。

1 PMSM的数学模型

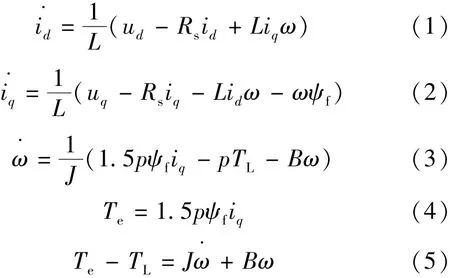
一般来说,通过对电机微分方程的研究来得出PMSM伺服系统的特性。当PMSM转子结构为表贴式时可得Ld=Lq=L,对该电机采取id=0矢量控制策略时,可得PMSM状态方程[4-6]:式中:ud,uq为电机d,q轴电压;L为电机同步电感;id,iq为电机d,q轴电流;ψf为转子磁链值;ω为电机转子电角速度;p为电机极对数;J为转子转动惯量;Rs为电机定子电阻;Te为电磁转矩;B为摩擦系数。

2 基于ADRC的PMSM伺服系统的模型搭建

2.1 ADRC数学模型

ADRC由跟踪微分器(以下简称TD),非线性状态误差反馈律(以下简称NLSEF),扩张状态观测器(以下简称ESO)组成[7-9]。

二阶最速离散TD表达式如下:

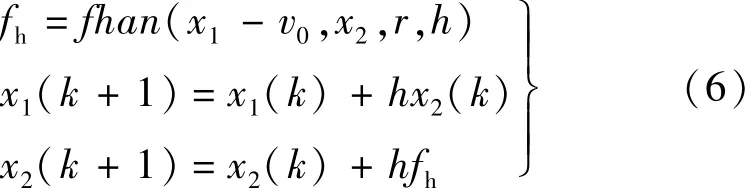
式中:v0为系统输入;x1为系统输入的跟踪值;x2为v的近似微分;fhan(x1,x2,r,h)的具体表达式:

式中:r为速度因子;h为滤波因子[10-11]。

ESO对二阶系统进行观测时的公式算法如下:

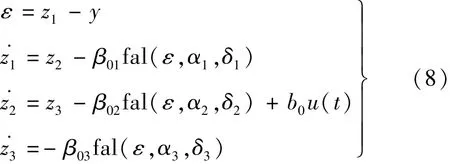
式中:e为误差估值;y为被控对象输出值;z1为被控对象输出估计值;z2为z1的微分信号;z3为系统内外扰动的估计值;α1,α2,α3为非线性因子;β1,β2,β3为输出误差矫正增益;b为系统扰动补偿系数;δ为滤波因子[12-14]。 fal(e,α,δ)的表达式如下:

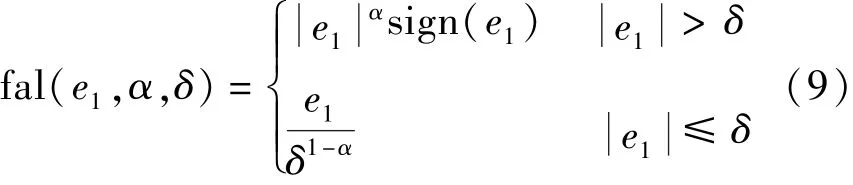
ESO是一个动态过程,它可以将系统的自身扰动与外部扰动相组合,形成一个新的状态变量,并进行实时计算观测。ESO的计算机理是根据输入量与输出量的变化计算,不依赖于系统本身的数学模型,可以大幅度提高系统的鲁棒性。

采用fal函数构成的NLSEF算法公式如下[15]:

式中:αi,βi和δ均是控制器参数,把TD发出的多个参考量与ESO实时监测的变化量做差,并进行非线性组合,能够明显减小系统稳态误差,同时避免了稳态高频颤振。

引入扰动估计补偿后的控制量:

综上,通过ESO对负载变化实施同步监测并补偿,能够达到对系统动态补偿线性化的目的。

2.2 基于ADRC的PMSM伺服系统的设计

传统的位置-转速-电流三闭环矢量控制系统中每一环都是采用PID控制器,本文设计的控制器在保留原系统位置环控制算法不变的情况下,将转速环和电流环中的PID控制器分别用一阶ADRC来代替。这样能够更好地估计出影响电动机转速和转矩的内外扰动并对控制量进行适当的补偿,从而达到响应快、减小超调和消除稳态误差的效果。

根据ADRC设计的分离性原理,可以分别设计TD,ESO和NLSEF,然后组合成一个完整的ADRC。

为此,设计的转速环和电流环的TD方程如下:

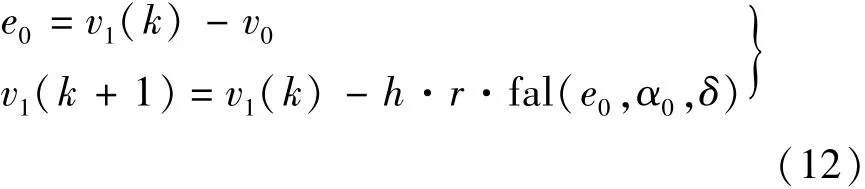
式中:v0为给定的转速或电流;v1(k)为实际运行第k个周期的转速或电流;h为运算周期值;r为跟踪速度决定值。

ESO的方程如下:

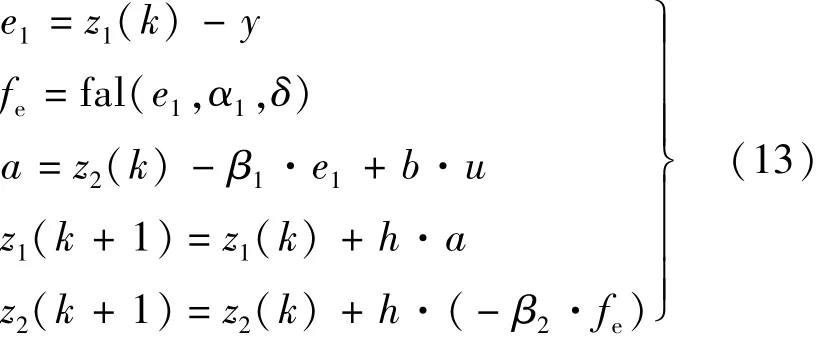
式中:y为检测出的系统转速或电流;z1(k)为系统转速或iq(k)的估计值;z2是对转速环或电流环整个的内外扰动量的观测值;β1,β2是转速或电流观测器的参数。

为了更加准确快速地确定出ESO的参数,引入了带宽的概念。观测器的特征多项式为s2+β1s+β2,为了更好地观测出扰动量和各个状态变量,一般将特征方程设为(s+ω)2,于是把参数β1和β2配置成2ω和ω2的形式。其中,在电流环中整定β1=600,β2=9×104;转速环中β1=800,β2=1.6×105;α1=0.5;δ=0.01。

NLSEF方程如下:

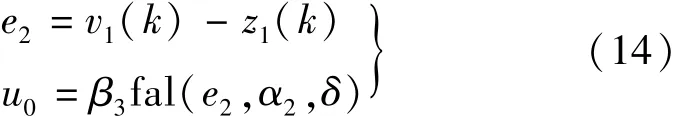
式中:β3是电流环或转速环的控制增益。扰动补偿过程的方程如下:

式中:u是ADRC最终输出的控制量;b是扰动补偿

将以上设计的三个部分相结合,最后通过扰动补偿过程来实现最终控制量的输出,考虑到一阶ADRC可以简化结构省去TD,这样就形成了转速环和电流环一阶ADRC的基本结构,具体框图如图1所示。

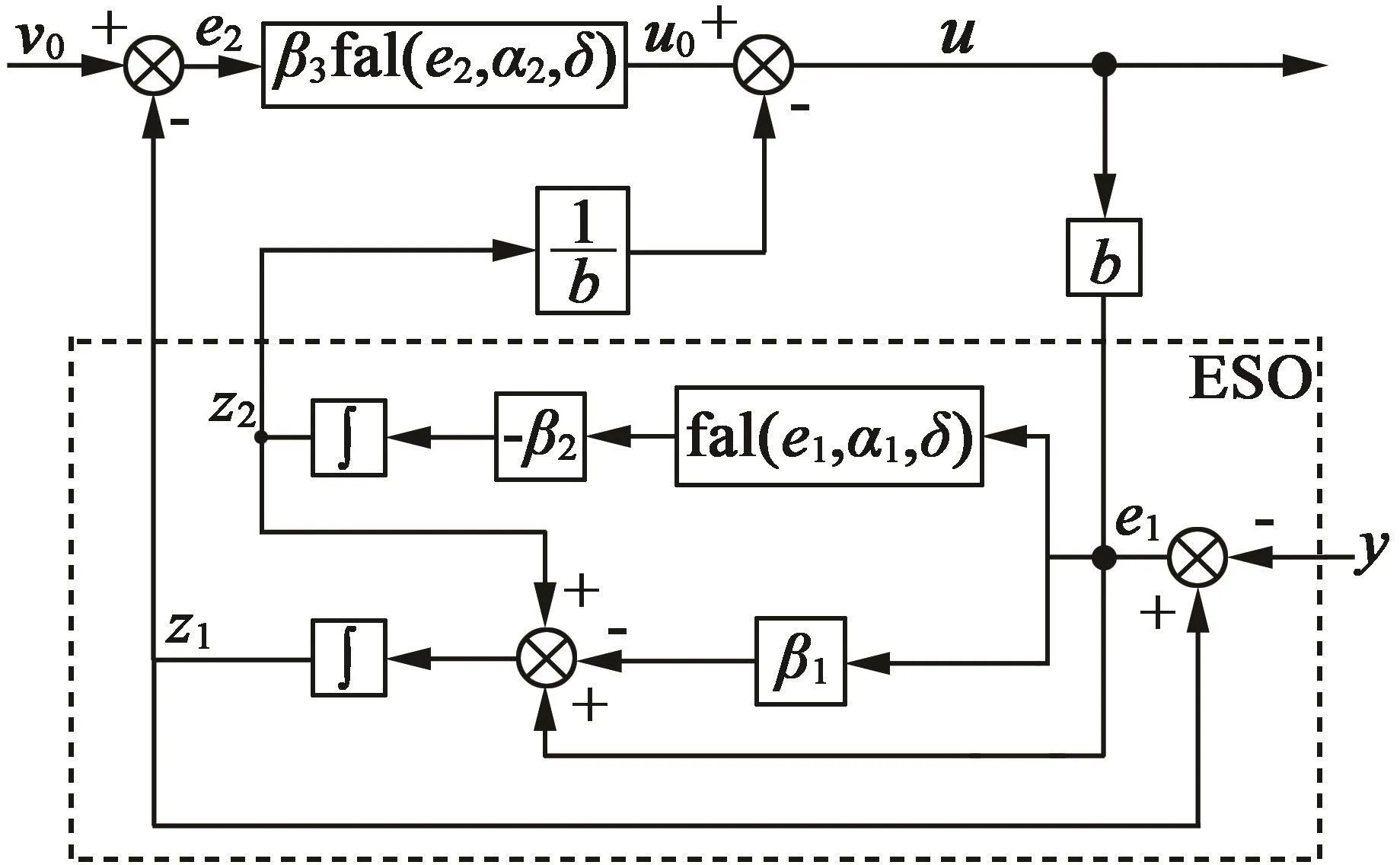
图1 转速、电流环一阶ADRC结构图

3 仿真与实验结果分析

本文对基于ADRC的整个伺服控制系统进行了MATLAB/Simulink数字仿真,PMSM参数如下:定子电阻Rs=2.875 Ω,交直轴电感Ld=Lq=8.5 mH,转动惯量J=0.000 8 kg·cm2,极对数p=4,转子磁通Ψ=0.086 277。鉴于实验条件的限制,实验过程以一台额定功率为750 W、极对数为4、额定转速为3 000 r/min、额定电流为4.2 A、额定转矩为2.4 N·m的PMSM为控制对象。控制用芯片为TI公司的TMS320F28335,搭建PMSM对拖直流电机的实验平台,在定子侧选择串10 Ω/100 W负载电阻和390 Ω/300 W的滑动变阻器作为可变负载使用。使用横河的WT230电参数测量仪及上位机进行波形测量显示。

3.1 仿真结果

目标转速为1 000 r/min,负载转矩为3 N·m时起动系统,t=0.2 s系统趋于稳定时突加8 N·m负载转矩,调整相应参数,把ADRC与传统的PID控制相对比。仿真结果如图2、图3所示。

由图2和图3转速曲线可以看出,在系统带载起动时,传统的PID控制器具有较大的超调量与大幅的振荡;在施加负载转矩后,系统仍伴随较大的振荡,并且在系统趋稳后有一定的稳态误差。而ADRC在系统带载起动时超调量明显减小,振荡明显减弱;在施加负载转矩后系统转速变化平稳,振荡很小且稳态误差几乎为零,对系统转速更加精准的控制。

图2 起动时转速响应曲线

图3 突加负载时转速响应曲线

由图4和图5转矩曲线可以看出,当系统起动时,传统的PID控制器转矩在0.025 s时趋于稳定,而ADRC仅需0.007 s即可达到稳定状态;在系统突加负载转矩后,传统的PID控制器需要0.01 s趋于稳定且伴随较大超调量,而ADRC可瞬间达到稳定且超调量可以忽略。

图4 起动时转矩响应曲线

图5 突加负载时转矩响应曲线

由图6和图7可以看出,传统的PID控制器在突加负载时电流有明显波动,而ADRC在突加负载时电流波动很小,能够在短时内响应给定值。

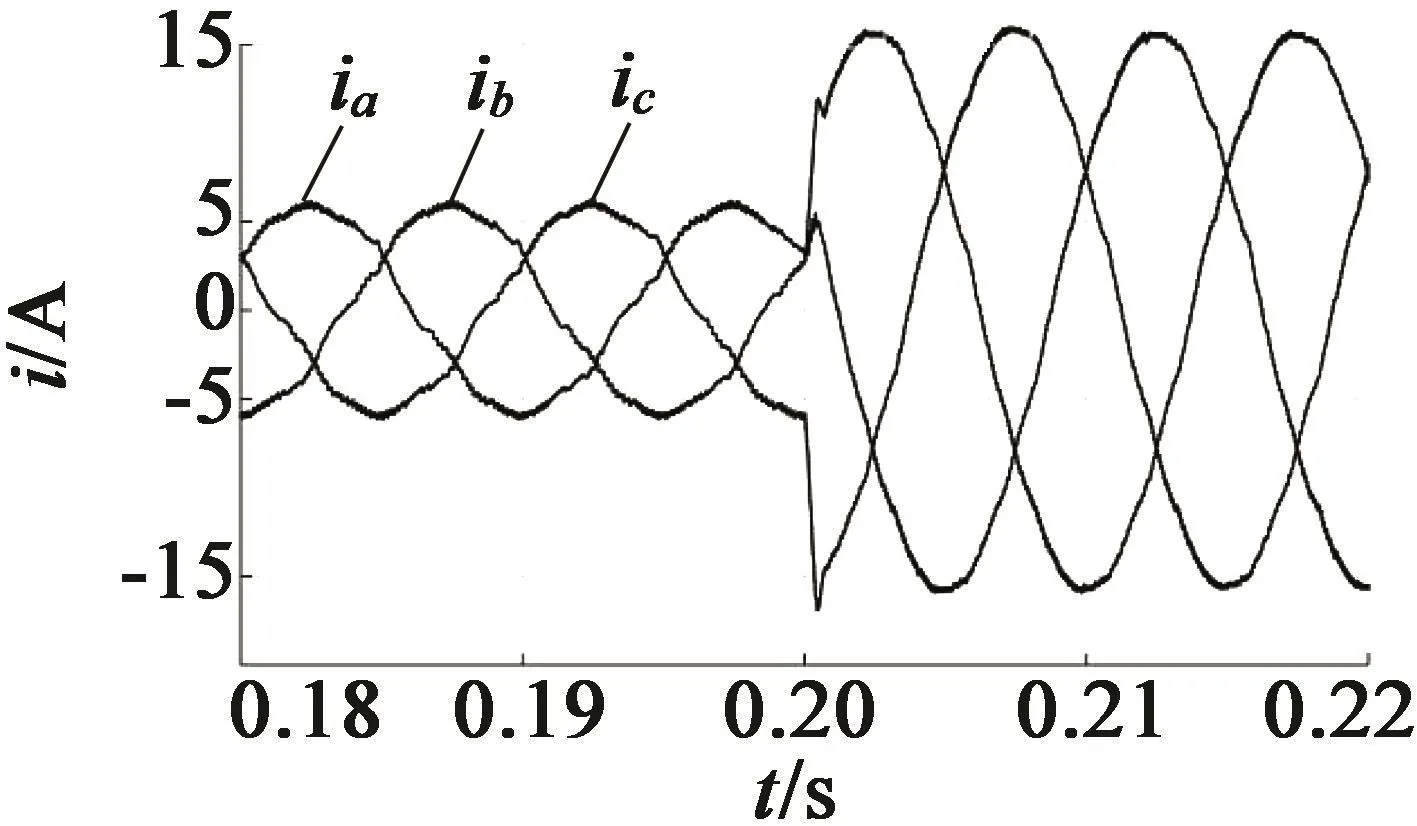
图6 ADRC突加负载电流响应曲线

图7 PID突加负载电流响应曲线

3.2 实验结果

鉴于实验条件的限制,对电机进行了空载和负载实验,并用横河WT230电参数测量仪对电流波形进行采集显示。实验过程中将直流母线电压调整到100 V,转速用按键调节到600 r/min,空载电流波形如图8所示,抖动约为0.3 A;随后将负载串入直流电机定子侧,直流母线电压和转速均不改变,电流波形如图9所示,抖动约为0.8 A。

从实验波形看出,稳定运行时,电流波形稳定。空载和负载时,用按键控制电机加速平稳,突加负载情况下,电流依然可以很快保持稳定。同时,进行了长时间运行,硬件平台没有故障,电机没有出现死机等情况。

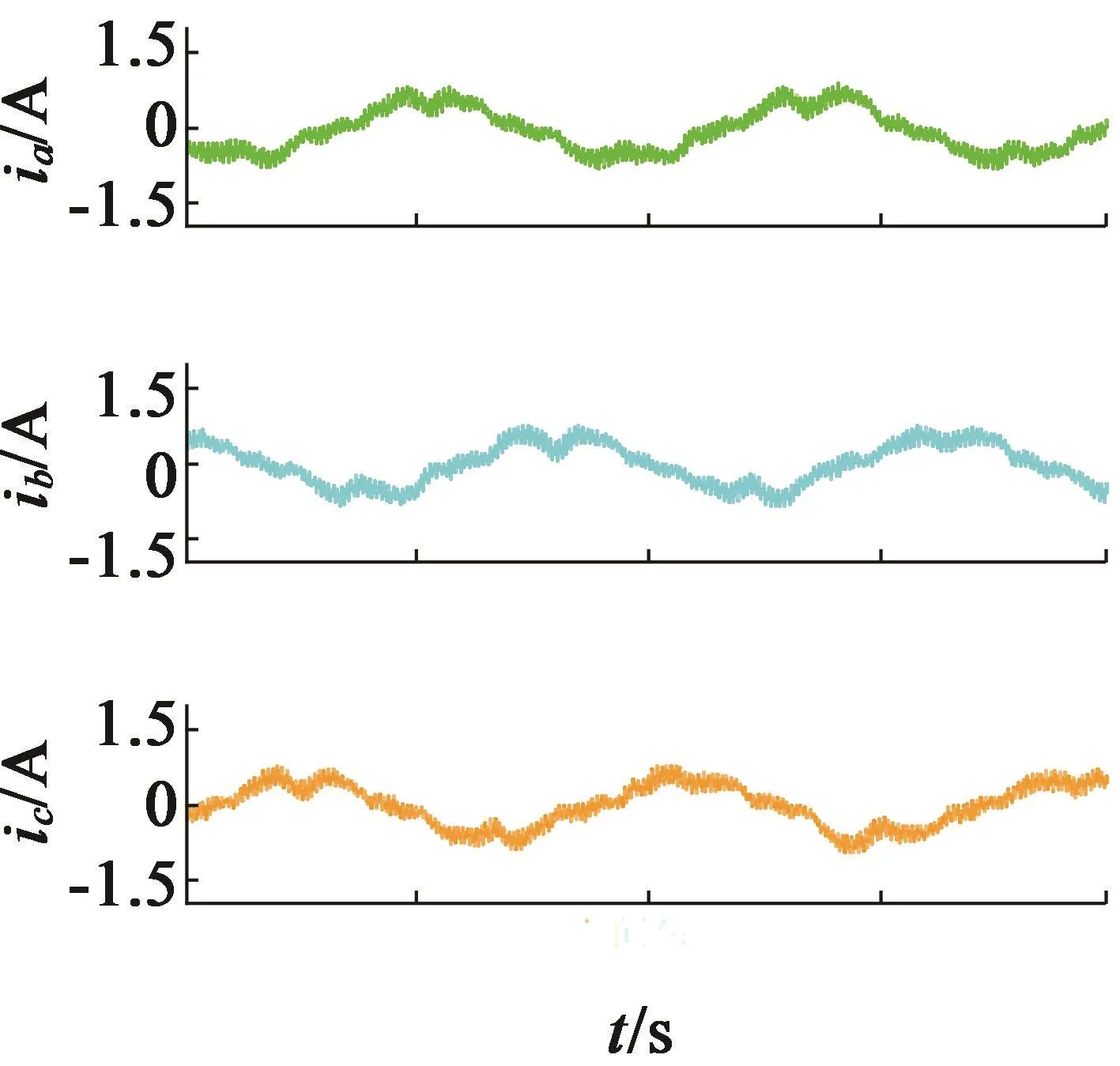
图8 空载电流波形

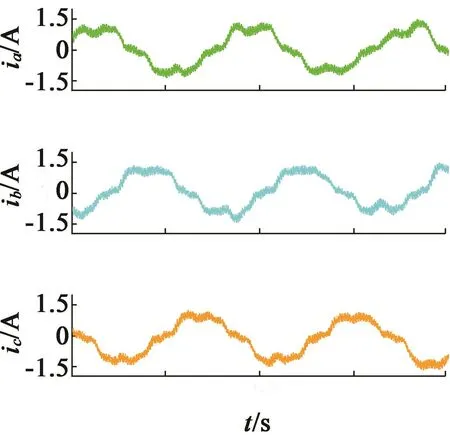
图9 负载电流波形

4 结 语

本文在分析了PMSM和ADRC数学模型的基础上,在转速环和电流环中分别用一阶ADRC来代替PI控制器,设计了基于ADRC的PMSM伺服控制系统,与传统的PID控制相比,在应对突加的系统扰动和带载起动方面,伺服系统的收敛速度更快,静态误差更小,系统的性能得到较大程度的提升。由仿真和实验结果可知,系统对于负载的突变有较强的鲁棒性,稳态和动态时的系统运行都符合理论分析。因此,该模型对PMSM伺服系统的设计具有一定的指导意义。