基于高频信号注入的内置式永磁同步电机电感参数辨识

梅柏杉,张 鹏

(上海电力大学电气工程学院,上海200090)

0 引 言

内置式永磁同步电机(以下简称IPMSM)具有功率密度高、效率高、磁路气隙小、调速范围宽,被广泛用于电动汽车和数控机床等领域[1-2]。

为了能充分利用IPMSM的磁阻转矩,在恒转矩阶段采用最大转矩电流比控制策略,在恒功率阶段采用弱磁控制策略,提高母线电压利用率来达到最大转矩输出。上述控制方法的精度都依赖于电机参数的准确获取[3]。目前,对于永磁体磁链和定子电阻的辨识方法相对成熟,本文主要研究电机交直轴电感的辨识。文献[4]根据考虑饱和效应与交叉耦合影响的电感参数在线估算IPMSM模型,经仿真验证电机运行中电感参数会发生变化。文献[5]提出在不同交直轴电流条件下辨识出对应电感值的方法,但均在电机离线状态下测得,并不能及时跟随电机参数变化。

目前,电机参数常用的在线辨识方法有模型参考自适应法[6]、递推最小二乘法[7]、扩展卡尔曼滤波法[8]等。文献[9]提出用模型参考自适应算法在线辨识电感,需对参数逐个辨识,易引起累计误差,最终结果会有较大偏差。文献[10]采用递推最小二乘法在线辨识电机参数,结构简单,但当参数发生变化时,跟随性差,影响辨识精度。文献[8]提出了永磁电机递归参数在线辨识方法,提高了扩展卡尔曼滤波器无位置控制系统的鲁棒性,但由于模型复杂导致计算量大,跟随性差。

为了进一步改善上述电感辨识策略中存在的跟随性与精度问题,提出基于旋转高频信号注入的电感辨识策略,同时考虑磁路饱和与电感交叉耦合的影响,在此基础上采用串联纯延时滤波器提取高频电流响应,从而得到更为精确的交直轴电感值。此外,采用递推最小二乘法辨识电感值作为对照,仿真结果对基于高频信号注入的电机电感参数辨识策略的可行性和有效性进行了验证。

1 永磁同步电机高频模型

高频注入信号的频率通常为0.5～2 kHz,远远大于电机的基波频率ωr,且大都用于低速甚至零速,反电动势很小,则可以将电机看作一个简单的RL电路。但高频时电阻远小于电抗,常常忽略不计,故考虑磁路饱和与电感交叉耦合时的IPMSM,在高频信号激励下的电压模型[11]可以简化如下:

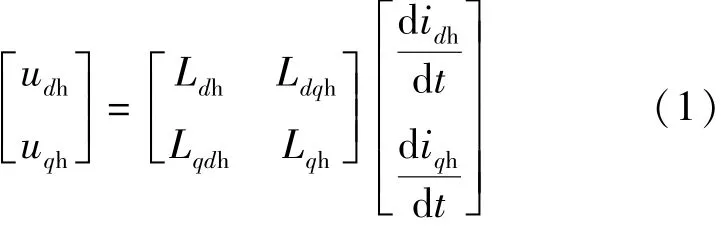
式中:udh,uqh,idh,iqh分别为d,q轴的高频电压、电流分量;Ldh,Lqh分别是d轴和q轴的增量电感;Ldqh,Lqdh表示电机d,q轴受交叉耦合影响的互感分量,由于Ldqh与Lqdh较为接近,故常常令二者相等[12]。根据文献[13]可知,一般情况下Ldqh远小于Ld,Lq,因此在计算中将Ldqh相关项忽略。

IPMSM的d,q轴磁链分别为ψd,ψq,其磁链方程为:

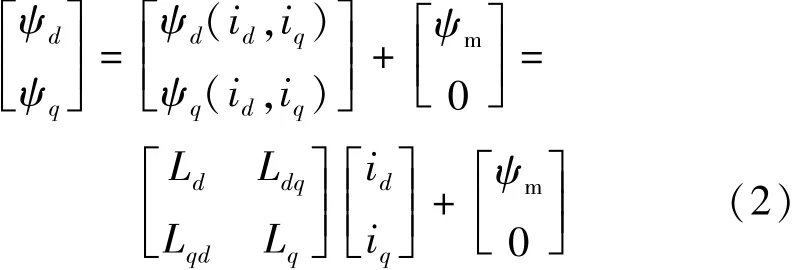
式中:ψd(id,iq),id和ψq(id,iq),iq分别为d,q轴磁链和电流分量;ψm为永磁体磁链。

电磁转矩方程:

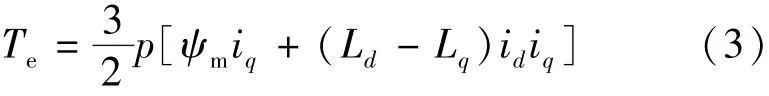
在不同电流作用下,IPMSM中铁磁材料的磁导率将会发生变化,电感参数也不相同,因此通过冻结磁导率(以下简称FPM)[13]的方法获得交直轴自感和交叉耦合互感。定义如下:

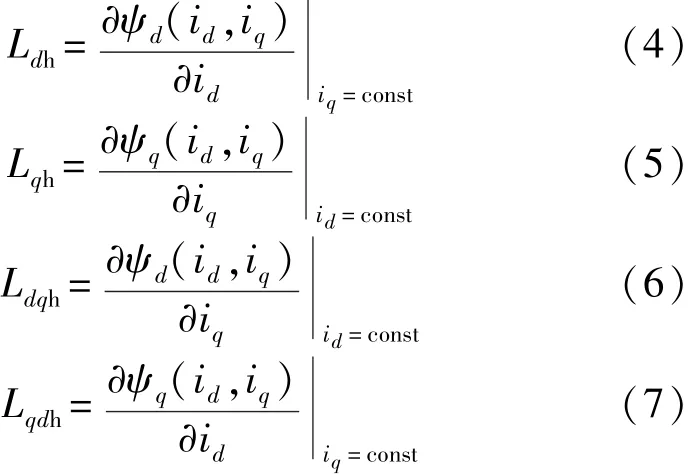
2 注入旋转高频电压辨识d,q轴电感

2.1 旋转高频电压注入法

旋转高频电压注入法是一种常用于凸极率比较大的IPMSM的高频信号注入方法,根据通过注入高频信号、从高频响应电流(或电压)提取出转子位置信息[14]的方法,本文提出了基于旋转高频电压来辨识d,q轴电感的方法。

两相旋转坐标系与两相静止坐标系之间的Park变换矩阵:

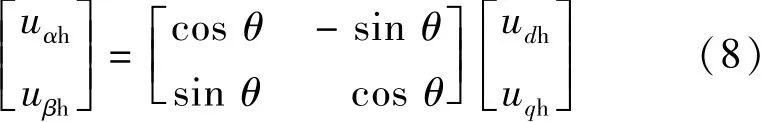
由式(1)、式(8)联立后可得:

假设注入旋转高频电压信号的幅值为Umh,角频率为ωh,则有:

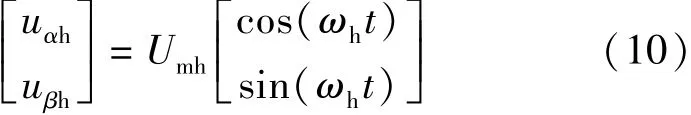
式中:uαh,uβh分别为 α,β轴注入高频电压信号。

综上可得到两相静止坐标系下的高频电流响应:

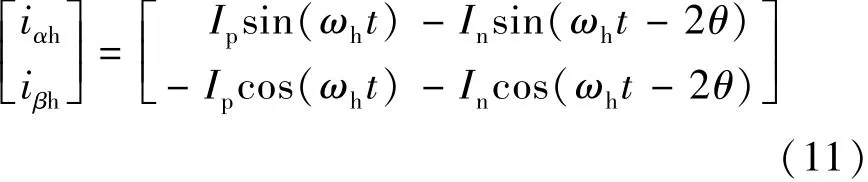
式中:Ip,In分别为高频电流正、负序分量的幅值,且有:

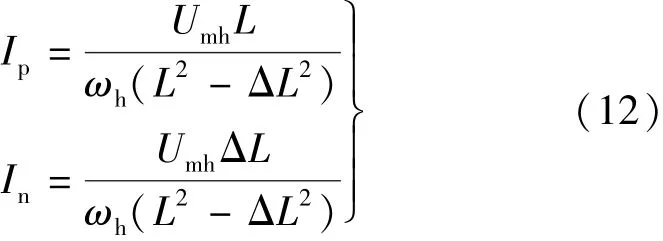
由式(12)可知,Ldh与Lqh的计算公式:

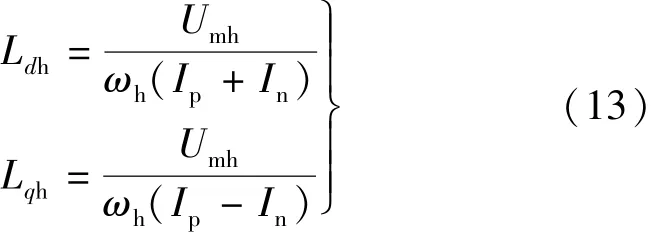
根据上面得到的不同id,iq条件下的Ldh,Lqh,再根据式(2)可得到磁链的计算公式如下:

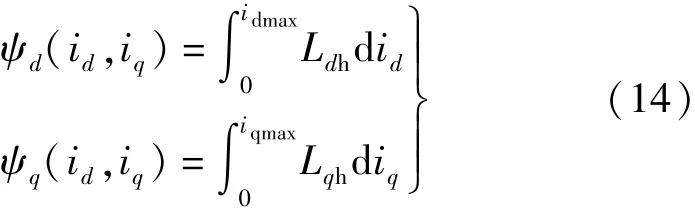
式中:idmax,iqmax分别为id,iq的最大值。

d,q轴静态电感计算公式:

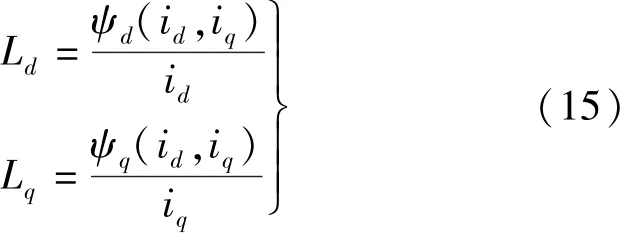
准确辨识Ld,Lq的前提是能够精准获得Ip,In,因此需要对信号做相应的处理,其原理如图1所示,主要环节包括:纯延时滤波器提取高频电流信号、纯延时提取高频电流正负序分量Ip,In。

2.2 纯延时滤波器提取高频电流信号

为了能够获得相对精确的Ip,In,需要有效地滤除电机定子端电流iα和iβ中包含的基波电流、低次谐波电流和PWM开关频率谐波电流,从而提取出由注入的高频电压得到的高频电流响应信号。通常采用常规的带通滤波器(BPF)滤除上述信号,但带通滤波器作用后会导致高频电流信号的幅值发生一定程度上的衰减,进而影响Ip,In的准确度。故本文将采用纯延时滤波器[15]来提取高频电流信号,其原理是将检测到的iα,iβ延迟半个高频电流信号周期τ1(τ1=π/ωh),然后将 iα,iβ与延时后得到的电流信号相减可以得到高频电流。图2位三级纯延时滤波原理图。

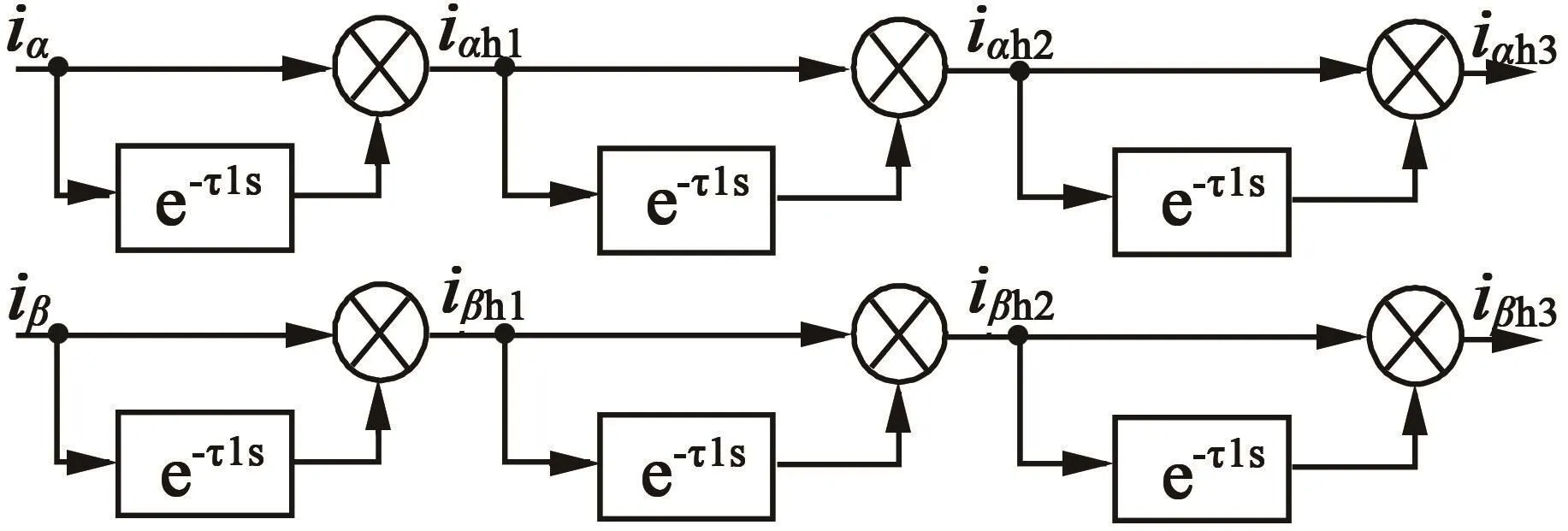
图2 纯延时滤波原理图

检测得到的电机定子端电流:

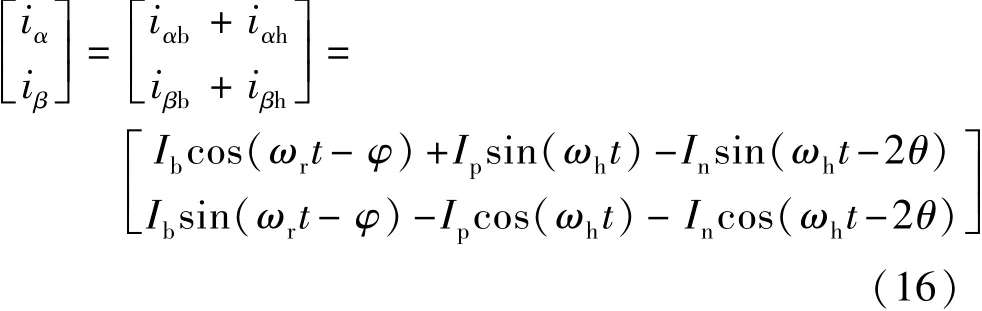
对上式做一次延时处理,可以得到:

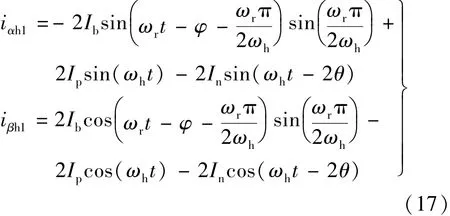
由式(17)可知,经过一次纯延时滤波处理后,高频电流幅值扩大了一倍,但基波信号降为原来的倍,又由于高频信号频率 ω 远远高于基h波信号频率很小,故认为基波电流可以较大程度上被滤除。分析线路中流经的电流频率,为了增强滤波效果,按照上述方法对 iαh1,iβh1再进行两次纯延时滤波处理后,便可得到:

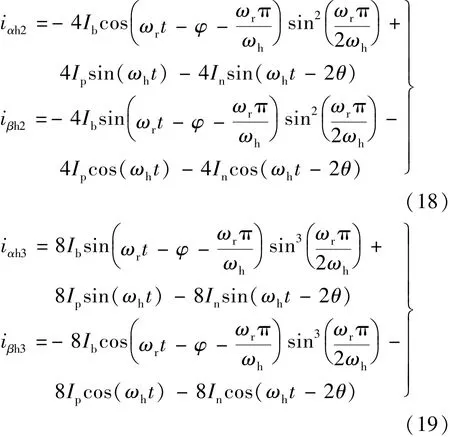
由式(19)可知,通过三级纯延时滤波器处理后,高频电流信号扩大为原来的8倍,更利于后面信号的处理过程,基波电流幅值减小为原来的此时可以认为基波信号已基本完全消除。故可知高频电流:

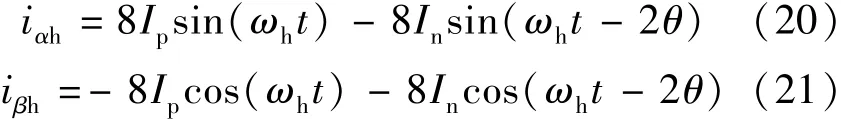
2.3 纯延时提取高频电流正负序分量Ip,In

将高频信号iαh,iβh作延时四分之一个高频信号周期处理,经简单运算后可以得到:

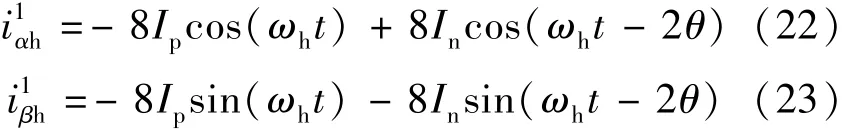
将式(20)～式(23)联立后做简单的加减运算可以得到:

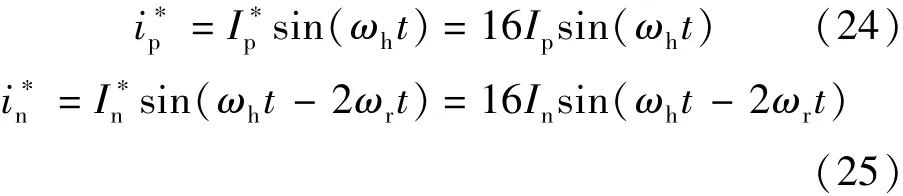
根据上面的推导过程可知,iαh,iβh经延时并运算处理后,得到两个幅值分别为频率分别为的正弦信号。对进行傅里叶分析,可以得到较为精确的

综上可知,纯延时滤波器能通过注入较小的高频电压信号得到较大的高频电流信号,对高频电流信号处理得到两个标准的正弦信号,从而得到较为精确的Ip,In。

3 仿真验证

为了验证本文提出的基于高频信号注入的电感参数辨识方法的有效性,进行了仿真验证。表1为仿真时使用的电机具体参数。注入的旋转高频电压信号幅值Umh为1 V,角速度ωh为2 000π rad/s。

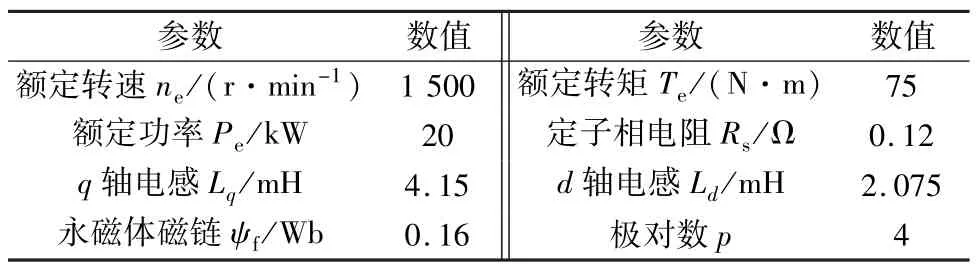
表1 电机参数

仿真时长设定为1 s,t=0.2 s时,d轴电流由-6 A阶跃至-3 A。Ld,Lq的初始值分别为2.075 mH,4.15 mH,模拟电机在实际运行过程中电感参数发生变化的情况,在仿真进行至0.5 s时,Ld突变为2.03 mH,仿真进行至0.7 s时,Lq突变为4.07 mH。

图3为测量电流经过纯延时滤波器后提取出的高频响应电流,从图4中可以看出,其他频率的幅值与iαh的幅值相比都较小,可认为基波与其他频率的谐波已基本滤除,与理论分析结果一致,有效提取出了高频电流信号。

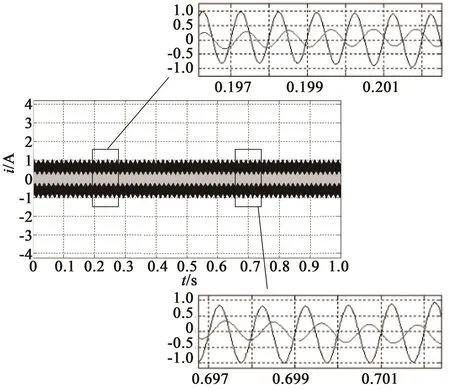
图3 高频响应电流经延时处理后波形

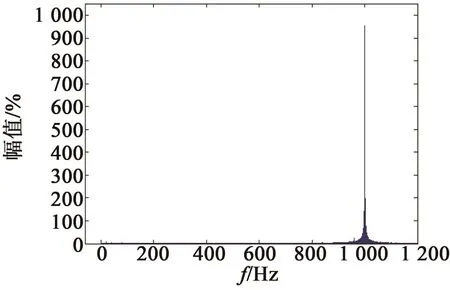
图4 纯延时滤波器提取的iαh傅里叶分析

本文基于高频信号注入法的电感辨识结果如图5所示。由图5可知,d轴电感辨识误差为0.98%,q轴电感辨识误差为0.73%。采用文献[7]中的递推最小二乘法在线辨识电机电感参数,辨识结果如图6所示,电感参数发生变化时,辨识结果的跟随性稍差,d轴电感辨识误差为1.47%,q轴电感辨识误差为2.21%。分析图5、图6可知,本文基于高频信号注入的电机电感参数在线辨识策略具有较好的跟随性与精度,整个辨识过程鲁棒性较强,能实现电感参数的在线辨识。

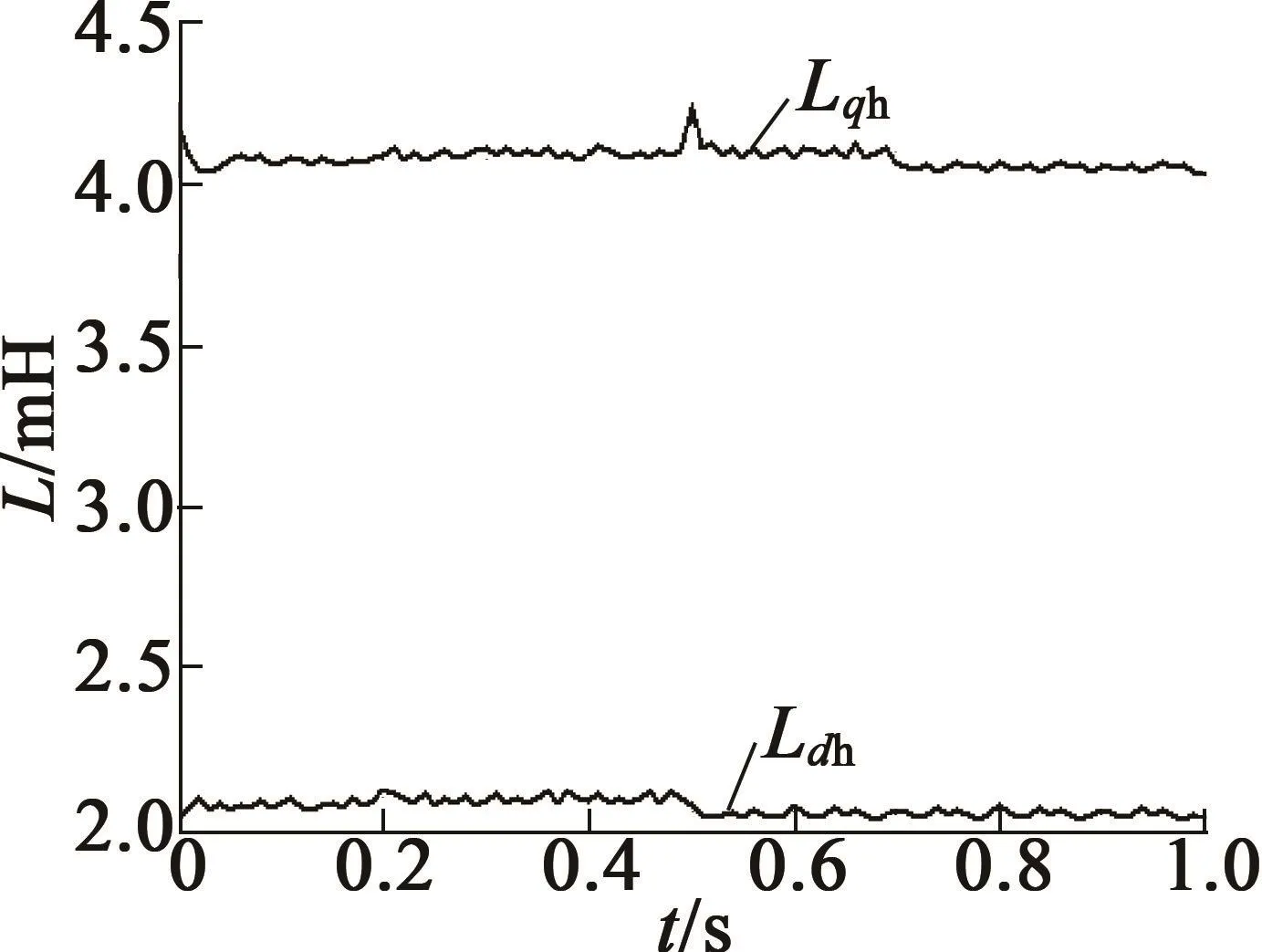
图5 dq轴电感在线辨识结果

4 结 语

本文针对电感辨识策略中跟随性和精度问题,提出了一种基于高频信号注入的电机电感参数在线辨识策略,实现了交直轴电感值的辨识,并对控制策略的可行性与有效性进行了验证,仿真结果表明:

1)通过纯延时滤波器提取出高频电流信号,获得较好的处理效果,通过高频信号的无相位延迟处理,提高了高频信号的信噪比,从而得到更为精确的交直轴电感值。

2)参数发生变化时,基于高频信号注入的电感参数辨识策略有较好的跟随性与精度,避免因参数变化对电机控制精度和可靠性产生影响,提高了系统的鲁棒性。