基于磁共能重构的电励磁同步电机分布参数建模方法

尹 星,钟再敏,周水华,李俊杰

(同济大学 汽车学院,上海201804)

0 引 言

电励磁同步电机(以下简称EESM)由于其功率因数可调、过载能力强、效率高等特点[1],现被广泛应用在车用电驱动系统中。准确的电机模型是车用电机精确控制的前提,然而,电机在运行过程中,由于其非线性特性与谐波特性,难以得到准确的电机数学模型。

传统的基于集中参数的电机数学模型,是在假设气隙磁场呈正弦分布和不考虑转子铁心饱和的情况下,得到了较为简洁的电机数学模型。但其忽视了电感参数会随着空间位置发生变化的情况,不能准确描述电机运行过程中的非线性特性和谐波特性,难以实现对电机的精确控制[2]。

为精确考虑电机运行过程中的谐波和非线性特性,实现对电机磁场情况的准确描述[3],本文研究了一种基于磁共能重构的EESM分布参数建模方法。由于EESM存在转子励磁绕组,与永磁体励磁的永磁同步电机相比,其需要更多的参数来表征磁共能在空间上的分布情况,主要体现在分布参数矩阵Ck的维度上;同时,转子侧变量的引入,使得整个分布参数建模方法较永磁同步电机更复杂,但其整体建模思路与永磁同步电机类似。

首先,根据磁共能在转子位置θr及转矩角β两个维度上的周期性,运用二维傅里叶级数展开及二元多项式拟合,得到了以分布参数矩阵Ck表示的磁共能模型;然后,根据所重构的磁共能模型,建立相应的转矩、磁链以及定子电压解析模型;最后,通过在变工况情况下进行的准确性验证,证明了所建立的分布参数电机模型在描述电机转矩、磁链谐波特性方面的准确性,为基于模型的电机控制提供了理论基础。

1 基于有限元数值分析的磁共能重构模型

1.1 EESM有限元模型仿真

为实现对电机磁场情况的准确描述,有限元数值分析(以下简称FEA)被广泛应用于电机设计中。本文以某款EESM为研究对象,建立其FEA仿真模型,一方面通过FEA仿真获取其在各个不同工况点下精确的磁共能数值,并用于后续的重构磁共能建模;另一方面通过FEA仿真所得的电磁转矩、磁链及电压数值解,可对所构建的EESM分布参数模型的准确性进行验证。建立四分之一EESM有限元模型,如图1所示,相关设计参数如表1所示。

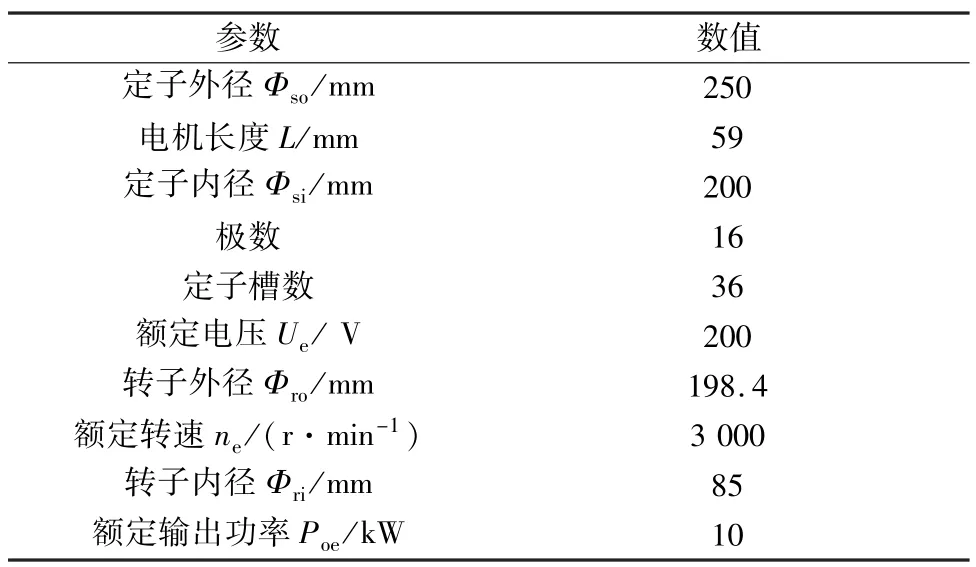
表1 EESM相关设计参数

图1 二维EESM四分之一FEA模型

本文利用Maxwell软件可直接获得电机磁共能数据,对于其他有限元软件,磁共能数据可能不能直接获得。因此,可以依据式(1),由定子d-q轴磁链及转子励磁等效磁链积分获得磁共能数据。

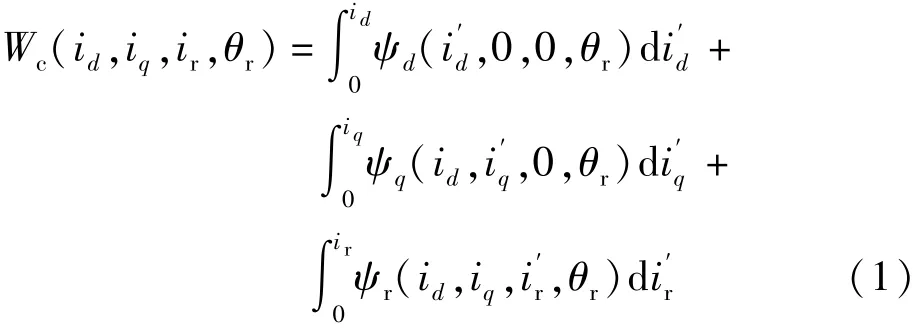
1.2 磁共能的二维傅里叶级数展开

对于Y型绕组连接的电机,在三相对称正弦电流激励下,d-q轴磁链中仅含有6、12、18、24等6k次谐波[4-5]。根据磁链积分可得磁共能数据,易推得EESM的磁共能也仅含有6k次谐波。

图2展示的是定子电流Is=10 A,转子励磁电流Ir=3 A时磁共能的分布图。图2(a)表示的是磁共能在θr与β两个维度上的分布图,图2(b)为固定θr下,磁共能随着β值的变化结果,图2(c)则为固定β下,磁共能值随着θr的变化结果。从图2中可以看出Wc在β及θr维度上均具有周期性,且其基波周期分别为2π与π/3。

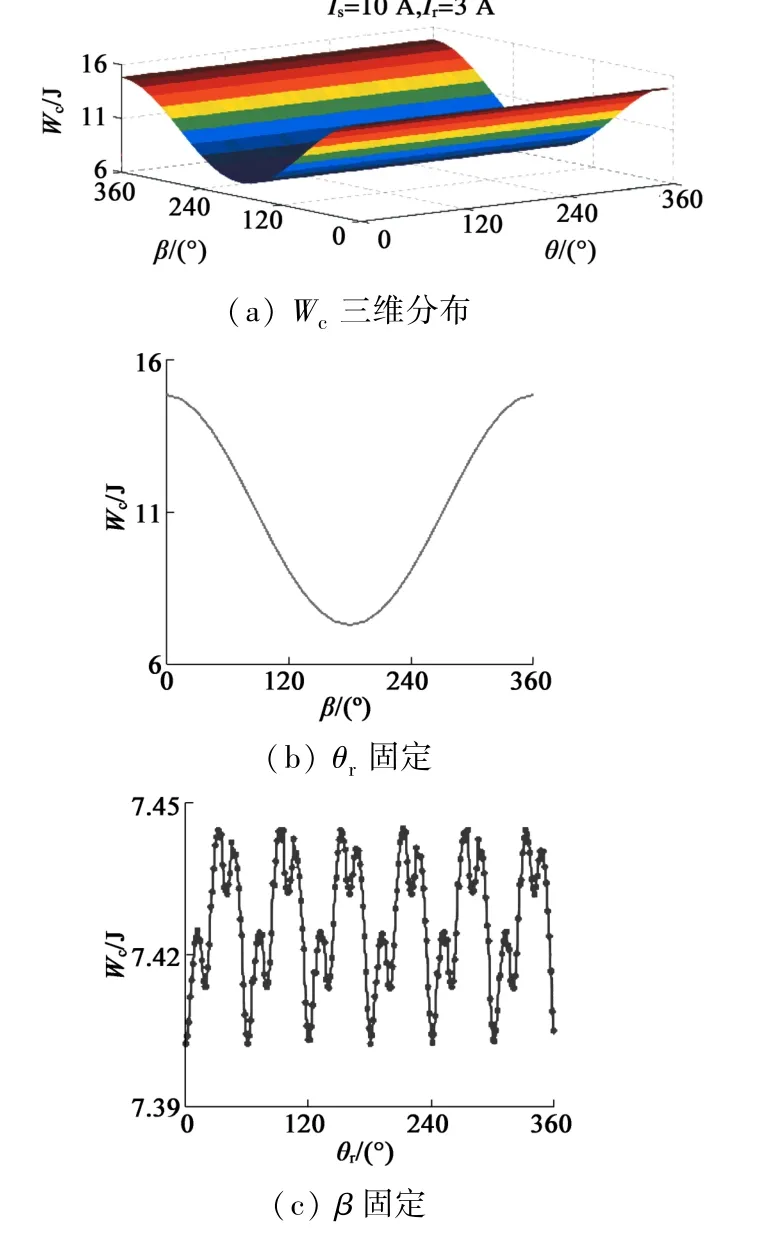
图2 EESM磁共能数值解分布图

因此,根据Wc在θr及β两个维度上的周期性,对特定(Is,Ir)下的所有磁共能数值解Wc(θr,β)进行二维傅里叶级数展开,如下:

式中:Gm1,m2为当θr及β维度的阶数分别为m1与m2时所对应的傅里叶级数系数;ωθ为磁共能在θr维度上的角频率;ωβ为磁共能在β维度上的角频率。

对于真实的电机系统,其磁共能主要集中在其基波及低次谐波中,因此,式(2)中的傅里叶级数阶数可以缩小到有限次。改进后的磁共能表达式如下:

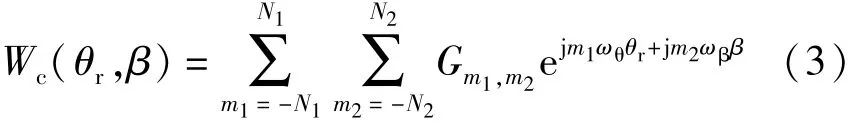
式中:N1及N2分别为设定的磁共能在θr及β维度上傅里叶级数的最高阶次。

1.3 傅里叶系数的二元多项式拟合

式(3)仅能描述Is,Ir为固定值时磁共能随θr及β的变化规律,但不能表述出磁共能随Is和Ir的变化规律。实际电机运行过程中,当Is和Ir增加时,EESM的磁饱和程度会加剧,从而导致电机电磁特性及磁共能随θr及β的变化规律发生改变。在此,通过描述傅里叶级数系数Gm1,m2随Is,Ir的变化,即可表征Wc随Is,Ir的变化规律。

为了将 Gm1,m2表示为 Is,Ir的函数 Cm1,m2(Is,Ir),同时考虑到电机运行时复杂的非线性特性,本文将其形式选为Is,Ir的高阶二元多项式,如下:

式中:N3为所选择的二元多项式最高阶次。此时,Wc与Is,Ir的关系可表示:

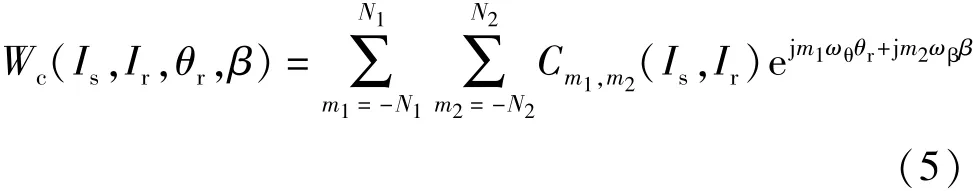
将各个Cm1,m2(Is,Ir)函数合并到一个矩阵函数C(Is,Ir)。同时,为简化表达式,将各阶傅里叶级数记为向量的形式:

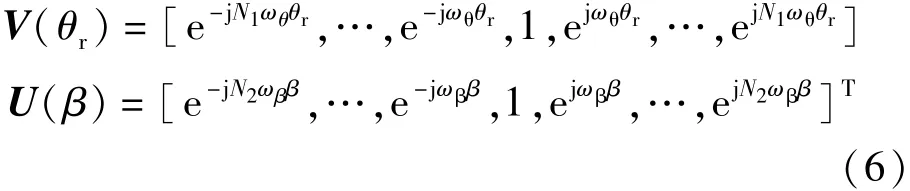
最终,重构的磁共能表达式如下:

该表达式由三部分组成,其各自表征了Wc在(Is,Ir),θr及 β四个维度上的变化规律。其中V(θr)为在θr维度上选取的傅里叶级数基底,其最高阶次为N1,其可描述的θr维度上的最高次谐波为6N1次;U(β)为在β维度上选取的傅里叶级数基底,其最高阶次N2同样代表着在β维度上描述磁共能谐波的能力;C(Is,Ir)为描述磁共能随(Is,Ir)变化的矩阵函数,该矩阵函数元素为二元多项式,各不同项前面的系数Cij为维数为(2N2+1)×(2N1+1)的矩阵。在本文中将Cij称为“分布参数矩阵”。实际应用中,可依据电机本身的特性及应用需求合理调整二维傅里叶级数或多项式拟合的维度大小,以保证模型的准确性与复杂性之间的平衡。

2 基于重构磁共能的EESM分布参数电机模型

2.1 电磁转矩模型

根据虚位移原理[6],利用重构的磁共能对转子位置求偏导,可得电磁转矩的表达式:

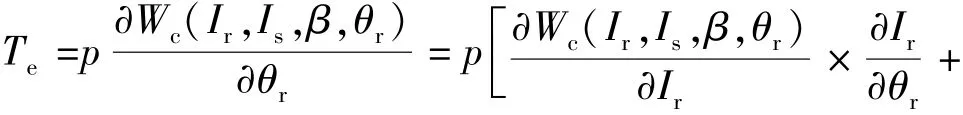
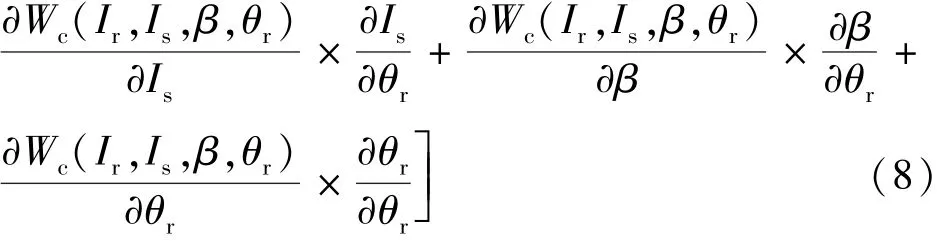
式中:

最终,代入各表达式,可得基于分布参数模型的电

磁转矩解析模型:

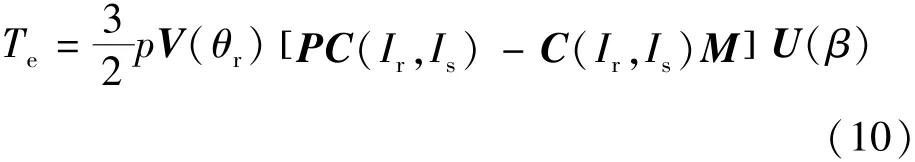
式中:

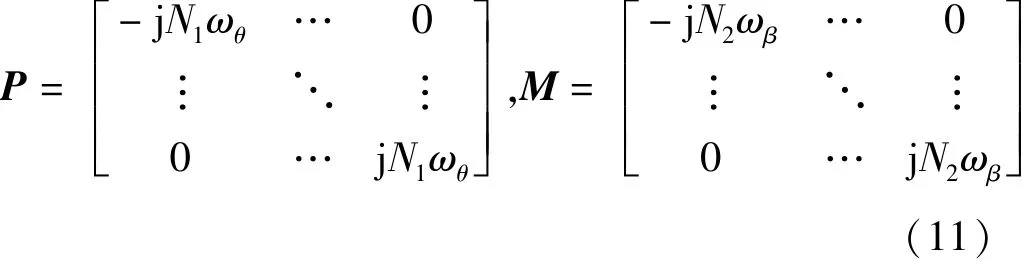
2.2 磁链模型

磁共能对定子d-q轴电流的偏导,即为d-q轴等效绕组上交链通过的磁链,以 d轴电流为例,其对应的定子磁链ψd与所重构磁共能之间的关系如下:

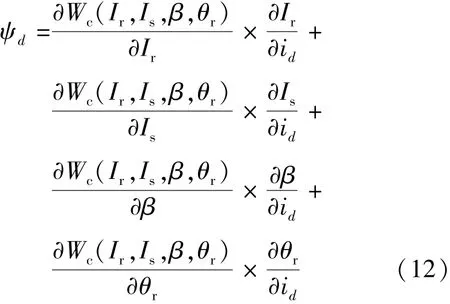
式中:

整理可得d轴定子磁链解析表达式:

同理,可得q轴定子磁链解析表达式:

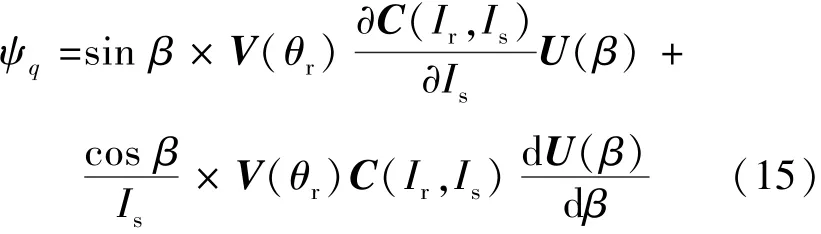
转子磁链ψf可由磁共能Wc对Ir求偏导得到:修正为

Ir的幅值由外界激励给定,与Is,β,θr无关,即有,代入可得转子磁链解析表达式:

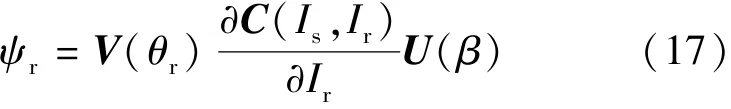
式(15)和式(16)的分母中均含有Is项,当定子电流激励为0时,C(Is,Ir)中的C0j项会使磁链的计算结果无穷大。而C0j项表征的是转子励磁线圈本身自感产生的磁共能,该部分磁共能并不会在dq轴等效绕组中产生磁链,即其不会影响d-q轴磁链的变化。

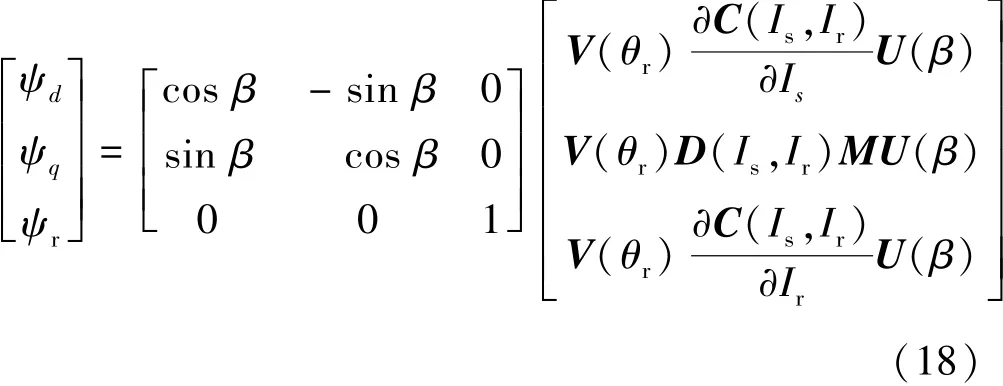
2.3 电压方程

由定子磁链解析模型可得M-T同步旋转坐标系下的定子磁链:

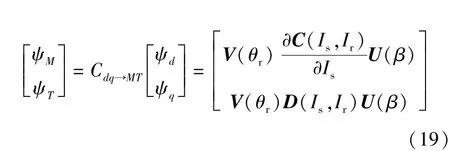
M-T同步坐标系下的磁链表达形式要比d-q同步坐标系下的磁链表达式简单,因此下文将基于M-T同步旋转坐标系来建立EESM的电压方程。由定义可知,电流矢量Is在M轴上的分量即为定子电流矢量幅值Is,而在 T轴上的分量为0,即iM=Is,iT=0。可得M-T同步坐标系下定子侧的电压矢量方程:

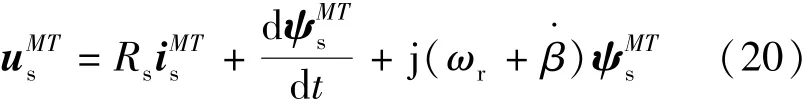
代入之前获得的磁链解析模型,整理可得M-T坐标系下的定子侧电压方程解析模型:式中:

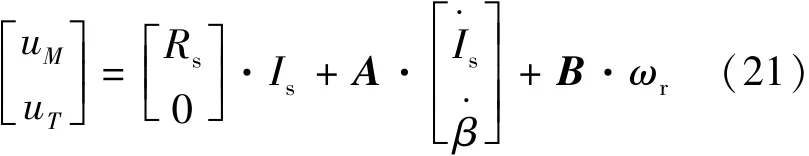
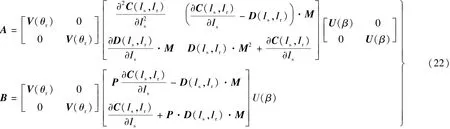
同理,转子侧电压方程的矢量形式可表示:

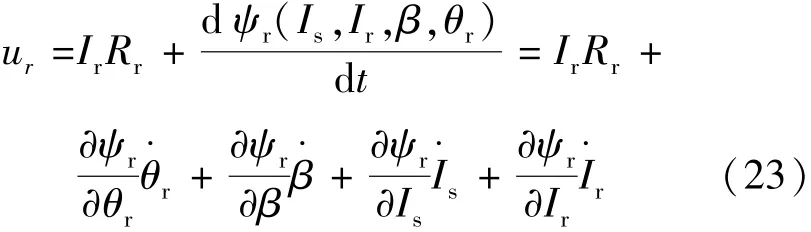
代入转子磁链解析模型,可得转子电压方程解析模型:

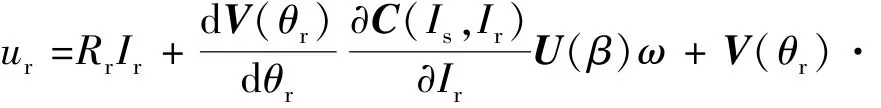
3 分布参数模型与FEA比较

为了验证所建立的EESM分布参数模型的准确性,在定子为谐波电流激励和转子电流变化时对比分布参数模型与FEA模型的结果。仿真时,在定子三相电流中加入5、7次谐波,如图3所示。

同时,转子电流也不再设为恒定值,而是加入一个正弦波扰动,转子电流Ir=Ir0+Ir1cos(2πft),仿真时,设置Ir0=2 A,Ir1=0.1 A,f=50 Hz,转子电流激励如图4所示。

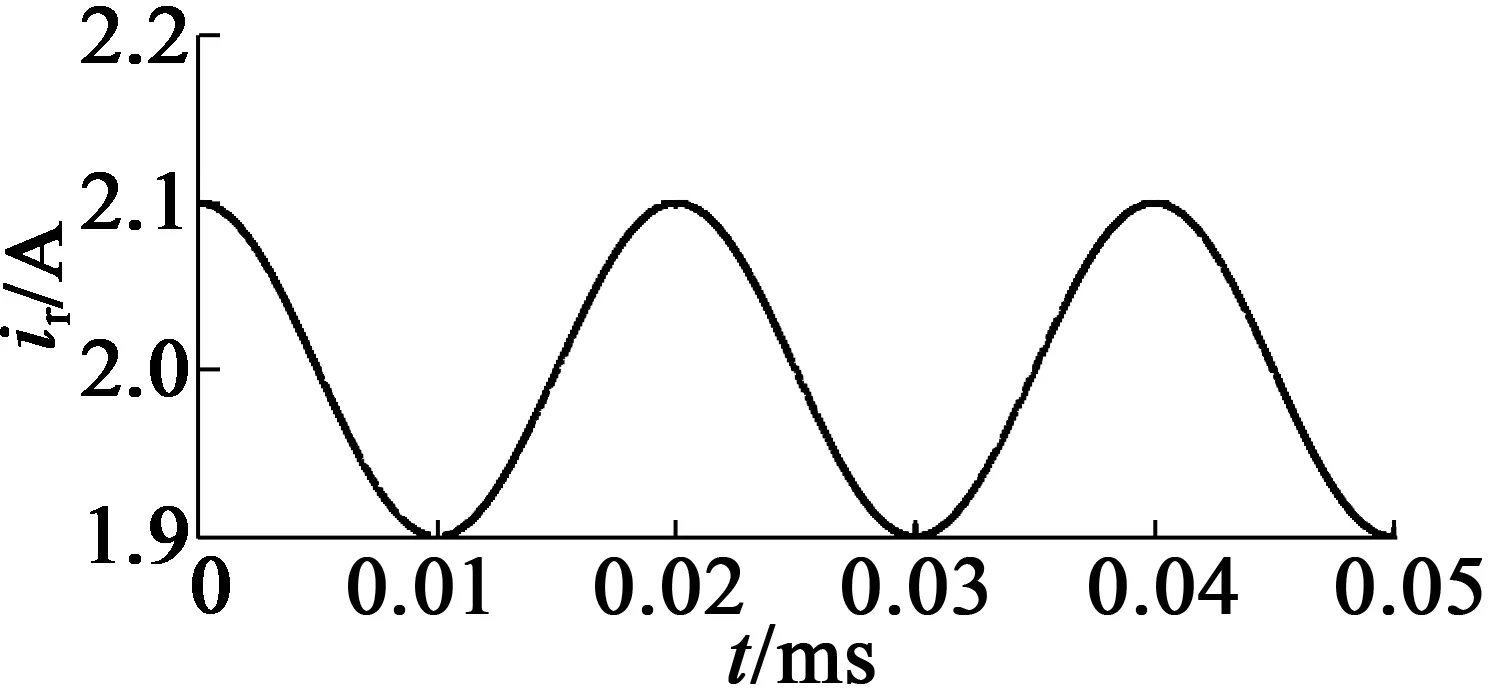
图4 转子电流激励

图5 为所建立的分布参数电机模型与FEA模型的比较结果,包括磁共能、转矩、定子d-q轴磁链、转子磁链、定子M-T轴电压和转子电压的对比。

从图5中可看出,分布式参数电机模型得到的各数据结果同FEA所得结果之间的吻合程度较高,基本证明了所建立的EESM分布参数模型可以充分描述电机在各种工况下的运行状态,为基于模型的电机控制提供了理论基础。

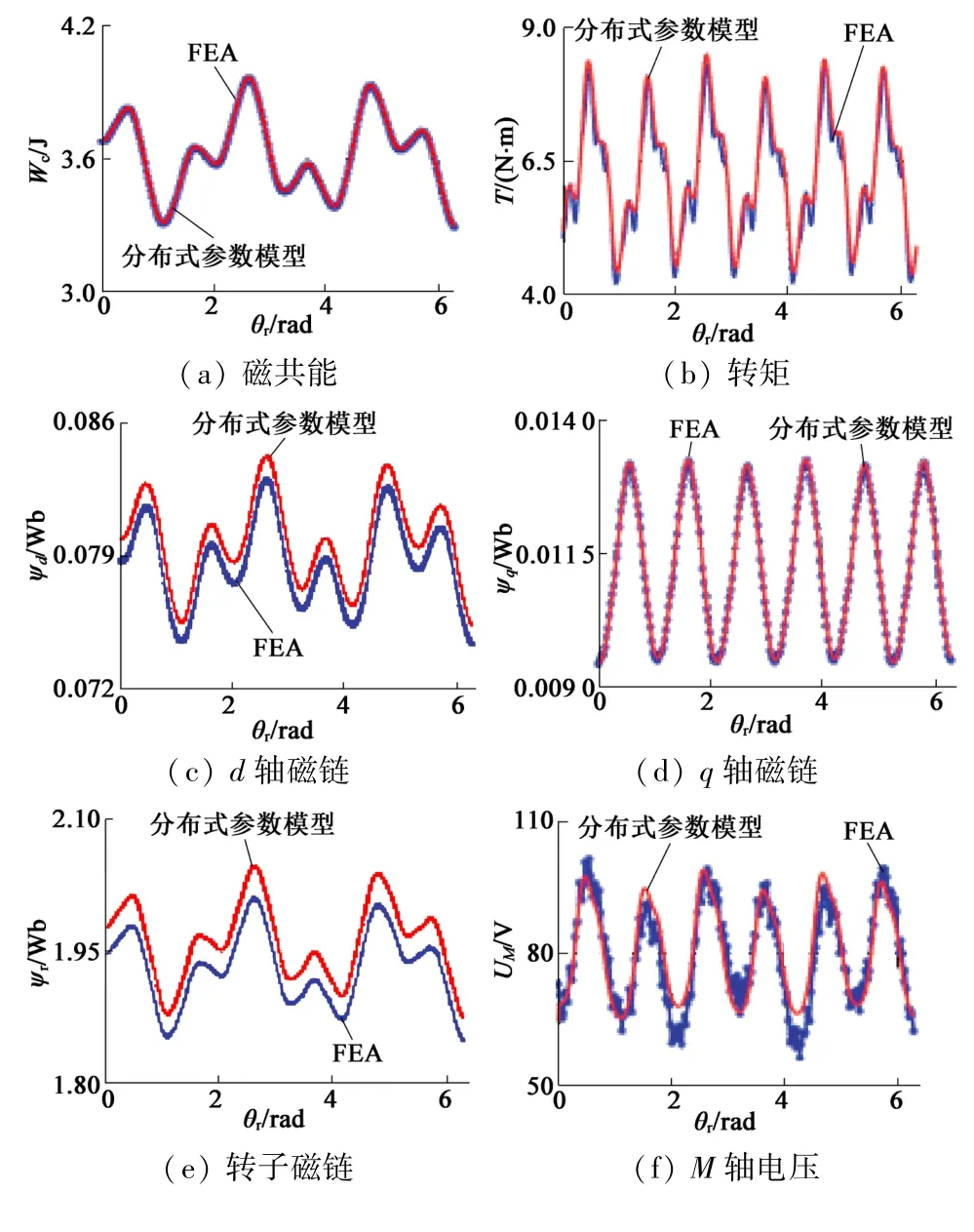
图5 Is=10 A,Ir=2 A,β =135°时分布参数模型与有限元模型的对比结果

4 结 语

本文利用FEA所得电机的磁共能数据,利用二维傅里叶级数展开和多项式拟合对磁共能数值解进行了重构,获得了EESM的分布参数电机模型。经对比验证,所构建的分布参数电机模型与FEA所得数据具有良好的一致性,证明了分布参数电机模型能充分描述电机在运行过程中的非线性特性与谐波特性,对基于模型的电机控制技术有重要的参考价值。