考虑驱动器参数的混合式步进电动机精细化模型

李听斌,李卓航,朱 亮,朱加贝,章 懰,杜一东,戚振亚,周奇慧,吴立建

(1.中国电子科技集团公司第二十一研究所,上海200233;2.浙江大学电气工程学院,杭州310027)

0 引 言

步进电动机是一种开环控制、精确定位的电机,在工业中有着不可替代的作用。步进电动机控制系统采用开环控制,对于硬件和软件的要求较低,但是开环控制会造成步进电动机的各种控制问题,如失步故障、越步故障等。建立一个精确的步进电动机系统模型对于分析步进电动机运行性能,改进步进电动机控制算法具有重要意义。

步进电动机系统包括步进电动机本体、步进电动机驱动器和控制器三大部分。在传统的步进电动机建模中,针对步进电动机本体建模做了很多工作,文献[1]对多相混合式步进电动机做了线性解析,没有考虑铁心饱和对电机参数的影响。铁心饱和造成的电机参数非线性特性对于电机性能影响较大,为了提高步进电动机模型的精确性,文献[2-4]将电机中的电感和电势系数等参数的非线性特性引入电机模型中,推导出了比较完善的非线性电感和电势系数公式。在此基础上,文献[5]建立了二相混合式步进电动机本体的非线性模型,但需要获得的参数量较多,且对较难获得的电感参数依赖性较大。此外,在步进电动机驱动器中,功率器件的开关方式、导通电阻以及续流二极管对步进电动机的运行性能具有重要影响。文献[6]研究了步进电动机系统线性仿真模型,建立了混合式步进电动机与驱动器的耦合模型,该模型参数为常数,精确度较低。

本文建立了一种考虑驱动器参数的两相混合式步进电动机精细化模型,包括混合式步进电动机本体模型以及两相的驱动器模型。在混合式步进电动机本体模型中,充分考虑了铁心饱和造成的非线性影响,获得受电流影响的电感参数、旋转电压系数和转矩系数,并将这些系数的非线性特性用衰减系数表示,简化了电压平衡方程与转矩方程。电机参数可以用解析法、有限元法或实验法等方法得到。同时考虑了旋转电压等系数的高次谐波,进一步提高模型精确度。本文考虑了驱动器中的功率器件导通电阻和二极管压降对电机运行性能的影响,结合了步进电动机本体模型和驱动器模型,将步进电动机建模从步进电动机本体扩展到步进电动机系统。并考察步进电动机系统中的参数敏感度,分析参数对模型精确度的影响,通过实验与仿真结果对比,验证了模型的精确性。

1 步进电动机建模

1.1 电压平衡方程与机械方程

本文研究的步进电动机为两相混合型步进电动机,该电机磁场由转子上的永磁体和定子电枢电流产生,其电压平衡方程可表示[5]:

式中:ua和ub分别为A相和B相绕组的相电压;ia和ib分别为A相和B相绕组的相电流;ψa和ψb分别为A相和B相绕组的磁链;Rs为相电阻;Lsa和Lsb为A相和B相绕组自感;Lm为两相之间的互感;ea和eb分别为A相和B相绕组的旋转电压。磁链和旋转电压的表达式如下[5]:

式中:ψaa和ψbb分别为A相和B相绕组的自感磁链;ψab和ψba为A相和B相绕组之间的互感磁链;ψfa和ψfb为A相和B相绕组匝链的永磁磁链。

旋转电压包括永磁磁链产生的反电动势以及电感随转子位置角变化导致的绕组磁链变化产生的电势。由旋转电压、相电流和转速计算可以得到电磁转矩:

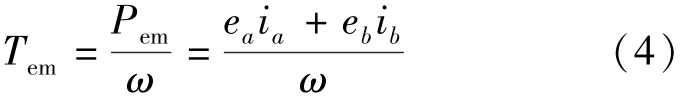
式中:Pem为电磁功率。

步进电动机机械运动方程可以表示为如下形式:

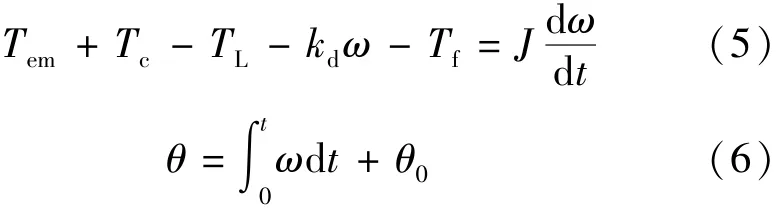
式中:Tem为电磁转矩;Tc为自定位力矩;TL为负载转矩;Tf为摩擦力矩;kd为阻尼系数;θ为转子机械位置角;ω为转子机械角速度;θ0为转子初始位置角。转子位置的零位定义为A相绕组单相通电时转子的平衡位置。

由于电机铁心的饱和效应,当电机绕组电流变化时,电感、旋转电压和电磁转矩会呈现出非线性变化。为了考虑电机参数的非线性特性,提高模型的精确性,本文用衰减系数表示这些参数的非线性特性,衰减系数可通过解析法、有限元法或实验法得到。为了方便起见,本文采用了实验测量的方法得到衰减系数。

1.2 电感非线性

在步进电动机的非线性分析中,电感可以视作绕组电流和转子位置角的函数,其中铁心饱和引起的电感非线性可由衰减系数kL来表示。因此,电感可以表示为衰减系数与线性电感的乘积:

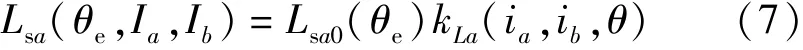
式中:Lsa为A相自感;kLa为A相自感衰减系数;θe为转子位置的电角度,与机械角度θ关系如下:

式中:Nr为转子齿数。

1.2.1 电感与转子位置角的关系

本节分析电感与转子位置角的函数关系,得到不考虑铁心饱和效应时的电感表达式。

运用磁网络模型法,忽略气隙磁导的2次及以上高次谐波分量、定子极间漏磁以及绕组端部漏磁,可得不考虑非线性特性时两相混合式步进电动机的自感[8]:

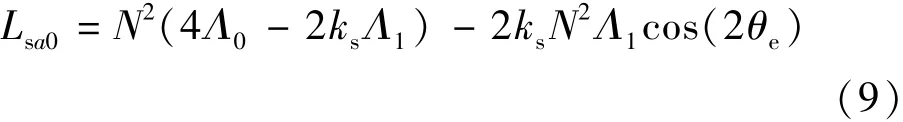
式中:N为绕组匝数;Λ0和Λ1为气隙磁导的直流分量和基波分量幅值;ks表示转子位置角为0时,A相作用在轴向励磁回路的系数,其表达式[8]:

式中:Λm为永磁体内部磁导。

B相自感与A相自感幅值相同,但在相位上滞后A相90°电角度。B相自感表达式如下[8]:

步进电动机的相间互感可表示为如下形式[8]:

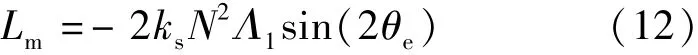
混合式步进电动机由于转子上有轴向充磁的永磁体,A相绕组电流引起随转角变化的轴向磁通分量,在永磁体内部磁阻上的磁压降,相当于加在各磁极支路上的去磁磁势。在B相磁极支路中产生了磁通分量,体现了B相与A相绕组的磁耦合和互感[8]。由于两相存在磁耦合,在下文分析衰减系数的时候都需要考虑邻相电流的影响。

在建立自感的解析表达式时,由于忽略了气隙磁导的高频分量,所得自感由直流分量和基波的二倍频分量组成。固定B相电流为0,变化转子位置角,采用法可以得到对应转子位置角下的不同A相电流的自感值,当A相电流为0时,可以得到自感随转子位置角的变化关系,如图1所示。实测自感含有2次以上高频谐波分量。对比之前的理论推导,对实测自感值做傅里叶分解,只保留自感的基波和2次谐波分量。

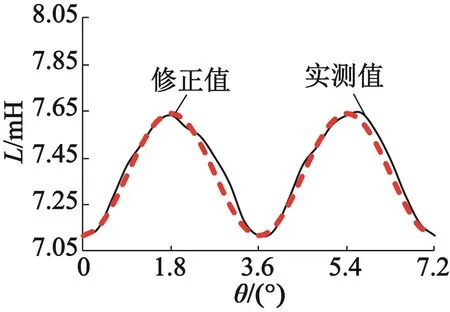
图1 A相自感随转子位置角的变化

1.2.2 电感与电流大小的关系

当A相电流较小时,铁心的饱和程度较低,铁心磁导率随A相电流变化不明显,因此A相自感基本不变。当A相电流较大时,铁心饱和程度增加,铁心磁导率明显减小。由于永磁体磁场存在,在不同转子位置角,A相电流对磁路的影响表现为去磁效应或增磁效应,对电感的影响也不相同。由式(7)可知,不同相电流下得到的实测电感值与相电流为0时的电感值之比为对应相电流下的电感衰减系数。图2为B相电流为0时,转子位置角与A相电流对电感衰减系数的影响。

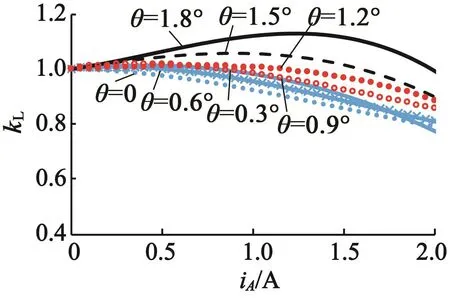
图2 转子位置角对电感衰减系数的影响

通过前面的分析可知,B相电流会影响A相电感衰减系数,以转子位置角θ=0.9°时为例,图3为B相电流对A相电感衰减系数的影响。在不同的B相电流下得到转子位置角和A相电流的影响,可以得到综合的电感衰减系数kL(ia,ib,θ)。

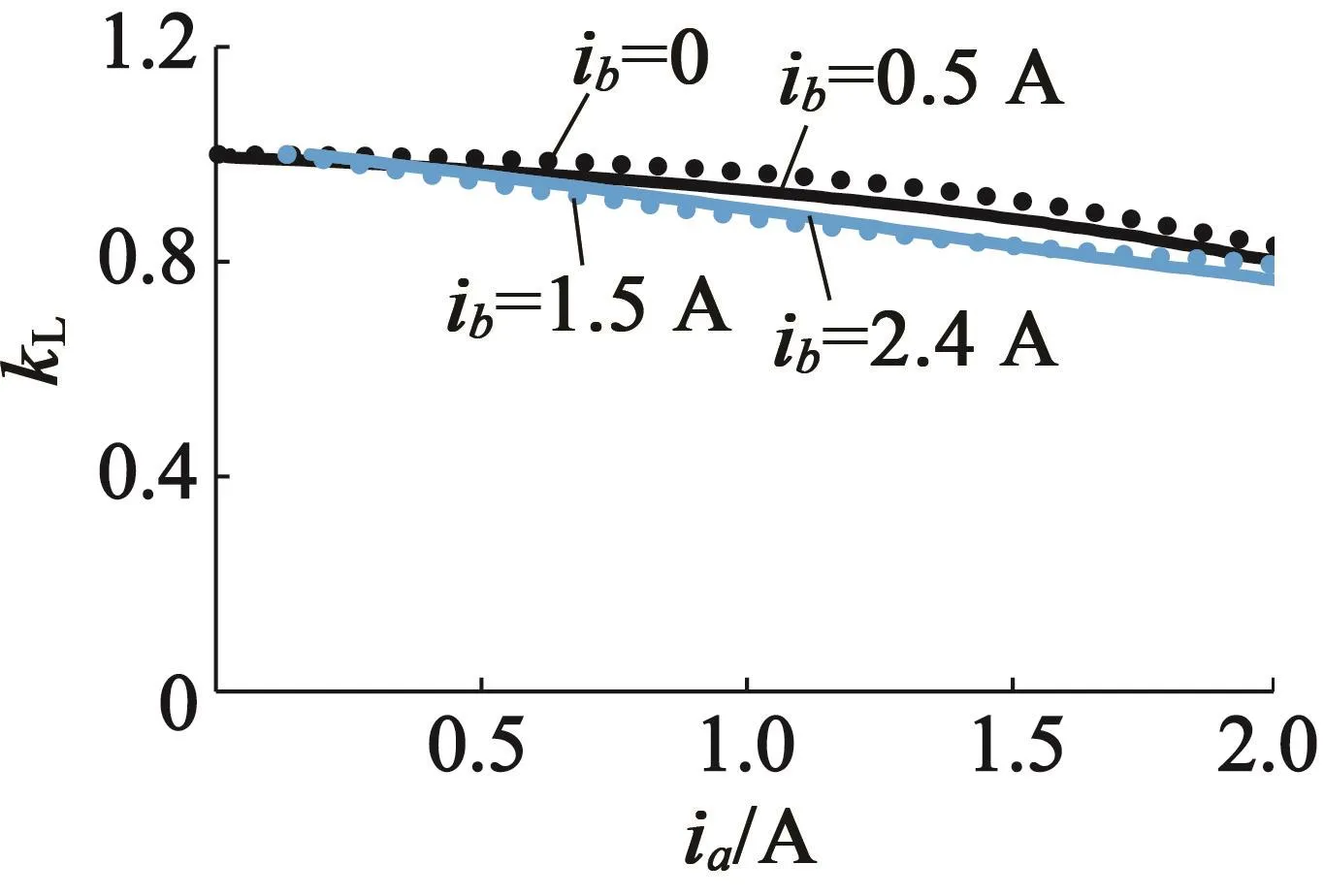
图3 B相电流对电感衰减系数的影响

由于绕组结构的对称性,B相自感波形与A相自感波形相同,但在相位上滞后A相90°电角度,对应A相绕组的自感衰减系数,可以得到B相绕组的自感衰减系数。

1.3 旋转电压与电磁转矩非线性

1.3.1 无电枢反应的旋转电压与电磁转矩系数

由电压平衡方程可知,步进电动机的旋转电压与转子转速之间存在如下关系:

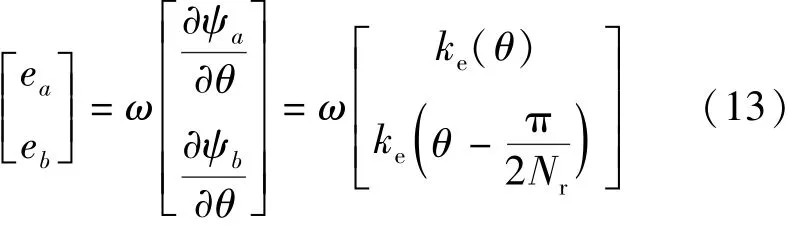
式中:ke为步进电动机旋转电压系数,该系数是转子位置角θ的函数。

另一方面,由式(4)可以得到:

式中:kt为步进电动机的转矩系数,与转子位置角θ有关。

对比式(13)和式(14)可知:

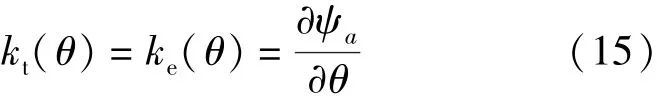
恒定转速下的空载旋转电压与对应转速的比值为空载旋转电压系数,空载时相电流为零,旋转电压等于永磁磁链产生的反电动势。该空载旋转电压系数不仅包括了旋转电压的基波分量,还包括高次谐波分量,如图4所示。

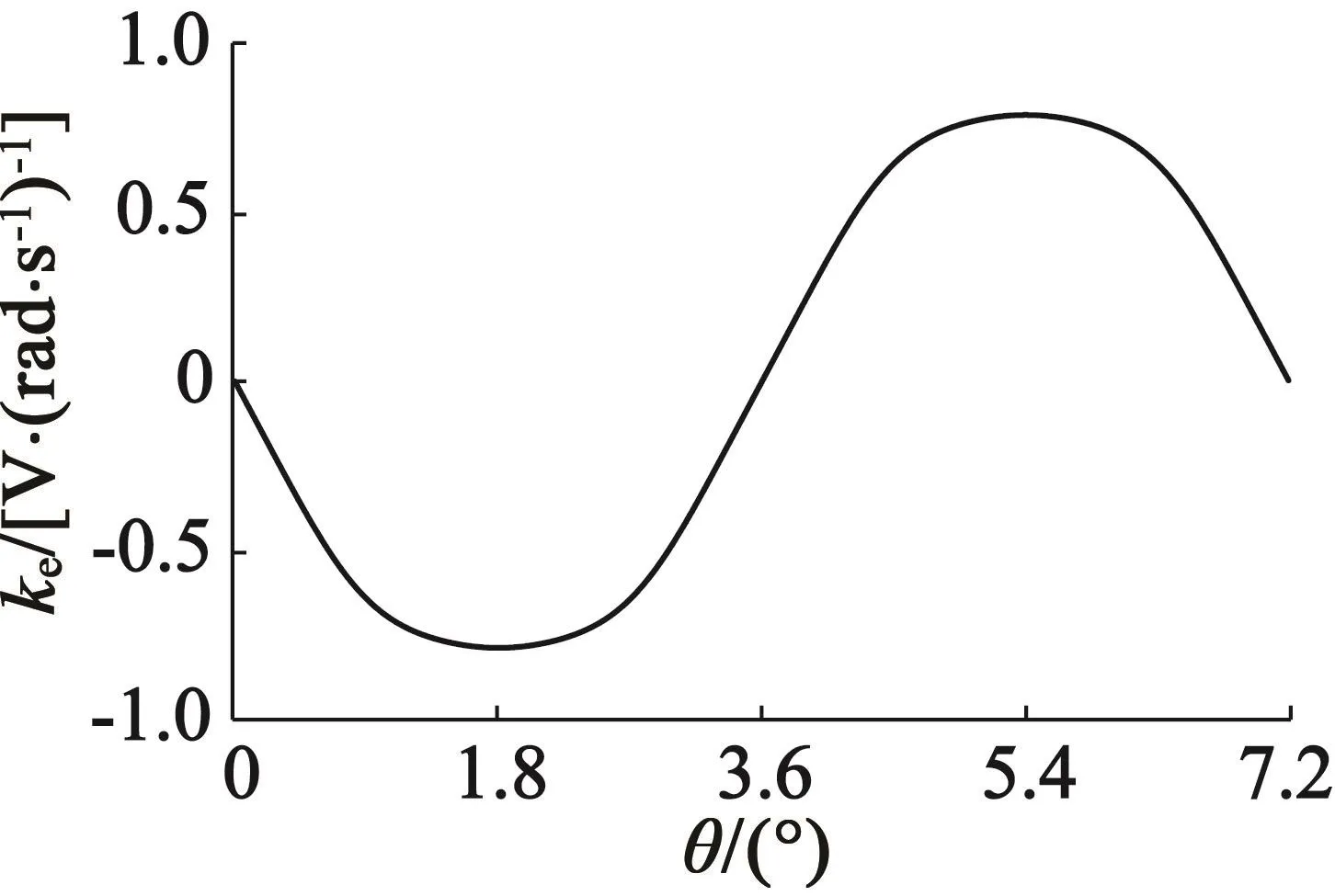
图4 旋转电压系数

1.3.2 有电枢反应的旋转电压与电磁转矩系数

空载运行时,电机绕组匝链的磁链为永磁磁链;负载运行时,电机绕组匝链的磁链还包括电枢反应磁链。负载运行时,随着电枢电流的增大,电机铁心的饱和程度增加,铁心磁导率减小,绕组磁链减小,进而导致旋转电压减小,旋转电压系数和转矩系数衰减。因此,需要分析电机铁心饱和引起的旋转电压与电磁转矩系数变化。

本模型引入衰减系数kα(ia,ib)来表示电机绕组电流对磁链的影响,负载运行时的绕组磁链可由空载磁链与衰减系数的乘积表示:

式中:Ψfa0为空载永磁磁链。因此,负载运行时的旋转电压系数:

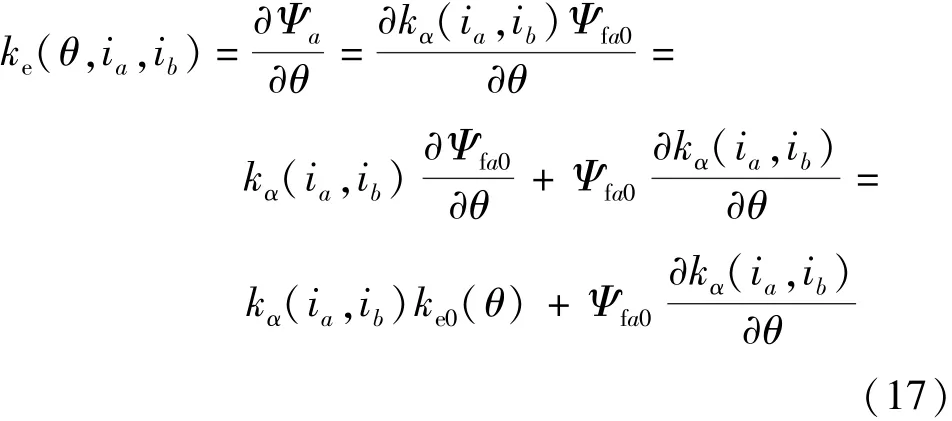
式中:ke0为空载旋转电压系数。由于衰减系数的幅值和波动较小,可以忽略衰减系数的偏导项,式(17)可进一步简化:

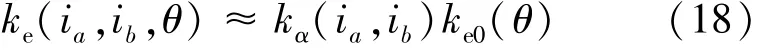
相应的,电机的转矩系数可表示:

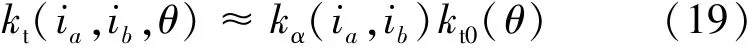
式中:kt0为空载电磁转矩系数。

由式(14)可知,当B相电流ib等于0时,如果不考虑铁心的饱和效应,电机的电磁转矩:

当考虑铁心饱和效应时,电机的电磁转矩可表示:

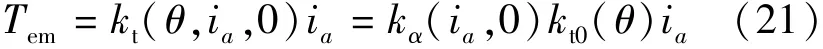
因此,衰减系数可表示:

当B相电流为0时,实验测得电磁转矩随A相电流的变化如图5中的实线所示。由于铁心的饱和效应,电磁转矩随A相电流的增大而增大,但转矩的增长率逐渐减小。

当A,B两相电流都为0时:

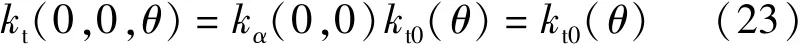
其中:

因此,图5中实测转矩-电流曲线在电流等于0附近的斜率约等于空载转矩系数。由该斜率与A相电流相乘可得不考虑饱和效应时的线性拟合转矩-电流曲线,如图5中虚线所示。由式(22)可知,在同一电流下,实际转矩与线性拟合转矩的比值即为衰减系数。

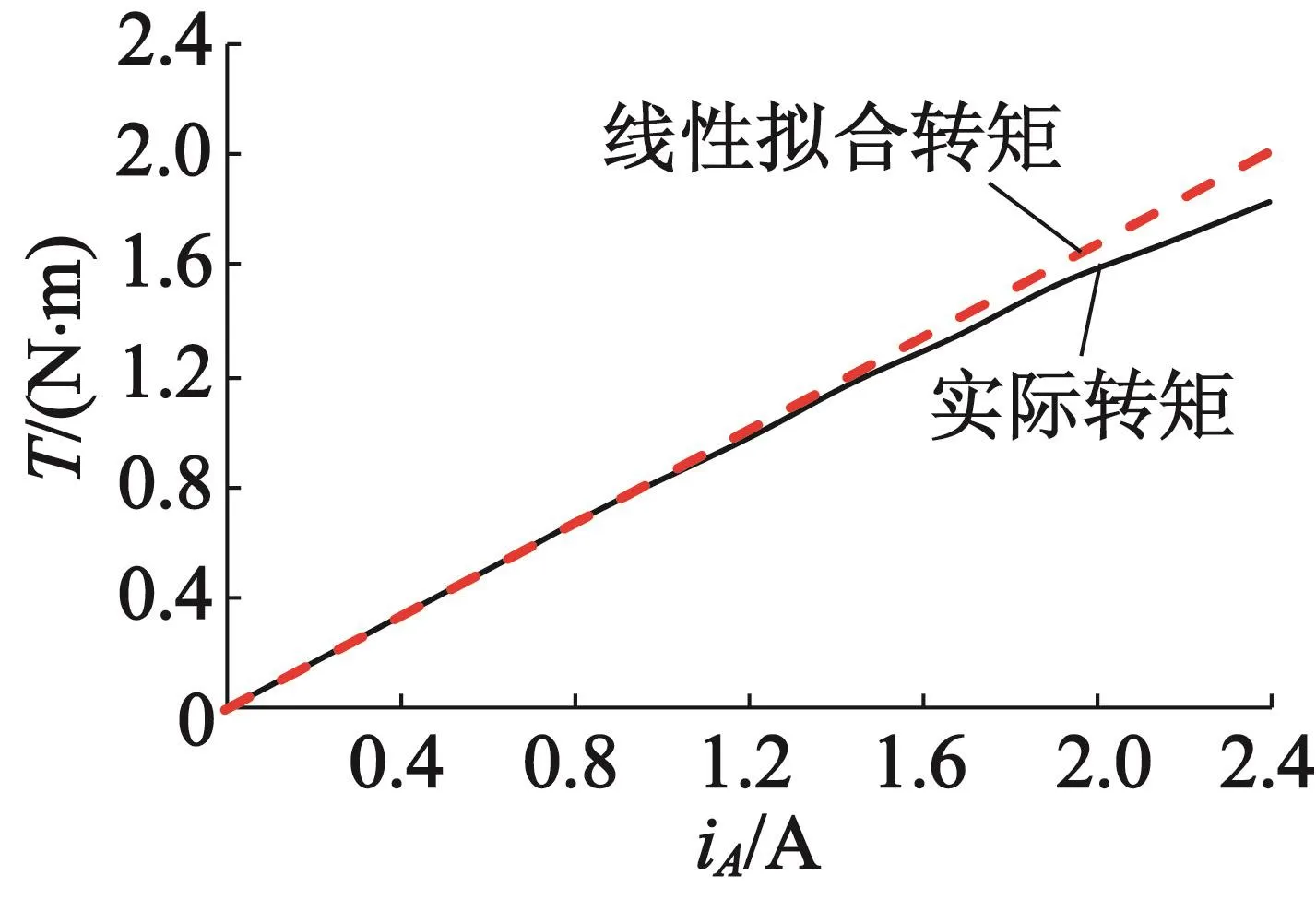
图5 铁心饱和对电磁转矩的影响

通过上述过程得到了B相电流为0时,衰减系数随A相电流的变化。改变B相电流大小,重复上述过程,即可得到衰减系数与A,B两相电流之间的关系,如图6所示。

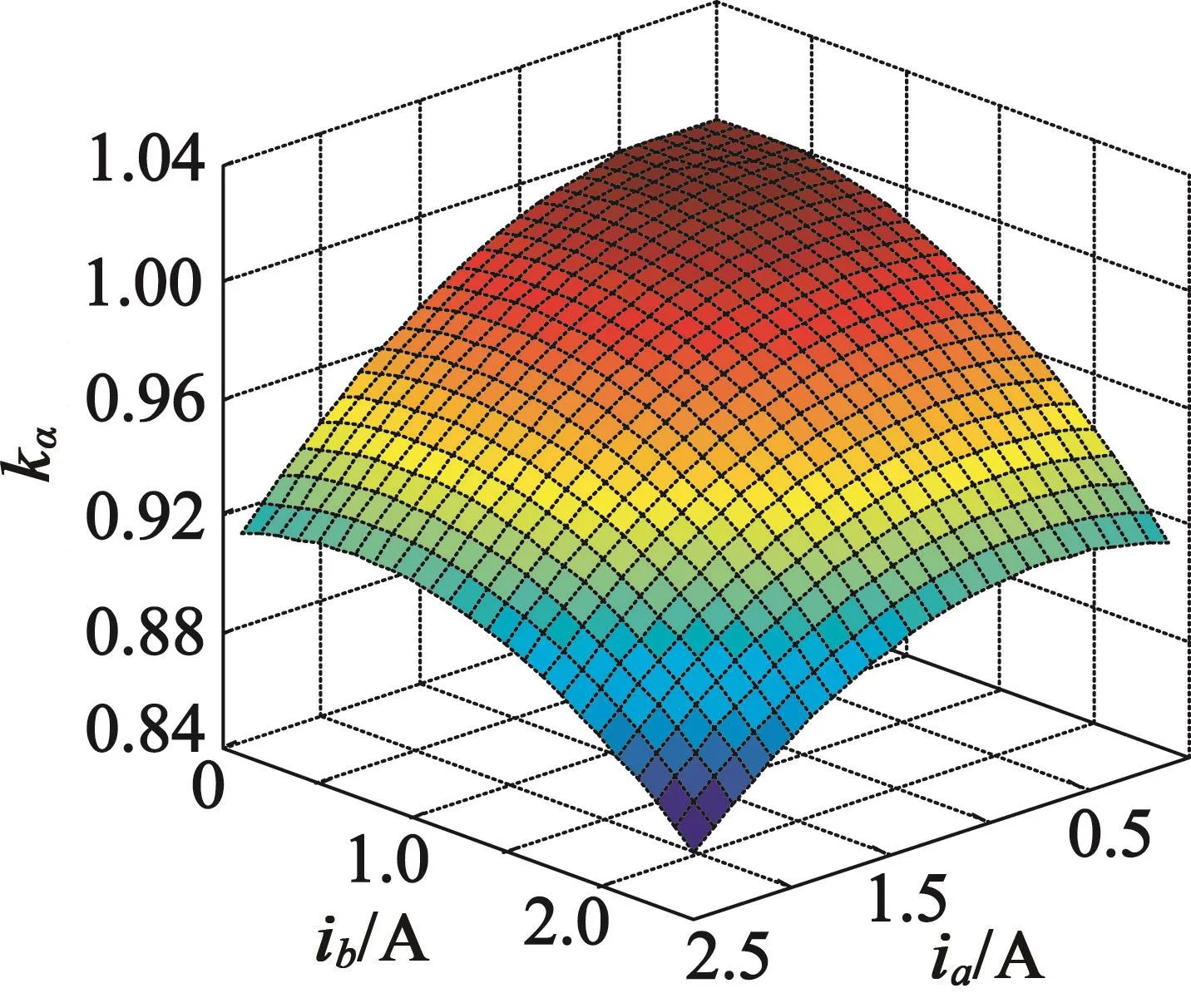
图6 电磁转矩与旋转电压衰减系数

2 驱动器精细化建模

步进电动机驱动器通常采用H桥驱动器,在本文研究的两相混合式步进电动机中,A,B两相绕组分别采用两个相同的H桥驱动器进行控制,其中驱动器与A相绕组的拓扑结构如图7所示。图7中,M为步进电动机A相绕组,U为步进电动机A相绕组端电压,T1～T4为驱动器功率管,在该步进电动机中采用MOSFET作为功率管,D1～D4为续流二极管。

本文所建立的驱动器模型为一个多状态的非线性模型,驱动器模型的输入为直流电源电压、环境温度、绕组电流和控制信号。驱动器模型的输出作为电机绕组的端电压,输入到步进电动机本体模型中,实现驱动器模型与电机本体模型的耦合。在驱动步进电动机时,H桥驱动器存在4个工作状态,分别为正向导通、反向导通、断路和短路状态,因此,需要分别建立这4个工作状态的模型,仿真时根据驱动信号选择具体的工作状态。

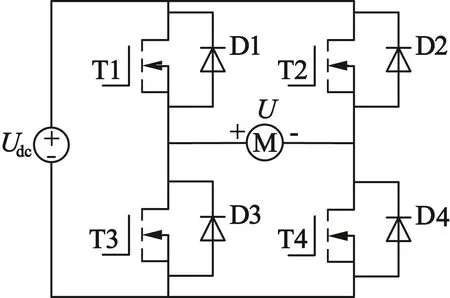
图7 A相绕组与H桥驱动器

2.1 驱动器4种工作状态

本节以图7的A相驱动器模型为例,分析驱动器模型的不同工作状态。

当功率管T1与T4导通时,步进电机A相绕组处于正向导通的工作状态,此时A相绕组的端电压U可以表示:

式中:RDS为功率管导通电阻。

当功率管T2与T3导通时,A相绕组处于反向导通状态。此时,A相绕组的端电压可以表示:

当所有功率管断开时,A相绕组处于断路状态,A相绕组端电压等于A相绕组旋转电压,驱动器的输出即为步进电动机的旋转电压。

当T1,T2或者T3,T4管导通时,A相绕组处于短路状态,此时A相绕组端电压U:

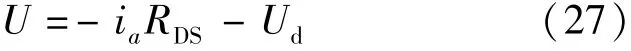
式中:Ud为二极管工作时的正向管压降。

在所建立的驱动器模型中,功率管导通电阻RDS以及二极管正向管压降Ud是影响步进电动机系统模型精度的重要参数,这些参数也会受到相电流的影响。

2.2 驱动器参数

2.2.1 功率管导通电阻

功率管导通电阻随着温度的升高呈现出非线性特性,从功率器件的数据手册中可以查到电阻在不同工作温度下的数值,但是功率管的实际工作温度受环境温度、电流大小和开关频率等多个因素的影响,需要分析不同因素对功率管实际工作温度影响,进而得到功率管的导通电阻。

在步进电动机中,电流的变化速度比较快,且步进电动机运行周期比较短,但是功率管温度的变化相对缓慢,所以功率管温度与相电流有效值有关。而步进电动机采用开环控制,功率管开关方式固定,在运行周期内的相电流平均值与控制器电流的参考值之比是恒定的,所以功率管的实际工作温度与控制器中电流的参考值有关,可表示:

式中:Tw为功率管工作温度;Ts为环境温度;ia_ref为控制器中电流参考值;k为待定系数,可由控制器给定不同的电流参考值,测量功率管的实际工作温度,得出系数k的值。

根据电流的参考值得到功率管实际工作温度,再根据数据手册获得相应工作温度时的功率管导通电阻,就可以得到电流参考值与功率管导通电阻之间的关系。

2.2.2 二极管压降

二极管正向压降Ud会受到二极管导通电流的影响。在驱动器处于短路状态时,二极管导通电流等于绕组电流,实验测得二极管正向导通压降与绕组电流的关系如图8所示。在仿真模型中,二极管的正向导通压降可根据导通电流的大小和图8曲线获得。

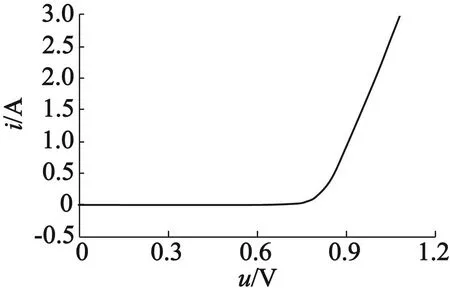
图8 二极管正向压降与导通电流关系

3 步进电动机系统参数敏感度分析

在步进电动机模型中,电机参数发生偏移对步进电动机性能的影响即为参数敏感度。同一程度的参数变化对步进电动机影响越大,则该参数敏感度越高。步进电动机电磁转矩大小与绕组电流有直接关系,以步进电动机绕组电流作为评估量,不加入控制算法,分析步进电动机中电阻、电感、旋转电压以及二极管压降的敏感度。

通过式(1)与式(25),得到步进电动机系统在正向导通状态下的A相绕组方程:

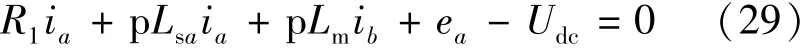
式中:R1=Rs+2RDS,R1为步进电动机系统在该状态下的回路总电阻。

同理,通过式(1)、式(26)与式(27),得到步进电动机系统反向导通状态、短路状态下的A相绕组方程分别:

式中:R2=Rs+2RDS,R3=Rs+RDS,R2和R3为步进电动机系统在该状态下的回路总电阻。

通过前面的分析可知,步进电动机系统方程中,绕组电感Lsa,旋转电压ea,二极管压降Ud均为电流ia和ib的函数,步进电动机系统正向导通状态、反向导通状态和短路状态的A相绕组方程可以分别写为式(32)～式(34)形式:

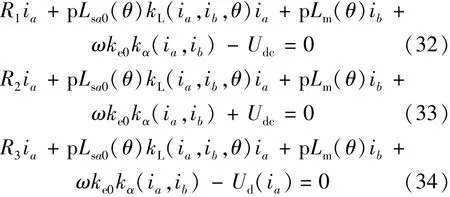
步进电动机系统是一个多状态的复杂系统,为了得到合适的评估方程,需要对步进电动机系统做一定简化。电感参数是一个随着电流与转子位置角变化的函数,由于电感参数在不同转子位置的变化值与电感平均值相比可以忽略,所以在敏感度分析时取电感平均值作为电感参数Lsa0。在正向导通和反向导通的状态下,电流关于时间的微分近似为常数。

以正向导通时的电阻参数为例,当电阻偏移后:

式中:ΔR为电阻偏移值;为电阻偏移后的A相绕组电流值。

对比式(32)与式(35),可以得到电阻参数的评估方程:

同理可得电感和旋转电压系数的评估方程:

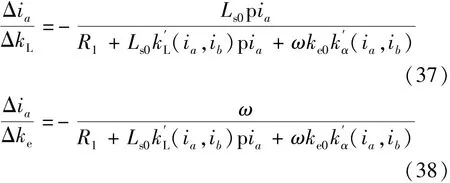
反向导通状态与正向导通状态时的评估方程相同,不予详细讨论。

A相绕组短路时,B相电流为常数,A相电流振荡衰减,幅值较小,电流对时间的微分比正向导通小。参考正向导通敏感度分析方法,可以得到电阻、电感、旋转电压系数和二极管压降的评估方程:

敏感度分析可以体现出利用衰减系数表示非线性特性的优点。采用衰减系数可以使敏感度评估方程简洁且方便表示。表1给出了该模型中各个参数的敏感度。

由表1可见,混合式步进电动机系统模型中电流对电感系数和旋转电压系数的敏感度较高,其对电流的影响较大。为了提高步进电动机系统模型的精确度,需要考虑电感系数和旋转电压系数的非线性特性。同时,驱动器参数对步进电动机系统性能也有一定影响,考虑驱动器参数可进一步提高步进电动机系统模型的精确度。

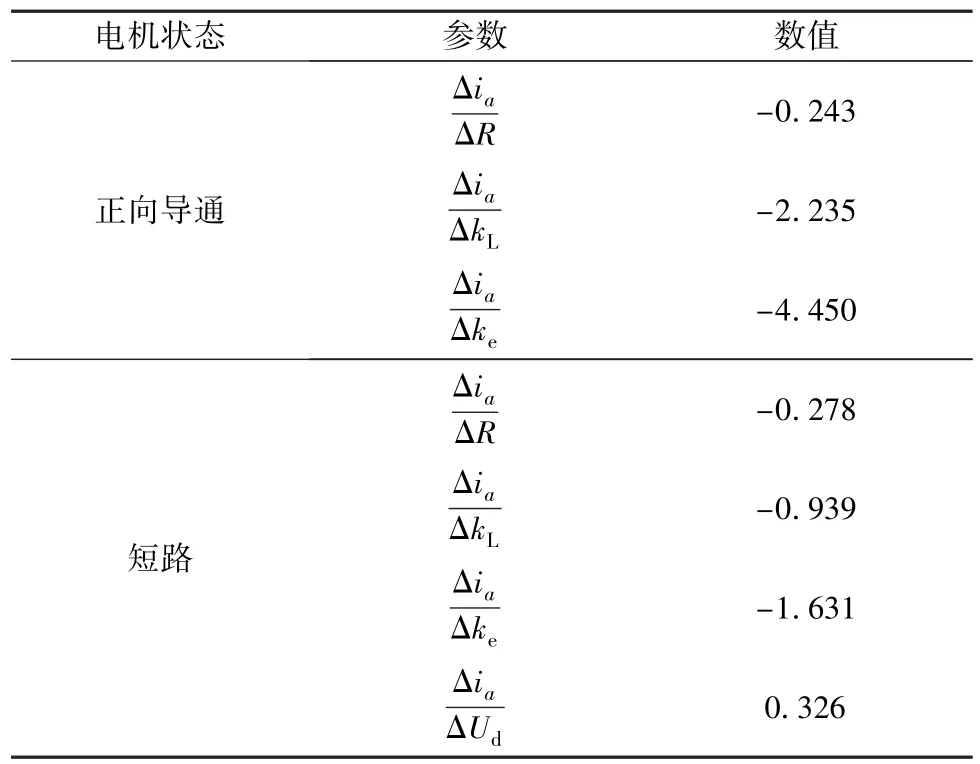
表1 参数敏感度

4 仿真实验对比

为了验证步进电动机系统精细化模型的准确性,本节将精细化模型的仿真结果与考虑理想驱动器的步进电动机系统模型仿真结果以及实验结果进行对比。其中,在考虑理想驱动器的步进电动机系统模型中,忽略了功率器件导通电阻以及二极管压降。实验采用的样机参数如表2所示。

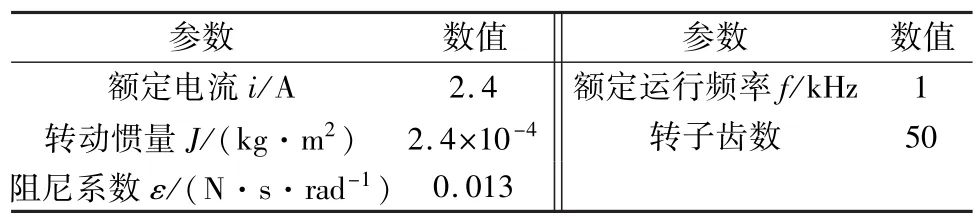
表2 步进电动机主要参数

4.1 精细化模型与理想模型对比

图9对比了精细化系统模型仿真结果、考虑理想驱动器的步进电动机系统模型仿真结果和实验结果。在考虑理想驱动器的步进电动机系统模型中,由于没有考虑驱动器中功率器件导通电阻以及二极管压降,在换相和工作模式切换时的动态响应与实验结果相比误差较大,转子位置也受其影响会出现较大的振荡。从图9中可以看出,本文建立的精细化驱动器步进电动机系统模型仿真结果与实验结果基本相同。

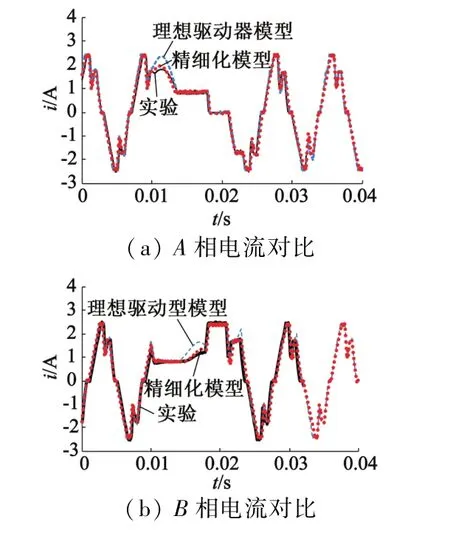
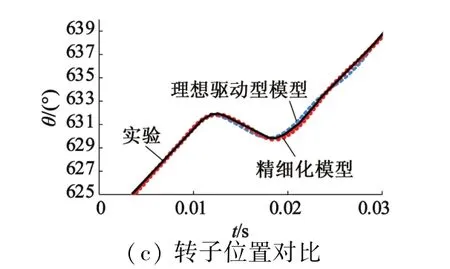
图9 精细化驱动器模型与理想驱动器模型仿真结果对比

4.2 正常工作对比

步进电动机采取降频起动,负载转矩为0.21 N·m,步进电动机在正常运行20 ms后进入保持阶段,保持8 ms后再次切入正常运行,此时步进电动机可以正常工作。实验结果与仿真结果如图10所示,可以看出,在正常运行阶段步进电动机系统精细化模型与实验结果吻合度较高。

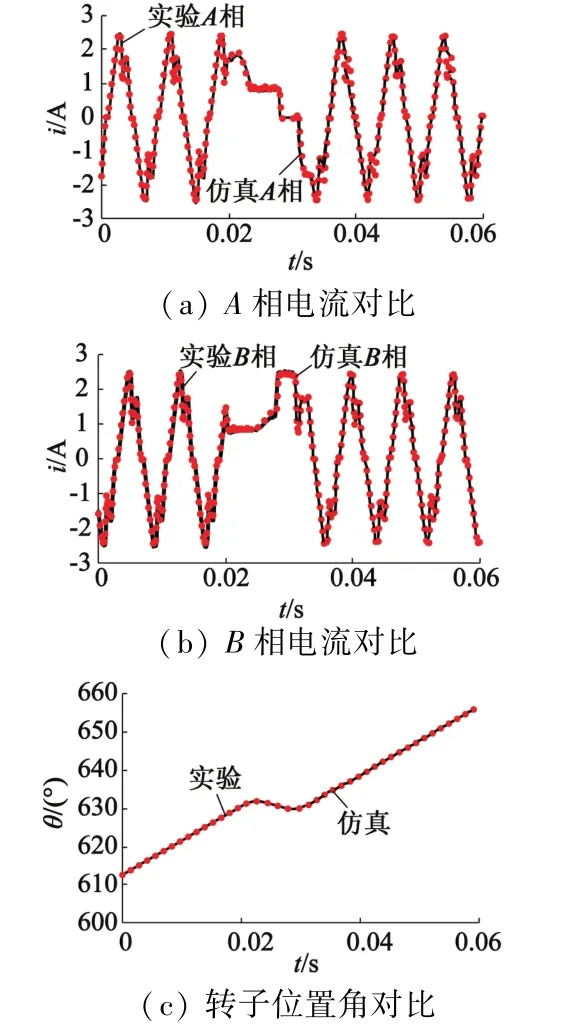
图10 正常工作电流与位置波形

4.3 单相电流保持

步进电动机单相电流保持时转子的运动过程影响电机的下次起动,特别是对于频繁起停的步进电动机,单相电流保持阶段需要重点研究。图11为该状态下的A相电流、B相电流以及转子位置角的波形对比图。可以看出在保持阶段本文建立的精细化仿真模型的电流与位置波形与实验结果吻合。

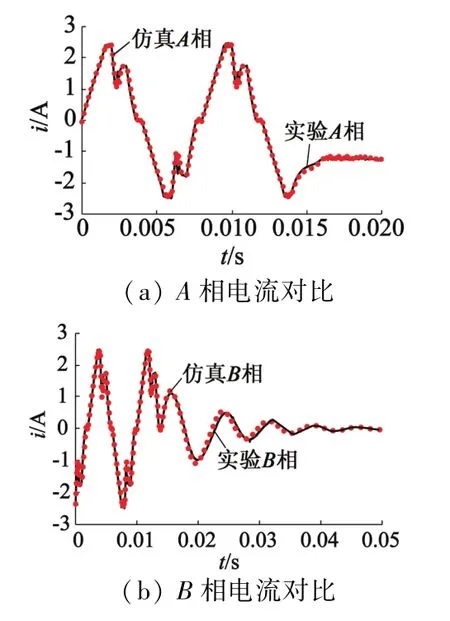
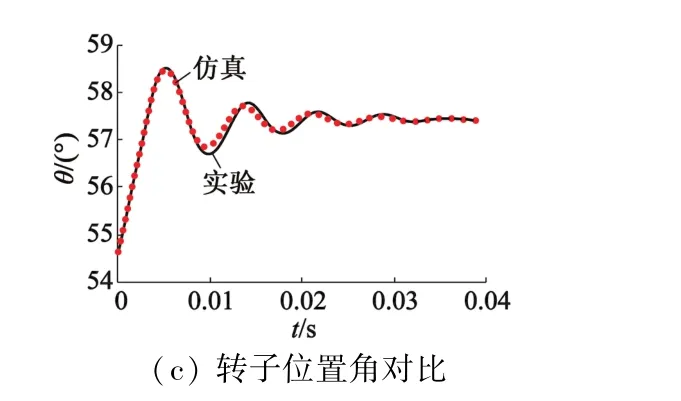
图11 单相电流保持电流与位置波形对比

5 结 语

本文建立了考虑驱动器参数的混合式步进电动机系统精细化模型。首先建立了步进电动机本体的基本数学模型,通过实验或有限元方法可以得到电机的非线性参数,在本体模型的基础上考虑了驱动器参数的影响,从传统的步进电动机本体建模扩展到步进电动机系统的建模。由仿真与实验对比结果可以看出,该模型与考虑理想驱动器的步进电动机系统模型相比,在换相和工作状态切换时的仿真精度更高,与实验结果吻合。使用该模型可以优化步进电动机的控制算法,分析失步故障等,对步进电动机性能的研究具有重要作用。