基于规则过滤和谓词覆盖的MLN迁移算法研究

吁 松， 何 慧， 王 星

(哈尔滨工业大学 计算机科学与技术学院， 哈尔滨 150001)

0 引 言

随着机器学习领域研究的不断深入，迁移学习作为机器学习领域的一个重要方向而引起研究者的高度关注与重视。 相对于传统的机器学习针对一个领域进行训练、测试和运用，迁移学习针对的是2个不同但有关联的领域，在一个领域上训练，在另一个领域上测试和运用，前者被称为源领域，后者被称为目标域。 这种训练数据与测试数据处于不同领域的要求，正是因为人们在运用传统的机器学习解决问题时，一些获取有标签数据代价昂贵或者难以收集的领域受到有标签数据不足的困扰[1]。 而这类领域正是迁移学习可以发挥作用的地方。

迁移学习从其迁移的内容来看，可以分为迁移参数、迁移实例、迁移特征和迁移关系[1]。 迁移关系的算法核心是寻找源领域和目标领域之间共享的关系，Li等人[2]就利用bootstrapping的方法迭代构建领域之间的关系。 针对马尔科夫逻辑网络[3]的迁移算法，大部分就是一种基于关系的迁移。 研究者往往是利用马尔科夫逻辑网络模型的逻辑公式作为源领域和目标领域关系的桥梁。 其中，一类算法是将MLN模型中的一阶逻辑公式转换成高阶形式，然后进行模型的迁移。 Davis等人[4]通过引入谓词变量将一阶逻辑公式转换成二阶公式，并将这些二阶公式合并成团，再对每个二阶团进行评估，将分数最高的k个二阶团迁移到目标域。 Haaren等人[5]同样是将一阶公式转换成二阶公式，但在二阶转换成一阶的过程引入了偏置，实现了效果更好的迁移。 另一类算法则是通过谓词映射的方式直接生成目标域的一阶逻辑公式，然后采用不同的策略来调整、变换公式，最终筛选公式进入MLN模型[6]，或者更简单一点，运用筛选策略不加调整地迁移公式到MLN模型中[7]。

本文设计的迁移算法是一类对目标域数据量要求不高的算法，在谓词映射算法[6]的基础上，提出了基于规则的公式迁移策略和依据权重进行谓词覆盖的迁移策略，实现了马尔科夫逻辑网络模型[8-10]的迁移。

1 MLN迁移算法

本文提出的马尔可夫逻辑网络迁移算法是一种迁移马尔可夫逻辑网络模型中一阶逻辑公式的方法。 目标领域只需要提供一个单实体为中心的实例就可以实现迁移。 迁移算法总体设计思想是将源领域的一阶逻辑公式通过谓词映射转换成目标域的一阶逻辑公式，然后利用数据验证、规则迁移和基于权重的谓词覆盖等手段迁移公式，最后生成目标域的MLN模型。 本文的最大贡献就是提出了基于规则的公式迁移策略以及基于权重的谓词覆盖策略。

1.1 数据验证

首先，MLN迁移学习算法需要通过谓词映射生成目标域公式。 本文采用局部谓词映射方法，即类型的一致性约束只针对单个公式，不同的公式的类型约束可以是不同的。 在映射过程中，研究的算法还额外要求谓词一致性，即在针对单个公式进行迁移时，源领域的谓词与目标域的谓词是一一对应的。 谓词一致性约束同样是局部的，即不同公式中的源领域谓词可以对应目标域中的不同谓词。 增加这样2种局部的一致性约束一方面可以节省算法的运行时间；另一方面相对于全局性的一致性约束而言，有利于生成多样化的迁移公式，进而提高迁移效果。

在得到目标领域的公式之后，研究利用仅有的目标域数据对这些映射公式进行验证。 在本文中，可以用数据来验证的公式即称为被数据验证的公式，简称为已验证的公式。 同时，进一步对被数据验证过的公式进行细分，将上一步得到的已验证的公式分为2种。 一种是经过数据验证成立的公式，即可行公式，另一种是数据验证后不成立的公式，即不可行公式。 研究借鉴Lilyana等人[7]的思想，提取所有可行公式中包含的映射得到可行谓词映射集合，提取所有不可行公式包含的谓词映射组成不可行谓词映射集合，利用其来筛选公式。 而且，考虑到不可行公式中的谓词映射并不都是不可行的映射，有的只是由于公式中的某个谓词的映射不好而导致公式验证失败。 因此，研究拟使用不可行谓词映射集合与可行谓词映射集合做差，得到的真正的不可行谓词映射集合。 此后用这种真正的不可行映射来筛选未被数据验证的公式，也称之为未验证公式，得到候选公式。

在前面提到过，本文算法对目标域数据量的设定是少量数据，所以不会得到太多已验证的公式，而未验证的公式数量则较多。 这些未被数据验证过的目标公式中既含有对目标域推理有价值的公式，也含有对目标域推理无价值的公式，因此就需要通过其它手段—基于规则的筛选和根据权重进行谓词覆盖—获得更多对目标域推理有用的公式。

1.2 基于规则的迁移策略

通过对已有的非迁移马尔可夫逻辑网络模型中逻辑公式的观察，研究发现大部分公式都具有如下特征：公式的前置条件参数之间的相互关联，最后推导出与之有关的结论参数的关系。 对比迁移得到的未验证的公式，有很多公式违背这个特征，存在一些相互关联的变量推导出与之无关的变量之间的关系，因此推导出一些不合理的结果。

表1是非迁移的方式得到uwcse领域的MLN模型中的2条公式。 从第一条中可以看到，前置条件是a1在a4学期教a3，a2在a4学期教a3，由此就可以得到一个可能成立的结论—a1和a2是同一人。 同理，第二条的前置条件中给出了a1出版a2，a3出版a2，a1不是学生，a3是学生，于是可以推出a1是教授的结论。 当然上述结论并不都是一定正确，只是有较大概率成立而已，但由于MLN的公式有权重来进行描述，因此可以允许这种推导出非确定性结论的公式。 表2是从imdb域向uwcse域迁移得到的MLN模型的公式中选取了2条。 第一条，前置条件描述了a2和a3的关系，但结论给出的却是a1和a2的关系，相对而言并不合理。 同样，表2中的第2条，前置条件分别描述的a1与a2的关系和a1与a3的关系，结论却给出了a4和a2的关系，也不是合理的推导。 基于上述的观察和特征的归纳，本次研究提出一个迁移候选公式的规则，筛选出的公式则称为符合规则的公式，简称为规则公式。

表2 IMDB迁移到UWCSE域得到的迁移公式

为了进一步解释基于规则的公式迁移原理，研究使用图1和图2分别解释了一个符合规则的公式验证过程和一个不符合规则的公式验证过程。 图1～2中的每个圆代表一个集合，2个圆相交的部分是2个集合共同的元素。 红色虚线圆圈表示的是作为结论的谓词的实参元素集合，箭头右边的实线圆圈代表可能被推导出关系的元素集合。 图1、图2中的2个公式的前提条件都是2个原子公式构成，这2个原子公式的实参都含有a1，因此，a1成为2个集合之间关系的桥梁，2个本没有关系的集合如今可能存在某种关系，于是并成一个集合，即箭头右边的集合。 该集合中任何元素之间都有可能存在某种可推理的关系，或者可以认定某人的身份，因此如果红色圆圈代表的集合是该集合的子集，即图1所示的情况，则相应的关系可能存在，该公式被认为是符合规则的公式，反之，如果公式中作为结论的谓词的实参不完全在前置条件实参构成的集合中，即图2所示的状态，则这个结论由条件关系推导出的可能性就低，该公式被认为是不符合规则的公式。

taughtBy(a2,a3,a4)∧taughtBy(a1,a3,a4)⟹same Course(a1,a2)

图1 符合规则的公式示意图

┐publication(a1,a2)∧publication(a1,a3)⟹adviseBy(a4,a2)

图2 不符合规则的公式示意图

需要强调的是，符合规则的公式推导出的结论也有可能是错误的，反过来，不符合规则的公式推导出的结论也是有存在可能的。 但这不会造成太多不良影响，因为马尔可夫逻辑网络是一种软化逻辑公式硬约束的模型，故而不需要模型中的公式是绝对正确的。

1.3 基于谓词覆盖的迁移策略

这里，首先要明确谓词被覆盖和谓词没被覆盖的定义。 所谓谓词覆盖是指目标域中的谓词存在于MLN模型的某个公式中，而所谓谓词没被覆盖是指目标域中存在谓词不在研究的MLN模型的公式中。 谓词覆盖就是指去覆盖那些没有被覆盖的谓词，而依据权重意味着需要优先使用权重高的公式去覆盖谓词。 研究中要尽量去覆盖所有目标域的谓词，是因为通过初步试验发现，如果某个谓词没有公式去覆盖的话，那么针对该谓词的推理就不能取得良好的效果。 因为该谓词没有公式覆盖，那么推理程序就没有推理的依据，故而得不到正确的结果。 因此，本文研发的算法考虑在经过前2步公式迁移后，在未能覆盖所有谓词的情况下，挑选剩余的公式中可以覆盖这些谓词的公式作为MLN模型公式的补充。 研究将使用alpha参数来指示每个谓词需要被多少个公式覆盖，对于不同的源领域和目标领域可以设置不同的值以达到最好的效果。 设计流程步骤是:先根据权重大小排序，然后统计目前MLN模型公式还未能覆盖的谓词或者说覆盖的公式数量还没能达到alpha参数要求的谓词，最后将公式依据权重大小补充进迁移的MLN模型中,使其尽量满足alpha参数规定的数目。

2 实验评估

在这一部分，研究将对算法进行实验评估。 这里对比了2个MLN迁移学习算法，分别是TAMAR算法[6]和SR2LR算法[7]。 这2个算法都有谓词映射的步骤，除谓词映射之外的迁移手段是不同算法之间的主要区别，因此非常适合用于与本文提出算法的对比。

为了分析算法的表现，采用了2种典型的用于分析马尔可夫逻辑网络的度量方法——AUC-PR和CLL。 研究可知，PR曲线是精确度-召回率曲线，AUC-PR是指PR曲线下的面积。 如果用一般的正确率这种方式来衡量则容易被大量不存在的关系的正确率所影响，导致评估结果与真实使用情况有差距。 条件对数似然(conditional log-likehood，CLL)则主要用于评估马尔科夫逻辑网络推理的质量，是对AUC-PR的一种补充。CLL值越大，则推理质量越高；反之，值越低，推理质量越差。 仍需看到，文中的评估方法比较简单，由此反映得出的推理质量并非精确可靠，如果模型能够生成足够有区别的阈值的话，CLL高低并不重要。

实验中使用了3个公开的关系型数据集，分别是IMDB、UWCSE和WebKB。 这3个数据集都是从现实世界中收集而来的，在时下研究的实验中得到了广泛的使用。 其中，UWCSE数据收集自华盛顿大学的计算机科学与工程系，记录了课程、教授、学生等身份信息，并记录了个体之间的关系，例如，advisedBy、taughtBy等等。 IMDB数据集是Lily Mihalkova采集自IMDB数据库的电影领域的相关信息，具体包含了导演、演员、电影等信息以及不同个体之间的关系。 WebKB数据集则记录了4所大学计算机系的Web网页和超链接信息。

实验中，测试了3个数据集构成的共6个迁移场景：IMDB→UWCSE、IMDB→WebKB、UWCSE→IMDB、UWCSE→WebKB、WebKB→IMDB、WebKB→UWCSE。 其中，箭头前方是源领域，箭头后方是目标域。 在本文的后面章节，会着重展示这4个算法在6种迁移场景中的表现，而后在这6种迁移场景中测试本文提出的迁移策略的效果，最后将基于实验讨论分析规则迁移、谓词覆盖和alpha参数在本文提出算法中的作用。

3 实验验证

3.1 实验结果对比

实验中，首先测试了4种算法在6种迁移场景下的表现，4个算法的AUC-PR值和CLL值分别见表3、表4。 表格的第一列是目标域，第二列是源领域。 RFPC是本文提出的迁移学习算法，其alpha的参数取值为4。

从表3和表4可以看出，在本文的实验中TAMAR算法和SR2LR算法表现较为相近，且TAMAR算法还略好于SR2LR算法。 2个算法在迁移的目标域为WebKB时，表现几乎一致，AUC-PR都是0.49，但是在CLL这个指标上，SR2LR又略好于TAMAR。 测试的迁移场景是UWCSE向IMDB迁移时，SR2LR表现较好，AUC-PR值比TAMAR高0.05左右。 而当迁移场景是WebKB向UWCSE迁移时，TAMAR表现较好，AUC-PR比SR2LR高0.1左右。 在其它迁移场景下，2个算法的AUC-PR的相差不大。

接下来，将2个已有的迁移学习算法与本文提出的RFPC进行比较。 从表3可以看出，在IMDB向WebKb迁移时，本文的算法比SR2LR效果要略有逊色，但在剩余的全部数据上，本文的算法在AUC-PR这个指标上是超过SR2LR算法的，因此在整体上来看，本文的迁移算法得到的马尔可夫逻辑网络模型能够做出更好的推理。 从表4可以看到，本文的迁移算法在CLL指标上普遍比SR2LR算法差，除了UWCSE向IMDB迁移时，本文的算法的CLL指标比SR2LR高之外，这意味着本文算法的推理结果概率普遍低于SR2LR算法。 这可能是因为本文的算法未能进行权值的调整。 但是如前述分析可知，如果推理概率的阈值选择恰当，就不会影响本文算法的预测效果，因此这也不会意味着本文的算法比SR2LR算法更差。 在与TAMAR算法比较时，本文的算法在迁移目标域为UWCSE时，AUC-PR的值比其略有不及，但在其它迁移场景中，本文的算法均是优于TAMAR的，并且在UWCSE向WebKB和WebKB向IMDB迁移时，本文的算法在AUC-PR指标上将远远高于TAMAR。 因此，从整体上来看，本文的算法比SR2LR和TAMAR都是要好的。

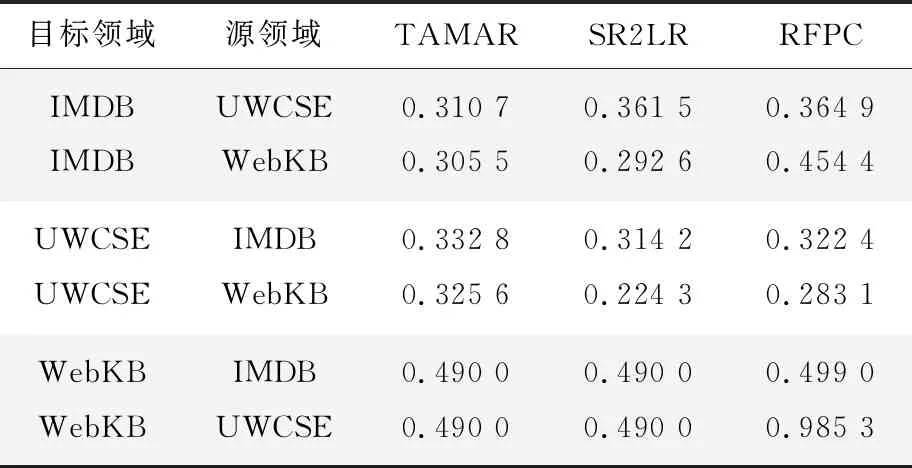
表3 不同算法在不同数据集上的平均AUC-PR的值

表4 不同算法在不同数据集上的平均CLL的值

3.2 实验结果分析

基于前述仿真测试研究过程，这里拟将探讨剖析RFPC算法中不同部分发挥的作用。 同样，研究在6种迁移场景下对比这些算法的效果，运行后详情见表5、表6。 其中，Only-Data代表只使用被目标域数据验证过的公式生成MLN模型，Data+Rule代表了用数据验证过的公式和规则迁移公式构成的MLN模型。 最后一列代表了完整的RFPC算法(alpha参数的取值为4)，该算法迁移得到的MLN模型中包含了数据验证的公式，规则迁移的公式和依据权重进行谓词补充的公式。

从表5中可以看到，除了向UWCSE领域的迁移之外，Data+Rule的方案都比只有Data的方案要好，而且大部分情况下均是如此。 例如，Data+Rule在WebKB领域向IMDB领域迁移时，AUC-PR值比Only-Data高出了0.157 4。 更为明显的是当源领域为UWCSE、目标域为WebKB的情况，Data+Rule的AUC-PR值接近Only-Data的AUC-PR值的2倍。 即便是在向UWCSE迁移时，Data+Rule只比Only-Data在AUC-PR值上低了一点点。 从IMDB向WebKB迁移的时候，Only-Data和Data+Rule则显出劣势，AUC-PR为0是因为数据验证和规则迁移两种策略都不能得到合适的公式，此时MLN不会在这种情况下进行推理，故而对应的AUC-PR值为0。 此种情况下，根据权重进行谓词覆盖的作用就得以体现，在补充了一些权重较高的公式之后，RFPC算法依旧能够取得较好的效果。 在前2种公式迁移策略能够有效发挥作用时，根据权重进行谓词覆盖的效果将不再直观明显，但如果alpha设置合理，那么对推理效果也能有一些提升，关于该点将在下文予以阐释分析。

表5 不同算法在不同场景下的平均AUC-PR的值

表6 不同算法在不同场景下的平均CLL的值

由于研究的算法中有一个alpha参数，指示了研究在覆盖谓词时需要选择多少公式，所以研究有必要对其进行深入分析，探寻考察不同的alpha参数会对算法效果产生的影响。 同样测试了在6种迁移场景下，alpha参数对RB算法的影响，alpha参数设置的范围为[0,18]。

从图3中可以看到，除了之前分析过的情况，alpha参数对算法效果的影响较为有限。 在alpha参数增加时，在一定程度上将会提升算法的效果，但有时也会导致算法效果下降。 研究中可以在IMDB向UWCSE和WebKB向UWCSE迁移时发现较大的波动，说明在Data+Rule的AUC-PR值不高时，alpha参数影响相对较大。 当Data+Rule的AUC-PR值较大时，alpha参数的影响相对较小，正如研究中看到当UWCSE向WebKB迁移时未见任何波动。 由此也可以推断得出，作为本算法的关键部分—基于规则的公式迁移策略—起着关键的作用，用于覆盖谓词的公式起到一个补充的作用，而alpha参数却只是用于最后的微调。

图3 alpha参数对算法的影响

研究至此，又统计了RFPC算法(alpha参数设置为4)在所有迁移场景下生成的MLN模型中不同来源的公式数量。 并且推导计算了每类公式为推理效果做出的贡献，用于详尽评估每种迁移策略的效果。 计算公式贡献的方法为每类公式带来的AUC-PR的提升除以该类公式的数量。

图4展示的是alpha参数设置为4时，RFPC迁移算法生成的模型中不同来源的公式的分布情况。 从图4中可以看出，不同的迁移场景，不同来源的公式分布情况是不同的。 除了2种极端情况，也就是IMDB向UWCSE迁移时数据验证的公式占主导和IMDB向WebKB迁移时只有谓词覆盖的公式以外，研究发现基于规则的迁移公式构成了MLN迁移模型公式的主要部分。

图4 不同迁移策略得到的公式的平均数量

图5展示的是不同类别的公式为最终的推理效果做出的贡献。 由图5可以看到，除了IMDB向WebKB迁移的时候(因为该迁移场景下MLN模型中只有谓词覆盖的公式)，数据验证迁移的公式做出了最大的贡献。 正如研究所希望的，基于规则的公式贡献总体而言仅居次席，并且相对来说是明显大于基于谓词覆盖的公式，这说明本文提出的规则发挥了应有效果，规则迁移的公式要远远胜过根据权重进行谓词覆盖得到的迁移公式。 某些情况下，基于规则的公式贡献比基于数据验证的公式贡献明显要小，这是因为真实的数据是检验映射公式的最佳规则。 需要特别注意的是，基于数据验证的公式中也会存在部分公式符合规则，这也说明满足规则的公式所做出的实际贡献会高于图5中所显示的贡献。

图5 不同迁移策略得到的公式的平均贡献

4 结束语

本文研究提出了一种针对极为有限的目标域数据的MLN迁移算法，通过提出一种符合逻辑的公式迁移规则，在没有目标域数据支撑的情况下迁移映射出来的目标域公式，并根据迁移公式的权重，尽量覆盖所有目标域谓词。 通过在6种迁移场景下的实验验证，可以看到本文的算法超过现有的MLN迁移算法，同时也验证了本文提出的规则的有效性，以及基于权重覆盖目标域谓词的价值。

在后续的工作中，研究将尝试把MLN迁移学习算法运用到更多领域中去，考虑在多个源领域向一个目标域迁移的场景中运用本文的算法以及提出更多迁移公式的规则或算法使得在没有更多目标域数据支撑的情况下迁移更好的公式到目标域。