双曲型界面问题的变网格低阶有限元方法

关宏波,洪亚鹏,曲双红

( 郑州轻工业大学数学与信息科学学院,河南 郑州450002)

1.引言

界面问题在材料科学、流体力学和电磁场问题等工程领域有着重要应用,例如带有不同传导系数的热传导问题、具有不同粘性系数的两相流问题以及电磁场中存在绝缘分界体等具有两种或两种以上介质的情形[1].此类问题的精确解通常不易解析表达,于是研究其数值方法就变得十分有意义.而有限元方法在众多数值计算方法中具有举足轻重的地位,界面问题的有限元方法根据网格剖分形式大体可以分为两类：拟合有限元方法和非拟合有限元方法.其中非拟合有限元方法是指网格剖分与界面所处位置无关,如具有代表性的浸入有限元方法[2],其主要技巧是修改界面单元上的基函数使其满足界面条件,得到界面单元内部的分片多项式空间,新的求解空间对界面问题的解有较好的逼近效果[3−5].但是该方法也有不足之处,比如即使原问题满足相应的连续性和强制椭圆性,得到的数值解却也是非对称的,界面单元所对应的刚度矩阵与非界面单元刚度矩阵差异较大.而拟合有限元方法是指在网格剖分时要考虑界面所处位置进行适当剖分,文[6]最早引入了对求解区域沿界面进行特殊剖分,使界面作为单元边界或单元顶点,此类方法的优势在于最终合成的总刚矩阵与传统偏微分方程结果一样,均为对称正定的,这给数值计算带来诸多便利之处.基于此,文[7]提出了一种无限元方法,用无限剖分的思想与有限元方法的结合,得到了能量模意义下的最优误差估计结果,但是该方法对于曲边型界面问题是不适用的.文[8]克服以上缺陷,得到了有限元方法的最优误差估计结果,但是其对精确解的正则性假设过高,不但要求精确解及其外法向导数沿界面方向连续,而且要求解在每个子区域里具有四阶偏导数,这一限制过于苛刻.陈志明院士和邹军教授在文[9]中提出了一个简单的P1协调三角形有限元方法,在L2模和能量模意义下得到了次优的误差估计结果,并且在文中的一个注解里给出了能够达到最优误差估计的一个正则性假设条件.邹军教授等人[10]在对此类问题解的正则性进行更为精细探讨的基础上,通过引入一个拟插值算子,得到了一般k阶有限元逼近下的最优阶误差估计结果.本文作者之一将其推广到了非协调有限元逼近格式[11],同样导出了最优阶误差估计.两个印度学者Sinha和Deka对文[9]中关于假设正则性得到更高收敛阶的注解进行了重新论证,得到了最优阶L2模和能量模误差估计,并应用于抛物型界面问题的半离散和全离散Galerkin格式[12−13].然而在许多实际问题中,界面的位置和形状都有可能会随着时间的不同而产生相应的变化,于是在不同时间节点处允许采用合适的网格剖分具有一定的应用价值.梁国平院士在文[14]中针对抛物问题提出了一种变网格有限元处理方法,其基本做法是:对空间域采用有限元方法,对时间轴采用差分法,并且对于不同时间的空间区域可以采用不同的网格.后续有不少国内外学者将该方法应用到更多的非定常偏微分方程问题中,其中包括协调和非协调有限元方法[15−18].然而对于界面问题的变网格方法,目前尚未见到有文献正式出版.本文将采用变网格技术,将拟合有限元方法应用到双曲型界面问题中,采用最低阶的P1三角形协调有限元对空间变量进行逼近,得到相对于网格剖分尺寸和时间离散步长的最优误差估计结果,并将该方法进行推广应用于其他情形,从而拓宽了有限元的应用范围.

2.双曲型界面问题

考虑如下双曲型界面问题:求u ∈L2([0,T];X(Ω)),使得

其中Ω ⊂R2为一个凸多边形区域,Ω−为Ω内部的一个开区域,其边界Γ=∂Ω−也包含于Ω内,并且具有C2光滑性,Ω+=Ω−Ω−,如下图2.1所示.定义X(Ω)=H10(Ω)∩H2(Ω+)∩H2(Ω−),本文中所用到的Sobolev空间及模均为标准记法(见文[19]).

图2.1 Ω=Ω−∪Ω+

问题(2.1)在界面处满足如下跳跃性条件:

其中[u]Γ为u跨过界面Γ的跳度,n为相应于界面Γ的单元外法向量,而

这里s=+或−.

令Q=,(2.1)式等价于下面形式:

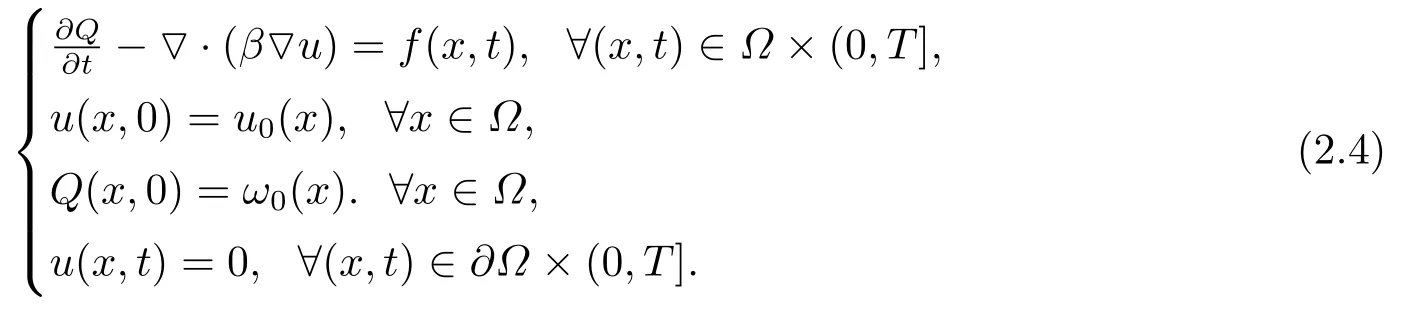
(2.4)式所对应的变分形式为：求u(x,t)∈(0,T]→H10(Ω),使得

其中

下面对区域Ω进行拟一致三角剖分Th.首先用一个凸多边形Ω−h逼近Ω−,Ω−h的顶点都位于Γ上,Ω+h=Ω−Ω−h.然后对Ω−h和Ω+h分别进行拟一致三角剖分,但是其中的三角形单元K要满足以下两个条件：

1)K要么在Ω−h内,要么在Ω+h内;

2)假设F为K的一条边,如果F ∩Γ≠Ø,则F的两个顶点在Γ上或者整条边都在Γ上.

如果K与Γ没有交点,称此类单元为非界面单元; 否则K为一个界面单元,记界面单元的全体为Th∗,而hK为单元K的直径,对于任意的界面单元K,记K−=K ∩Ω−,K+=K ∩Ω+.由于Γ是C2光滑的,则meas(K−)≤ch3K与meas(K+)≤ch3K中必然有一个是成立的,其中meas(·)为测度,这里及以后出现的c均为一个与网格剖分尺寸及时间离散步长无关的正常数.为方便起见,我们记K为Ks中满足meas(Ks)≤ch3K的那一个.

在Th上定义线性协调P1三角形有限元空间Vh,并记Πh:H10(Ω)→Vh为相应的插值算子,由文[9]知,如果进一步假设Ω0为包含界面的某小一邻域,当h足够小时,必然有T∗h ⊂Ω0,满足u ∈W1,∞(Ω−∩Ω0)∩W1,∞(Ω+∩Ω0),能够得到如下最优阶的插值误差估计:

(2.5)式的有限元离散形式为:求uh,Qh ∈Vh满足

3.变网格方法及误差估计

首先引入变网格的主要思想,设0=t0< t1< t2< ··· < tN=T将时间轴平均分成N段,分点为tn,n=0,1,2,··· ,N,∆t=tn+1−tn=令Thn为tn时刻对空间区域Ω的一个三角形剖分簇,V nh为tn时刻的有限元空间:V nh= {v(x,tn);v ∈Vh}.

我们选取uh(x,t)的近似解空间Sh如下:Sh上的函数uh(x,t),有N+1个有限元插值函数,即uh(x,t)在N+1个节点的节点值,在时间间隔tn < t < tn+1内,uh(x,t)取为t的线性函数,通过线性连结相邻两个节点uh(x,tn)和uh(x,tn+1)而得到.近似解uh(x,t)在各个时间点处的函数值unh=uh(x,tn)由以下格式确定:

变网格有限元解与精确解的误差主要包含以下三个部分:对时间变量的差分误差、对空间变量的有限元误差以及网格变动误差.下面的引理3.1首先给出差分误差的估计.

引理3.1记un=u(x,tn),Qn=Q(x,tn),则成立

证注意到Vh ⊂H10(Ω)为协调有限元空间,在(2.5)中令v=vh,并从tn到tn+1积分,得

然后(3.2)与(3.4)相减,可得

利用差分性质及Cauchy不等式,上式右端两项可分别估计为:

和

引理得证.

为书写方便,我们引入以下记号:

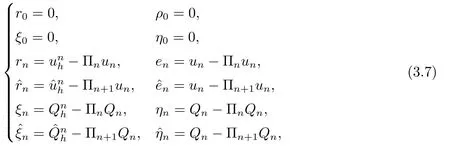
其中Πnun为tn时刻un的有限元插值,n=1,2,··· ,N−1.

引理3.2假设时间剖分参数0<∆t < d <1(其中d为一正常数),对于n=1,2,··· ,N−1有

其中

证(3.1)中第五个式子与(3.2)相减,有

由(3.7)得

从而结(3.10),有

在上式中取vh=ξn+1+,则

由(3.1)中最后一个式子得到

将上式代入(3.12)式得

其中β∗=min(β+,β−).

我们对上式右端五项利用Cauchy不等式,拟不等式及引理3.1,分别估计为:

和

将(3.14)-(3.18)结果代入(3.13)式中,有

由(3.1)式中第一个式子,显然(∇(−rn),∇vh)=(∇(−en),∇vh),∀vh ∈V hn+1.在上式中取vh=,则||1≤|rn|1+|−en|1,对上式两端平方,并由Cauchy不等式可得

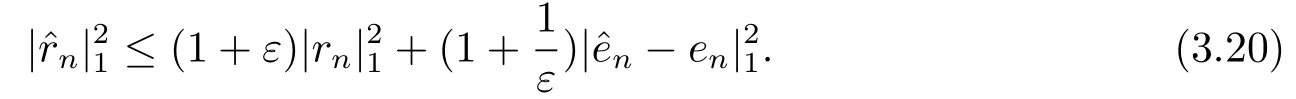
同样利用上述技巧,由(3.1)式中第二个式子可得到

将(3.20)和(3.21)式代入(3.19)式,有

而当两层网格之间不发生变动时,为

假设计算过程中共有M次网格变动,不妨设前M层网格变动,后N−M层网格不变动,将各层对应的估计式写出,并适当使用技巧对其求和,可得

下面给出本文主要结论:

定理3.1假设unh,Qnh ∈V nh和un,Qn ∈X(Ω)分别为(2.5)和(2.7)的解,则

证因为

所以由引理3.2得

引理得证.

注3.1由估计式可以看出,网格的变动次数不能是任意的,只有当M为一个与h及∆t无关的有界数时,误差的估计阶才是最优的.

4.推广应用

本文主要针对双曲型界面问题提出了一个变网格的有限元方法,在理论分析及推广应用过程中,需要指出以下三点:

1)在误差估计过程中,我们用到了该P1有限元空间的关键性质,即对于任意的vh ∈Vh,(∇vh)|K为常数.于是该方法对于非协调的P1三角形元[11]和CNQrot1矩形元[20]也是适用的,但对于其它一些常见的协调和非协调元,该理论还不能直接应用.

2)该方法可以通过适当调整逼近格式,推广应用于其它的一些界面问题,如半线性界面问题、线弹性界面问题等.

3)当定义区域Ω为一个窄边型区域时,可以抛弃拟一致剖分限制,考虑采用各向异性剖分[21],从而达到减少总体自由度的效果.

总之,该变网格方法为处理界面问题提供了一种新的思路,对设计时间相关界面问题的自适应算法是有益的.