多分段坐底式船型结构物对地载荷研究
孙雪荣
(中国船舶及海洋工程研究设计院,上海 200011)
坐底式船型结构物为直接坐底于海底区域或海底的特殊海洋工程结构,目前对普通坐底式海洋结构物的研究已较为成熟,而对沿船长方向有不连续坐底区域的坐底式海洋结构物的研究缺乏具体的实际工程经验和设计方法。
目前总体配载设计经验仅针对普通坐底和自由飘浮状态的海洋工程,沿船长方向多分段的坐底式船型结构物设计的经验目前无工程可借鉴,其困难在于总体配载的困难,以及目标作业海域的海沟纵横导致的不同船底坐底工况,且目标作业海域远海深水波到达海底浅水区域后,破波、爬升等现象导致目标结构物外载荷不同于常规浮式海洋结构物和常规防波堤式海岸工程[1-2]。
本研究并未对多分段坐底式船型结构物本身的坐底稳性、结构设计等进行相关阐述,而是着重于多分段对地载荷的求解,因本改造工程坐底工况较为复杂多变,各坐底工况之间对船体配载的要求并不一致,而对地载荷的求解尤其事关整项工程的设计安全和设计进展,因而正确合理且快速可行的确定多分段坐底式船型结构物对地载荷求解方式是本工程的首要核心任务。
以下以本改造工程为例,从对地载荷函数求解、静水载荷下对地载荷求解、波浪载荷下对地载荷求解、船体装载优化角度上全面阐述沿船长多分段坐底式船型结构物的对地载荷,为后续本工程的总体及结构设计提供设计输入基础。
1 对地载荷函数求解
多分段坐底式船型结构物的对地载荷求解以泥面仅承担垂向对地压力[3-4]为首要计算前提,结合船型结构物的垂向载荷平衡及相应力矩平衡为刚体力学[5-8]理论基础,力学理论基础公式如下:
分段连续的坐底反力函数(坐底示意图见图1):
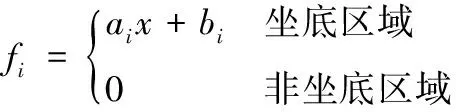
式中,i=1,2,…,n,n≥1;ai、bi为每次迭代所求解的因子。
船型结构物垂向载荷静平衡方程:
船型结构物垂向载荷沿船长方向引起的力矩静平衡方程:
式中:WD(x)为船体质量沿船长分布的离散函数;FD(x)为船体浮力沿船长分布的离散函数;fi(x)为沿船长分布的对地反力分段函数;L为船长。
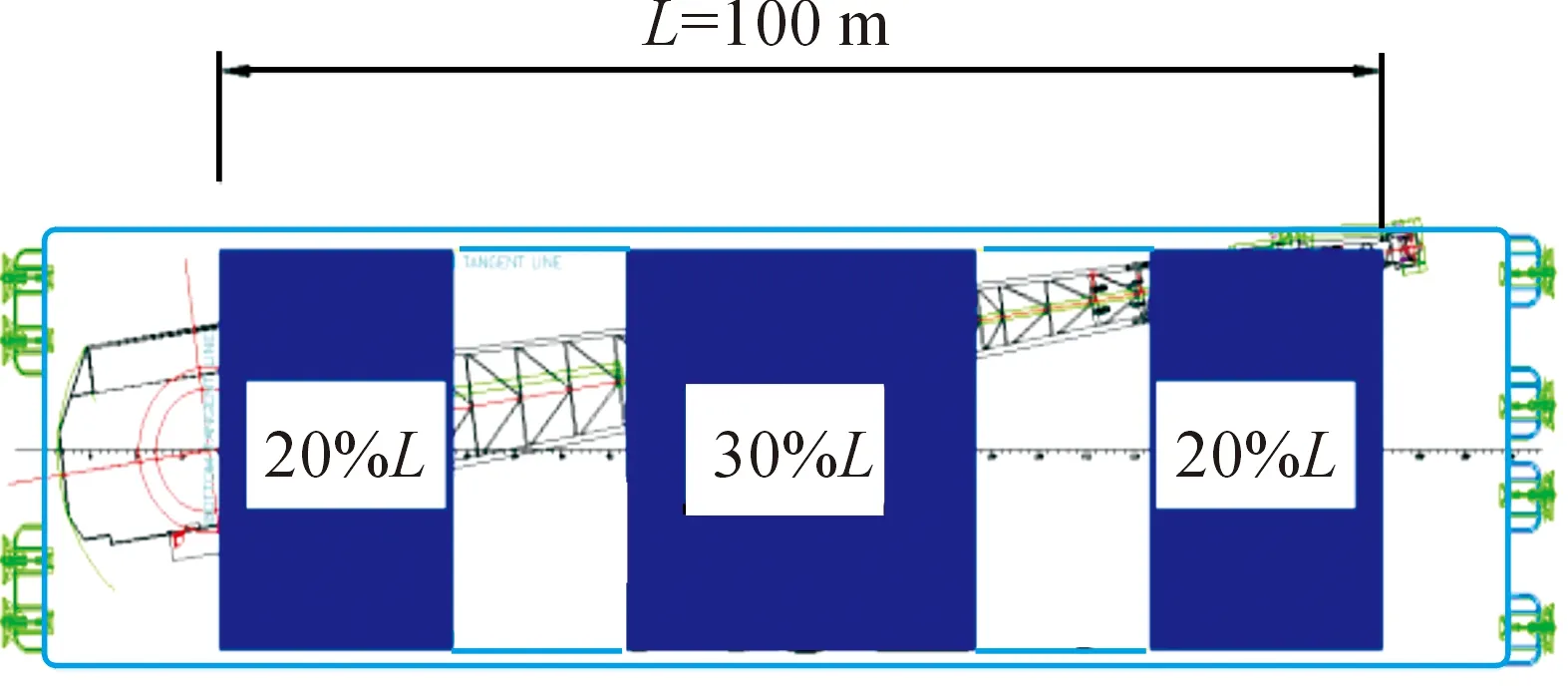
图1 多分段坐底式船型结构物坐底示意图(阴影区为坐底区域)
1.1 初始坐底载荷函数求解
单分段坐底载荷函数虚拟进行初始输入值求解,为以后的多次数值迭代做准备。
单分段虚拟坐底载荷函数,沿船长分布的范围涵盖目标工程的所有坐底区域:
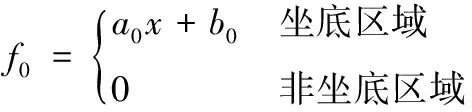
垂向静载荷平衡方程:
垂向静载荷沿船长积分矩平衡:
求解得到a0、b0
1.2 坐底载荷函数迭代求解
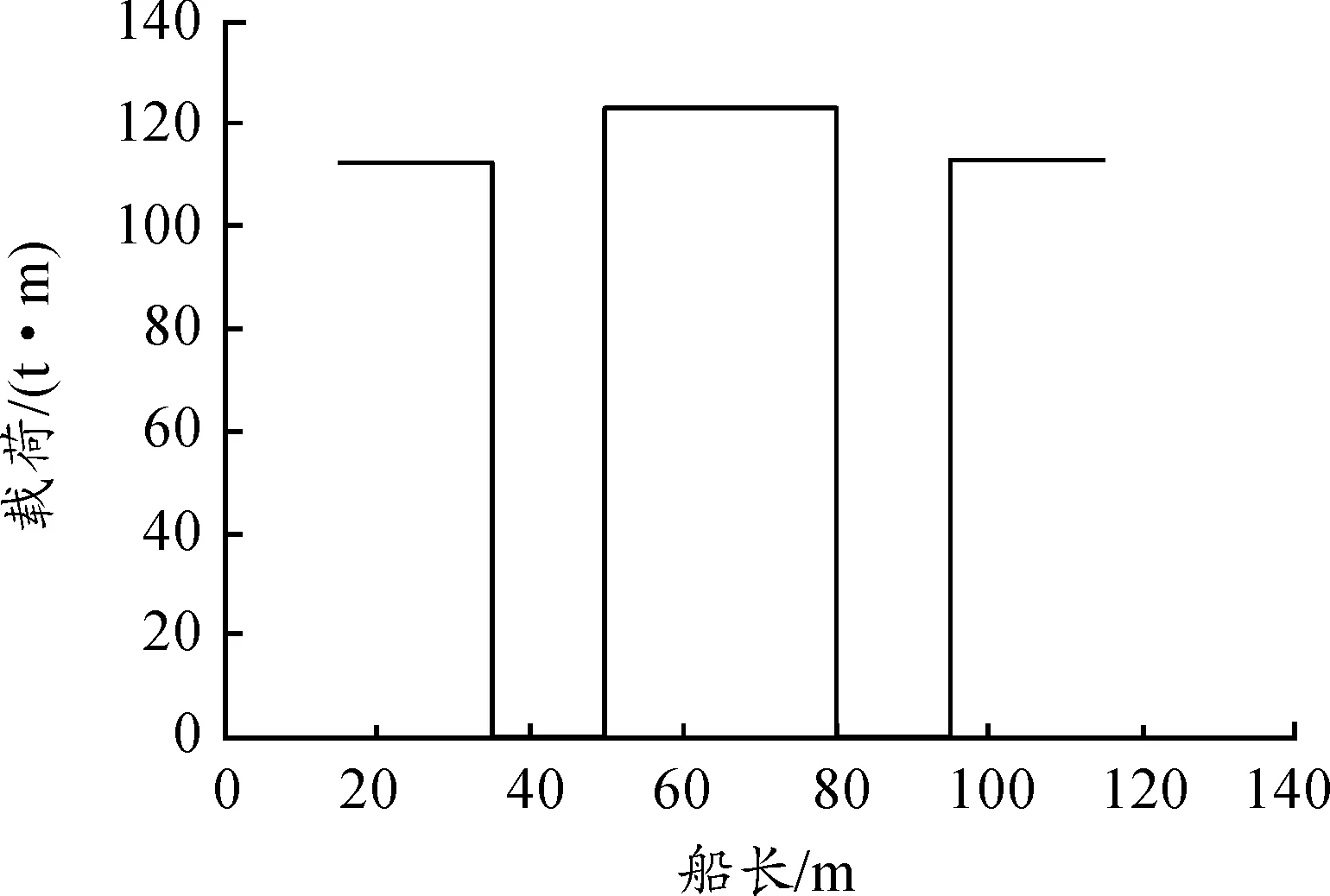
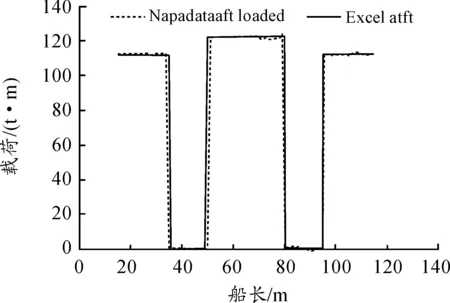
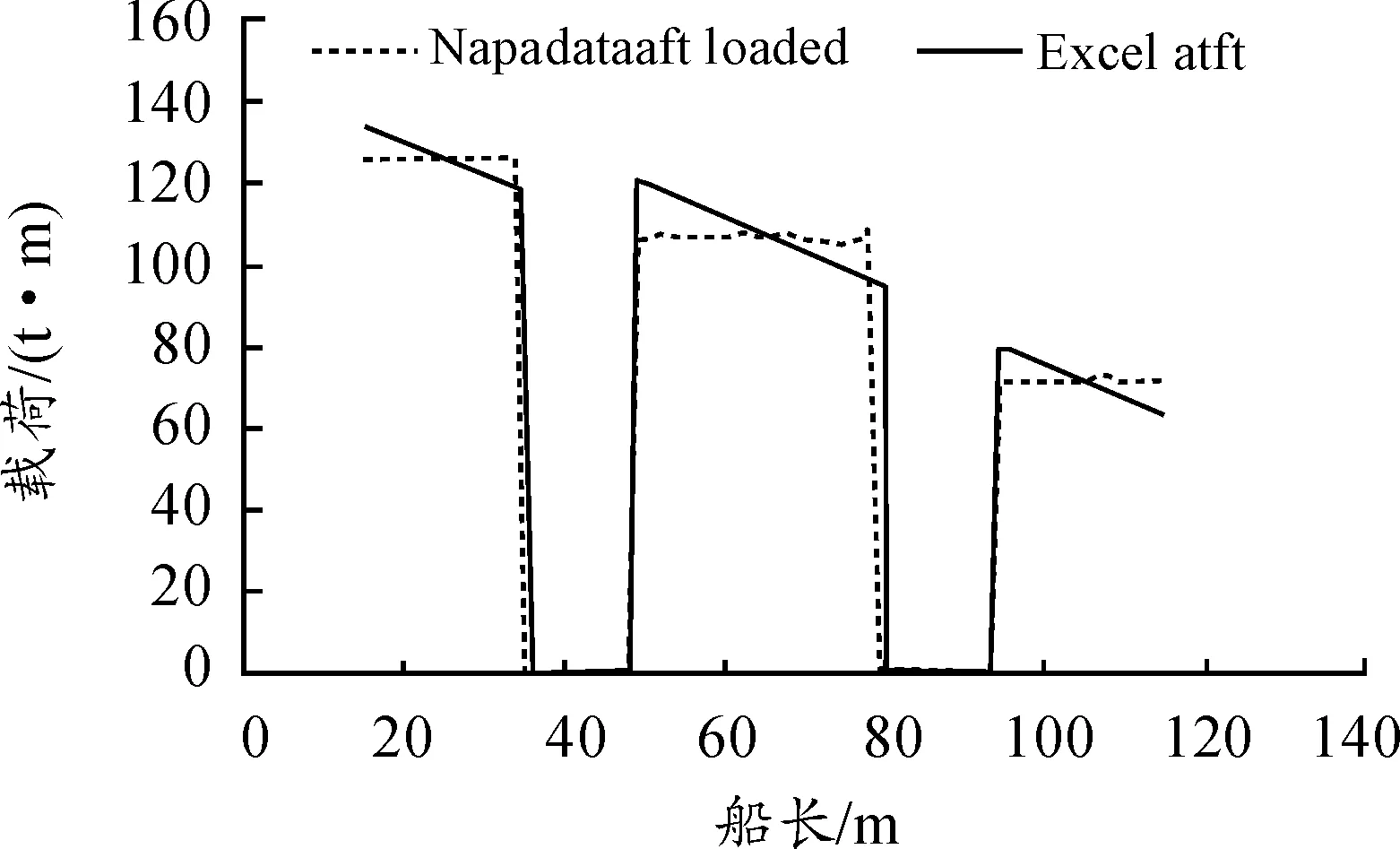
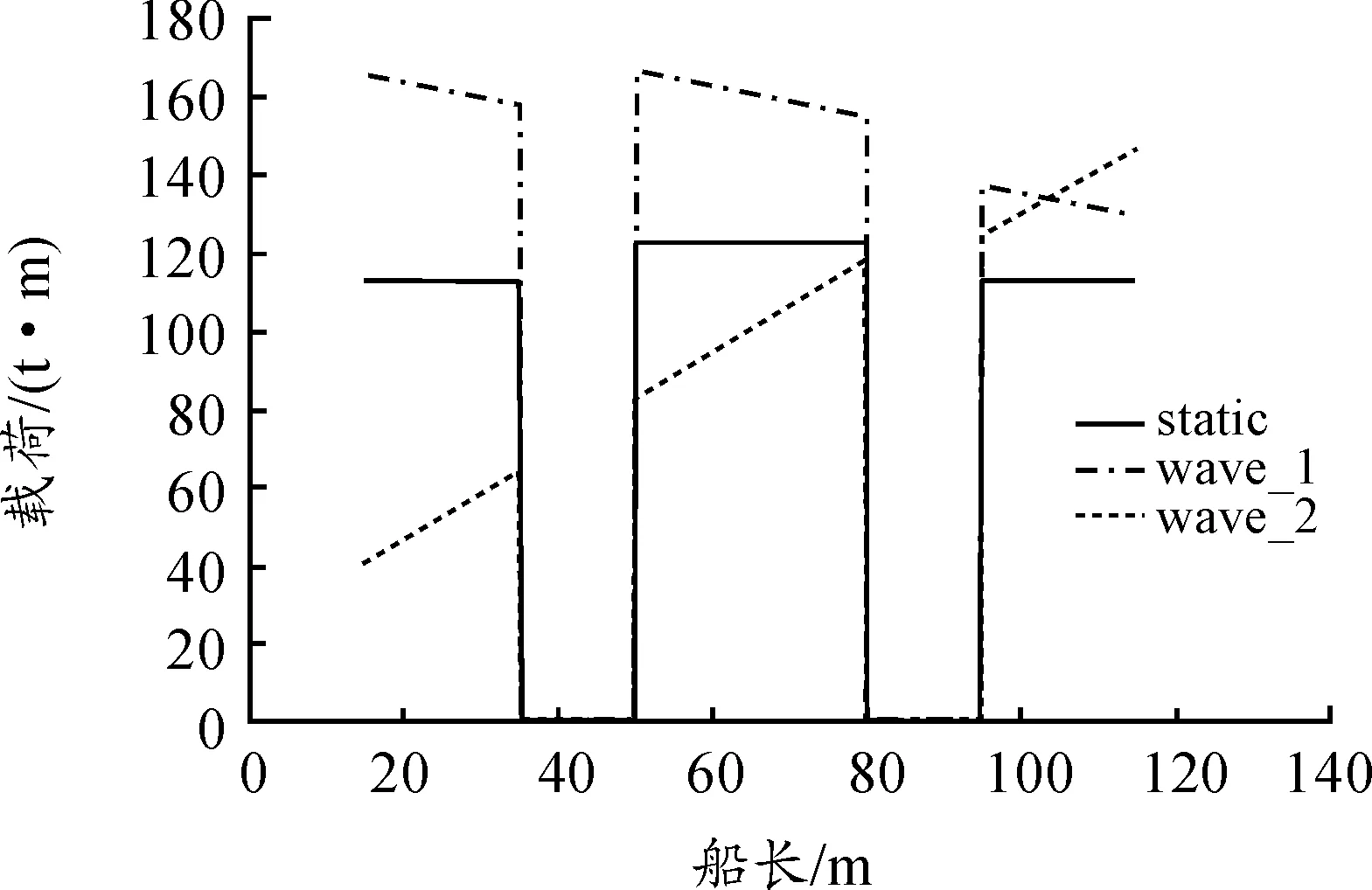
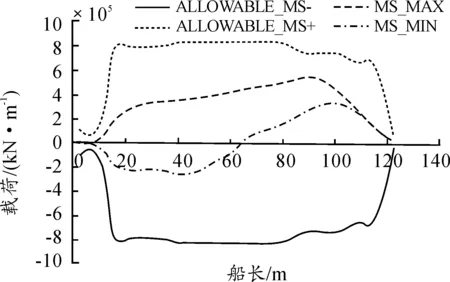
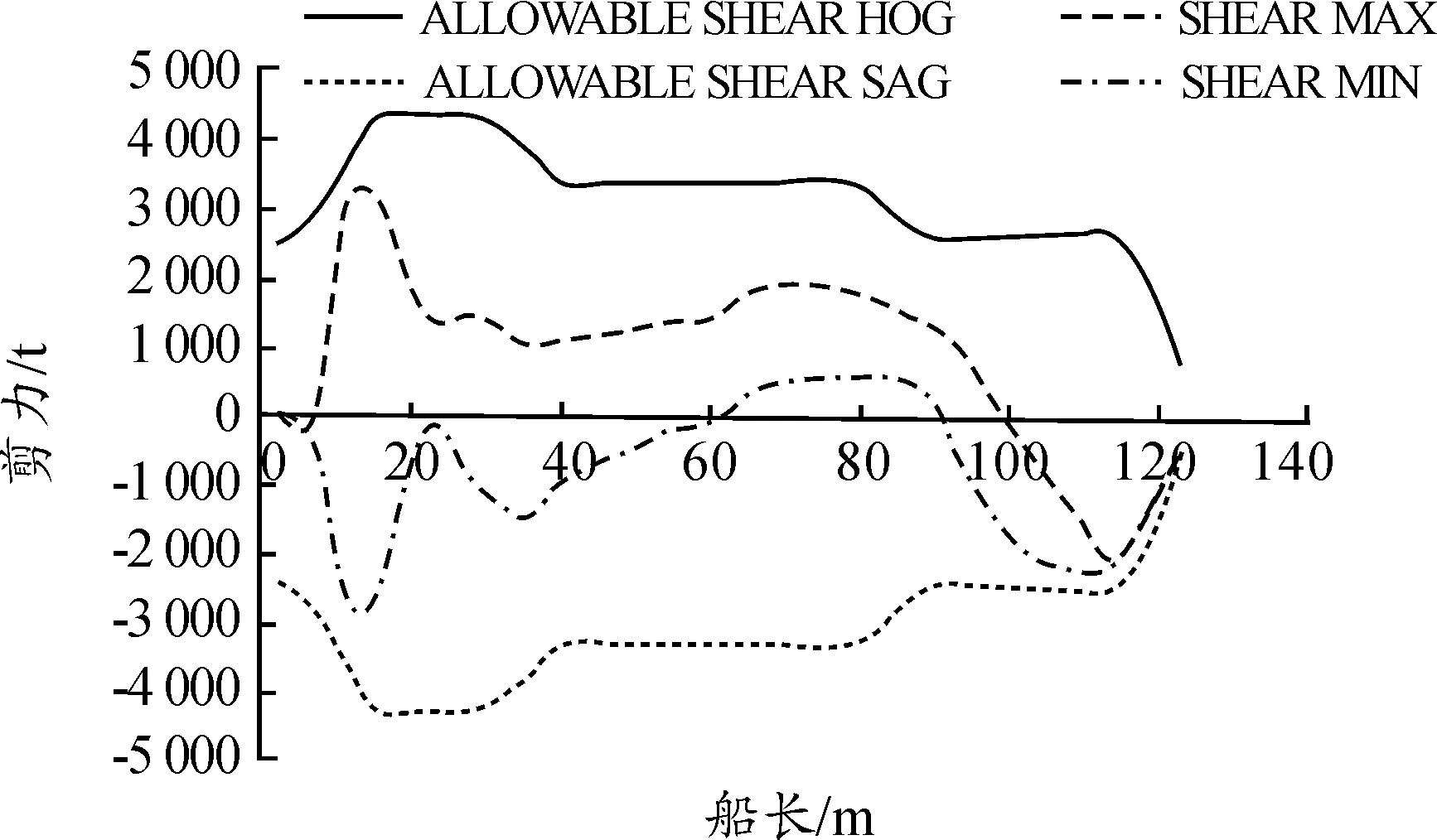
引入迭代因子gj(j=1,2,…,m,0 且: 式中:Li,1、Li,2分别为第i个坐底分段的尾端、首端沿船长方向距船体尾封板的距离。 以gj=0.50为初始值示例,其变化值为±0.001的迭代步进行依次迭代求解,分别求解载荷相关因子:ai,1、bi,1;直到ai, j、bi, j能够满足静载荷平衡容许误差及静载荷积分矩平衡误差均在0.1%以内: 以上均为船体坐底反力沿船长方向的分步计算求解,沿船宽方向的坐底反力分布求解与船长方向理论一致,最终均为垂向静载荷及静载荷沿相应力矩方向的积分矩平衡为基本方程,并以工程允许的迭代误差来评判所求解的对地反力实现迭代收敛。 最终,对地载荷以垂向面载荷的形式,沿船长、船宽方向呈三维分布: p(x,y)=fi(x)×fi(y) 以本目标工程驳船典型设计工况为例,船底平底段沿船长为距尾端15~115 m范围,船宽平底段宽为29 m,见图1。本目标工程驳船为改造船工程,坐底海域海底分布较为复杂,因而最终经实地测绘后确定的设计坐底工况也较多,而且本船船体承载能力有限,且要求全回转吊起重设计能力,起初仅多段式坐底工况就已达11种之多,而且目标作业海域海况相对恶劣,本船总体初步配载是在反反复复校验中以总体性能、船体能力、环境载荷为三大设计目标,三方共同努力协调下经过无数次的反复后才最终确定。 本文以较为良好的三段式坐底工况作为计算示例,见图1,注意的是多段式坐底工况的数目多少影响的仅是数据量的多寡,目标工程可承受环境载荷的范围大小,但基本原理均相同。 静水载荷[5-6,9-10]作用下的对地载荷求解,只需依据初步的船体质量分布、装载分布、浮力分布通过上节的理论基础公式,编写Microsoft/Excel迭代语言程序求解坐底载荷及其分布,见图2;然后依据坐底载荷分布的规律调整本船不同作业状态的配载达到设计目标的坐底载荷分布。本目标工程船在配载设计中就已通过横向配载使得横向的对地载荷分布均匀。 图2 对地载荷沿船长分布示意图 自编Microsoft/Excel迭代语言程序与最终经NAPA程序微调后的数据比较如图3所示;需要注意的是,本目标改造工程驳船因为船体承载能力有限,总体配载限定为几乎平浮状态,如果初步的船体配载并非平浮状态,而是有一定的首尾倾,那么自编Microsoft/Excel迭代语言程序与经NAPA程序模拟得到的对地载荷是存在一定差异的,因NAPA程序模拟得到的是分段式均匀载荷,而不能实现分段式阶梯分布载荷(见图4)。 图3 平浮配载的对地载荷比较 值得注意的是,如果拟设计工程不需要平浮配载的话,那么本计算方法在用于NAPA商用程序时可通过模拟在原多段式基础上再增分为无数个小的分段式均匀载荷来近似模拟由Microsoft/Excel迭代语言程序得到的对地载荷分布。 图4 非平浮配载的对地载荷比较 波浪载荷下对地载荷求解的困难在于波浪外载荷时历变化下,船型结构物受到的浮力、纵横倾力矩等相关波浪载荷的确定,且均为时历变化值;若初始设计时,设计外载荷环境相对确定,那么波浪载荷下对地载荷求解就相对方便些。船型结构物波浪载荷下的对地载荷求解主要目的在于扫描到本船在动载荷影响下的对地载荷极值,进而开展船体结构强度设计。本目标工程驳船为改造船,船体承载能力有限,导致对地载荷极值是限定值,因而是反过来控制波浪环境以满足工程设计的各方面需求。 本目标工程驳船采用模型试验[2,4,8]的方法得到波浪载荷下的垂向浮力变化值、纵横倾力矩等波浪环境数值,因而,波浪载荷下的对地载荷求解相对较为简单,只需要利用Microsoft/Excel迭代语言程序,依据不同分段位置,满足上述的力学平衡方程的理论基础上,求解不同分段的对地载荷即可(见图5)。 图5 波浪载荷下对地载荷分布示意图 坐底式船型结构物船体装载优化的目的是尽可能最大程度的发挥压载水舱调载能力,使得静水载荷时的船体对地载荷分布较为均匀,以最大程度的减小因波浪载荷等动载荷变化而引起的对地载荷突变可能发生的船体结构破坏。本目标工程船经过优化后的船体配载严格保持了对地载荷沿坐底范围内均匀,静水弯矩与静水剪力的包络值与许用静水载荷的比较如图6和图7所示。 图6 静水弯矩比较示意图 图7 静水剪力比较示意图 1) 目标改造驳船的多分段对地载荷求解在刚体力学理论基础上,借助Microsoft/Excel迭代语言程序实现,成功克服了目前通用总体配载软件在多分段坐底船型结构物工程设计上的困难; 2) 目标改造驳船的多分段对地载荷求解通过Microsoft/Excel迭代语言程序与NAPA商用总体配载程序相互验证,保障了对地载荷求解的正确性和船体总体配载的有据可依。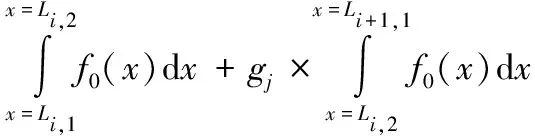
1.3 坐底载荷复核
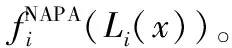
2 静水载荷下对地载荷求解
3 波浪载荷下对地载荷求解
4 船体装载优化
5 结论

