基于DRNN的多回路参数在线自整定控制解耦算法

肖宏启

(贵州航天职业技术学院 计算机科学系， 贵州 遵义 563000)

在航空航天、军工以及核工业等多个工业控制领域，因系统中存在诸多复杂不确定性因素(如各控制回路间存在关联耦合等)，用数学手段精确描述被控对象动态特性变得非常复杂，即使克服了数学建模的困难，因所建数学模型计算复杂度高，也很难实施精准的范式控制，因此复杂关联耦合系统的控制变成了工业控制领域中的老大难问题。尽管控制难度高，但是通过学者的艰苦努力，近年来在应用研究领域还是取得了多项可喜的研究成果[1-8]，它们的共同特点是对控制系统实施解耦的控制策略，针对不同的对象特性寻找合适的控制律与现场工况条件匹配，使系统解耦后的每个系统输出只由一个唯一的系统输入控制，借此消除不同控制回路之间的相互影响从而提高对关联耦合系统的控制品质[9-10]。鉴于解耦方法的多样性，因此，有必要对关联耦合系统的控制策略进行深入研究。

1 耦合系统的控制难点与控制策略

1.1 控制中存在的问题及其求解思路

多回路耦合系统属复杂关联系统范畴，系统中变量众多，关系复杂，控制中存在的问题主要表现在：

1) 耦合系统中控制参数众多，关系复杂，控制参数往往在某个范围内变化，因其存在不确定性，难以进行精确数学建模，即使通过系统参数辩识方法获得了控制参数，也是难于实施精准数学建模的范式控制的，采用传统PID控制方法几乎不可能对这类耦合系统实现有效的精准控制，因其失去了采用传统PID控制的数学建模前提条件，因此需要研究新的控制策略。

2) 控制耦合回路参数往往存在非线性，由于非线性处理方法非常复杂，难以采用量化的数学方法描述，一旦数学模型有偏差，控制系统的稳定运行条件就可能被破坏，引起控制系统失稳，甚至导致控制系统崩溃，因此采用传统范式控制策略是不可取的。

3) 复杂耦合多回路系统的各个控制要素之间既高度耦合又是相互制约，其组成往往是半结构化或者非结构化的，在复杂外部电磁干扰环境下，传统控制方法缺乏有效解决控制问题的手段，因此很难采用传统控制方法实施有效控制。

从上述可知，采用一般意义下的PID控制及其变形如智能PID控制等传统策略对复杂多回路耦合控制系统实现高品质控制是非常困难的。针对存在问题，有必要探讨新的控制策略。求解控制问题的思路是：首先对复杂耦合多回路系统实施解耦，然后，将不确定性、非线性与外部干扰等难于解决的瓶颈问题，采用人工智能中的神经网络控制方法求解。由于神经网络拥有非常强大的泛化与非线性处理能力，因此是一种值得探讨的解决问题的控制策略。

1.2 解耦控制策略

在现代工业过程控制系统中，系统解耦是指多变量系统的每个输出只能由一个相应的输入唯一控制，同时每个输入也只能控制一个相应的输出。随着控制理论的发展，出现了种解耦的控制方法，从理论分析角度可以将其划分为基于Morgan问题的解耦、基于特征结构配置的解耦和基于H∞的解耦等多种控制方法，本文聚焦于将一个相互关联交叉耦合的多输入多输出控制系统分解为多个相互独立的单变量控制系统，然后分别对各个控制回路实现自治的控制，采用对角回归神经网络DRNN(Diagonal Regression Neural Network)作前馈解耦补偿器，即在控制对象的前端连接一个DRNN网络使系统传递函数矩阵简化为一个简单的对角函数矩阵，将一个多输入多输出系统的控制转换为单输入单输出系统的控制问题，从而实现对多输入多输出交叉耦合系统解耦控制。DRNN是一个神经网络的计算模型，拥有非常强大的并行计算、非线性、不确定性和自学习等处理能力，特别值得注意是：DRNN中包含有回归神经网络RNN(Recurrent Neural Network)，因其具有内部反馈功能可直接反映整个神经网络的动态特性，实质上位于对角回归神经网络的隐藏层就是一个回递层，借助DRNN网络对杂关联耦合系统的解耦就可降低控制难度，简化控制算法的计算复杂度，并在实现解耦的同时自动整定控制参数，借以提高对关联耦合系统的控制品质，以下推导复杂交叉耦合系统的解耦控制算法。

2 基于DRNN的解耦控制算法

2.1 基于DRNN的前馈补偿器

DRNN本身是一个前馈神经网络，如图1所示，其组成结构可划分为输入、隐藏和输出等3个层，图中的隐藏层实际上是一个回归神经网络，如图1的右上角所示。

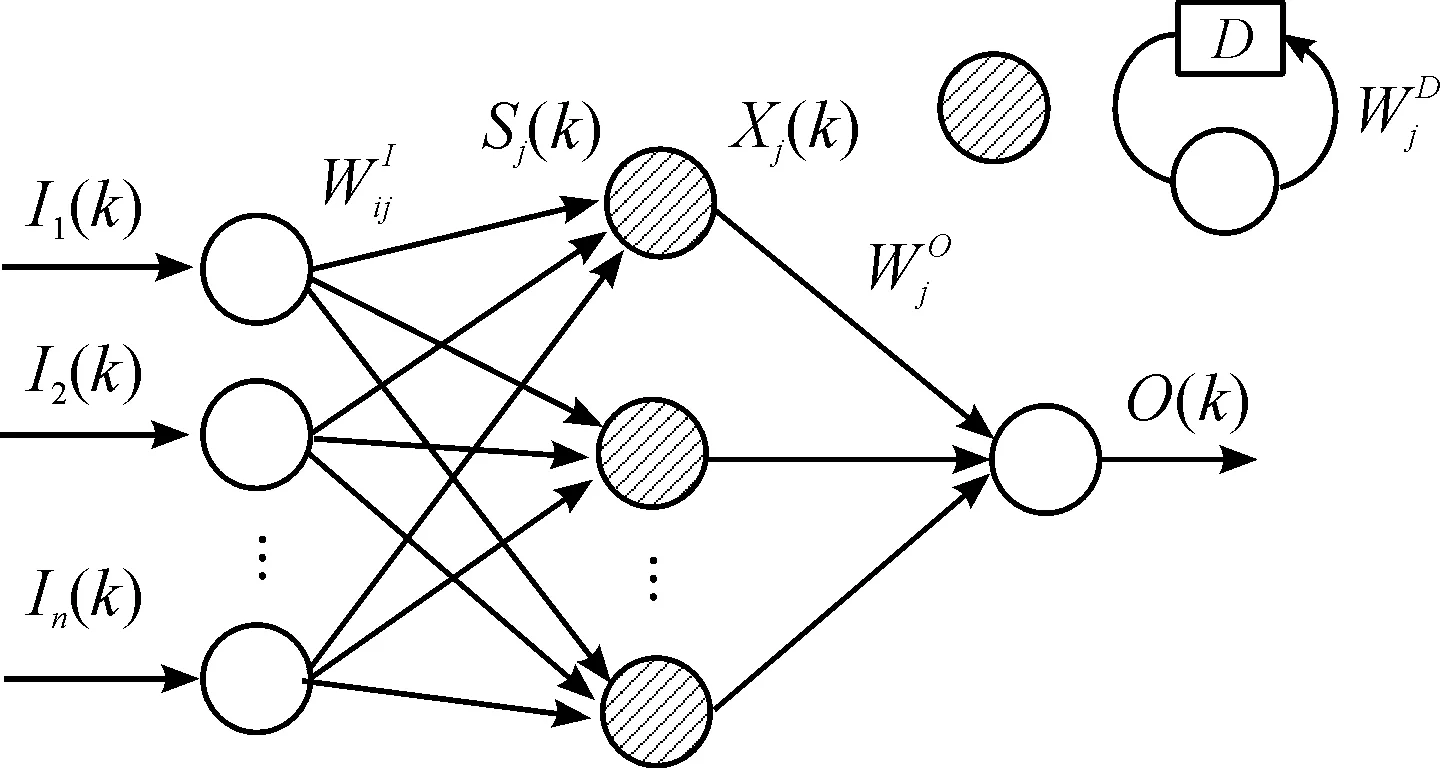
图1 DRNN结构

图1中，I=[I1，I2，…，In] 表示输入矢量，O(k)为DRNN网络的输出，Ii(k)，f(·)，Xj(k) 分别为输入层的第i个神经元，回归层激励的S函数和第j个神经元输出。

DRNN的输出如式(1)所示。

(1)

式(1)中，Wjo表示输出层的权重矢量。

回归层的输入如式(2)所示。

(2)

回归层的输出如式(3)所示。

Xj(k)=f(Sj(k))

(3)

图2表示了网络状态辩识器的结构，其功能是在线辩识被控对象的动态特性，借助在线训练，可获得近似于实际系统的同步辨识结果输出。

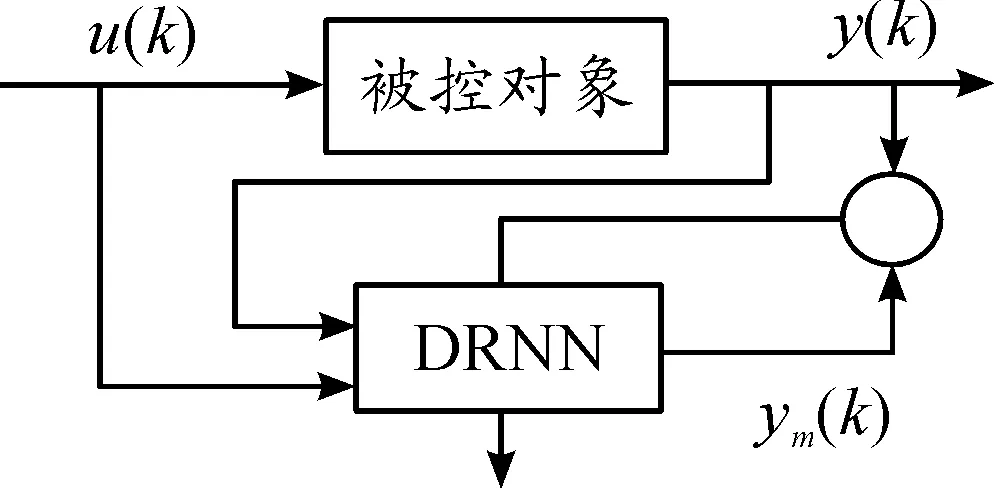
图2 网络辩识器结构简图

图2中，u(k)和y(k)分别为被控对象的输入和输出。DRNN的输入为u(k) 和y(k)，ym(k) 是网络辩识器的输出，并且满足ym(k)=o(k)，辩识误差em(k) 和辩识指标的表达式分别如式(4)和式(5)所示。

em(k)=y(k)-ym(k)

(4)

(5)

2.2 基于DRNN的权值优化学习算法

在计算过程中，优化学习采用梯度下降法与动量因子相结合的算法，其输入层、递归层和输出层的权重分别如式(6)、式(7)和式(8)所示。

(6)

(7)

(8)

在式(6)、式(7)和式(8)中，回归层神经元采用双s形函数，即选取f(x)为(1-e-x)/(1+e-x)，ηI为输入层的学习速率，ηD和ηO分别回归层的学习速率和输出层的学习速率，α是惯性系数。

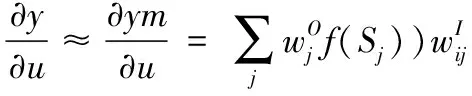
(9)

在学习中，如果分别将位于输入、回归和输出层的学习速率增大，则会加快收敛速度，但可能导致系统更易于产生振荡和不稳定。如果降低学习率又可能影响算法的稳定性，并导致收敛速度为负加速度。因此如何选择学习速率是值得关注的，要根据实际情况而定。注意，当∂Em(k) /∂w=0时，通过计算获得的加权梯度值仅仅是为一个局部极值点，如动量因子采用惯性系数，也就是说，如将惯性系数作为动量因子，那么在计算的最后一步，权值的修正将由权值变化增量值和梯度值两者共同决定。

2.3 基于DRNN改进的参数自整定解耦控制算法

上述讨论了采用DRNN对交叉耦合系统实施解耦的控制问题，是否可以在实现解耦的同时也将控制器的控制参数进行优化以获得更好的控制品质呢？如果将DRNN解耦与控制器参数整定方法融合，采用基于DRNN改进的自整定解耦控制算法就可实现在解耦计算的同时也完成对控制参数的优化自整定。例如，对双输入双输出被控对象而言，如采用如图3所示的控制系统结构，仍然采用PID控制，则其解耦控制算法如式(10)所示。

(10)

式(10)中，T为采样时间，其中：

error1(k)=r1(k)-y1(k)，error2(k)=r2(k)-y2(k)

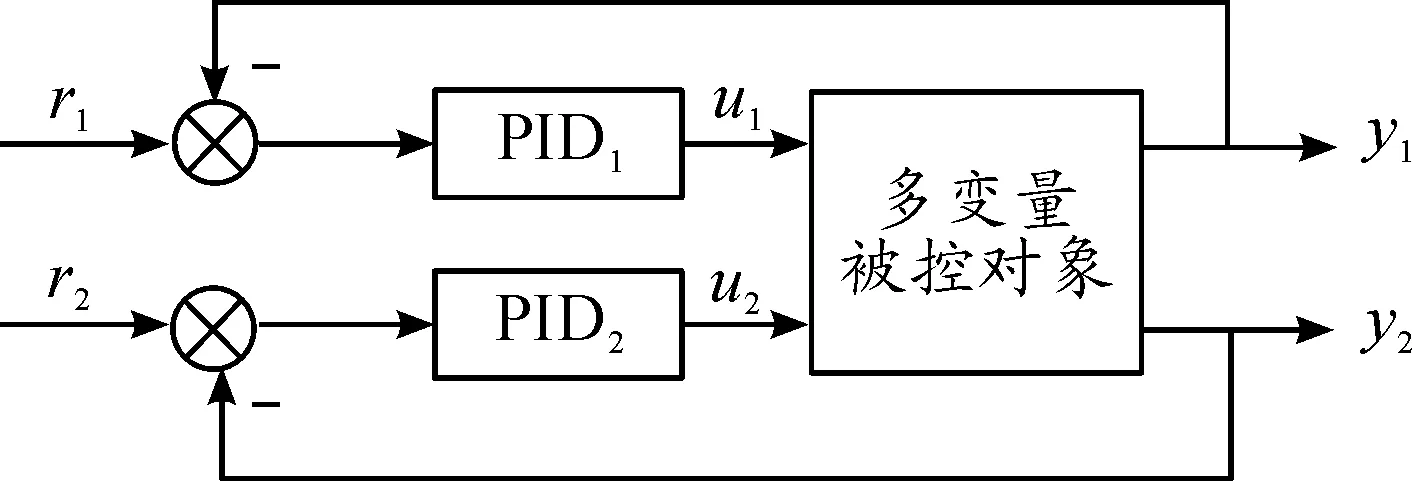
图3 PID解耦控制结构简图

改进算法有助于PID解耦控制参数的自整定，其控制系统结构如图4所示。

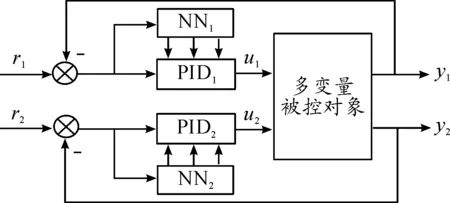
图4 基于DRNN的PID自整定系统结构简图

DRNN由DRNN1和DRNN2组成，y、r分别表示实际系统输出值和系统的给定值。由于控制通道1和控制通道2相似，以下仅以通道1为例讨论相应的控制算法。对控制通道1有：

(11)

式(11)中，error1(k)=r1(k)-y1(k)

PID控制器通过对DRNN的计算，自动调整PID控制器中比例系数、积分系数和微分系数的控制参数。注意，在整定过程中，输入是PID控制器前一个周期的控制参数，输出是PID控制器当前的控制参数。参数修改结构如图5所示。

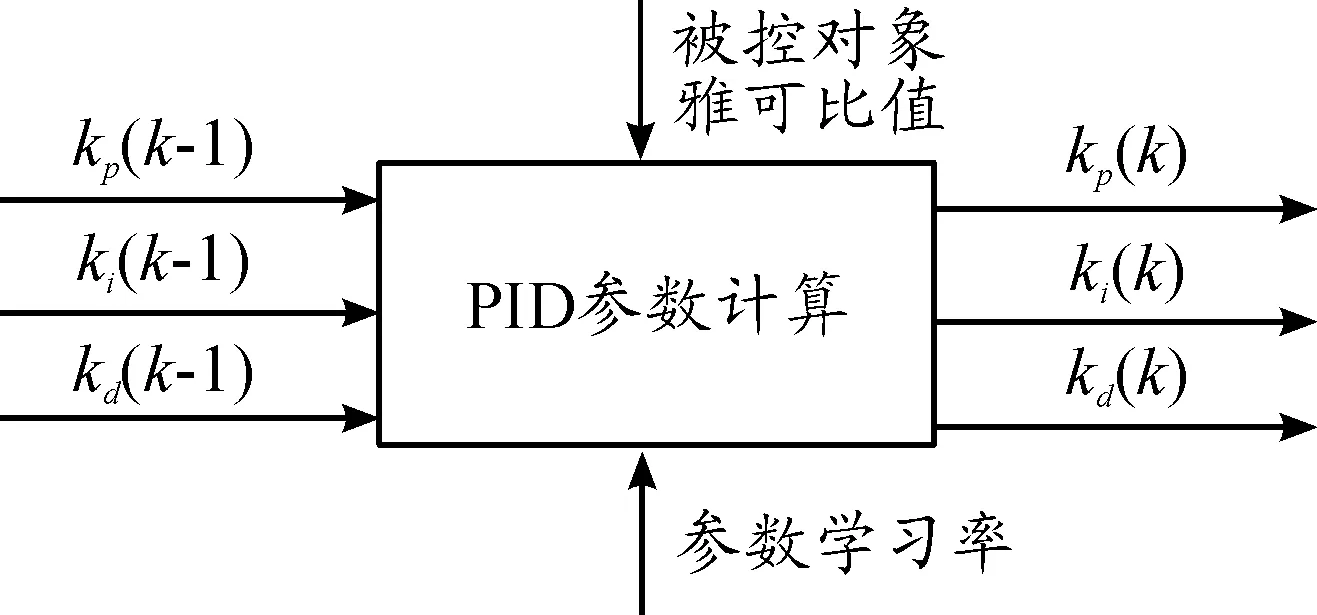
图5 PID控制器的参数修改结构简图

一般选择的评价指标值如式(12)所示，即：

(12)

PID控制器中3个控制参数的整定表达式分别为：比例系数采用式(13)，积分系数采用式(14)，微分系数采用式(15)。

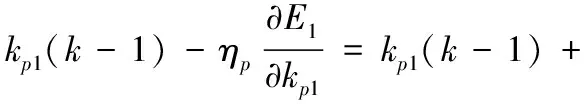
(13)

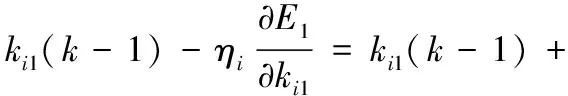
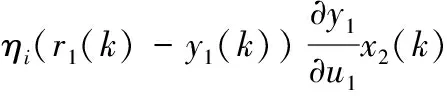
(14)

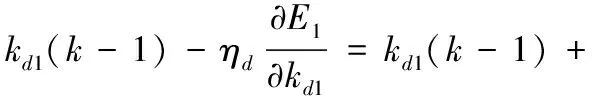
(15)

每个参数的自学习调节率都与kp1(k)，ki1(k) 和kd1(k)的调节参数直接相关，通常选择调节率为不变常数。但其大小与误差偏差量和误差偏差量变化率直接相关，因此PID控制器参数的学习调整率定义如式(16)、式(17)和式(18)所示。

ηp(k)=ηp(k-1)+p1·e(k)+

p2·(e(k)-e(k-1))/T

(16)

ηi(k)=ηi(k-1)+i1·e(k)+

i2·(e(k)-e(k-1))/T

(17)

ηd(k)=ηd(k-1)+d1·e(k)+

d2·(e(k)-e(k-1))/T

(18)

根据上述学习调节率定义，可以认为它是随着系统误差和误差变化率的变化而变化的，从而使之达到最佳的控制效果。同样，通道2的调节原理与控制通道1类似，这里就不再讨论了。

3 实验仿真及其结果分析

3.1 实验仿真

3.1.1实验仿真数学模型

现以某军用弹药仓库库房的温、湿度控制为例，因库房内的温、湿度是相互关联耦合的，图6为HVAC系统在冬季温、湿度控制单元的结构示意图，因温控比湿控系统的时间常数Th大，因此温度在控制过程中扮演主导角色。

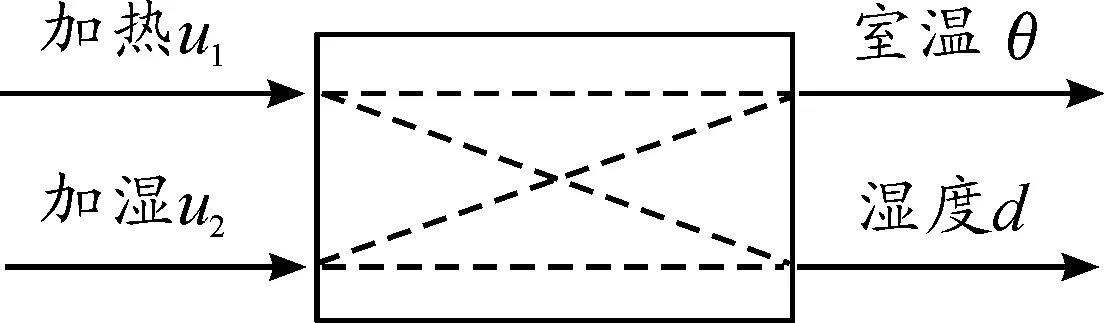
图6 冬季的单元耦合对象模型结构示意图

库房温、湿度分别用θ、d表示，其系统模型可用矩阵形式表示为式(19)

(19)

如果将式(19)中的u1和u2分别换为r1和r2，根据实际测试的实验仿真数学模型如式(20)。

(20)

由式(20)可知，只有对HVAC控制系统实施温、湿度解耦，才有可能对军用弹药仓库库房实现高精度的温、湿度控制。

3.1.2实验仿真

实验仿真中，采用图4结构对HVAC系统进行控制，设计的网络结构为3-7-1，输入取为I={u(k-1)，y(k)，1}，采样周期选取为5 s，输入层学习速率选取为0.4，回归和输出层的α值选取为0.04，初始权重选择为[-1，1] 区间上的一个随机值。

首先讨论加热器入口速度对库房内温度和湿度的影响。设r1为单位阶跃，即r1=1，取r2=0，由式(13)、式(14)和式(15)可知，只要确知其雅克比值，即系统输出对系统输入求偏导的值，就可以获得PID的3个控制参数，在Matlab环境下，随时间t变化的雅可比值曲线如图7所示。表1为调整前后的PID控制参数值，图8为控制解耦后的控制过程响应曲线。

按照与上述同样的方式，设r2为单位阶跃，即r2=1，取r1=0，在Matlab环境下，调整前后的PID控制参数值如表1所示，图9为随时间t变化的雅可比值曲线，图10为控制解耦后得到的控制过程响应曲线。

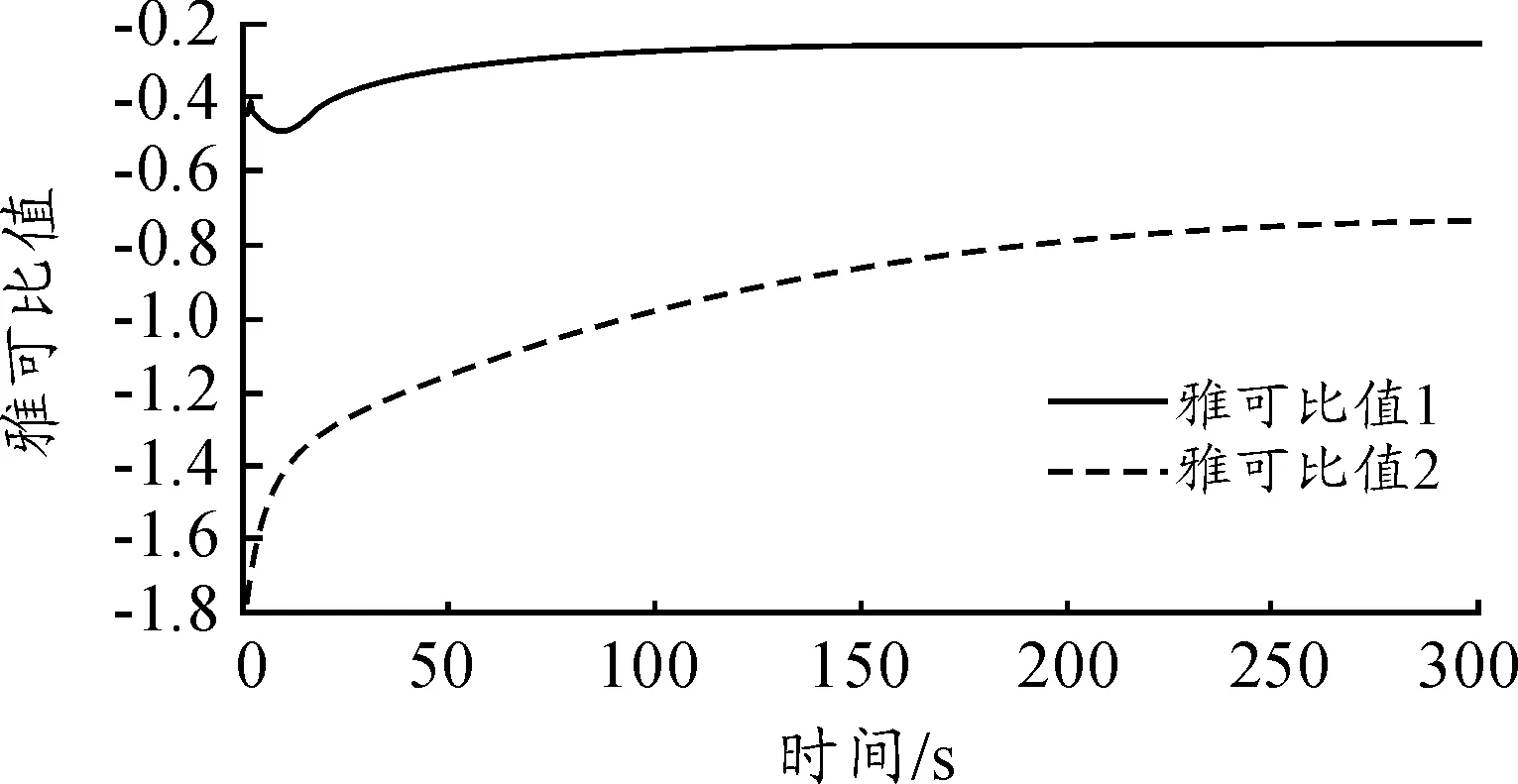
图7 DRNN1的雅可比值曲线

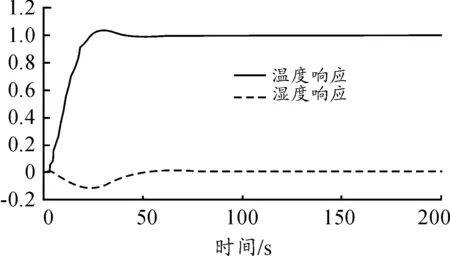
图8 PID控制解耦后的响应曲线

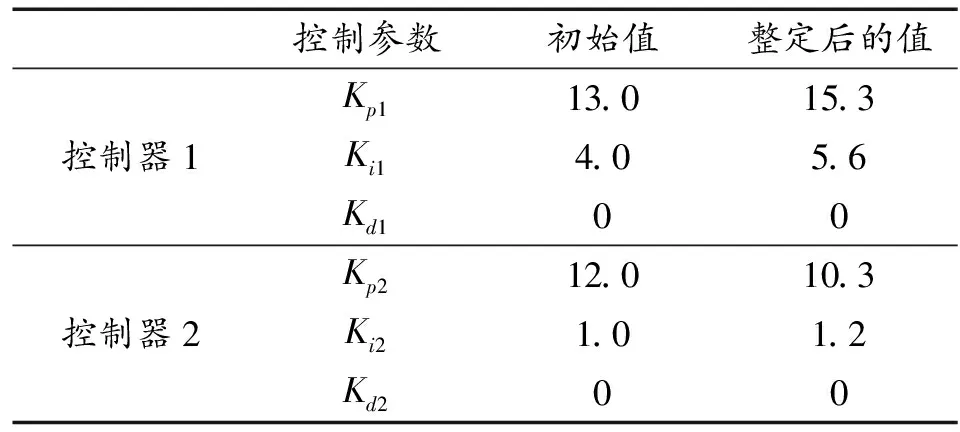
表1 PID控制参数

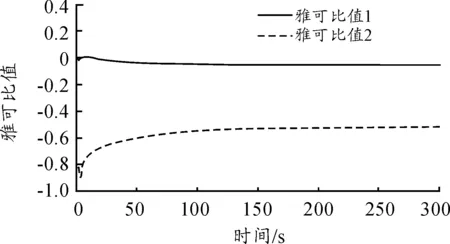
图9 DRNN2的雅可比值曲线

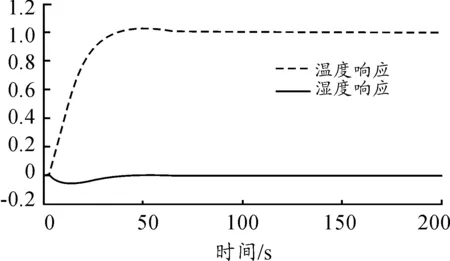
图10 PID控制解耦后的响应曲线

3.2 仿真结果分析

分析图8和图10可知，在单位阶跃输入条件下，经过控制解耦后，湿度环耦合效应显著减小，在短时间内相互影响迅速衰减为零，达到减湿效果，缩短了温度上升时间。从上述实验仿真结果可见，对于某军用弹药仓库库房的温、湿度控制，采用基于DRNN改进的控制参数自整定解耦控制算法是可以获得令人满意的温、湿度解耦控制效果的。

4 结论

对相互关联的多回路耦合系统，利用RNN的独特优势，采用基于DRNN改进的多回路参数自整定PID解耦控制算法，可以实现对多回路解耦的控制参数自整定控制。仿真结果验证了改进算法的合理性、可行性和有效性，为复杂关联耦合系统提供了另一种解耦控制方案。