基于事件触发的多智能体系统编队控制

周绍磊，赵学远，王帅磊，祁亚辉

(海军航空大学， 山东 烟台 264001)

近年来，随着多智能体系统一致性问题的研究日益深入，将多智能体系统一致性的分布式控制思想及方法，应用到多智能体编队控制中也取得了大量成果[1-3]。文献[4]中利用多智能体之间相对距离信息，基于鸽群行为设计了最优编队控制器，使得系统形成编队，并在复杂运动下能够有效地保持编队队形。文献[5]中利用一致性思想设计了控制器，使得一类特殊的高阶系统形成编队。为了解决离散的多智能体系统编队控制问题，文献[6]中设计了一致性分布式控制器。在无向图下，文献[7]中为二阶系统设计了分布式控制器，使其能够形成编队。虽然以上文献，为了实现编队控制，所采用的都是一致性的方法和思想，但是所设计的控制都要求通信拓扑保持实时无线通信。如文献[8]所述，这种通信方式占用传感器70%的能源，不仅浪费通信带宽，而且也消耗了大量计算资源。因此，将文献[9]中提出的事件触发的控制策略应用到多智能体的编队控制当中，能够有效地降低传感器对于高频数据采集的要求，在两次事件触发的时间间隔内，多智能体系统不需要进行通讯，能量消耗大幅降低，整个系统能够更高效地完成任务。基于事件触发的编队控制问题在文献[10-12]中也有所研究，但与之不同的是，本文研究的是有向拓扑条件下的，多智能体编队控制问题，提出了一种新的解决事件触发下多智能体系统编队控制问题的解决方案，利用Laplacian矩阵的特殊性质，将高阶系统编队控制问题简化为了低阶系统的渐近稳定性问题。

1 预备知识

引理1[13]拓扑图G的Laplacian矩阵L至少有一个零特征值，其他非零特征值均具有正实部；如果有向图G包含有一个有向生成树，则0是L的简单特征值，1N是其对应的右特征向量。

引理2[14]对于图的Laplacian矩阵L∈RN×N，那么存在一个矩阵M∈RN×N-1使得L=ME，其中E∈R(N-1))×N，其特定形式为

进一步，如果图包含一个有向生成树，那么矩阵M是列满秩的,且矩阵EM的特征值是L的非零特征值，则Re(λ(EM))>0。

2 问题描述

考虑N个多智能体构成的多智能体系统，其中每个智能体的运动模型描述如下

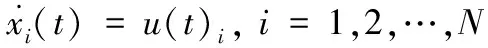
(1)

其中，xi∈Rn，ui∈Rp分别为第i个智能体的系统状态和控制输入。

定义1：对于多智能体系统(1)和任意的初始状态，如果存在一个控制器使得

(2)

成立，则称多智能体系统(1)能够形成编队。其中hi(t)表示多智能体系统的编队队形，即每个智能体xi(t)的期望状态，本文所研究的编队队形hi(t)为时变编队队形，相比于固定编队更具有意义。

本研究把基于事件触发函数设计一个控制器，使得多智能体系统的状态满足定义1作为主要研究问题。事件触发函数的设计多智能体系统仅在事件触发函数等于零的时刻进行通信，降低了多智能体系统的通信频率。

3 控制器设计

仅依靠邻居智能体之间的相对状态信息，基于事件驱动的多智能体系统一致性分布式控制器按如下设计

(xi(tk)-hi(t))]+wi(t)

(3)

其中：tk为系统第k次事件触发时刻，k=0,1,2,…,wi为待设计的辅助控制输入函数。当事件未触发时，系统内部无线通信保持静默状态；事件触发时，多智能体系统内部按照相关通信拓扑图进行通信，这样有效地节省了通信带宽和计算资源，所需要的事件触发函数在后文进行设计。

将式(3)代入式(1)可得

(xi(tk)-hi(t))]+wi(t)

(4)

进一步整理可得

(IN⊗In)w(t)

(5)

令θi(t)=xi(t)-hi(t)可得

(6)

其中θj(tk)=xj(tk)-hj(t)，θi(tk)=xi(tk)-hi(t)

进一步整理可得

(7)

定义状态误差

ei(t)=xi(tk)-xi(t)

(8)

将其代入式(7)可得

(9)

因此当

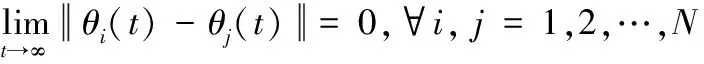
(10)

时系统(1)形成编队。至此系统(1)的编队控制问题转化为系统式(9)的一致性问题。

令

(11)

则有

(12)

因此可以得到

(EM⊗In)ξ(t)-(E⊗In)w(t)

(13)

所以

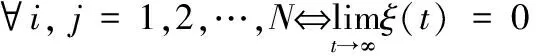
(14)

故多智能体系统(1)能够形成编队h(t)的充要条件是

(15)

且系统

(16)

是渐进稳定的。

引理3：在采用基于事件驱动的一致性控制器(3)作用下，系统(1)能够形成编队h(t)，当事件触发函数为

(17)

其中λ为(EM)⊗In的最小特征值。||·||为矩阵范数，其中δ为常数，且满足0<δ<1。

证明：构造李雅普诺夫函数

V(t)=ξ(t)Tξ(t)

(18)

对式(18)沿着系统(16)求导可得

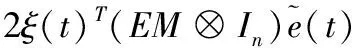
(19)

根据引理2可知λ>0，因此

(20)

即

(21)

所以

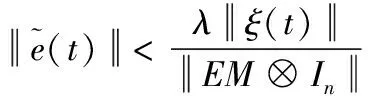
(22)

令

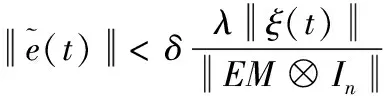
(23)

将式(23)代入式(20)可得

(24)

因此所设计的事件驱动函数(17)能够使得系统(16)渐进稳定，此时即系统(1)能够形成编队h(t)。

引理4：根据引理3所设计的事件驱动函数，不存在Zeno现象，即两次事件驱动的时间间隔严格大于0，其最小时间间隔为

(25)

证明：类比文献[15]由式(23)可得

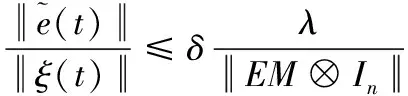
(26)

因此可得

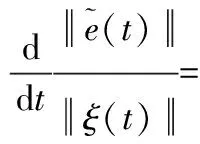
(27)

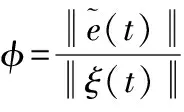
则有

(28)

因此事件驱动的时间间隔与φ的增长速率成正比。故φ的增长速率达到最大值当且仅当

(29)

令φ(t,φ0)为当初始值为φ0，在时刻t的值。设φ(t,0)是式(29)的解。求解可以得到

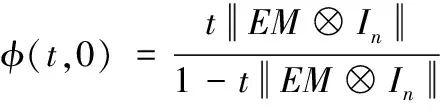
(30)

在式(30)中，φ的增长速率最大，为了求解最短的事件触发时间间隔Δtmin，将其代入式(23)，取等号，求得

证毕。

4 仿真验证

考虑在三维运动的4架无人机构成的多智能体系统，其中动力学模型由式(1)描述，xi表示第i架无人机位置信息，ui表示第i架无人机的控制输入。无人机之间通信拓扑结构如图1所示。

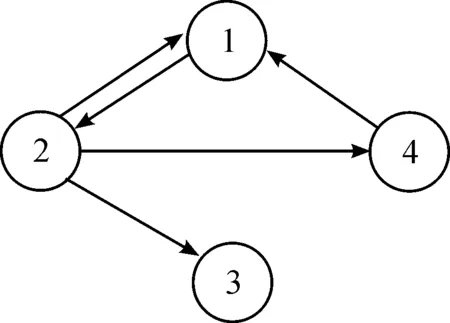
图1 通信拓扑图

由通信拓扑结构，得到Laplacian矩阵为

无人机初始状态为

xi1,xi2,xi3代表第i架无人机在三维坐标系中x轴坐标，y轴坐标，z轴坐标。

编队队形设计为

其中hi1(t)、hi2(t)、hi3(t)表示第i个智能体的期望编队。

在控制器(3)的作用下，4架无人机构成的系统能够形成编队，当编队形成时，系统第一个状态与编队之间误差随时间变化如图2所示，其余两个状态与编队误差与之相似，故在此不予展示。

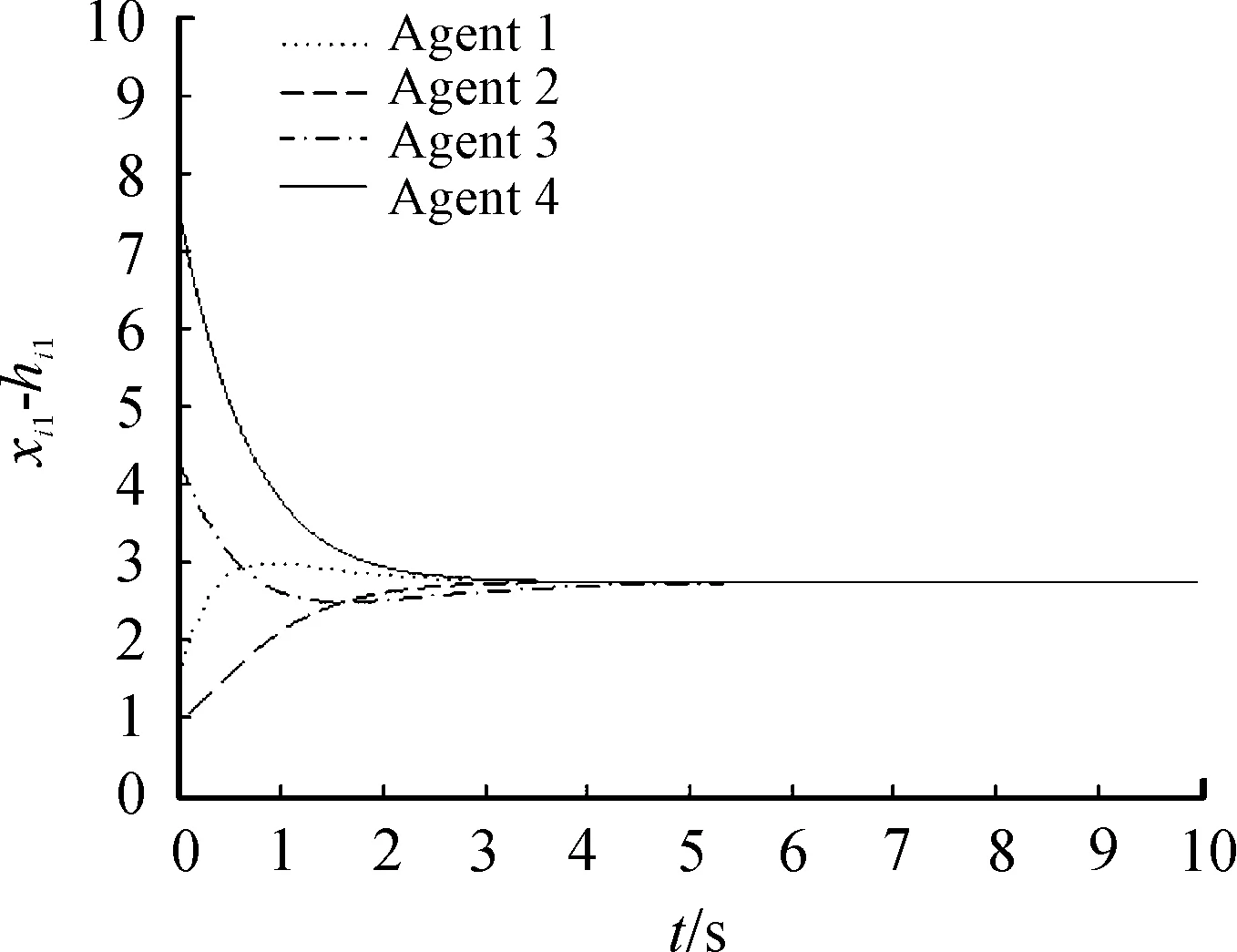
图2 系统状态与编队误差xi1-hi1, i=1,2,3,4

结合图2分析，4架无人机在5.5 s时系统状态与所要实现的编队状态误差达成一致，此后一直保持一致状态，根据定义1可以知道编队能够形成。

图3～图5分别为4架无人机在t=2 s，t=5.5 s，t=20 s三维空间中形成的编队。

通过x的三维状态，将4架无人机在三维空间位置呈现在图3～图5。对图2的分析，可知在5.5 s时，系统形成编队，因此当5.5 s时，图4上的4架无人机系统在三维空间中形成平行四边形编队，图3为2 s时4架无人机在三维空间位置，明显看出其未形成平行四边形，即仍未达成编队。由于本文设计的编队为时变编队，因此随着时间的变化，无人机系统形成的编队队形也是时变的，对比20 s(图5)时和5.5 s(图4)时4架无人机位置可知，4架队形均为平行四边形，但是两个平行四边形对应顶点位置的无人机不同，即编队队形为时变的平行四边形。

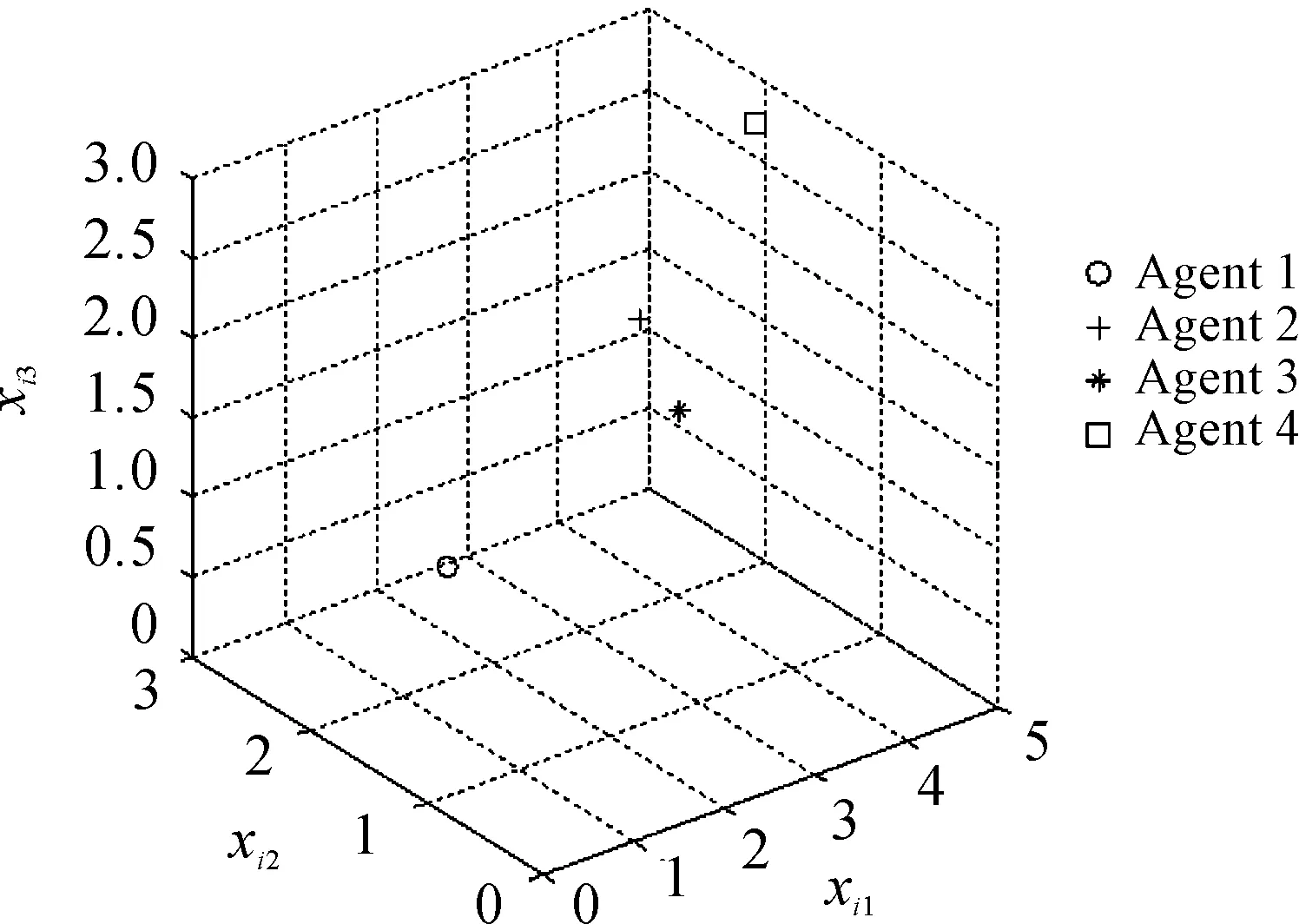
图3 t=2 s时编队队形

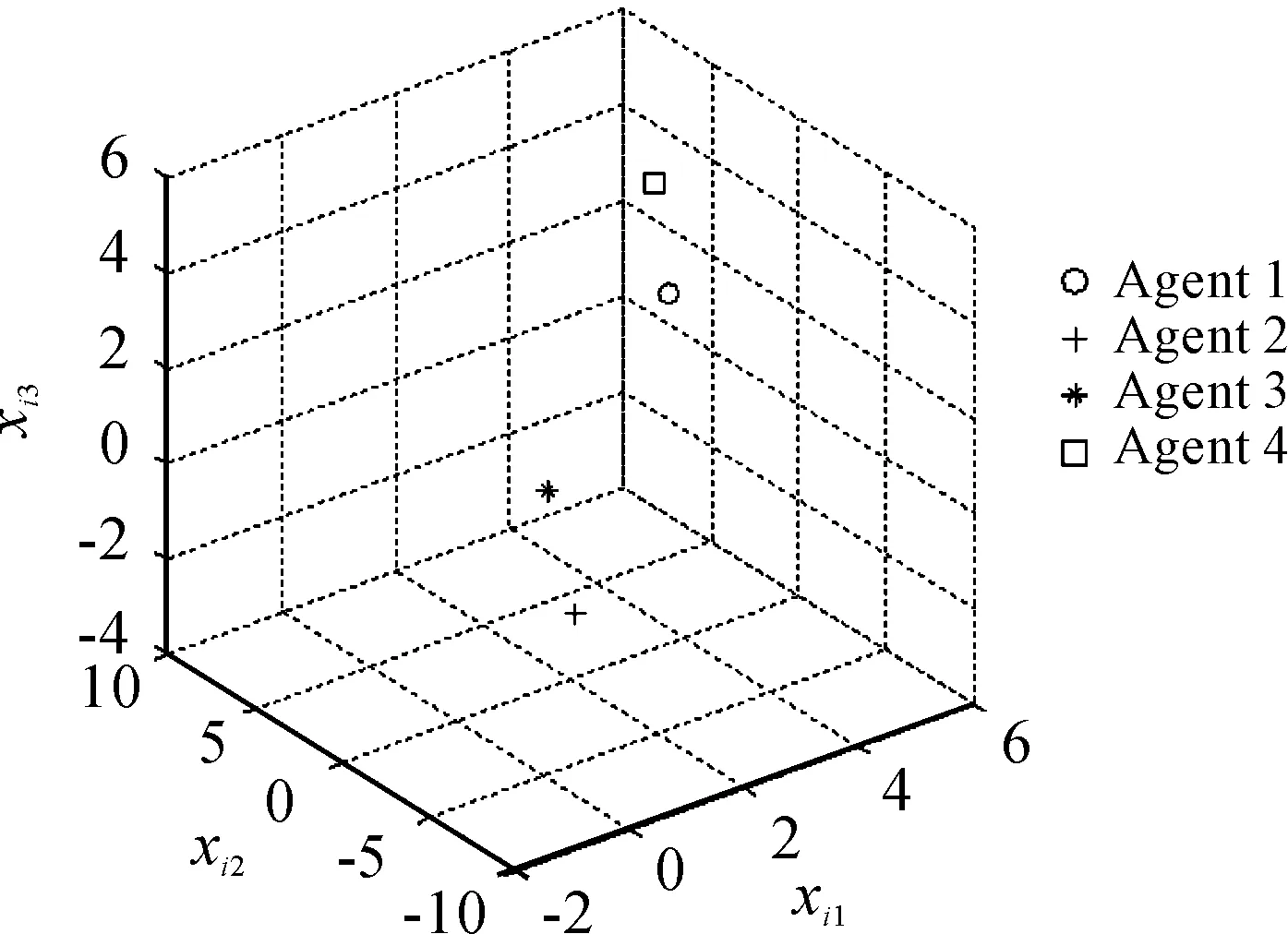
图4 t=5.5 s时编队队形

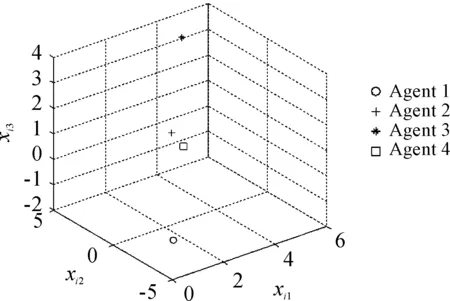
图5 t=20 s时编队队形

使4架无人机形成以上时变编队，使用的式 给出的基于事件触发的控制器，为了显示的清晰，将基于事件触发函数(17)设计的控制器触发时间间隔由图6表示，其表示0～10 s内的触发时间间隔，图6中横坐标为事件触发时刻，纵坐标为两次事件触发时间间隔。

从图6的事件驱动时间间隔看出，两次事件触发最小间隔为0.007 9 s，最大的时间间隔为0.197 s，平均时间间隔为0.042 9 s。根据公式计算最小时间间隔为0.007 3 s，由此观之实际仿真当中最小触发时间间隔是大于所要求的最小时间间隔，所设计的控制器有效，平均时间间隔和最大时间间隔明显大于系统所要求的最小时间间隔。

因此基于事件驱动下设计的一致性控制器能够使得系统形成时变编队，并有效降低智能体之间的通信压力。

图6 t=0-10 s内事件触发事件间隔tk+1-tk

5 结论

1) 本研究基于事件触发设计的分布式控制器，使得多智能体系统在事件触发时刻，进行通讯，两次事件触发时间间隔内无线通信保持休眠，节约了资源，减少了连续通信对系统造成的负担。

2) 所研究的拓扑结构为一般的有向拓扑，通过对Laplacian矩阵的特殊分解，将编队控制问题转为稳定性问题分析，降低了编队控制的难度，同时降低了通信要求。