基于滤波器设计的水听器测量信号幅度修正方法
黄聪,朱伟锋,王晓熔
中国舰船研究设计中心,湖北武汉430064
0 引 言
水听器可以将水下声信号转化为电信号,是水声学中不可或缺的测量传感器。水听器的接收灵敏度表示水听器接收声压与输出电压的转换比例,由于制作工艺的限制,水听器对不同频率信号的敏感程度存在一定差异,即水听器在不同频点上的灵敏度存在起伏[1-4]。
目前,声学采集设备一般通过设置固定的参考灵敏度进行声电转换计算。当接收单频信号时,可以通过计算水听器在该频点的实际灵敏度与参考灵敏度的差值,直接将测量信号乘以相应的幅度修正系数。当接收水下宽带信号时,由于水听器在不同频点上的灵敏度与参考灵敏度存在差异,将导致测量信号与实际信号出现偏差,所以需要根据水听器的灵敏度曲线进行幅度修正。由于宽带信号包含多个频点,且每个频点的修正幅度不同,所以无法直接利用单频信号的修正方法。目前,主要基于快速傅里叶变换(Fast Fourier Transform,FFT)的频域处理方法进行宽带信号修正,即把每个频点的频域信息乘以修正系数,再进行反傅里叶变换(Inverse Fast Fourier Transform,IFFT),从而得到时域信号。由于傅里叶变换是一种分块处理方法,需要一定的时间积累[5-6],所以实时性不足;同时,经过反傅里叶变换之后,各分块的时域信号不连续,将导致相位信息发生畸变,故需通过滑窗的方式替换分块连接处的失真数据,这将增加系统的运算量和复杂程度。
为了克服傅里叶变换分块处理的时间积累缺点,本文拟提出一种基于滤波器设计的水听器测量信号幅度修正方法,通过有限长单位冲激响应(Finite Impulse Response,FIR)滤波器对测量信号进行时域滤波,即可获取准确连续的水下声信号。该方法具备实时性好、相对误差小、运算量低等优点,可为水听器测量信号的幅度修正提供参考。
1 水听器各频点的灵敏度起伏
本文以B&K8105 型标准水听器作为水下声信号的接收设备,标准水听器的技术规格书中通常仅给出了部分频点的灵敏度值,如图1 中的离散点圈所示。本文将灵敏度值按照一定的频率间隔进行插值,即可得到更为详细的灵敏度曲线,如图1 中的插值曲线所示。由插值后的灵敏度曲线可知,整个接收带宽内的水听器灵敏度起伏在10 dB 以上。

图1 水听器的灵敏度曲线Fig.1 Sensitivity curve of hydrophone
假设实际的声学信号为s(n),信号形式为线性调频(Linear Frequency Modulation,LFM),频带为10~150 kHz,长度为50 ms。利用水听器进行接收时,设定采集器的参考灵敏度为-209.4 dB,采样频率为400 kHz。假设采集的测量信号为r(n),其时域波形如图2 所示。由于水听器各频点的实际灵敏度与参考灵敏度存在差异,这将导致测量得到的宽带信号与实际信号存在偏差,所以需要进行幅度修正。

图2 实际信号和测量信号的对比Fig.2 Comparison between actual and measured signals
2 基于傅里叶变换的幅度修正
基于傅里叶变换的幅度修正即是对测量信号进行时频转换,将每个频点的频域信号乘以修正系数,再进行反傅里叶变换,即可得到时域信号,具体步骤如下。
首先,将采集设备设定的参考灵敏度值M̂ 与水听器的灵敏度曲线M(fk)相减,计算各频点需要修正的幅度值A(fk),计算公式为

式中:fk为测量信号带宽的离散化频点,其中k=1,2,…,K,为频点数量;F 为水听器的接收频段。
然后,对测量信号r(n)进行时域分块,每块信号ri(n)的长度均为N 个采样点,再进行傅里叶变换,即可得到频域信号Ri(f)。其中i=1,2,…,I,为时域分块的数量。分别对每个频点的信号进行幅度修正,即可得到修正后的频域信号͂(fk)。


对图2 中的测量信号进行幅度修正,设定分块信号的长度为1 024 个采样点,修正后的时域信号和误差如图3 所示。可以看出,进行幅度修正之后,各分块在信号的起始端和末端出现了较大偏差,导致了拼接处的信号失真,故无法获得连续的时域信号。究其原因,经过离散傅里叶变换得到的频域信号Ri(f)是在频域采样的离散序列,对其进行幅度修正,就相当于在有限个离散频点上进行A(fk)的加权,这等效于在频域上加载不同幅度的矩形窗。当进行反傅里叶变换到时域之后,就相当于进行了带通滤波,故将导致时域信号r͂(n)在起始端和末端出现相位畸变。
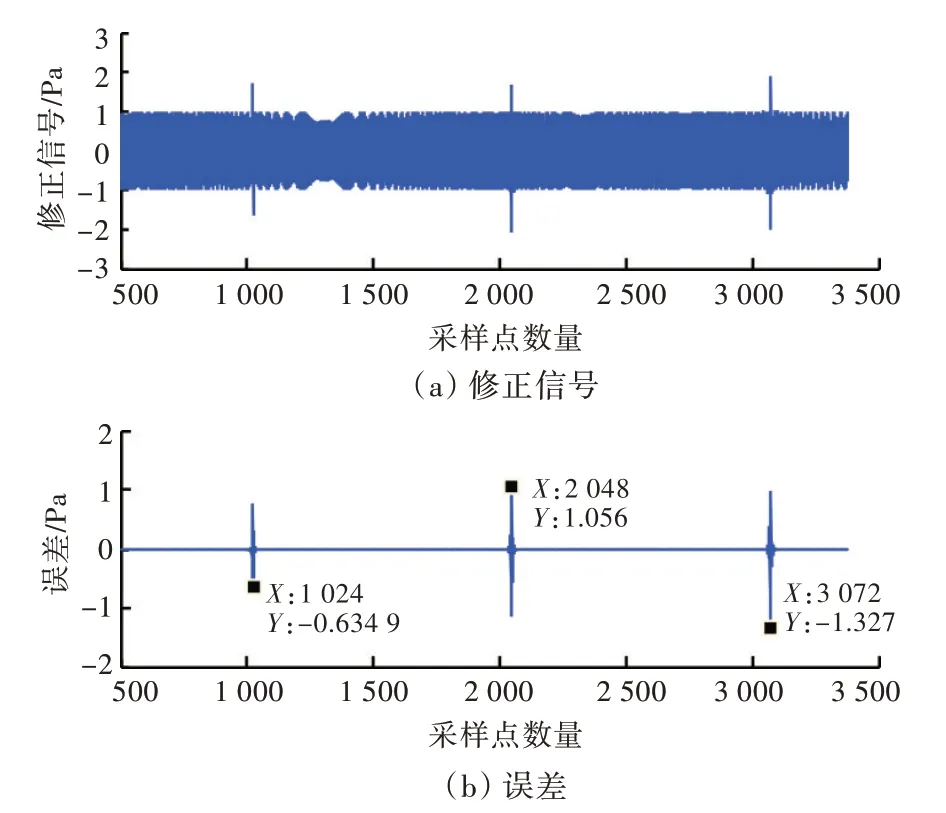
图3 基于傅里叶变换的修正信号Fig.3 Amplitude correction based on FFT
为了克服修正信号在分块连接处的畸变缺陷,可以通过重叠滑窗[7-8]的方式替换畸变信号,如图4 和图5 所示。对测量信号进行N/2 个采样点的重叠滑窗:第1 组为测量信号r(n),作为奇数分块;第2 组为除去前N/2 个采样点的测量信号rd(n) ,作为偶数分块。基于傅里叶变换进行幅度修正,得到的修正信号分别为r͂(n)和r͂d(n);分别截取每个分块的中间信号进行拼接,即可得到替换后的信号。

图5 滑动窗分块方式的流程图Fig.5 Flow chart of blocked mode by sliding window
利用重叠滑窗的方式,对图2 中的测量信号进行幅度修正,结果如图6 所示。由图可知,通过重叠滑窗可以替换分块连接处的畸变信号,且修正信号与实际信号的相对误差为0.5%。然而,该方法的本质仍然是基于傅里叶变换的分块处理,需要一定时间的积累,所以无法获取真正连续的时域信号,同时重叠滑窗将增加系统的运算量和复杂程度。

图6 滑动窗分块方式的修正信号Fig.6 Correction signal based on blocked mode by sliding window
3 基于滤波器设计的幅度修正
3.1 水听器灵敏度的滤波特性
由于水听器各频点的接收灵敏度存在起伏,所以水听器测量得到的声学信号已经对实际信号进行了滤波处理,滤波器的幅频特性即为水听器的灵敏度曲线。为了获取准确连续的时域信号,需要在保证相位不变的基础上对测量信号进行幅度修正。
鉴于FIR 滤波器良好的线性相位[9-10](图7),可以考虑将水听器的灵敏度修正转换为FIR 滤波器的设计问题。图7 中:T1为信号延迟;Ts为采样延迟;h =[h1,h2,…,hL],为滤波器系数,其中L 为滤波器的长度(无量纲)。本文将每个频点需要修正的幅度值A(fk)作为期望的幅频响应,通过设计满足幅频特性的FIR 滤波器,对测量信号r(n)进行时域滤波,从而获取连续的时域修正信号r͂(n)。

图7 FIR 滤波器示意图Fig.7 Sketch of the FIR filter
3.2 FIR 滤波器设计
假设FIR 滤波器系数为h,长度L=2x+1,其中x 为整数。滤波器的长度越长,设计精度就越高,但其时延将越长,运算量也越大,可以根据实际精度需求来调整滤波器的长度。假设测量信号的采样率为fs,延迟Ts=1/fs,则FIR 滤波器的频率响应H(fk)为

式中,[0:L-1]=[0,1,…,L-1],为横向量。
将幅度修正值A(fk)作为期望的幅频响应,由于FIR 滤波器存在(L-1)/2 个采样点的群时延,则FIR 滤波器期望的频率响应Hd(fk)为

将设计频率响应H(fk) 逼近期望频率响应Hd(fk),其准则为约束信号带宽内所有设计频点的误差总和ξk最小,即

式中:fk∈FPB和fm∈FSB分别为关注频段和非关注频段的离散频点,其中FPB为关注频段,FSB为非关注频段,m=1,2,…,K,为频点数量;λ(fk)和λ(fm)均为各离散频点的加权系数;Hd(fm)为非关注频段的期望频率响应;γm为非关注频段幅频响应的最大值上限。
本文将利用二阶锥规划方法[11-13]对式(7)的约束条件进行解算,设计出满足期望频率响应的FIR 滤波器,再通过时域滤波实现测量信号的幅度修正,其流程如图8 所示。
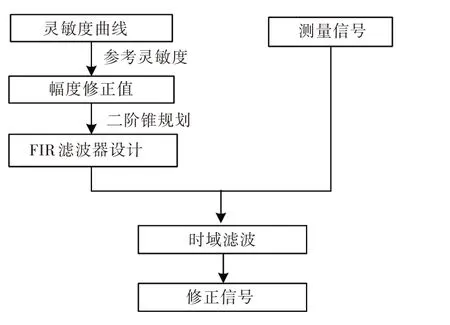
图8 基于滤波器设计的幅度修正流程图Fig.8 Flow chart of amplitude correction based on FIR filter design
3.3 仿真分析
本文设计的滤波器长度L=513,采样频率fs=400 kHz,关注频段为1 Hz~160 kHz,非关注频段为160~200 kHz。利用二阶锥规划方法设计FIR 滤波器的系数,其幅度频率响应和相位频率响应分别如图9 和图10 所示。

图9 幅度频率响应Fig.9 Amplitude-frequency response

图10 相位频率响应Fig.10 Phase-frequency response
采用该FIR 滤波器对水听器测量的LFM 信号和宽带噪声进行时域滤波,修正后的信号和误差如图11 和图12 所示。由处理结果可知,通过FIR滤波器对测量信号进行时域滤波之后,可以获取真正连续的修正信号。

图11 基于滤波器设计的LFM 信号修正Fig.11 LFM signal correction based on FIR filter design

图12 基于滤波器设计的宽带噪声修正Fig.12 Wide-band noise correction based on FIR filter design
LFM 信号和宽带噪声经过幅度修正之后,其相对误差随滤波器长度的变化曲线如图13 所示。由处理结果可知,修正信号的相对误差随滤波器长度的增加而减小:当滤波器长度为129 时,修正信号的相对误差为0.4%;当滤波器长度为257 时,修正信号的相对误差仅0.3%。
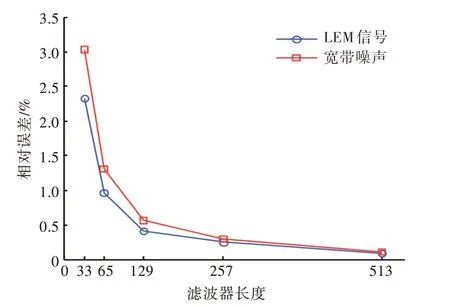
图13 相对误差随滤波器长度变化曲线Fig.13 Variation of relative error with respect to the length of filter
4 结 语
本文提出了一种基于滤波器设计的水听器测量信号幅度修正方法,可以将测量信号的幅度修正问题转化为FIR 滤波器的设计问题。通过设计出满足幅频特性的滤波器系数,再对测量信号进行时域滤波,即可得到准确连续的宽带修正信号。该方法仅需对测量信号进行时域滤波,从而克服了傅里叶变换分块处理需要时间积累的缺点,在确保获取准确修正信号的同时,也保证了良好的实时性。

