水轮发电机组抑制超低频振荡的阻尼控制参数优化研究

周鑫，和鹏，何鑫

(云南电网有限责任公司电力科学研究院，昆明 650217 )

0 前言

云南电网与南方电网鲁西背靠背直流异步联网工程常规直流单元建成，实现了首个省级电网与大区域电网实现异步互联。为测试异步联网系统的稳定运行能力，开展了云南异步联网系统性整体实验。在第一次试验中，云南电网出现了长时间、大幅度的超低频现象，范围在49.9 ～50.1Hz 之间，振荡周期约为20s。在退出小湾、糯扎渡等水利电厂的一次调频后，系统频率恢复正常[1-2]。研究表明超低频振荡主要由于大量的水电机组的水锤效应和调速系统引起的负阻尼所致。调整水电机组调速器PID参数和控制调速器死区可以有效抑制超低频振荡[3]。

已有研究表明在直流孤岛运行方式下，也存在类似超低频振荡的现象。文献[4]针对锦苏直流送端孤岛中的超低频振荡问题，建立了基于直流孤岛系统的调速器分析模型，从频域的角度研究调速器稳定性的影响因素。文献[5]通过特征根和时域仿真的方法对孤岛系统中的超低频振荡进行了分析和排查，表明了超低频振荡是由于孤岛中调速系统引起的机械振荡模式。文献[6-7]分别从单机系统和多机系统分析了振荡频率、阻尼等关键因素，采用相量图的方法说明了超低频振荡的功率更多表现为机械振荡，并且提出了一种适用于超低频振荡分析的将多机系统等值为单机系统的等值方法，研究分析了多机系统中各发电机的阻尼特性。文献[8-11]指出特高压直流送出系统的运行控制是极其复杂的，在系统由联网转孤网运行时，容易出现频率振荡等一系列问题，其中调速系统对于孤网的稳定性有着十分重要的影响。文献[12-13]针对哥伦比亚电网中出现的超低频振荡现象，利用动力学建立了水力耦合发电装置的动态模型及其多单元的频率稳定性研究，采用建模和时域仿真的方法分析了系统控制器和水轮机对于系统频率振荡的影响。预计在2020 年我国将有超过10 个特高压直流孤岛系统，但与联网运行相比，孤岛方式存在暂态稳定的风险，所以对直流孤岛系统中出现的频率波动异常情况应予以高度的重视。

本文在以往研究的基础上，利用PSD-BPA软件对云南电网的实际孤岛进行研究，根据系统阻尼比变化分析了水锤效应与系统稳定性的关系。基于系统调速系统的阻尼特性，提出了优化PID 参数的方法。接着，研究了一次调频对于系统频率和直流功率的影响，提出一次调频与直流频率控制器的协调控制方法，最后，通过云南电网的某实际直流孤岛的仿真算例，验证了本文控制方法的有效性。

1 直流孤岛系统

1.1 水电站N直流孤岛的振荡问题

水电站N 位于云南省， 直流电压为±800 kV，直流输电容量可达到5000 MW。水电站N 规划了9 台机组发电，均为水轮机，单机最大出力650 MW，水电站N 和换流站A 通过3 回525 kV 线路直流送电，再通过换流站A-地区B 双回线与云南电网联络。当断开换流站A-地区B 双回线后，也就切断了这一地区与云南电网主网的联系，形成了直流孤岛，如图1 所示。

在水电站N 直流孤岛形成后，6 台发电机正常运行，3 台发电机作为备用容量。每台发电机出力为650 MW。在发生初始扰动后，系统频率出现异常波动，波动周期约为20 s，波动幅度约为49.80 ～50.28 Hz，且6 台机组同相波动，频率低于正常机电振荡频率范围(0.1 ～2 Hz)，属于超低频振荡现象。如图2 所示。

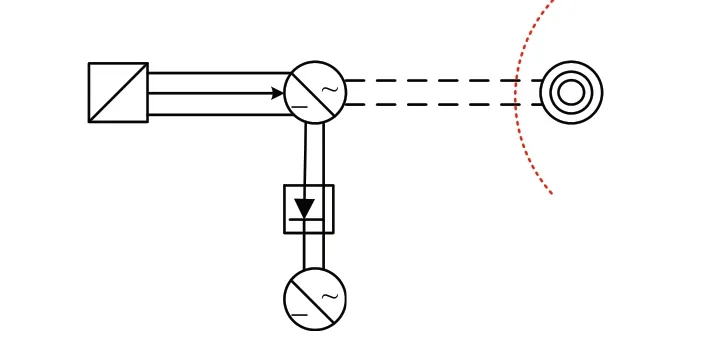
图1 水电站N地理接线图

图2 水电站N的频率异常波动情况

1.2 发电机及直流频率控制器模型

水电厂N 的发电机组均为水轮机，故本文也主要讨论水轮机模型。所用的发电机模型为平衡点附近的线性化模型。由发电机的转子运动方程可知，发电机转速受机械功率和电磁功率共同作用，即：

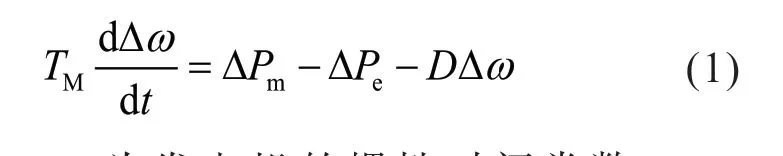
式中：TM 为发电机的惯性时间常数，Pm为原动机机械功率输出偏差，Pe为电磁功率偏差，D为发电机阻尼系数。

若忽略网损和电压变化，发电机的电磁功率变化等于负荷有功变化量和直流输送功率变化量的和。当直流频率控制器（FLC）不投入使用时，直流功率不受频率变化影响，则Pe=KL，其中KL为负荷频率调节效应系数，发电机传递函数可写成：

式中，Ds=D+KL。

当直流频率控制器投入运行时，相当于为直流增加了频率特性，本文所用的直流频率控制器模型如图3 所示。若只考虑直流频率控制器模型的比例积分环节，发电机传递函数简化表示为：

式中：D's=D+KL+KHP，KHP为比例环节系数，KHI为积分环节系数。

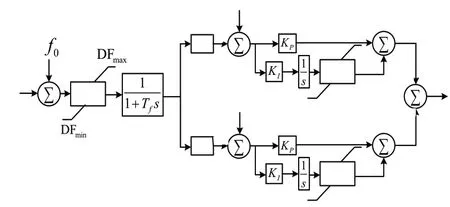
图3 直流频率控制器模型

图4 中给出了FLC 在不投入和投入运行状态时的发电机及外部系统的伯德图对比。可以看出，在直流频率控制器投入运行之后，幅频曲线下移，相频曲线上移，主要影响了0.001～1 Hz 频段的频率响应特性。在幅值响应上，降低了低频率段的幅值增益，相当于加大了幅值裕度；在相频响应上，减小了低频率段的相位滞后，也就是提高了相位裕度。直流频率控制器对于直流功率能够快速调整，在实际系统中可充分发挥稳定的调节特性，与调速系统的一次调频共同抑制系统频率振动，因此，在研究直流孤岛中出现的超低频振荡现象时，需要考虑FLC 对于频率稳定的影响。

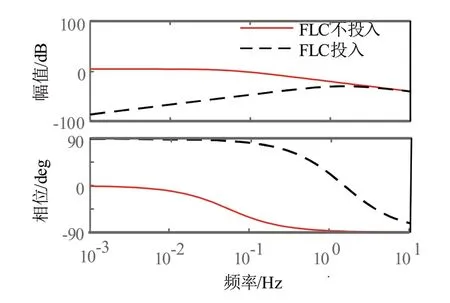
图4 FLC对系统频率响应的影响

2 水锤效应及系统稳定性分析

2.1 水轮机及调速器数学模型

水轮机模型是水轮机导水叶开度和输出机械功率Pm 之间的动态关系。本文采用简化的水轮机及其引水管道动态模型，只考虑由于水流惯性引起的水锤效应，其传递函数为：

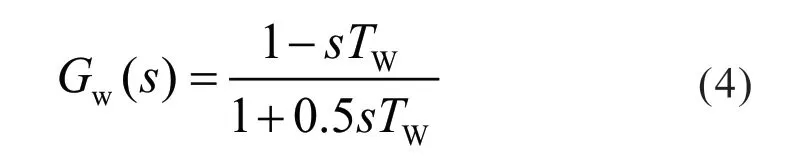
式中：TW 为水锤效应时间常数，在满载时一般取值为0.5 ～4.0 s。

在PSD-BPA 软件中水轮机调速系统主要采用电调型调速系统，由调节系统(控制系统)、电液伺服系统和原动机组成。调节系统模型采用PID 型调速器，其传递函数一般表示为

式中：KP、KI、KD 分别为调速器的比例、积分和微分系数，BP 为调差系数，TG 为执行机构时间常数。

2.2 单机系统稳定性分析

在上述发生的超低频振荡现象中，6 台机组同相波动，转速大小和相位都相同，所有的发电机的转速偏差都相同，因此可以对水电站N中的6 台发电机进行动态等值，所等值后的单机系统的传递函数框图如图5 所示，其中Δωref为转速偏差参考值。

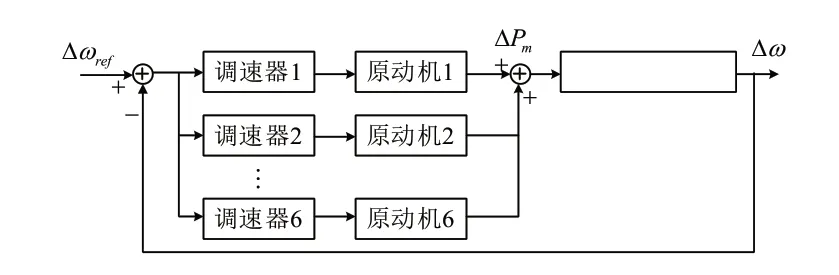
图5 系统等值模型

云南电网异步联网的第一次试验中，出现了超低频振荡现象，表明研究云南电网的水电机组的水锤效应提供的负阻尼是导致超低频振荡的原因之一。因此可以对水锤效应进行研究分析，考虑TW 对于系统的频率稳定的影响。在等值后的单机系统中，暂不考虑直流频率控制器的影响，系统的开环传递函数为：

根据自动控制理论知识可知，由系统的闭环极点也可以反映出系统的稳定性。在闭环极点中，存在一对复数特征根，其阻尼比可表示为：

当ξ＜0，该系统不稳定的；当ξ=0，该系统处于稳定边界；当ξ＞0，该系统是稳定的，ξ越大，该系统稳定阻尼越强。

根据等值后的单机系统开环传递函数，由系统的闭环极点可计算出系统阻尼比。图6 给出了系统阻尼

比随水锤效应时间常数变化的曲线，当TW＜2.06 时，阻尼比为正，说明系统稳定；TW＞2.06 时，阻尼比为负，系统不稳定。

图6 不同TW对阻尼比的影响

表1 是TW取值为2.06 ～2.20s时，系统特征值的变化情况,同时说明了随着TW增加，系统特征值实部变大，阻尼比不断减小，系统稳定性逐渐减弱。

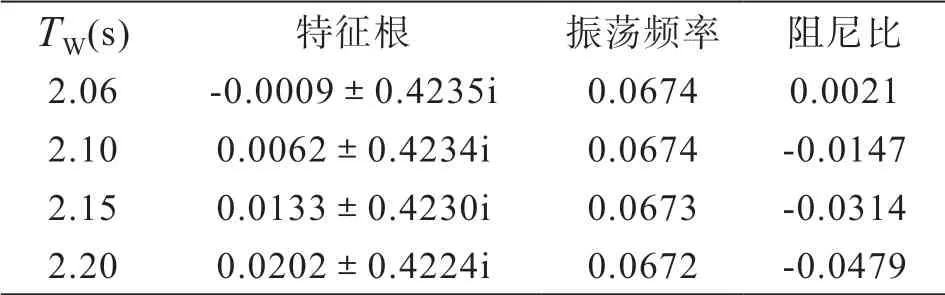
表1 水锤效应对特征值的影响

图6 和表1 中可以看出，在TW＞2.06s 后，阻尼比的曲线呈现负值，且系统特征值实部逐渐增加，阻尼比由正到负，不断减小，说明由水锤效应引起的负阻尼效应加剧，系统稳定性逐渐恶化。在孤岛系统中，系统稳定性对于TW更加敏感，频率变化与水锤效应更加密切，因此对于水轮机组的参数准确性要求更高。

3 直流孤岛调速系统阻尼分析

3.1 水轮机调速器阻尼特性分析

现对调速器模型进行简化，不考虑PID 参数，只考虑调差性能，原动机调节系统传递函数为：

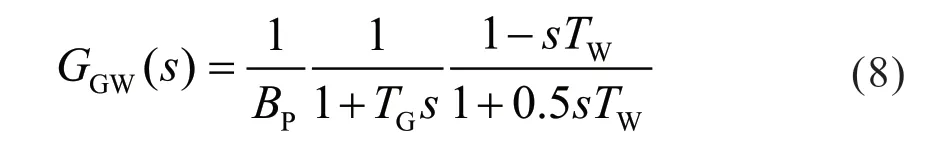
根据Phillips-Heffron 模型，原动机调速器产生的机械功率变化Pm 与转速偏差关系为：

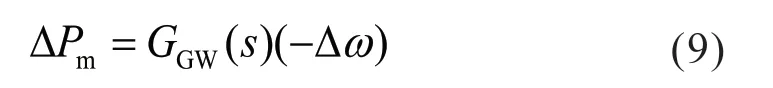
将s=jωd代入式（9）中，可得

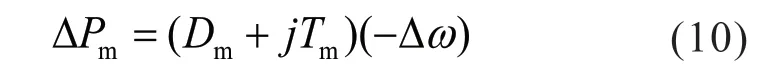
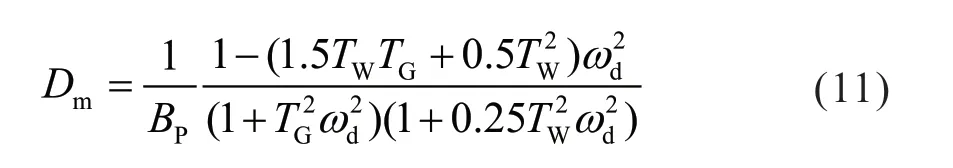
令Dm=0，可得

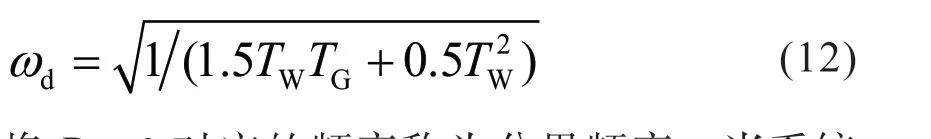
将Dm=0 对应的频率称为分界频率，当系统振荡频率高于分界频率，水轮机调速系统产生负阻尼；振荡频率低于分界频率，水轮机调速系统产生正阻尼。

由式(12) 计算可得，参数组1 的分界频率为0.061 Hz，参数组2 的分界频率为0.089 Hz，式(12)的计算结果与2 组参数下对应的分界频率一致。

3.2 调速器PID参数控制

现考虑调速系统的PID 参数，原动机调节系统传递函数为

将s=jωd代入式（13）可得

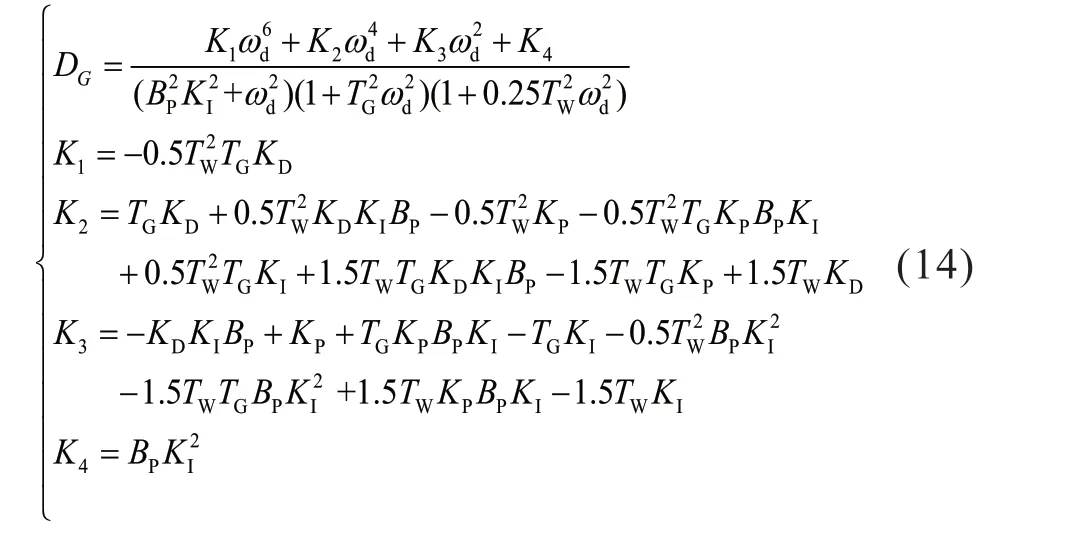
对调速器的控制参数进行阻尼转矩特性分析，在改变KP、KI、KD、BP 参数的情况下，分析水轮机调速器的阻尼转矩系数随频率变化情况，如图7 和8 所示。

图7 KP、KI对阻尼转矩系数的影响

图8 BP、KD对阻尼转矩系数的影响

图7 中，在0.01 ～0.1Hz 的超低频段，当KP 增大时，其阻尼逐渐减弱，甚至出现负阻尼；KI 在超低频段负阻尼特性显著，且KI 越大，负阻尼的幅值越大。图8 说明在超低频段，BP减小，阻尼略微减弱；KD 基本提供正阻尼。

以上分析表明水轮机的调速器控制参数的大小极易影响系统的阻尼特性，因此，为产生稳定的频率响应，改善系统阻尼，需要适当减小KP、KI 使调速系统呈现正阻尼特性，更有利于提高调速器稳定性。

在水电站N 直流孤岛进行仿真试验，调速器参数为：KP=3，KI=1，KD=1，BP=0.04。减小KP、KI 参数，孤岛系统频率变化如图9 所示。图中，在KP=3，KI=1 时，系统发生超低频振荡，原动机调速系统产生负阻尼转矩，水轮机调节系统提供负阻尼。KP=2，KI=0.2 时，系统为衰减振荡，原动机调速系统产生正阻尼转矩，水轮机调节系统提供正阻尼。KP=0.5，KI=0.02 时，系统振荡衰减，但相对于KP=2，KI=0.2 时振荡峰值明显更大，调速器响应时间更长。

图9 PI参数对系统频率的影响

根据原动机阻尼转矩特性调整调速器PID参数，仿真结果表明，减小KP、KI 参数，增加了调速系统所提供正阻尼，有利于抑制超低频振荡，这与图7 和图8 所得结论一致。但KP、KI 参数取值过小，会降低调速器响应速度，所以在实际系统中，需要根据实际情况协调调整才能产生比较理想的系统阻尼。

4 调速系统与直流FLC的协调控制

4.1 一次调频退出试验

在实际直流孤岛中，直流频率控制器比例环节KHP=30，积分环节KHI=22.2，死区DF=±0.2Hz，调速器死区DG=±0.05Hz。图4中给出了FLC 在不投入运行和投入运行状态时的频域响应，在直流孤岛中对FLC 投入运行和退出运行时的频率动态进行仿真，如图10 所示。

图10 有无FLC的系统频率动态变化

直流频率控制器退出之后，系统失稳，失去直流FLC 的作用后，一次调频对直流孤岛的频率恢复作用受限，导致孤岛系统频率大幅度振荡。在FLC 投入后，孤岛频率出现等幅振荡模式，其振荡幅值约为49.73 ～50.25Hz，频率振荡幅值超过0.2Hz，FLC 动作，在调速系统和FLC 的共同作用下，系统没有出现失稳现象，但存在小幅振荡。FLC 投入后，依次退出一次调频，孤岛频率变化如图11 所示。

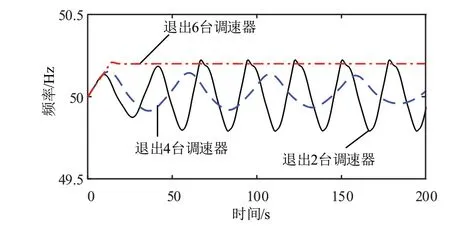
图11 退出一次调频孤岛频率变化图

图11 中，退出2 台调速器之后，孤岛频率为负阻尼振荡模式，最大振幅不超过50.2 Hz，相较于退出调速器之前的频率略有减弱。在退出4 台调速器之后，系统频率振荡幅值明显减小，最大幅值为50.17 Hz，且振荡处于衰减状态，负阻尼特性减弱，FLC 未参与调频。在退出6台调速器后，孤岛系统一次调频全部退出，系统频率基本稳定在50.2 Hz，机组频率仅在FLC作用下恢复稳定。

可以看出，退出调速器的数目越多，阻尼比越大，系统频率振荡衰减逐渐变大，系统逐渐稳定。由以上仿真和计算结果表明，孤岛系统内所有机组均参与超低频振荡，水电机组调速系统提供振荡的负阻尼，且参与机组的调速器越多，提供的负阻尼越大，其超低频振荡现象越显著。

4.2 直流FLC与一次调频配合控制

1）直流FLC 死区的影响

在不退出调速系统的情况下，调速器的死 区DG 为±0.05 Hz， 直 流FLC 的 比 例 环节KHI=22.2，积分环节KHP=30。改变直流频率控制器死区DF，分别取为±0.02 Hz 和±0.1 Hz。

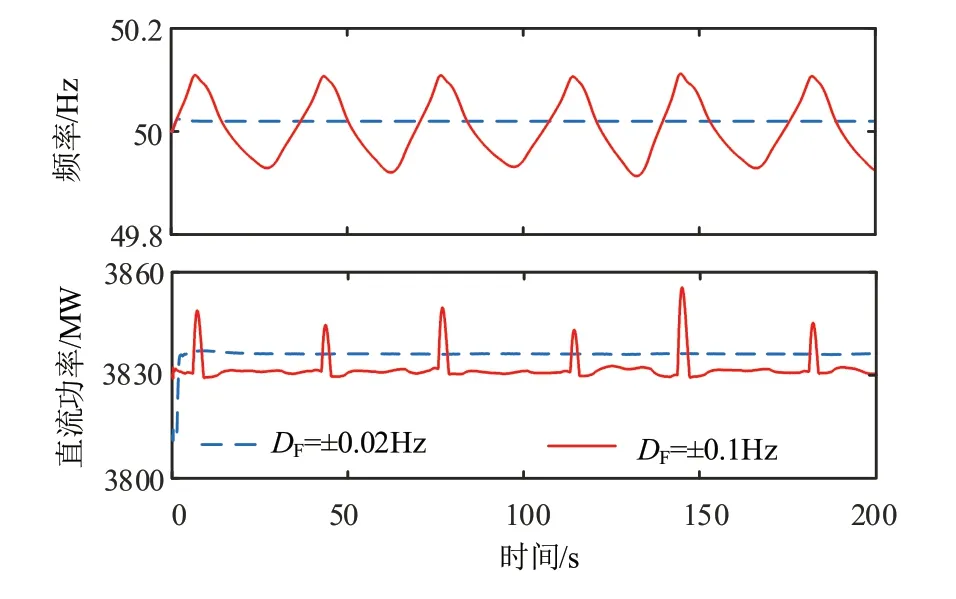
图12 不同FLC死区的影响

图12 中， 当DF=±0.1 Hz 时， 相 对 于DF=±0.2 Hz( 图2) 时的频率波动幅度明显减弱。调速器产生的负阻尼效应依然存在，由于FLC 的限制，系统发生小幅度的振荡。当DF=±0.02 Hz 时，FLC 死区小于调速器的死区，导致FLC 先于调速器动作，系统频率在调速器动作之前由于FLC 作用已经恢复稳定，频率振荡幅值不超过50.03 Hz，而调速系统所提供的负阻尼振荡失去作用，从而达到抑制超低频振荡的目的。

2）直流FLC 的PI 参数控制

对于直流频率控制器的积分环节，在与云南电网联网实际运行时，由于系统惯性很大，FLC 在进行快速无差调节时可能导致直流功率频繁快速大范围的动作。一般将KHI 置于零或较小数值，因此本文不作讨论，下面对比例系数KHP 进行仿真分析。

水 电 站N 直 流 孤 岛 中，KHI=22.2，DF=±0.02Hz，DG=±0.05Hz，取KHP 分别为30 和100，其频率变化如图13 所示。KHP 变大时系统频率的波动峰值明显下降，且频率振荡幅度减弱，有功功率的变化趋势与孤岛频率的变化一致，说明KHP 变大时更有利于抑制超低频振荡现象。

通过上述试验，基于调速系统与直流FLC的协调控制，为抑制直流孤岛中的超低频振荡现象，建议放大调速系统的动作死区，减小直流频率控制器的死区，DG＞DF 时可充分发挥FLC 的调节作用，有利于调速器稳定性。且应增大FLC 的比例系数KHP，使得直流FLC 在频率波动中尽量为线性调节；减小积分系数KHI，将KHI 置于零或较小数值，避免直流功率频繁快速的大范围调节。

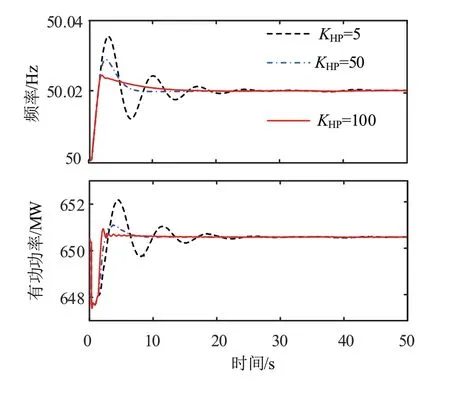
图13 不同比例系数KHP孤岛频率变化

5 结束语

实际直流孤岛中，发生初始扰动后出现超低频振荡现象。本文对这一现象进行了分析，得出结论如下：

1）基于频域响应分析了直流FLC 在孤岛中的影响，投入直流FLC 后有利于提高系统稳定性。

2）在等值单机系统中探讨了水锤效应时间常数对于系统稳定性的影响。当TW=2.06s 时，系统处于临界阻尼状态，TW＞2.06s 后系统稳定性有所下降。

3）通过调速系统的阻尼转矩分析表明，适当减小KP、KI 参数有利于抑制超低频振荡，孤岛仿真中KP=2，KI=0.2 时系统调速器提供正阻尼，系统频率逐渐稳定。

4）对一次调频与直流频率控制器的协调控制进行了仿真研究，结果表明减小直流FLC 的动作死区，增加直流频率控制器的比例系数，能够有效地抑制超低频振荡现象。