基于策略式博弈的云南日前电量市场分析

邢玉辉，张茂林，刘双全，周娜，马高权，刘祥瑞，谢蒙飞，和珮珊

（昆明电力交易中心有限责任公司，昆明650011）

0 前言

云南率先建立全国第一个省级日前电量市场[1-5]，本文从博弈论的角度，对该市场的运行情况进行了分析，对其他省份设计日前电量市场机制具有一定的参考和借鉴意义。

日前电量交易是指竞争性售电主体与竞争性用户之间进行次日发用电量交易的品种，是中长期交易的一种延伸和补充。

博弈论是专门研究2 个或2 个以上利益有冲突的个体，在有相互作用的情况下，如何进行各自优化决策的理论[6-8]。

在电力市场中，各市场主体在规则允许的条件，根据已知信息，如何制定有效的交易策略进行合理竞争获取最大利益，就是一个典型的博弈问题。交易双方相互试探、报价直至成交的过程，也是一个交易双方根据市场形势相互博弈的过程。

运用博弈论分析电力市场，有助于市场参与者更好地制定有利于自身的交易策略，有助于市场运营者更好地理解市场参与者的交易行为[9]。

1 博弈论基础

策略式博弈又称标准式博弈，许多博弈理论者将参与人的策略当作模型的首要因素。策略式博弈由三种元素组成：参与人集合、每个人的纯策略空间以及收益函数，并给定每种策略所产生的效用。在这些元素的函数关系中，每个人的目标是最大化自身的收益[10-11]。

纳什均衡是指博弈中这样的局面，对于每个参与者来说，只要其他人不改变策略，他就无法改善自己的状况。纳什证明了在每个参与者都只有有限种策略选择并允许混合策略的前提下，纳什均衡定存在。以两家公司的价格大战为例，价格大战存在着两败俱伤的可能，在对方不改变价格的条件下既不能提价，否则会进一步丧失市场；也不能降价，因为会出现赔本甩卖。于是两家公司可以改变原先的利益格局，通过谈判寻求新的利益评估分摊方案。相互作用的经济主体假定其他主体所选择的战略为既定时，选择自己的最优战略的状态，也就是纳什均衡[12]。

2 简化的双人博弈模型

对日前电量市场中的模型进行简化，先简化至最简单的双人博弈模型。假设日前电量市场中仅有一家小型电厂A 和一个用户B。根据云南电力市场的装机特性，假设参与日前交易的全部为水电，电厂的发电成本为FC 为一常数，与发电量无关，忽略水资源费等假设其边际成本为0。假设用户的用电需求为qB，其需求曲线为刚性。电厂A 的发电量为qA。假设用户的用电量与电厂的发电量相等，记为q：

电厂电厂A 的申报价格为pA，用户B 的申报价格为pB，双方的申报电量均为q。

按照《2017 年云南电力市场化交易实施方案》中日前电量市场的成交和结算规则，成交情况如下：

（1）电厂电厂报价不高于用户报价，即pA≤pB时，电厂和用户全部电量成交，成交量均为q。

电厂电厂A 的成交价格为：

用户B 的成交价格为：

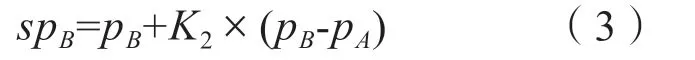
电厂电厂A 的发电收益为：

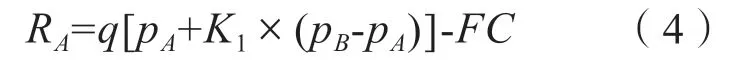
用户的购电成本为：

（2）电厂电厂报价高于用户报价，即pA＞pB时，电厂和用户均不成交，成交电量为0。

此时电厂电厂A 的发电量均为未成交超发电量，结算价格为预招标上调服务报价，记为pG；用户B 的用电量均为未成交超用电量，结算价格pU，其中pG＜pU。

电厂电厂A 的目标是发电收益RA最大化：

用户B 的目标是购电成本RB最小化：

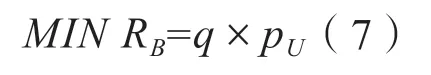
容易看出， 用户的报价pA必然不高于pU， 电 厂 的 报 价 必 然 不 低 于pG， 故有不 难 得 到， 满 足的都是这个双人博弈的纳什均衡解。实际市场中，因为申报电价的梯度G 的限制，区间[pG,pU]中可申报电价是有限的，可申报电价的集合记为P，其元素为pi，i=1,2,...N，其中pj＜pk(j＜k)。故这是一个有限博弈，其纳什均衡解的数量是有限的。

每月的日前电量市场都是当月每天开展一次的重复博弈。很自然地，在这个重复博弈中，电厂电厂A 可采取的一种保守的策略是“试探法”，即第一天申报价格定为p1，若成交且成交价但与申报价不相同，说明电厂电厂A 与用户B 的报价仍然有价差存在，为追求发电收益最大化，电厂电厂在次日将报价上调G；若成交且成交价与申报价相同，说明已经达到纳什均衡解，则维持该报价直到当月结束；若未能成交，说明报价过高，则在次日将报价下调G。同样地，用户B 也采取类似的“试探法”，即第一天将申报价格定为pN，若成交且成交价但与申报价不相同，说明电厂电厂A 与用户B 的报价仍然有价差存在，为追求购电成本最小化，用户在次日将报价下调G；若成交且成交价与申报价相同，说明已经达到纳什均衡解，则维持该报价直到当月结束；若未能成交，说明报价过低，则在次日将报价上调（若已经是 则不再上调）。若电厂电厂A 和用户B都采取上述的“试探法”，那么在市场的自由博弈中有50%的概率能够达到纳什均衡解，另外50%的概率无法达到纳什均衡解而是在两个解和直接来回摆动，其中

此时我们再假设另一种情形下，电厂电厂A 而采取“强硬”的报价策略，而用户依然采取“试探法”，即在月初确定一个报价cpA，该价格全月都保持不变。用户则继续采取上述的“试探法”。那么市场必将达到纳什均衡，均衡点为pA=pB=cpA。如果电厂电厂A 预测到用户会理性地采用“试探法”，那么从发电收益最大化的考虑，电厂电厂A 在月初制定cpA时，就会倾向于制定更高的cpA。

实例分析：为了便于分析，将实际的日交易市场作适度的简化，假设pG=0.23 元/kWh，pU=0.26 元/kWh，G=0.01 元/kWh，N=4，q=1000kWh， 则 可 申 报 电 价 集 合 为{p1=,p2,p3,p4}。电厂A 和用户B 均采取“试探法”，电厂A 的初始报价pA0=p1=0.23/kWh，Y 用户B的初始报价pB0=p4=0.26/kWh。将电厂电厂A 和用户B 博弈的策略式展现为矩阵，矩阵的每个单元格中展示的是电厂电厂和用户的收益（电厂电厂收益为发电收入，用户收益为负的购电成本），电厂电厂和用户都会朝着使自身收益更大的方向移动。则最终市场将在(0.24,.025)和(0.25,0.24)间来回摆动。

表1 用户B报价

此时若电厂电厂A 改为“强硬”的报价策略，而用户保持“试探法”策略不变。假设电厂电厂A 的初始报价pA0=0.26/kWh，用户B 的初始报价为pB0，则不论pB0取何值，用户B 在收益的驱动下都会向pA0靠近，最终在市场价格停留在(0.26,0.26)。

表2 用户B报价

3 考虑发电联盟的三人博弈模型

3.1 售电主体建模

以2017 年3 月的市场为例，给出3 月1 日的售电电价申报汇总信息，如表3 所示。

由表3 可以看出，申报价格在0.245 元/kWh 的电量非常大，这个电量远超日前电量交易中所有用户的需求，该电量主要由日前电量市场中的几个大型电厂以同一价格申报。这几个电厂的发电能力都很大，甚至单独一个电厂即可满足日前交易中所有用户的需求。这些大型电厂均属于国有大型发电集团，可认为其在市场中组成了大型发电联盟，约定了统一的申报价格[14-15]。

申报价格在0.245 元/kWh 以下的电厂则大多发电能力较小，且不属于国有大型发电集团，单独行动不与其他电厂合作。

申报价格在0.245 元/kWh 以上的电厂完全没有成交机会，这些电厂大多是抱着试试看的心态，对市场最终成交没有任何影响，在建模时暂时先不予考虑。

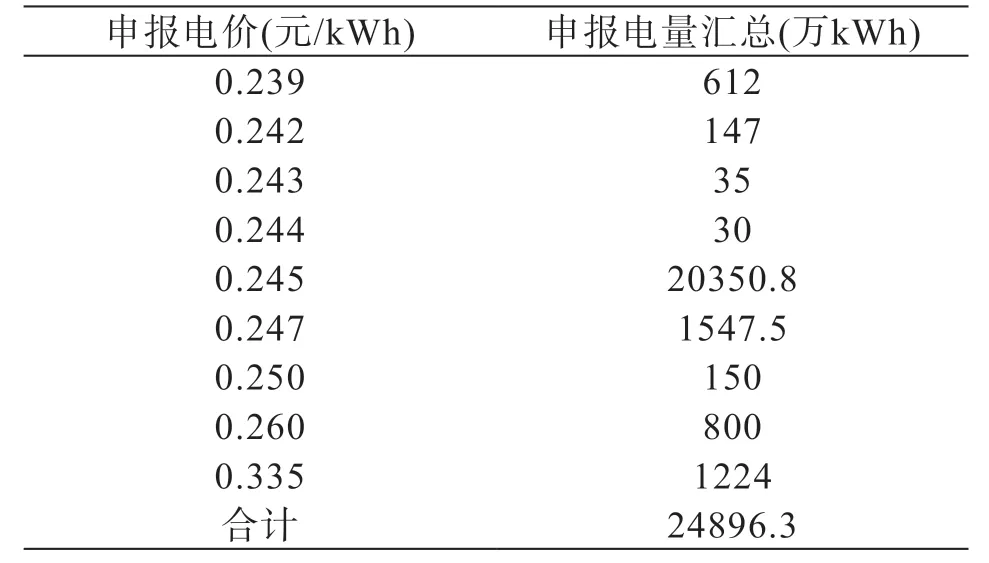
表3 3月1日的售电电价申报汇总表

根据上述分析，可以对售电主体建模：设有大型发电联盟C，其采取“强硬”的报价策略，每月固定一个申报价格pC，申报电量为qC。设有一家小型电厂A 申报价格分别为pA，每天发电量为qA。报价方法采取上述的“试探法”。小型发电厂事先已经知道大型发电集团联盟的报价，但为了抢到电量，小型电厂的报价低于大型发电集团联盟的报价，即有pA＜pC。大型发电集团联盟的发电量远远大于小型电厂的发电量，即有qA＞qC；小型发电厂和大型发电集团联盟的发电量足够满足用户B 的用电需求，即有qB≤qA+qC。

3.2 购电主体建模

目前，日前电量市场中的购电主体非常分散，可以假设购电主体均为单独行动不与其他用户合作，不可能形成用户联盟而采取“强硬”的报价策略。设有用户B，申报价格分别为，每天用电量为qB。报价方法采取上述的“试探法”。

3.3 三人博弈模型

实例分析：为了便于分析，将实际的日交易市场作适度的简化。假设PG=0.23 元/kWh，PU=0.26 元/kWh，G=0.01 元/kWh，N=4， 则可申报电价集合为{p1=,p2,p3,p4}。小型电厂A的初始报价pA0=p1=0.23 元/kWh，Y 用户B 的初始报价pB0=p4=0.26 元/kWh。大型发电集团联盟C 的报价pC=0.25 元/kWh 保持不变。设qA=1000kWh，qC=105kWh 对于，对于qB分为不同情况来讨论其策略式博弈。

1)qB＜qA，举例qB=qA=1000，容易看出，此情形下，因为pA＜pC，根据撮合成交的规则用户B 全部与小型电厂A 成交，故其博弈的策略式可以展现为图X 所示。

表4 用户B报价

由矩阵分析可以得到，市场最终将在(0.24，0.24，0.25)处达到纳什均衡。

2)qA＜qB≤qC，例如qB=qA=2000，容易看出，此情形下，小型电厂A 的全部发电量仍然不能满足用户B 的需求，大型发电联盟C 参与到与用户B 的交易中。

当qA≤qB时， 例 如qB=1.01×105kWh， 用户B 的大部分电量均由大型联盟C 提供，此时小型电厂A 报价对于用户B 收益的影响将变得很小，可以忽略小型电厂A 而将三人博弈的模型可简化为二人博弈情形，用户B 最终将“屈服”于大型发电联盟C“强硬”的报价，市场在(0.25，0.25)达到均衡。而小型电厂发现市场的价格规律后，将会放弃之前的低价抢量策略，而选择加入到发电联盟中来以获取收益。在此种情形下，大型发电联盟可以行使市场力[15]。

表5 用户B报价

3.4 发电联盟的报价策略

上一个模型中，为了简化我们假设大型发电集团联盟C 的报价pC=0.25 元/kWh保持不变，现继续考虑市场供求基本平衡倾向下大型发电集团联盟C 的报价策略。

当qA≤qB时，市场的价格由发电联盟C 决定。容易看出发电集团联盟C事先约定的报价pC越高，则发电集团联盟C 最后的发电收益越高。所以其报价pC将趋向于超用价格pU，以获得最大利润。

而当qB≤qA时，市场价格由小型电厂和用户决定，此时采用发电联盟C 报高价将无法成交而只能按照pG结算，利益受损。故此情形下发电联盟将在利益驱动下自行解散，分散地在市场中争抢用户电量。

4 结束语

本文从博弈论的角度，对云南日前电量市场中的报价行为进行了研究和分析。通过简化的双人博弈模型和考虑发电联盟的三人博弈模型分析得到，日前电量市场的供求关系可直接影响日前电量价格及发电企业的最优报价策略。在严重供大于求的情形下，大型发电集团组成发电联盟将会使自身利益受损，不参加联盟的小型电厂则将因此收益；在供求基本平衡的情形下，大型发电集团组成发电联盟将可以操控市场价格，获取超额利润，其存在组建价格联盟并哄抬电价的潜在动机，可考虑采取措施限制其市场力。