基于历史 重构教学 深度学习

汪慧莲

摘 要：本文试着从负数的历史入手，对多套教材对正负数定义进行比较，基于历史，梳理脉络，通过前测把握学生的认知起点，教学时通过问题驱动，基于体验，感知相反意义，基于探究，关注“0”分界点，基于练习，发展高阶思维，深度度建构负数意义。

关键词：负数；深度学习；建构；意义

一、缘起：学生理解“负数”

接到一节市级公开课的任务，内容是《认识负数》，回想起自己多年前教学负数，总是要让学生先背负数的意义。但那时的学生真的的理解负数了吗？显然没有。负数的意义是背下来的，基本背的滚瓜烂熟。我们学数学，也沿用语文的路径：读书百遍，其义自见。

二、晰义：负数是怎么来的

深度学习的源点：结合历史，把握本质——为有源头活水来

“负数”属于概念性知识，它的产生、发展、运用必有一个漫长的过程，教材仅把它作为背景知识进行介绍，笔者觉得是不够的。在查阅大量的历史资料后我们发现中国对于负数的产生、认识与西方国家有着明显的区别。

（一）负数在中国的发展史

在我國古代，人们早有买卖等商品交易，期间慢慢地产生了负数。后来数学家刘徽在注解《九章算术》时，更明确地提出了正负数的概念。负数在中国的产生更多的是因为人们在生产生活中需要一种表示“亏损”、“下降”、“支出”的数。古代中国人对负数的认识和使用，鲜明地烙上了生活经验的痕迹。

（二）负数在外国的发展史

印度是认识和使用负数比较早的国家，其最早记载见于《婆罗摩历算书》中，他把正数称为“财产”，负数称为“债务”。而在西方，大多数学家并不接纳负数，直到1637年，法国大数学家笛卡儿发明了解析几何学，创立了坐标系和点的坐标概念，负数才获得了几何意义和实际意义。

所以，从数学史的视角来看，“负数”的教学无疑要关注：

1.是要引发学生学习新数的情感需求；

2.是要寻找承载负数本质意义而又直观的教学模型，以顺应抽象认识源于直观模型的心理顺序；

3.是要注重沟通负数和0之间的关系，以避免以后学习的认知障碍。

三、实践：怎样建构负数

张奠宙在《多多注意数学本质的揭示——剖析“用温度计引入负数”的优缺点》一文中给出了三条建议：首先，引入负数，一开始就明确提出“意义相反的量”的概念；其次，要先给出“0”点，然后才能谈正数与负数；最后，引入负数不能只用温度计模型，更重要的是用收入支出、赢与输等自然意义下的动态模型。根据以上3条建议我尝试进行了《认识负数》一课的教学设计，以问题驱动，深入学习。

（一）基于体验，感知相反意义

以“假如这个世界没有负数可以吗？”问题为驱动，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。

问题1：假如这个世界没有负数可以吗？

生：如果没有负数，计算减法时，不够减时，无法表示。

师：听得懂他的意思吗？没有负数就不可以了吗？

生①：可以用文字表示，比如：零下五度。生②：如果是计算，没有单位怎么表示呢？

问题2：你知道负数的由来吗？

活动：介绍数学史料

中国是最早认识和使用负数的国家。据古代数学名著《九章算术》记载，早在2000多年前我国古人就有了“粮食入仓为正，出仓为负；收入的钱为正，支出的钱为负”的思想。

1700多年前，我国数学家刘徽首次明确地提出了正数和负数的概念。他还规定筹算时“正算赤，负算黑”，就是用红色算筹表示正数，黑色算筹表示负数。这个记载，比国外早了十八百年。

追溯数学知识的历史渊源，并尽可能还原数学知识的发生和发展，让学生经历数学知识“再发现”、“再创造”的过程。

（二）基于探究，关注“0”分界点

以“0是正数还是负数呢？”问题驱动，一个负数总是某个正数的相反数，而“0”则是正数和负数的分界点，所以在引入负数概念的初期，就必须对“0”这个分界点给予特别关注，没有“0”，正负的概念无从谈起。

问题1：0是正数还是负数呢？

生①：我认为0既不是正数，也不是负数。生②：我认为0既不是正数，也不是负数。正数负数是以0为分界的。

师：出现了两种不同的意见，到底哪种有道理呢？先不着急。

介绍人为规定相反的量：温度，海拔，并以收入与支出、盈利与亏损、温度、海拔为例，追问：这时候的“0”在哪里？指出这里“0”的规定背后的合理性及其意义。

师：现在，你的想法有没有改变？

生①：我认为0既不是正数，也不是负数，0是分界线，是标准。

张奠宙先生指出，所谓意义相反的量其实就是两类：一类就是自然意义的相反，如收入与支出，0就是平衡点，另一类则是人为规定的相反，如水的结冰为0。从这两类相反的量深入体会“0既不是正数，也不是负数”。

问题2：身高可以是负数吗？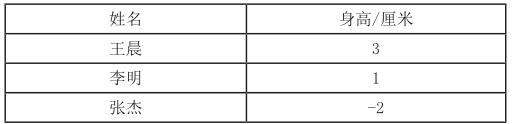

以“身高可以是负数吗？”问题为驱动，当学习材料一呈现，学生便会产生疑惑：身高怎么可能比0还要小？随着讨论的深入，谜团揭晓：由于定了一个标准量0，才会出现这些身高。

身高可以是负数吗？生①：不可以，没有这么矮的人。生②：可以，0界线是160厘米。师测量身高时李老师有一个标准0，就是165厘米。你知道他们实际身高吗？

生：王晨身高168厘米，李明身高166厘米，张杰身高163厘米。

总之，深度学习的核心是理解用怎样的教学方式提高学生的概念理解水平是需要教师不断研究的永恒主题。教师应该高屋建瓴地深入理解，准确把握学情，精心设计每一个问题，每一道习题，有序推进，帮助学生深度建构，发展数学的高阶思维。

参考文献

[1]全日制义务教育数学课程标准（实验稿）[M].北京：北京师范大学出版社，2001.

[2]孟佩娟，章立平.探寻“认识负数”教学的基本要点[J].中小学数学（小学版），2010（11）：32-34.