基于数值模拟的土压平衡盾构机施工效率优化

何同继，张怀鹏，苏留锁，赵光营，谢皆睿

(中铁十六局集团 北京轨道交通工程建设有限公司， 北京 100018)

现在社会功能集中，人口众多，因此，城市交通功能的完善是非常重要的。由于城市空间的高密度利用，为了保护城市景观和环境，需要在地下建设地铁、公路、供水系统、污水系统、电力线路、电信网络等组成的基础设施[1]。目前，我国许多城市都在运行大量的地铁和轻轨，还有更多的地铁和轻轨正在建设中[2]。EPB盾构机因具有环保、快速及对周围环境影响较小等优点，被广泛应用于市政、矿山、交通、水工等隧道工程施工中。刀盘作为土压平衡盾构机的核心部件，由于刀盘不同技术参数的应用直接影响刀盘的切削效率，所以刀盘技术参数的应用也是一个核心问题。盾构机在开工时都有一段试掘进过程，目的为了找到合适的刀盘挖掘速度和旋转速度。但是这个过程非常繁琐，一般很难找到合适的刀盘挖掘速度和旋转速度，而且对工期和盾构效率有很大影响。目前鲜有对刀盘挖掘速度和旋转速度研究的报道。因此对EPB盾构机刀盘重要技术参数之间的关系研究，对盾构法施工具有极其重要的意义。

目前，国内学者对盾构机刀盘模拟切削的研究较多。陈馈等[3]采用ANSYS软件对刀盘的应力分布进行分析，得到了刀盘刮刀承受轴向分力的分布规律。夏毅敏等[4]通过单因素分析了贯入度与刀盘转速对刀盘总扭矩的影响，并对比工程实际数据对其进行了验证。蔡宝等[5]对刀具布置的重叠量等关键参数进行研究，模拟了3种地质工况下刀群的切削过程。李守巨等[6]采用有限元数值仿真分析方法，研究了切刀切土开始阶段和平稳阶段的动态阻力特性。

从目前的研究成果来看，目前还没有对刀盘的旋转速度、挖掘速度和切削率之间关系研究的报道。本文采用通用有限元分析软件ABAQUS建立了在粉砂地层条件下盾构机刀盘挖掘的动态仿真切削模型，基于仿真结果，讨论掘进过程中土体的变形破坏过程及刀盘受载情况。并利用回归分析得出刀盘技术参数和切削效率之间函数关系。

1 工程和地质条件

1.1 工程概况

某城市地铁施工路段，其底板座落在③层—⑤层粉砂层土层上，车站标准段基坑深度在15.61 m左右,盾构井段深约17.4 m。

1.2 地质条件

地铁施工的地质条件如图1所示。

由图1可知，盾构机掘进主要通过的地层为：杂填土①②层、黏质粉土②③①层、砂质粉土夹粉砂②④②层、粉砂③⑤层、淤泥质粉质黏土夹粉土⑥②层、淤泥质粉质黏土⑥③层、黏土⑧①层和粉质黏土⑧②层。根据天津地铁4号线的施工地质情况，本文以粉砂③⑤层为研究对象。

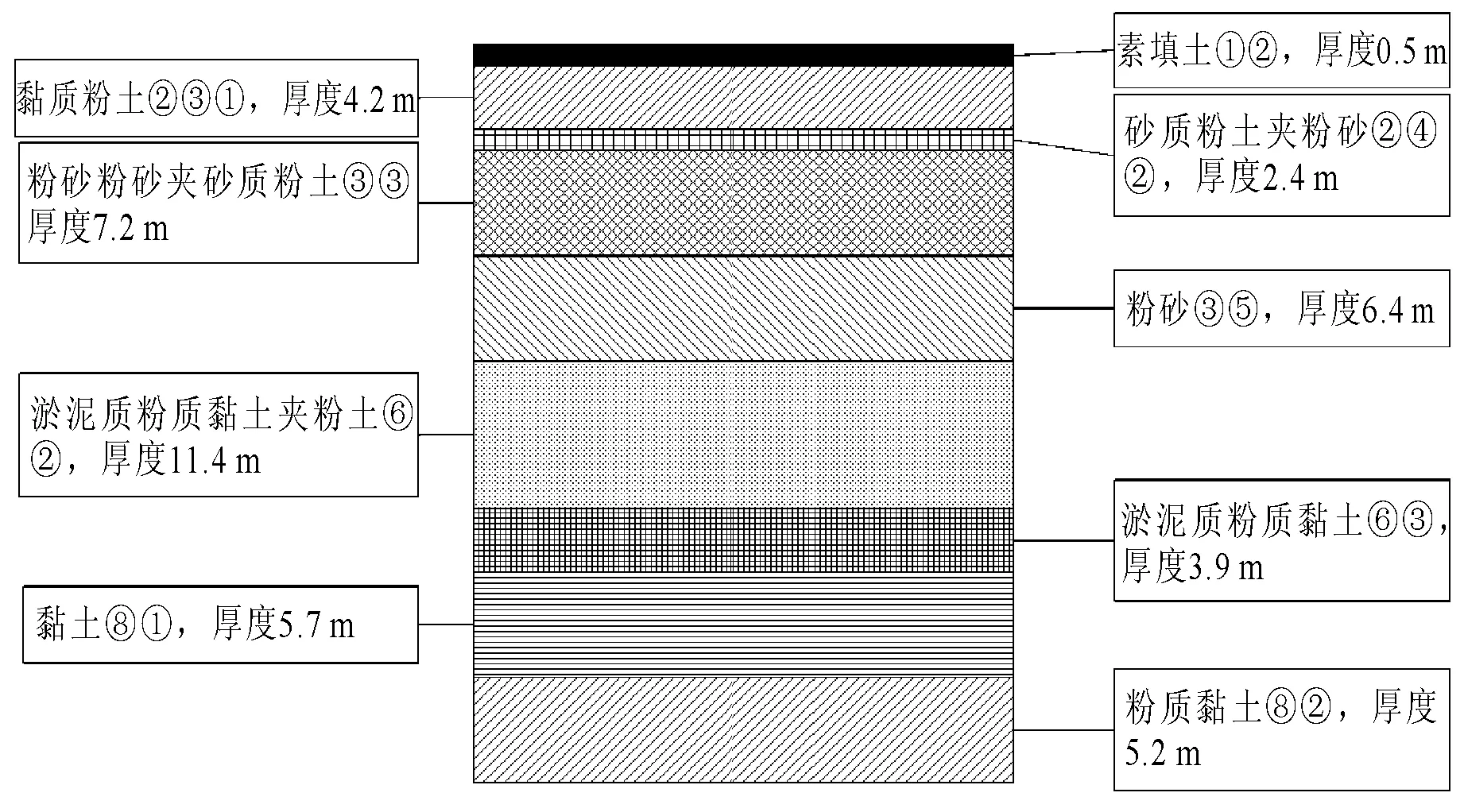
图1 地质条件

2 土体和刀盘模型

2.1 土体的本构模型及损伤失效准则

采用任意拉格朗日-欧拉方法(ALE)处理土体的大范围变形和破坏问题。土体和刀盘之间的接触关系采用对称罚函数。为了避免土体发生畸变和网格扭曲，在ABAQUS中应用土体的单元删除功能的剪切失效准则，采用ABAQUS/Explicit显示方法对刀盘切削土体进行数字仿真模拟。土体材料的本构关系通过非线性Drucker-Prager模型的屈服准则来模拟[7]。

损伤失效准则描述的是土体刚度逐渐丧失的过程。随着盾构机刀盘不断向前挖掘，首先，刀盘与土体接触。土体开始发生弹性应变，达到屈服强度后，按照一定规律土体逐渐失去承载能力，退出ABAQUS数值切削仿真计算。

2.2 建模及仿真过程

土体和刀盘的建模模拟过程如图2所示。

图2 建模模拟过程

首先通过SolidWorks三维软件建立刀盘的三维模型，ABAQUS有限元软件建立土体的三维模型。然后采用ABAQUS设置刀盘和土体模型的材料参数、定义装配体、设置分析步和输出项、设置边界条件和施加载荷、划分网格、进行模拟分析和对模拟结果进行分析。

2.3 土体和刀盘模型建立

采用阿基米德螺旋线刀盘刀具的布置方法和刀盘刀具的等寿命准则，利用SolidWorks三维软件建立刀盘的三维模型如图3(a)所示，刀盘直径为6.4 m，刀盘开口率为33%。为了能够较好地模拟刀盘切削土体的过程，运用ABAQUS/CAE前处理程序，建立土体的三维模型，其三维尺寸为7 m×7 m×2 m。通过定义刀盘切削土体装配体的三维模型如图3(b)所示。

图3 刀盘切削土体的三维模型

通过查找参考文献得，土体和刀盘的物理力学参数如表1所示[2，4，9-12]。

表1 土体和刀盘参数

2.4 仿真技术设置

在ABAQUS的Step-1分析步中设置刀盘挖掘速度10 mm/min、15 mm/min、20 mm/min、30 mm/min、40 mm/min、50 mm/min和80 mm/min分别对应Step-1中的分析步时间为15 s、24 s、30 s、40 s、60 s、80 s和120 s。增量设置为自动，在场输出中选择Mises(应力)、PEEQ(塑性应变)、U(位移)、STATUS(状态)，历史输出项中选择RF(支反力)。在仿真中将刀盘设置为刚体，在刀盘的中心设置参考点RP，然后对整个刀盘施加刚体约束。对刀盘参考点施加z方向的进给速度和旋转速度，同时设置刀盘沿x、y方向的位移约束和转动约束；对于土体模型，未与刀盘接触z方向表面设置为全固定约束，沿x、y方向四个表面采用对称位移约束，与刀盘接触表面设置为自由表面。刀盘与土体模型的边界条件和刚体设置情况如图4所示。

图4 刀盘与土体模型的边界条件

模型网格划分：对土体和刀盘模型采用三维线性减缩积分六面体单元(C3D8R单元)划分网格，土体模型网格近似全局尺寸为0.08 m，刀盘模型网格近似全局尺寸为0.02 m。土体和刀盘模型的网格数目分别为193 600个和14 365个，土体和刀盘模型的节点数目分别为205 946个和22 344个。

盾构刀盘Step-1分析步中挖掘距离为20 mm。本文设置了42组试验。

3 刀盘切削土体的仿真结果和分析

3.1 刀盘切削土体效率

刀盘切削土体的效率通过岩土质量随时间的变化来表征。当挖掘速度为10 mm/min时，土体质量随切削时间变化曲线如图5所示。由图5可以清晰地对比出不同挖掘速度和转速下刀盘刀群的切削效果，土体模型质量有明显的下降趋势，在t=0 s时刀盘开始与土体接触，随着时间的推进，土体模型强度极限后不断被破坏脱离下来，进而土体模型的质量不断减少直至切削完成。

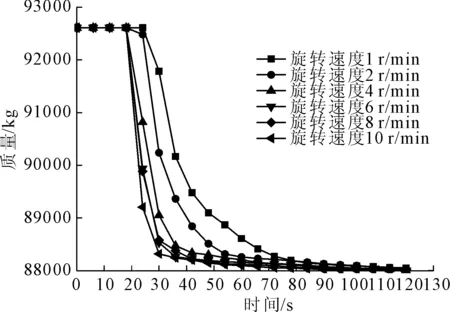
图5 岩土质量随时间变化曲线(挖掘速度10 mm/min)

由图5可知，土体质量变化曲线可以分为三个阶段：第一阶段土体还没有达到损伤准则，土体质量保持不变；第二阶段土体模型的塑性应变累计达到损伤准则脱离土体，土体质量开始迅速减少，减少速度逐渐降低；第三阶段土体质量减少缓慢或保持一定值，说明待切削土体剩余较少或土体切削完成。当刀盘旋转速度一定时，随着挖掘速度的增加，土体切削效率先保持不变，当挖掘速度继续增加一定值时，土体切削效率越来越小。土体模型质量变化统计如表2所示。

表2 土体质量变化统计

由表2可知，当刀盘旋转速度一定时，挖掘速度增加刀盘切削率先保持不变，随着挖掘速度的进一步增加，刀盘切削土体的切削率越来越小。为了土体达到最好的切削效率和减少盾构机的消耗，所以每一个旋转速度下对应一个最佳挖掘速度，其切削效率达到最佳，而且可以实现盾构机的消耗达到最低。

3.2 不同旋转速度下刀盘受到的作用力、作用力矩对比

刀盘在掘进过程中的受力和力矩情况，通过输出刀盘控制点RP的受力来反映刀盘整体的受载情况。刀盘的轴向力和力矩在切削过程中起到关键作用，当挖掘速度为40 mm/min和不同旋转速度下刀盘的轴向受载情况如图6所示。

为了更好的表述刀盘在不同转速和挖掘速度下的受载情况，将刀盘三个方向的力Fx、Fy和Fz(其中Fx和Fy为垂直于刀盘轴向的相互垂直力，Fz为轴向力)和其对应力矩Mx、My、Mz进行期望和方差的数学统计，统计结果如表3所示。

由图6和表3可知，在同一旋转速度下，当刀盘旋转速度一定时，刀盘受到的轴向力Fz和力矩Mz的值，随时间的增加呈现出先增加后减少的趋势。当挖掘速度一定时，刀盘三个方向受载力Fx、Fy和Fz的值，随刀盘旋转速度的增大有增加的趋势；其刀盘三个方向的力矩和对应力的受载情况相同。由图6可直观的分析出刀盘的受力情况，增加挖掘速度有助于减少刀盘的受载波动，施工时可通过设置合适的挖掘速度来减少刀盘的波动。当刀盘轴向力达到最大值时，即对应图6(a)中的N点，此后土体单元开始塑性应变累积，达到破坏失效准则脱离土体模型。刀盘力矩也是刀盘掘进过程中的重要参数，通过对比图6中刀盘力和力矩的变化规律，可以直观的看出刀盘轴向力和对应力矩都呈现出先增加后减少的趋势。

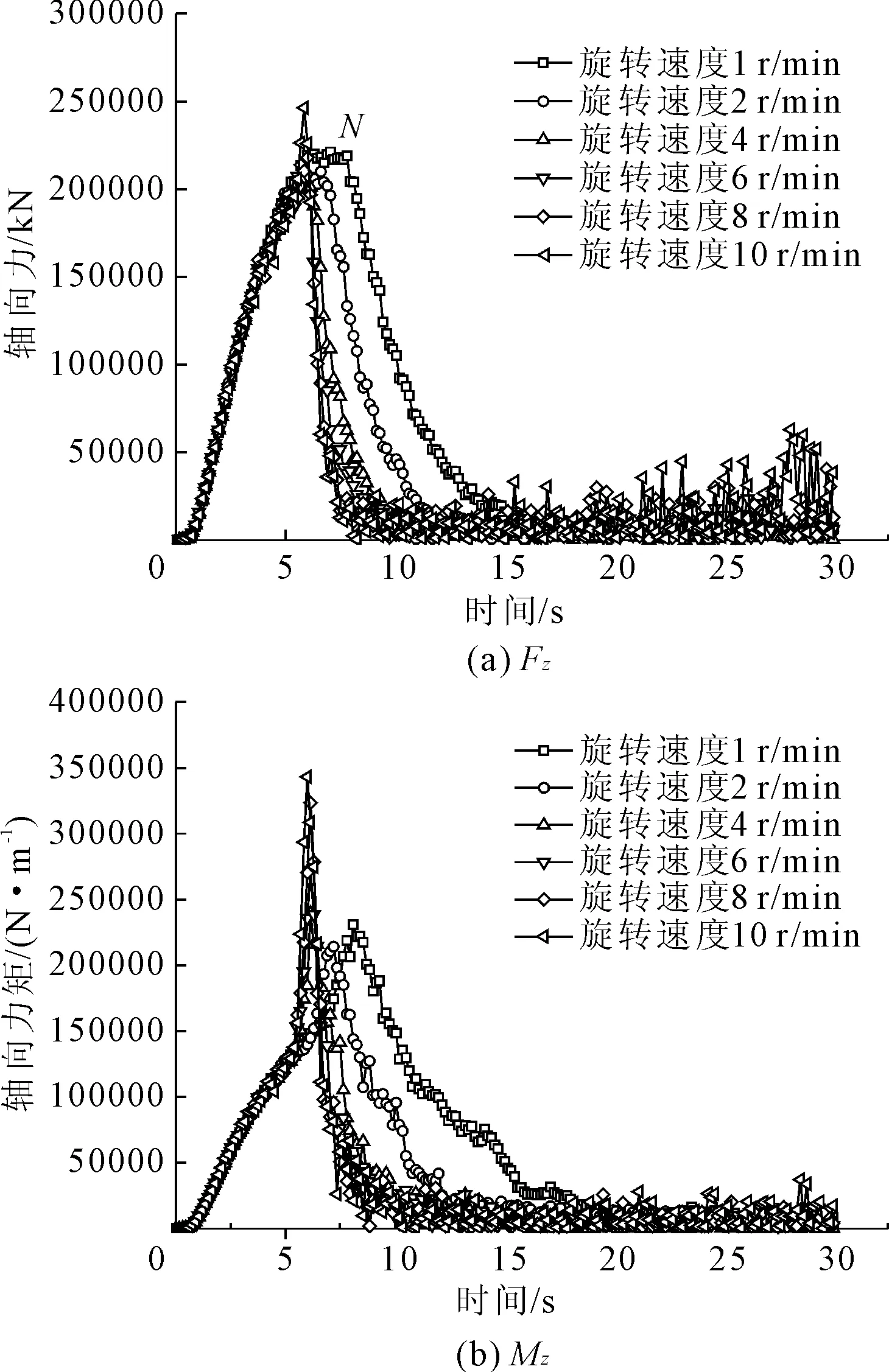
图6 刀盘不同转速和挖掘速度下刀盘的受载情况

4 回归分析

为了使土体切削效率达到最佳，并且盾构机挖掘的消耗尽量降到最小，需找到刀盘挖掘速度、转速和土体切削率之间的对应关系，下面将对刀盘的技术参数进行数学回归分析。

表3 刀盘受力数学统计分析

根据结果分析可知刀盘挖掘速度、转速和土体切削率三者之间近似存在函数关系。采用数学回归模型公式z=z0+ax+by+cx2+dy2+fxy进行回归分析，x代表旋转速度、y代表挖掘速度和z代表切削效率，分析得出数学模型公式中的系数如表4所示。

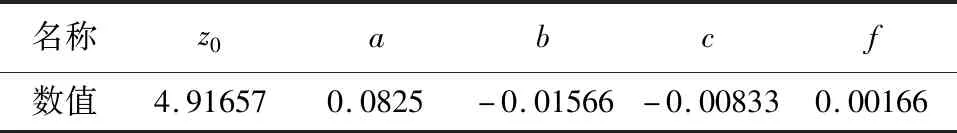
表4 数学模型公式系数

将表4中的数据带入回归数学模型公式得：

z=4.91657+0.0825x-0.1566y-0.00833x2+0.00166xy

(4)

通过公式(4)得刀盘挖掘速度、转速和土体切削率之间的三维关系如图7所示。

图7 刀盘挖掘速度、转速和土体切削率系数关系曲面

由图7和数学公式(4)可知，当刀盘转速一定时，随着刀盘挖掘速度增加土体减少量与总量比率越低；当刀盘挖掘速度一定时，随着刀盘转速增加土体减少量与总量比率增大。当刀盘切削的土体减少量与总量比率点达到最大时，对应一组刀盘转速和挖掘速度。

由某地铁盾构机设备可知实际刀盘转速为1 r/min～8 r/min之间，通过式(4)可得出，在土体减少量与总量比率达到最大时，刀盘转速和挖掘速度之间的对应关系如图8所示。

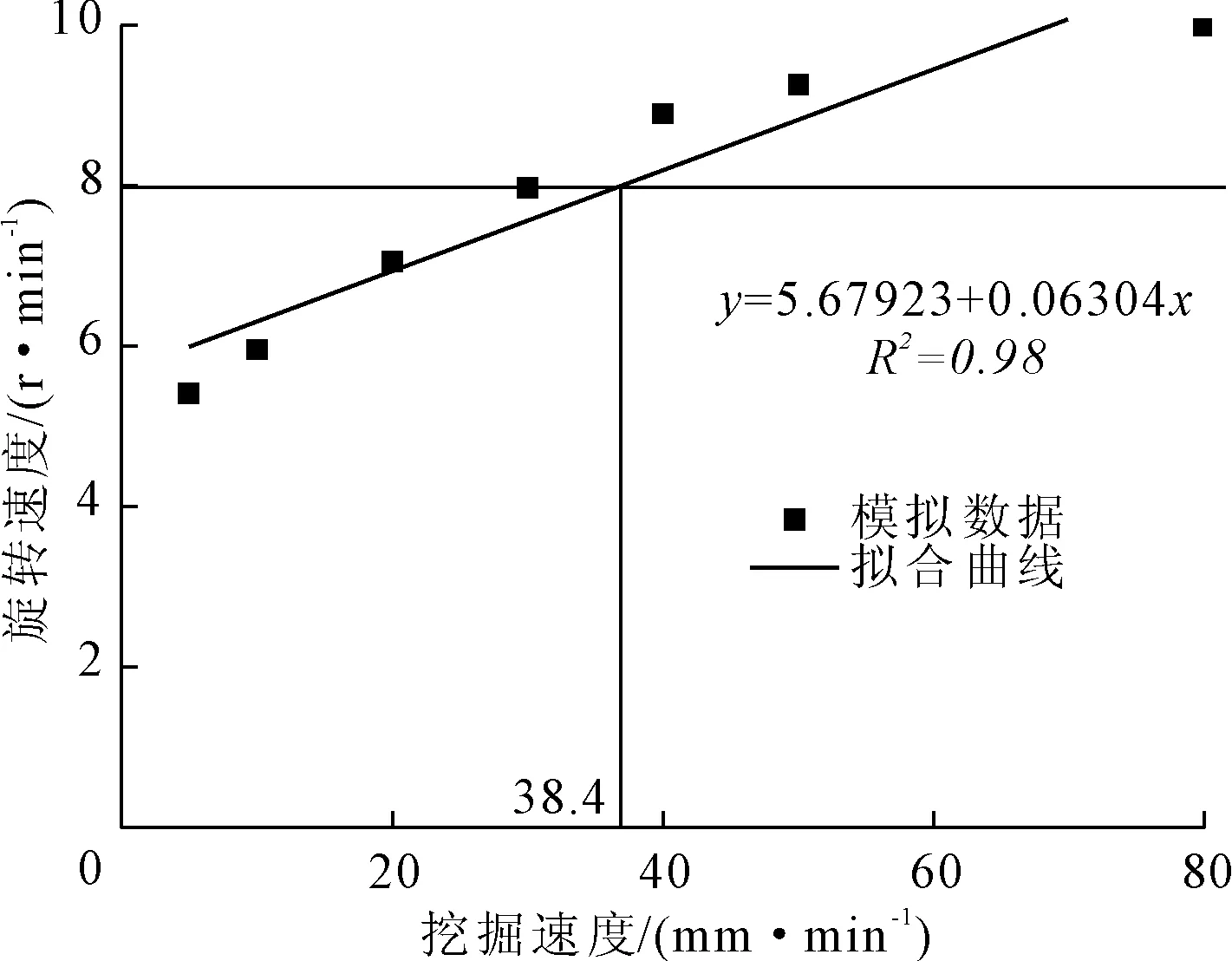
图8 刀盘转速和速度的关系

由图8可知，刀盘的旋转速度和挖掘速度成一定的正比关系，刀盘转速处于6 r/min～8 r/min之间时，土体减少量与总量比率达到最大，在刀盘转速为6 r/min、7 r/min、8 r/min时的土体减少量与总量比率最大值分别为5.058 46%、5.010 07%、4.980 08%，初步选择刀盘转速为6 r/min。在图6和表4的刀盘受载力学分析中，在刀盘转速为6 r/min、7 r/min、8 r/min时刀盘受到的轴向力分别为32 507 N、49 808 N、54 775 N，刀盘转速和速度值较小时，对应的刀盘受载也减少。考虑到刀盘的受载波动和磨损，选择刀盘转速为6 r/min时，相对可以延长刀盘的使用寿命，综合上述分析最后选择刀盘转速为6 r/min和挖掘速度为10 mm/min。该理论结果可以为接下来的刀盘开口率选择提供依据，也可以为某地铁盾构施工提供一定的理论参考。

5 结 论

本文以某地铁施工路段为背景，通过ABAQUS有限元软件对刀盘挖掘速度和旋转速度技术参数之间的关系进行数值仿真模拟研究，得出以下结论：

(1) 采用ALE法较好地解决了刀盘土单元的大变形、土破坏和土的相互作用问题。

(2) 刀盘在同种土体进行切削时，随着转速的增大，最大应力呈现出先增大后减少。土体的塑性应变云图和土体应力一应变曲线成一一对应的关系。

(3) 当挖掘速度一定时，刀盘三个方向受载力Fx、Fy和Fz的值，随刀盘旋转速度的增大而增加；刀盘三个方向的力矩和对应力的受载情况相同。

(4) 土体的切削效率呈现出三个阶段，第一阶段，土体模型质量保持不变；第二阶段，土体质量迅速减少到一定值；第三阶段，土体质量基本保持不变或有少量的减少。

(5) 通过对刀盘挖掘速度、旋转速度参数和减少量与总量比率的模拟结果进行回归分析，得到回归数学模型公式。