基坑坑角角度对空间效应影响研究

高 幸，贾金青，朱彦鹏，王旭春，陈进杰，程良奎

(1.河北建科唐秦建筑科技有限公司， 河北 唐山 063009；2.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024；3.兰州理工大学 甘肃省土木工程防灾减灾重点实验室， 甘肃 兰州 730050；4.青岛理工大学 土木工程学院，山东 青岛 266033;5.石家庄铁道大学 交通运输学院，河北 石家庄 050043；6.中冶建筑研究总院有限公司， 北京 100088)

基坑作为一个具有长、宽、深的三维空间体系，势必存在空间效应。现今已有大量学者对基坑空间问题进行研究[1]，申海平等[2]提出了平面应变计算结果与空间效应影响系数的乘积可得空间变形的计算方法。郑诚等[3]、刘念武等[4]、任彦君等[5]、李浩等[6]对基坑阴角效应影响范围进行研究，提出了阴角效应影响范围与开挖深度之间的比例关系。高幸等[7-8]根据坡顶水平位移反算作用于悬臂支护结构的空间土压力发挥系数及土压力分布，并以此提出基坑设计优化方法。深入研究后又提出了基坑深度、坑角距离与坑角效应影响系数之间的函数关系。王成华等[9]、冯勇等[10]、胡勇等[11]、贾涛等[12]、周勇等[13]通过数值模拟和工程监测等方式证实了基坑工程中空间效应的存在。楼春晖等[14]、李镜培等[15]研究发现软土基坑同样存在明显的坑角效应。现今的空间效应主要围绕空间效应影响范围、基坑开挖深度及基坑边长的关系进行研究，而从未涉及基坑坑角角度变化对空间效应的影响。本文依托FLAC3D数值模拟软件[16]分析了基坑变角度(60°～140°)对基坑空间效应的作用，提出了基坑空间效应影响系数与基坑坑角角度、坑角距离之间的函数关系，并通过工程实例对其研究结果的合理性进行验证。

1 建立数值模型

本文主要研究基坑坑角角度变化对空间效应的影响，为确保所测基坑中部处于最大变形状态(平面应变状态)，基坑开挖深度取10 m，基坑一边取固定边长140 m[17]，坑角角度在60°～140°范围内递增变化。

依托石家庄某基坑工程勘察成果建立土体模型，由于所建基坑模型对称，土体模型取原模型1/4，长为200 m，宽为100 m，高度为30 m，模型尺寸涵盖基坑开挖影响的所有区域[15]。为避免支护结构对空间效应分析造成干扰，所建模型不施加任何支护。模拟过程中，选择Mohr-Coulomb模型当作土体的本构模型，并对各土层的重度、黏聚力和内摩擦角加权平均，进行计算。模型的土层力学参数，如表1所示。基坑坑角角度变化示意图如图1所示。

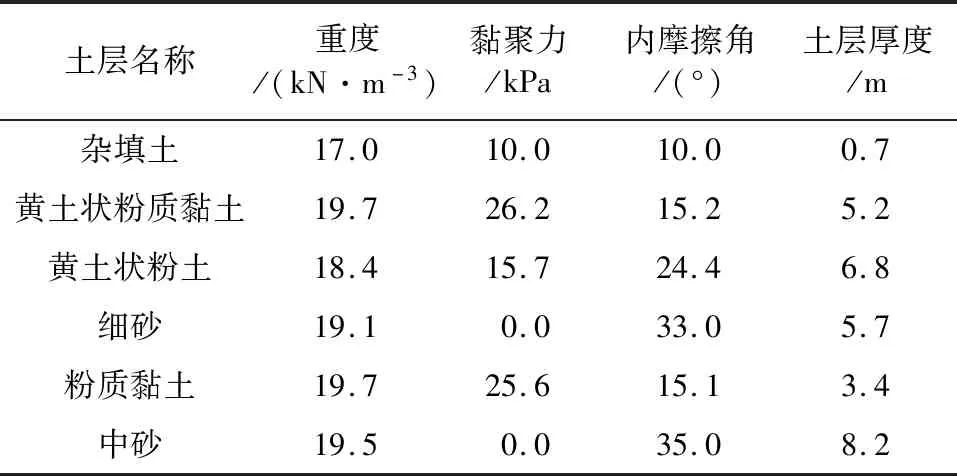
表1 土层力学参数

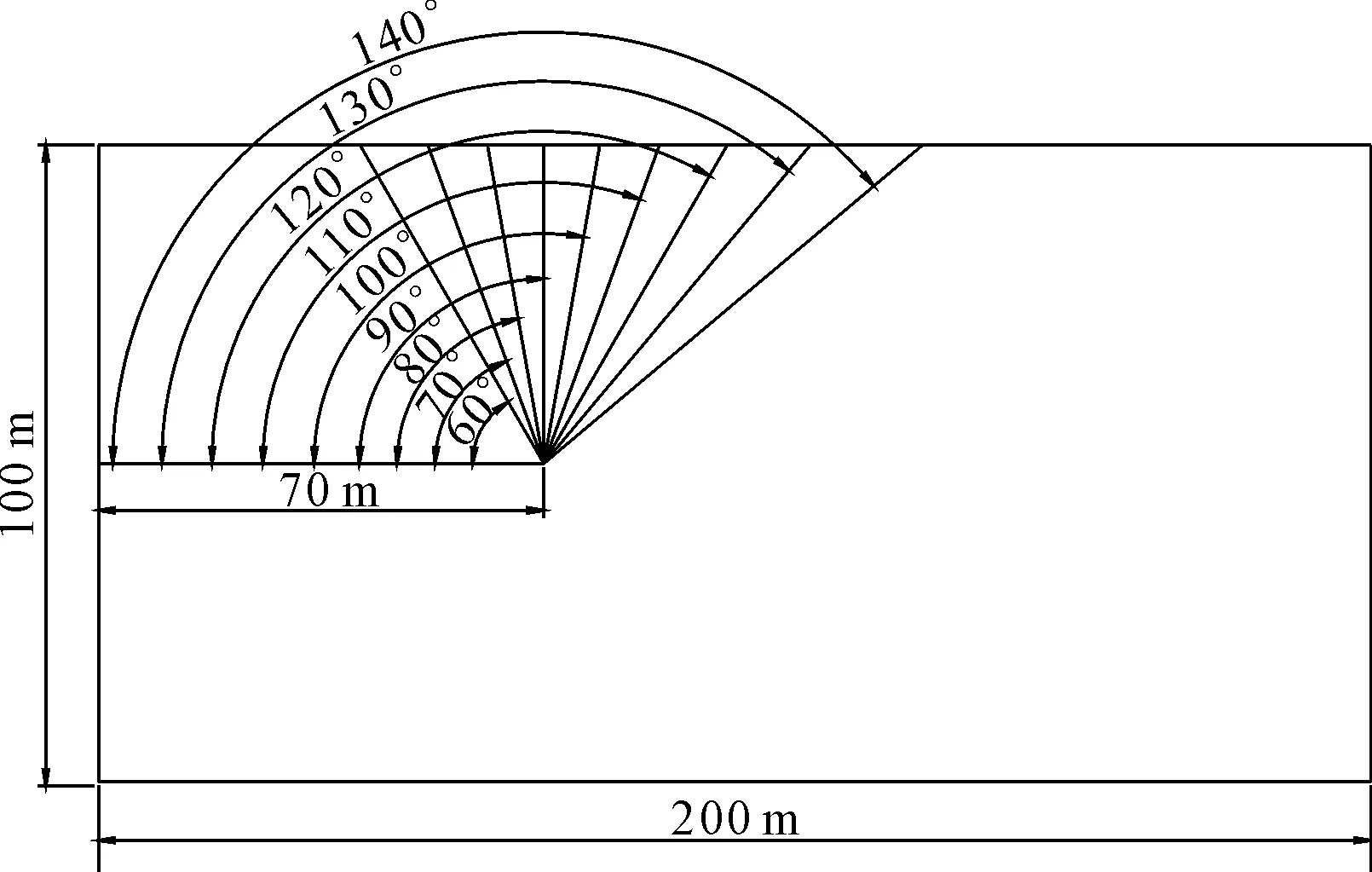
图1 基坑坑角角度变化示意图

2 坑角角度对空间效应影响分析

为量化分析空间效应的影响，提出空间效应影响系数概念，定义空间效应影响系数：K=w/wplane

其中，K为空间效应影响系数；w为坑边任意部位的顶部水平位移；wplane为平面应变问题对应的顶部水平位移。

为方便分析，本文对坑角距离和坑角角度无量纲化，转化为对x/L和α/180°进行研究。其中，x为坑角距离，L为基坑坑边长度，α为基坑的坑角角度。当α在60°～140°范围内变化时，K随x/L的增大而增大，K增大到一定程度时，不再随x/L的增大而继续增大，其变化曲线与指数函数变化曲线相似。

当α/180°=任意常数时，采用指数函数进行拟合：

K1=A1exp(-ζ/t1)+w1

(1)

ζ=x/L(无量纲)即坑角距离与基坑坑边长度的比值，ζ=[0，1]，K1为空间效应影响系数，拟合曲线如图2所示。

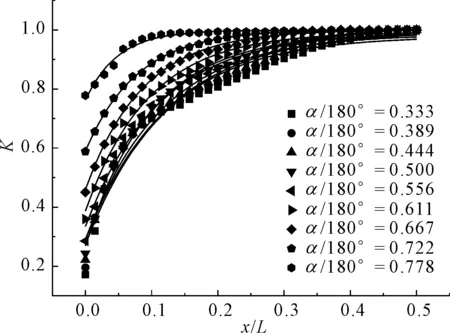
图2 不同α/180°下K与x/L拟合曲线

图3为K拟合值的相关系数随α/180°的变化曲线，其中相关系数越接近1表示拟合准确程度越高。从图中可以看出，所有拟合曲线的相关系数均大于0.96，拟合程度较高，说明坑角角度的变化不会改变K与x/L的指数函数关系。当α/180°在0.5～0.7(坑角角度为90°～130°)时，指数函数拟合程度更高，相关系数大于0.988。

图3 相关系数与α/180°的关系曲线

图4为K随α/180°的变化曲线，即基坑坑角角度与空间效应影响系数的相互关系曲线。不同x/L下，K随α/180°的变化特征存在明显差异。当x/L≥0.3时，无论α/180°为何值，K均大于0.9，基坑变形几乎处于平面应变状态。

图4 不同x/L下K随α/180°的变化曲线

当x/L<0.3时，发现K随α/180°变化关系亦呈指数函数形式，采用指数函数拟合：

K2=A2exp(-ζ/t2)+w2

(2)

ζ=α/180°(无量纲)即坑角角度与180°的比值，ζ= [0，1]，K2为空间效应系数。拟合曲线如图5所示，相关系数均大于0.95，曲线拟合度高，满足指数函数关系。

图5 不同x/L下的K随α/180°拟合曲线

由此可得到坑角角度与空间效应影响系数关系：当x/L≥0.3时，无论α/180°为何值，K均大于0.9，基坑变形几乎处于平面应变状态。当x/L<0.3时，K随α/180°变化关系呈指数函数形式。

图6为K、x/L和α/180°的关系曲线，从图6可见，任何一组x/L与α/180°均对应唯一的空间效应影响系数，由此可根据坑角度数，得出基坑坡顶任意位置的空间影响系数。由前文可知，K随x/L变化关系呈指数函数形式；当x/L≥0.3时，α/180°的取值对K基本无影响；当x/L<0.3时，K随α/180°变化关系呈指数函数形式。由此推导出x/L、α/180°与K的关系。推导过程如下：

图6 K、x/L和α/180°的关系云图

设x/L=X、α/180°=Y，K为空间影响系数

f(X)=A1exp(-X/t1)+w1

(3)

f(Y)=A2exp(-Y/t2)+w2

(4)

K=f(Y)f(X)

(5)

根据式(5)推导出

K=C1exp[(-X/t1)+(-Y/t2)]+

C2exp(-Y/t2)+C3exp(-X/t1)+C4

(6)

其中，C1=A1A2、C2=A2w1、C3=A1w2、C4=w1w2。

对函数采用麦夸特法(Levenberg-Marquardt) +通用全局优化法拟合，拟合结果如图7所示，相关系数大于0.99，曲线拟合度高，说明公式(6)可作为K、x/L和α/180°之间的函数方程。

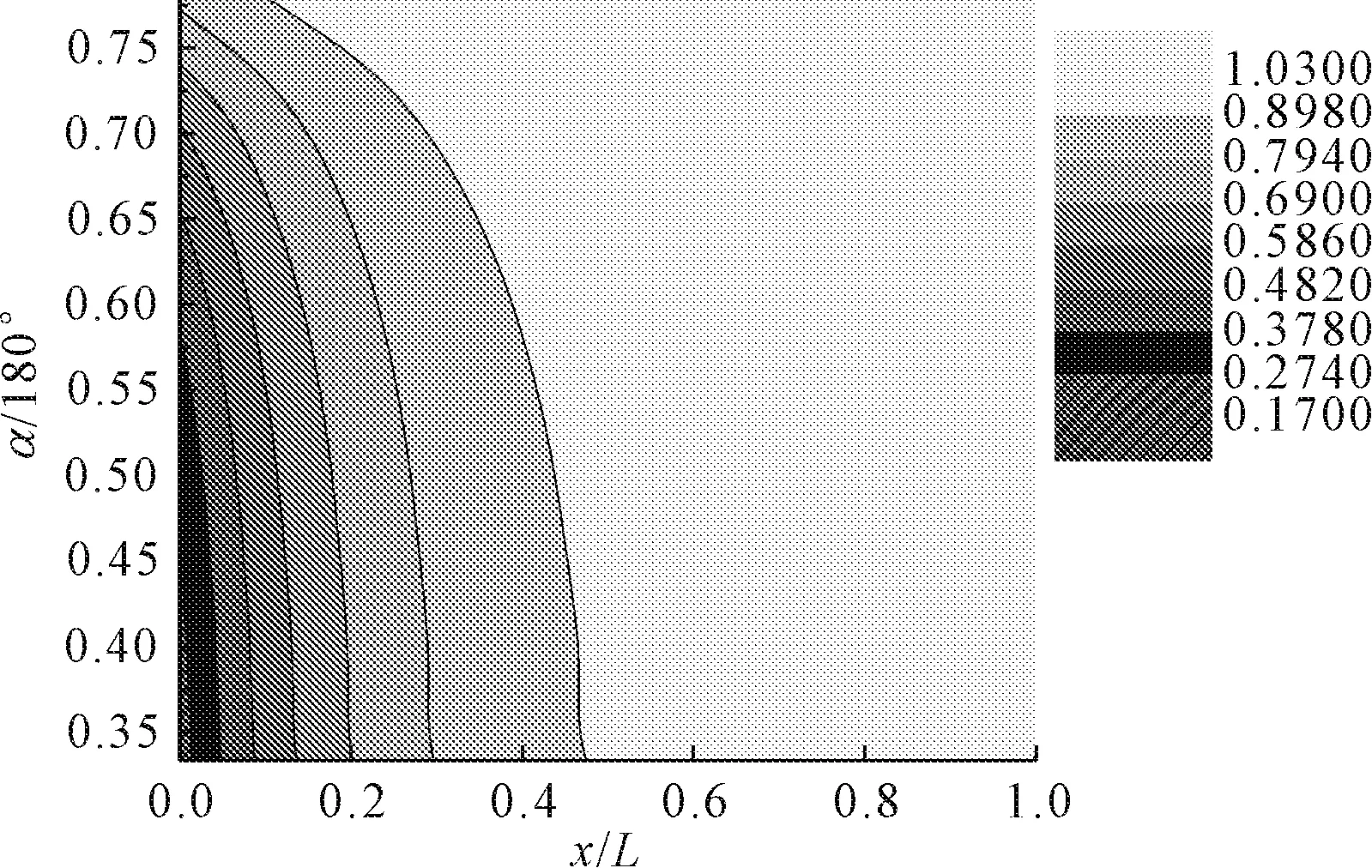
图7 K、x/L和α/180°的拟合关系云图

3 坑角角度对空间效应影响工程实例

该基坑位于石家庄市长安区翟营北大街与和光华路交口东南角。基坑支护设计采用护坡桩加锚索加止水帷幕形式支护。土层参数如表1所示，基坑尺寸平面图如图8所示。

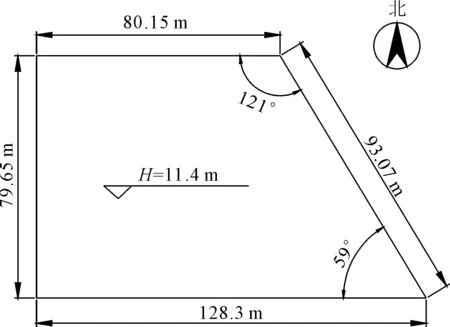
图8 基坑尺寸平面图

根据基坑监测数据计算空间效应影响系数，同时采用指数函数公式对基坑空间效应影响系数进行预测，对比监测所得空间效应影响系数与预测所得空间效应影响系数的关系。图9为基坑南侧东半边空间效应影响系数的实测值和预测值对比曲线，图10为基坑北侧东半边空间效应影响系数的实测值和预测值对比曲线。

从图9、图10中发现，不同坑角角度下空间效应影响系数预测值曲线与实测值曲线的变化趋势一致并且高度吻合。表明不同坑角角度下，基坑空间效应影响系数与x/L的关系，都可用指数函数公式进行预测。预测过程中，坑角角度为59°的预测平均误差为0.0357，坑角角度为121°的预测平均误差为0.0153，α为121°预测的K值比α为59°预测的K值更为准确，证实了当α/180°在0.5～0.7(坑角为90°～130°)时，指数函数拟合程度更高。

图9 基坑南侧空间效应影响系数的实测值和预测值对比曲线

图10 基坑北侧空间效应影响系数的实测值和预测值对比曲线

图11为不同x/L下，K随α/180°的变化曲线。由于本工程实例中基坑的坑角角度只涉及59°、90°、121°，现对这三个角度下的空间效应影响系数进行研究。

图11 不同x/L下的K随坑角角度变化曲线

从图11中可以看出，当x/L≥0.3，坑角为59°、90°、121°的空间效应影响系数分别在0.902，0.932，0.982以上，α变化对K基本无影响。当x/L<0.3，K随α/180°的增大而增大，且增大速率持续增大。由于数据有限，无法进行拟合，但其变化规律依然符合指数函数形式。

4 结 论

(1) 任何基坑坑角角度下，空间效应影响系数与坑角距离之间皆呈指数函数关系，且当坑角角度与180°的比值在0.5～0.7(坑角为90°～130°)时，函数拟合程度更高。

(2) 当坑角距离与坑边长度的比值大于等于0.3时，任何坑角角度下的空间效应影响系数均大于0.9且接近平面应变状态，当坑角距离与坑边长度的比值小于0.3时，坑角角度与空间效应影响系数之间呈指数函数关系。

(3) 根据空间效应影响系数和坑角距离的函数关系，空间效应影响系数和坑角角度的函数关系，推导出了空间效应影响系数、坑角距离和坑角角度三者之间的函数关系，并通过麦夸特法+通用全局优化法进行拟合，证实该函数关系的正确性。