基于序列递推的炉温曲线的优化研究

吕少梅

【摘  要】本文主要研究的是炉温曲线的优化问题，通过调整小温区的温度和传送带的速度使焊接符合工业生产要求，并且推算出最优炉温曲线。为解决这一问题，必须了解炉内空气间及炉内空气与电路板间的热传递。通过傅里叶传热定律及能量守恒定律可以推算出炉内环境温度呈分段线性变化，通过牛顿冷却定律可以根据附件的数据找出焊接区域中心温度变化规律。于是，本文利用序列递推的思想求解出不同时刻下的温度。

【关键词】炉温曲线;序列递推

引言

表面贴装技术（SMT）是目前电子组装行业中十分流行的一种技术和工艺，它具有组装密度高电子产品体积小、表面贴装元器件质量轻等优点。因此建立SMT的温度曲线优化技术的模型设计显得尤为必要。为了实现设计目的，通过利用实测回流焊炉温曲线，建立焊接区域温度变化的数学模型，优化炉温曲线。本文基于序列递推方法，求解不同时间段的焊接区域中心的温度，以及相应的炉温曲线。

1.问题分析

炉温曲线的设计问题，实质上是综合考虑各种方式，對其温度曲线建立模型，并应用于求解温度曲线分布和参数优化问题，模型的核心在于传热模型的建立及应用。

各温区的环境温度以及温区之间的温差影响情况已知，并且已知回炉内实验的温度变化曲线。求解温度分布，需要根据信息，综合考虑各种传热方式的运用情况，建立完整的模型，对于模型建立过程中的未知参数，通过模型建立将多个参数合并成为一个参数，并与数据进行拟合求解得到最优参数，并应用到之后的求解过程中。

2.模型的建立与求解

2.1模型维度及坐标系建立

回焊炉中的器件从几何形状上来说，属于三维传热模型，但是就本问题而言，由于：

（1）温区温度均匀分布，炉内温度仅在在一个方向进行，即沿传送带方向;

（2）无其他不均匀热源及传热过程，研究三维传热意义不大。

因此，我们对模型进行简化，假定垂直于传送带的平面温度相同，建立一维传热模型，仅研究炉内温度在沿传送带方向上的变化情况。

2.2传热方式

热量的传递主要有热传导，热对流和热辐射三种方式，不同的传热方式有其特点和适用情况。在炉内温度未达到稳定时，炉内环境的热量传动主要以空气间的热传导方式进行。在焊接的过程中，传热方式主要以对流和辐射为主，另外为了方便，在工程计算中经常把辐射传热换算为对流〖传热〗。

2.3傅里叶定律

在同一温度变化区间内，间隔相同的三个点间的热量传递关系满足傅里叶定律， 当炉内温度达到稳定时，根据能量守恒定律可以得出：

从中可以求解出在同一温度变化区间内，间隔相同的三个点间的温度变化相同，同一温度变化区间内的温度与传送带的位置呈线性关系。通过假定炉外温度恒定25℃，小温区中点位置稳定于小温区设置温度，炉内各点处的温度可以根据其满足的线性关系进行计算。

基于已知条件，我们计算得出炉内温度达到稳定后的分布情况。将点（0，25），（40.25，175，）（181.25，175），（217.75，195），（253.25，235），（288.75，255），（324.25，255），（359.75，25）代入公式，解出线性方程组系数，得出在简化下的条件下，炉内温度与沿传送带方向上的位置呈一一对应关系，有利于后续传热模型的建立。

2.4牛顿冷却公式

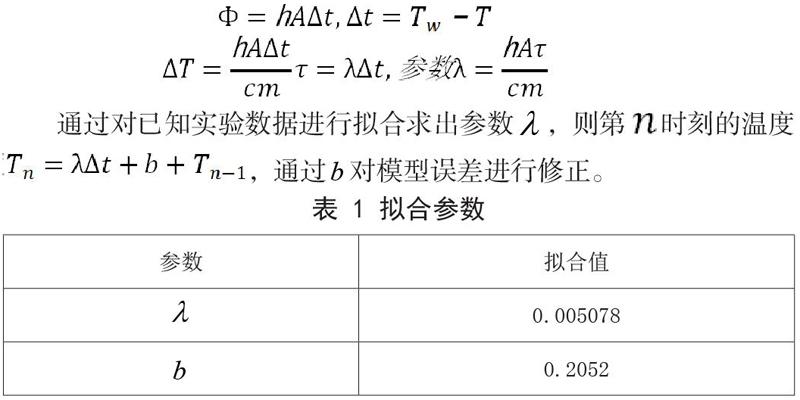
炉内环境与焊接区域的热量交换现象属于热对流，满足牛顿冷却公式：

通过对已知实验数据进行拟合求出参数，则第时刻的温度，通过对模型误差进行修正。

将拟合参数带入一维递推传热模型，电路板位置通过传送带速度与进入的时间相关联，即：

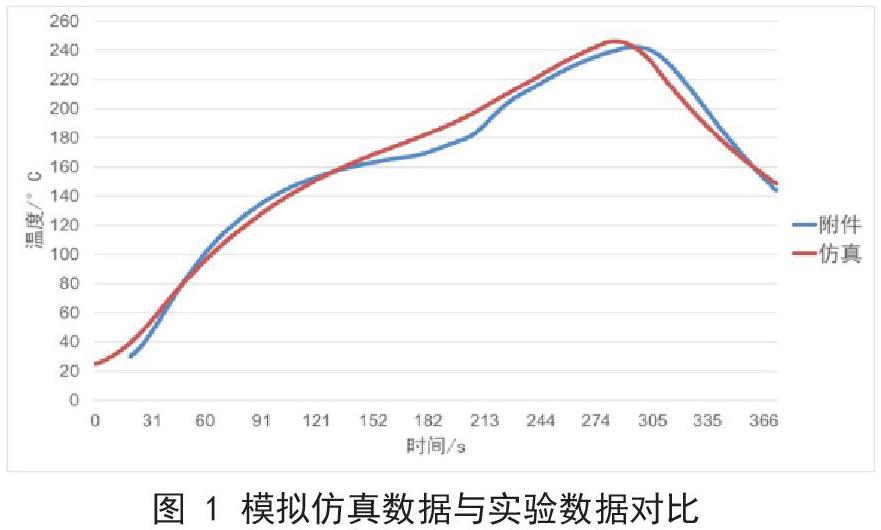
通过温度序列的递推关系既可得模拟仿真数据，下图画出模拟仿真数据与实验数据对比情况。

由图中可以看出有模型得出仿真数据与实际数据的误差较小，效果良好。

同理针对已经给出的参数设置，运用一维递推传热模型，计算出炉内环境温度分布和每个位置下焊接区域中心的温度，画出炉温曲线。

3.模型评价与改进

（1）根据合理的假设以及数学思维的转换将多个参数求解整合为单个参数求解减少模型复杂度;

（2）巧妙的利用递推公式与牛顿冷却定律之间的数值关系，构造了一维热传导模型;

（3）优化模型运用了智能遗传算法使得模型得优化不在局限于局部解。

参考文献

[1]黄丙元. SMT再流焊温度场的建模与仿真[D].天津大学，2005.

[2]赵镇南. 传热学 [M] . 第三版. 北京：高等教育出版社， 2019.