突破立几空间动点难题的若干策略

李锦昱

立体几何中的交线与截面问题是立体问题平面化的思想方法的体现，也是空间想象能力与推理论证能力考查的抓手，但其难度大，思维灵活，让很多同学倍感困惑.本专题从一道最新高考题入手，结合部分模拟题，剖析如何处理交线与截面问题.

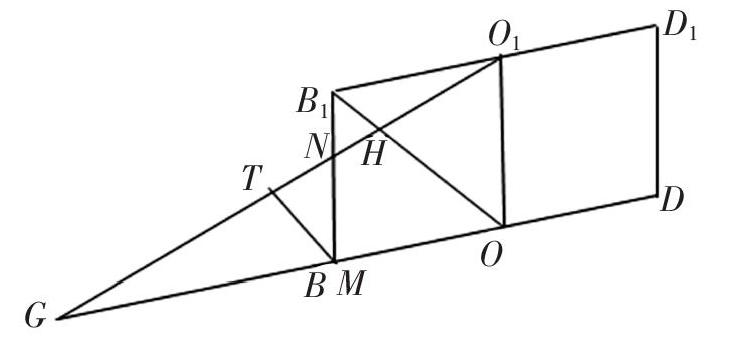
引例.（2020年新高考I卷（山东省使用）第16题）已知直四棱柱ABCD-A1B1C1D1的棱长均为2，∠BAD=■，以D1为球心，■为半径的球面与侧面BCC1B1的交线长为_____.

解析：设B1C1的中点为O1，则D1O1⊥侧面BCC1B1，且D1O1=■，侧面BCC1B1内以O1为圆心，■为半径的圆弧与BB1，CC1的交点分别为E，F，易知∠EO1F=■，则四分之一圆弧EF为球面与侧面BCC1B1的交线，其长度为■？仔.

思考：D1在侧面BCC1B1的射影为O1，则■的长通过驿站O1，转化为侧面内的圆弧EF，那么有对称性可知，球面与侧面ABB1A1的交线长是以A1B1的中点O2为圆心，■为半径的四分之一圆弧;D1在底面ABCD的射影为D，则■的长通过驿站D，转化为底面内的圆弧（半径为1，圆心角为■），球面与侧面ADD1A1，CDD1C1的交线分别是一段圆弧. 即球面与直四棱柱表面的交线可以作出来，当然其长度也能求出来.

溯源1（2020年日照二模）：已知正方体的棱长均为2，以正方体的一个顶点为球心，以2■为半径作球面，则该球面被正方体表面所截得的所有的弧长之和为_______.

简解：以D1为球心，则该球面被正方体表面所截得的所有的弧分别是底面ABCD和侧面ABB1A1， BCC1B1的以D， A1，C1为圆心（驿站），半径为2的三段四分之一圆弧AC， AB1，B1C弧长之和为3？仔.

溯源2（2020年青岛三模、多选）：在如图所示的正方体ABCD-A1B1C1D中，棱长为1，点P在侧面BCC1B1所在平面内运动，则下列命题中正确的為（）

A. 若点P总满足PA⊥BD，则动点P的轨迹是一条直线

B. 若点P到点A的距离为■，则动点P的轨迹是一个周长为2？仔的圆

C. 若点P到直线AB的距离与到点C的距离之和为1，则动点P的轨迹是椭圆

D. 若点P到直线AD的距离与到直线CC1的距离相等，则动点P的轨迹是双曲线

简解：对于选项A，由线面垂直（BD⊥对角面ACC1A1）易知动点P的轨迹是直线CC1;对于选项B，以B为圆心（驿站），半径为1的圆（以A为球心半径为■的球面与侧面BCC1B1的交线）;对于选项C，线段BC上的点到直线AB的距离与到点C的距离之和为1，故动点P的轨迹是不是椭圆;对于选项D，以BC，BB1分别为x， y轴建立直角坐标系xBy，设 P（x， y），则点P到AD， CC1的距离即x-1 =■，整理得（x-1）2-y2=1，其轨迹是双曲线. 故选ABD.

一、交线问题

1. 线面平行得直线（线段）.

例1.（2020年广州二模）在三棱柱ABC-A1B1C1中，E是棱AB中点，动点F是侧面ACC1A1（包括边界）上一点，若EF∥平面BCC1B1，则动点F的轨迹是（）

A. 线段 B. 圆弧 C. 椭圆的一部分 D. 抛物线的一部分

分析：由线面平行联想面面平行，设棱AC， A1C1的中点分别是M， N，则EM∥BC，MN∥CC1，平面EMN∥平面BCC1B1，故动点F的轨迹是线段MN，选A.

2. 球与平面的交线.

下面的问题从平面到空间都和形形色色的阿波罗尼圆有关的：

例2.（2020年合肥三模文科）点P是正方体ABCD-A1B1C1D1的侧面DCC1D1内的一个动点，若△APD与△BCP的面积之比等于2，则点P的轨迹是（）

A. 圆的一部分

B. 椭圆的一部分

C. 双曲线的一部分

D. 抛物线的一部分

分析：由线面垂直联想线线垂直，由AD⊥侧面DCC1D1，BC⊥DCC1D1，则■=■=2，PD=2PC，在侧面DCC1D1内，DC上靠近点C的三等分点为P1，延长DC到P2，使DC=CP2，则P的轨迹是圆（阿波罗尼圆），且直径为P1P2，选A.

例3.（2020年合肥三模理科）在长方体ABCD-A1B1C1D1中，AB=AD=6，AA1=2，M为棱BC的中点，动点P满足△APD=△CPM，则点P的轨迹与长方体的面DCC1D1的交线长等于（）

A. ■B. ？仔C. ■D. ■？仔

分析：由线面垂直联想线线垂直，由AD⊥平面DCC1D1，BC⊥平面DCC1D1，则∠APD=∠CPM，■=1，■=2，PD=2PC，在侧面DCC1D1内，DC上靠近点C的三等分点为P1，延长DC到P2，使DC=CP2，则P的轨迹是圆（阿波罗尼圆），且直径P1P2=8，半径为4，弧P1Q所对的圆心角为∠QOP1，交线长（弧长）为■，选A.

例4.（2020年济南一模）古希腊数学家阿波罗尼奥斯发现：平面上到两定点A，B距离之比为常数？姿（？姿>0且？姿≠1）的点的轨迹是一个圆心在直线AB上的圆，该圆简称为阿波罗尼圆.

如图，在长方体ABCD-A1B1C1D1中，AB=2AD=2AA1=6，点E在棱AB上，BE=2AE，动点P满足BP=■PE. 若点P在平面ABCD内运动，则点P所形成的阿波罗尼圆的半径为_____;

若点P在长方体ABCD-A1B1C1D1内部运动，F为棱C1D1的中点，M为CP的中点，则三棱锥M-B1CF的体积的最小值为___________.（本小题第一空2分，第二空3分）

解析：在底面ABCD内，在线段BE（长为4）上，由BP1=■P1E解得EP1=2■-2;在BE线段的延长线上，由BP2=■P2E解得EP2=2■+2，则P的轨迹是圆（阿波罗尼圆），且直径P1P2=4■，半径为2■，圆心恰好为顶点A.

若点P在长方体ABCD-A1B1C1D1内部运动，点P所形成的轨迹是以顶点A为球心，半径为2■的球面（被长方体所截的部分，可以理解为底面内的阿波罗尼圆绕直线旋转一周所形成的封闭几何体）. F为棱C1D1的中点，M为CP的中点，则三棱锥M-B1CF的体积的VM-B■CF =■VP-B■CF，体积最小值只需点P到底面B1CF（面积为定值■）的距离hP最小，可转化为点A到底面B1CF的距离hA减去球的半径2■，设AB的中点为点N，则点N到底面B1CF的距离hN满足hA=2hN，根据正方体的性质易知点C1到底面B1CF的距离hC■满足hN =2hC■，且hC■=■，故hA=4hC■=4■，hP≥hA-R=2■，VM-B■CF =■VP-B■CF≥■×■×2■=■. 故填2■，■.

點评：本题能够从平面到空间类比，得到点P的轨迹是球面（不妨称为阿波罗尼球）十分关键，且高（距离）从点M→点P再→点A直至→点N到平面B1CF的距离的一系列转化，充分体现了化归与转化思想.（当然，此题思维含量过高，推理复杂实为白璧微瑕）

二、截面问题

截面问题需要熟记三个公理和八个定理（线面平行和垂直的判定与性质定理、面面平行和垂直的判定与性质定理），并且有应用这些公理和定理的意识.

1. 利用线面垂直作截面

例5. 正四棱锥P-ABCD的底面边长为2，侧棱长为2■. 过点A作一个与侧棱PC垂直的平面？琢，则平面？琢被此正四棱锥所截的截面面积为__________，平面？琢将此正四棱锥分成的上下两部分的体积之比为__________.（本小题第一空2分，第二空3分）

解析：如图，△PAC是边长为2■的等边三角形. 底面的中心为O，由PO⊥平面ABCD，点M是△PAC的重心，BD⊥平面PAC，连接AM与侧棱PC交于点F，则F是侧棱PC的中点，过点M作GE//BD，则交点G、E分别是PD，PB的三等分点，平面AEFG是平面？琢被此正四棱锥所截的截面，其面积SAEFG=■AF·GE=■;又PC⊥平面AEFG，VP-AEFG=■SAEFG·PF=■，VP-ABCD=■SABCD·PO=■，则■=■，平面？琢将此正四棱锥分成的上下两部分的体积之比为■，故填■，■.

点评：本题实际上是考查了线面垂直的判定和性质的应用，表面积和体积的考查仅是入手点，感兴趣的读者可以计算下截面的周长.

例6.（2020年南昌二模）已知正四棱锥P-ABCD中，△PAC是边长为3的等边三角形. 点M是△PAC的重心，过点M作与平面PAC垂直的平面？琢，平面？琢与截面PAC交线的长度为2，则平面？琢与正四棱锥P-ABCD表面的交线所围成的封闭图形的面积可能为__________. ①2;②2■;③3;④2■.（请将可能正确的序号都填上）

解析：设底面的中心为O，由PO⊥平面ABCD，点M是△PAC的重心，BD⊥平面PAC，过点M作GE//BD，则交点G、E分别是PD， PB的三等分点，所作截面？琢必经过直线GE.

当平面？琢与截面PAC交线平行于AC时，截面是正方形EFGH，正四棱锥底面边长为■，EFGH的边长为■，其面积SEFGH =2;

当平面？琢与截面PAC交线平行于PA（或PC）时，截面是EFGHI，正四棱锥底面边长为■，△EFG为等腰三角形，其面积S△EFG =■×2×1=1，长方形EGHI，其面积SEGHI =2，故SEFGHI =S△EFG +SEGHI =3，故填①③.

点评：本题中所求截面？琢有三个要求：过点M、与平面PAC垂直、与截面PAC交线的长度为2，能转化到△PAC中过中心M的三条平行线（长度为2）.

2. 利用公理作截面

例7.（2020年聊城二模）已知点M， N分别为三棱柱ABC-A1B1C1的棱BC， BB1的中点. 设△A1MN的面积为S1，平面A1MN与三棱柱ABC-A1B1C1的截面面积为S，五棱锥A1-CC1B1NM的体积为V1，三棱柱ABC-A1B1C1的体积为V，则■=_________，■=_________.（本小题第一空2分，第二空3分）

解析：如图，延长NM， C1C交于点P，连接PA1交AC于点Q，连接QM，则A1QMN是截面，点M， N分别为棱BC， BB1的中点，则由相似形可得点Q是AC的三等分点.

不妨设侧棱垂直于底面，且A1C1⊥B1C1，则V=■A1C1·B1C1·CC1，V1=■A1C1·SCC■B■NM =■A1C1·B1C1·CC1，■=■;如图，在△PA1N中，点Q是PA1的三等分点PC交于点F，M是PN的中点，分别过点P，Q作A1M的垂线，则垂线段（距离）之比为3∶2，而点P， N到A1M的距离相等，因此，■=■，■=■，故填■，■.

点评：画截面要注意找出两个平面的交线（通常需要延长相关直线，以便确定两个公共点，进而得到公共直线），发挥三个公理的作用，面积和体积的计算则需要确定相应的比例.

3. 利用异面直线的公垂线作截面

例8. 已知长方体ABCD-A1B1C1D1中，AB=3，AD=2，AA1=1，则过BD1的截面面积的最小值为_______.

解析：如图，过BD1的截面与棱AA1， CC1分别交于点E， F，则截面BED1F是平行四边形，SBED■F =2S△BED■，点E在棱AA1上，点E到BD1的距离的最小值为异面直线AA1， BD1的距离，也就是点A1到B1D1的距离d1=■，BD1=■，截面面积SBED■F =■.

同理，过BD1的截面与棱AD， B1C1分别交于点G， H，则截面BGD1H是平行四边形，SBGD■H =2S△BGD■，点G在棱AD上，点G到BD1的距离的最小值为异面直线AD， BD1的距离，也就是点A到A1B的距离d2=■，BD1=■，截面面积SBGD■H =■.

同理，过BD1的截面与棱A1B1， DC分别交于点M， N，则截面BMD1N是平行四边形，SBMD■N =2S△BMD■，点M在棱A1B1上，点M到BD1的距离的最小值为异面直线A1B1， BD1的距离，也就是点A1到D1A的距离d3=■，BD1=■，截面面积SBGD■H =■.

因为d1

点评：本题中要想求截面面积的最小值，只需要求出三对异面直线之间的距离的最小值.

4. 利用等积转化作截面

例9. 直四棱柱ABCD-A1B1C1D1的所有棱长都是1，∠ABC=60°，AC∩BD=O，A1C1∩B1D1=O1，點H是线段B1O上的点，且OH=3HB1，点M是线段BD上的动点，则M-C1O1H三棱锥的体积的最小值为_______.

解析：如图，点H是线段B1O上靠近点B1的四等分点，由C1O1⊥平面BDD1B1，VM-C■O■H =VC■-MO■H =■S△MO■H·C1O1.

在对角面BDD1B1中，延长O1H，OB交于点G，且与BB1交于点N，由相似形可得N是侧棱BB1的靠近点B1的三等分点，点M是线段BD上的动点，则点M与点B重合时，△MO1H面积最小，O1H=■O1G=■. 此时，点M到O1G的距离MT=■=■，S△MO■H =■O1H·MT=■，VC■-MO■H ≥■×■×■=■，故填■.

点评：本题利用从空间中的等体积转化和平面中的等面积转化，轻松解决了空间中的运动变化问题，特别是在截面（对角面）中的计算非常巧妙，体现了类比与转化思想.

5. 利用空间到平面的类比和对称思想作截面

例10. 已知正三棱柱ABC-A1B1C1的所有棱长为2，点M， N分别在侧面ABB1A1和ACC1A1内，BC1与B1C交于点P，则△PMN周长的最小值为______.

解析：点P关于侧面ABB1A1和ACC1A1的对称点分别为P1， P2，连接P1， P2，与侧面ABB1A1和ACC1A1的交点分别为M， N，易知M， N是侧面ABB1A1和ACC1A1的中心，此时△PMN周长的最小，且最小值为3，故填3.

点评：本题可联想平面中，在角的两边上各取一点与角内的一点构成的三角形的周长最小问题，可以在中截面（或上下底面）中巧妙利用对称求解.

6. 利用空间空间向量确定动点个数

例11. 已知长方体ABCD-A1B1C1D1的棱AA1=2，AD=3，点E， F，分别为棱BC，CC1上的动点. 若四面体A1B1EF的四个面都是直角三角形，则下列命题正确的是_______.（写出所有正确命题的编号）

①存在点E，使得EF⊥A1F;

②不存在点E，使得B1E⊥A1F;

③当点E为BC中点时，满足条件的点F有3个;

④当点F为CC1中点时，满足条件的点E有3个;

⑤四面体A1B1EF四个面所在平面，有4对相互垂直.

解析：四面体A1B1EF的四个面都是直角三角形，则在侧面BCC1B1中，∠EB1F不可能是直角.

若存在点E，使得EF⊥A1F，因为EF⊥A1B1，则EF⊥平面A1B1F，此时只需EF⊥FB1，①是正确命题.

若存在点E，使得B1E⊥A1F，因为B1E⊥A1B1，则B1E平面A1B1F，此时需∠EB1F是直角，这是不可能的，因此②是正确命题.

当点E为BC中点时，若∠B1EF是直角，则B1E⊥EF，■·■=（■+■）·（■+■）=■-2■=0，■=■，满足条件的点F有1个;若∠B1FE是直角，则B1F⊥EF，■·■=（■+■）·（■+■）=■+2■-■2 =0，■=1+■，满足条件的点F有0个. 因此，③是假命题.

当点F为CC1中点时，若∠B1EF是直角，则B1E⊥EF，■·■=（■+■）·（■+■）=3■-■2-2=0，■=1或■=2，满足条件的点E有2个;若∠B1FE是直角，则则B1F⊥EF，■·■=（■+■）·（■+■）=3■-1=0，■=■，满足条件的点E有1个. 因此，④是真命题.

四面体A1B1EF四个面所在平面，因为A1B1⊥平面B1EF，所以平面A1B1E⊥平面B1EF，平面A1B1F⊥平面B1EF;另外，若EF⊥平面A1B1F，还有平面A1B1F⊥平面A1EF（同理，若EF⊥平面A1B1E，还有平面A1B1E⊥平面A1EF）;因此仅有3对相互垂直.

故填①②④.

7. 利用体积为定值作球的截面圆（或点圆）

例12. 在三棱锥P-ABC中，AB=2，AC⊥BC，若三棱锥P-ABC的体积为■，则其外接球表面积的最小值为（）

A. 5？仔B. ■？仔C. ■？仔D. ■？仔

解析：如图所示，设∠ABC=？琢，则AC=2sin？琢，BC=2cos？琢，点P到底面ABC的距离为h，则VP-ABC=■hsin2？琢=■，h=■，点P在到底面ABC的距离为■的截面圆上（可以是点圆），设AB的中点为O1，外接球的球心为O，则外接球的半径R=■=■，显然h=■≥2（当且仅当？琢=45°时取得最小值，此时△ABC是等腰直角三角形），当h最小时OO1最小，也就是R最小. 此时OO1=2-R，解R=■可得R=■，其外接球表面积的最小值为■？仔，选D.

综上，与交线与截面有关的空间中的动点（轨迹）问题，要注意熟记空间中的公理和基本定理（主要是线面平行垂直和面面平行垂直），结合平面到空间的区别联系，充分利用等价转化和类比思想突破这一难点.

责任编辑 徐国坚